16.7梯形课件（北京课改版八年级下）

课件14张PPT。梯 形 知识与技能：1.掌握梯形的有关概念和性质；
2.初步掌握通过添加辅助线解决梯形问题
的方法。教学目标过程与方法：1.经历操作、猜想、证明的探索过程，
感受研究问题的方法；
2.经历借助添加辅助线将梯形转化成三角
形和平行四边形的过程，体会将复杂问
题转化为简单问题,将未知转化为已知的
方法。情感与态度：1.培养和发展学生的推理能力，渗透图形
转化思想；
2.培养学生敢于探索、独立自主学习的精神。引导探究法教学重点梯形的性质证明及辅助线的添加方法教学难点梯形中辅助线的添加教学方法教学过程 一、实物引入梯形的概念　　　 　　 定义：
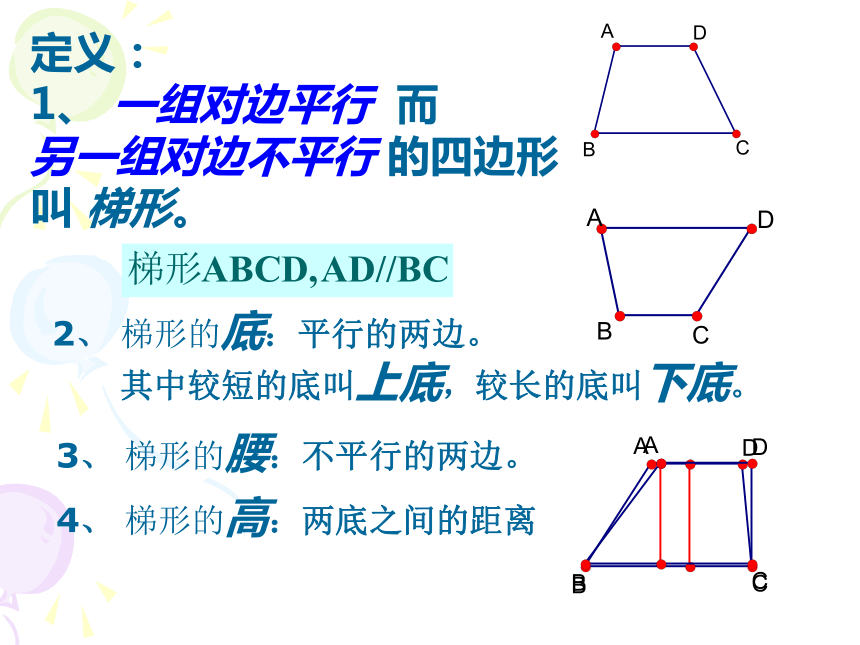
1、 一组对边平行 而
另一组对边不平行 的四边形
叫 梯形。2、 梯形的底：平行的两边。
其中较短的底叫上底，较长的底叫下底。 3、 梯形的腰：不平行的两边。 4、 梯形的高：两底之间的距离 想一想：
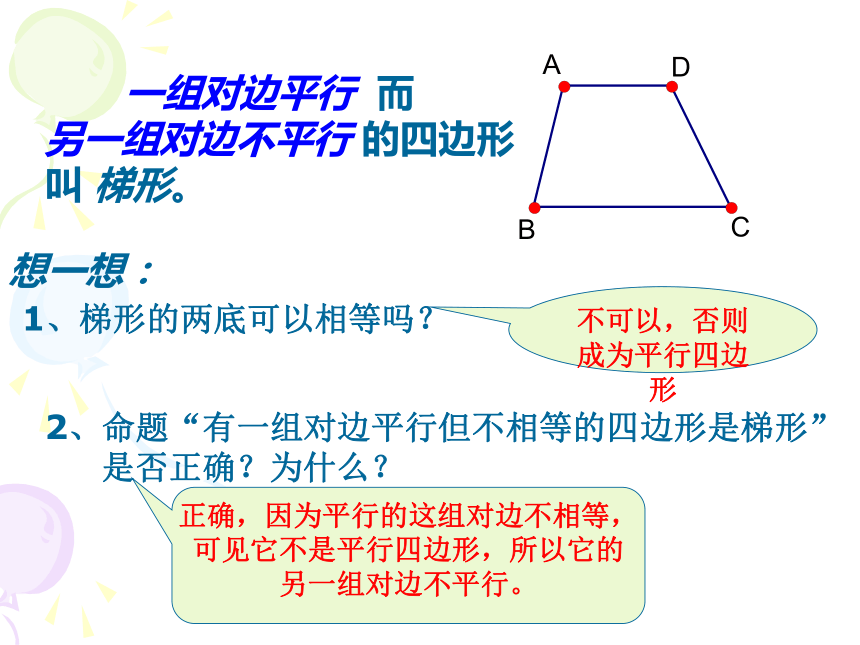
1、梯形的两底可以相等吗？ 2、命题“有一组对边平行但不相等的四边形是梯形”
是否正确？为什么？不可以，否则成为平行四边形正确，因为平行的这组对边不相等，可见它不是平行四边形，所以它的另一组对边不平行。 一组对边平行 而
另一组对边不平行 的四边形
叫 梯形。二、探索梯形的性质做一做：在你的横格本上做出一个梯形ABCD，
AD//BC，过腰AB的中点E作底AD
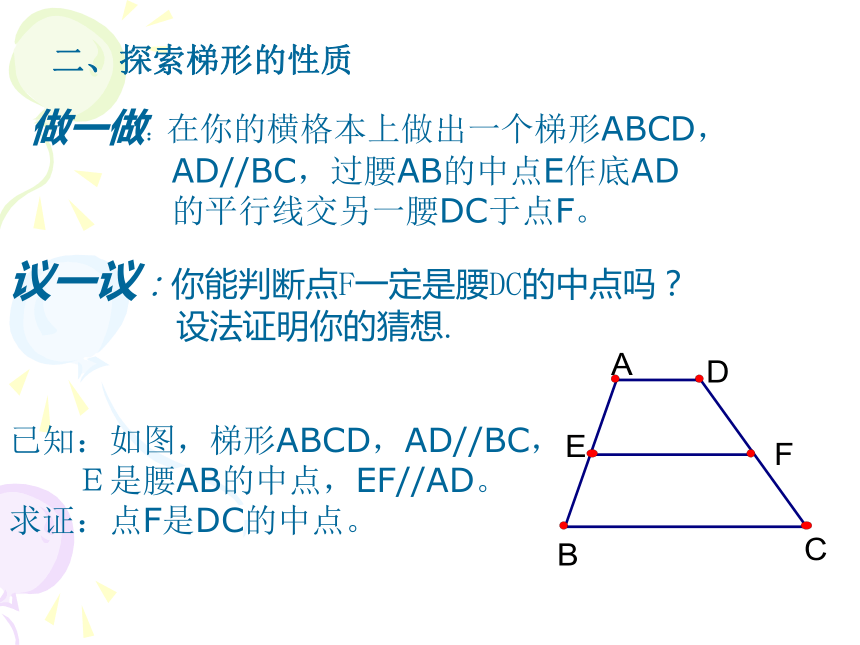
的平行线交另一腰DC于点F。议一议：你能判断点F一定是腰DC的中点吗？
设法证明你的猜想.已知：如图，梯形ABCD，AD//BC，
　　Ｅ是腰AB的中点，EF//AD。
求证：点F是DC的中点。 过点F作GH//AB，交BC于点G，交AD的延长线于点H 过点D作 DN//AB交EF于M， 交BC于点N证明：
则四边形AEMD和EBNM是平行四边形∴AE=DM，EB=MN ∵AE=EB ∴DM=MN 又∵EF//BC即 MF//BC ∴DF=FC （经过三角形一边的中点与另一边平行的直线平分第三边）
过点A、B、C、E作平行线能否证明此结论？
在研究梯形时，过点作平行线的目的是什么？二、探索梯形的性质符号表示：

梯形ABCD中，AD//BC
∵AE=EB， EF//AD
∴DF=FC（经过梯形一腰的中点与底边平行
的直线必平分另一腰）定理：经过梯形一腰的中点与底边平行
的直线，必平分另一腰。练习2、梯形的上底为4cm ，过上底的一个端点，
引一腰的平行线，与下底相交，所得三角形的
周长是12cm.求这个梯形的周长。例1 如图，梯形ABCD中，AD//BC，点E是AB的中点，FE//AD，分别交对角线AC，BD于G、H.
（1）图中可分解出几个“三角形中位线”这个基本图形？为什么？
（2）若AD=6，BC=10 ，求EG，GH，EF的长.
1 知识： ①梯形的概念（上下底，腰，对角线，高）
②定理 经过梯形一腰的中点与底边平行的
直线，必平分另一腰。
2 技能：添加辅助线将梯形转化成三角形和平行四边形
①借助中点构建全等三角形；
②过点作一腰的平行线，将梯形转化成三角形
和平行四边形；
在今后的学习中还会遇到其他的辅助线添加方法。
3 思想方法：“转化”的数学思想 三、课堂小结思考题： 已知：如图，梯形ABCD中，AD//BC，
AD=8cm, BC=17cm,∠C=80°,∠B=50°
求：CD的长。
方法一：过上底的一个顶点A作
腰CD的平行线，将腰CD
进行平移构成三角形。 方法二：延长两腰，
并相交构成三角形。 谢谢！