【沪科版八上同步练习】 第12章 一次函数(基础知识)检测题(含答案)
文档属性
| 名称 | 【沪科版八上同步练习】 第12章 一次函数(基础知识)检测题(含答案) | 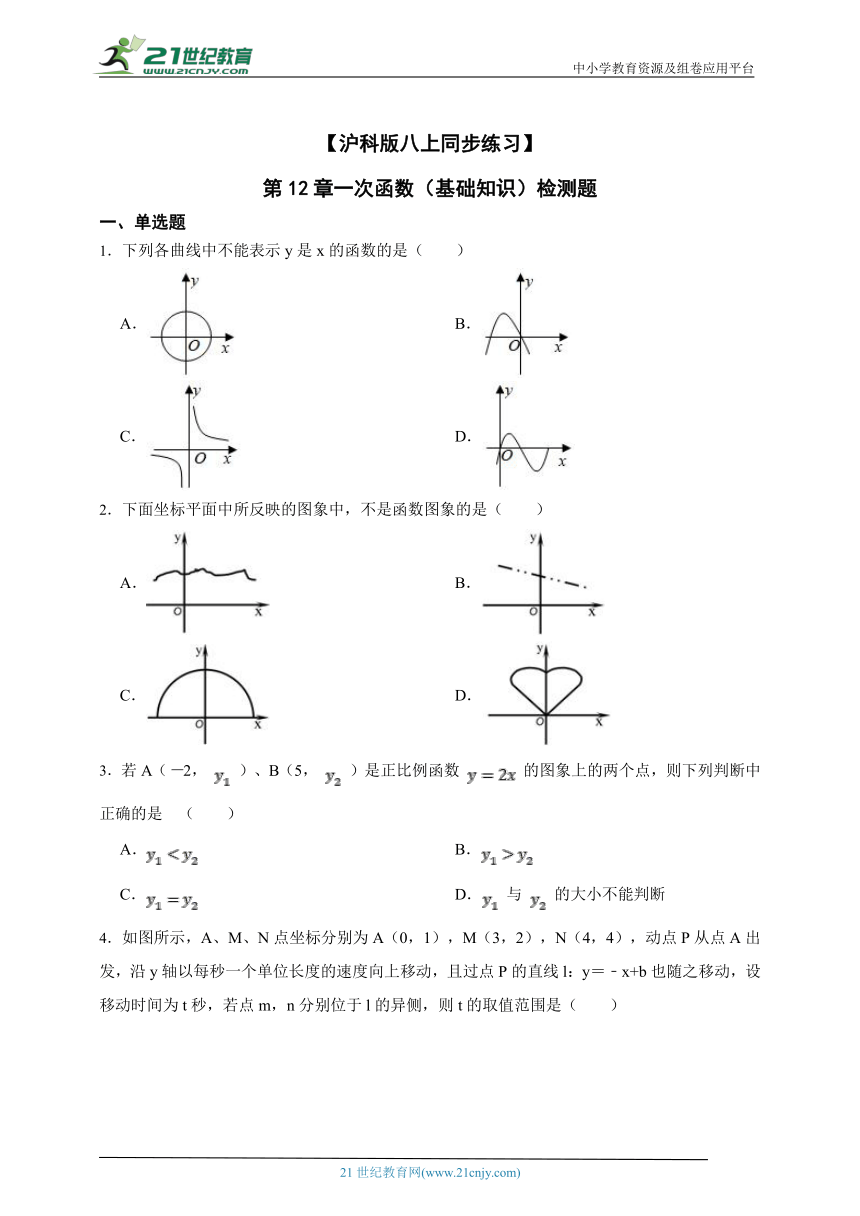 | |
| 格式 | doc | ||
| 文件大小 | 14.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-19 07:42:20 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【沪科版八上同步练习】
第12章一次函数(基础知识)检测题
一、单选题
1.下列各曲线中不能表示y是x的函数的是( )
A. B.
C. D.
2.下面坐标平面中所反映的图象中,不是函数图象的是( )
A. B.
C. D.
3.若A(-2, )、B(5, )是正比例函数 的图象上的两个点,则下列判断中正确的是 ( )
A. B.
C. D. 与 的大小不能判断
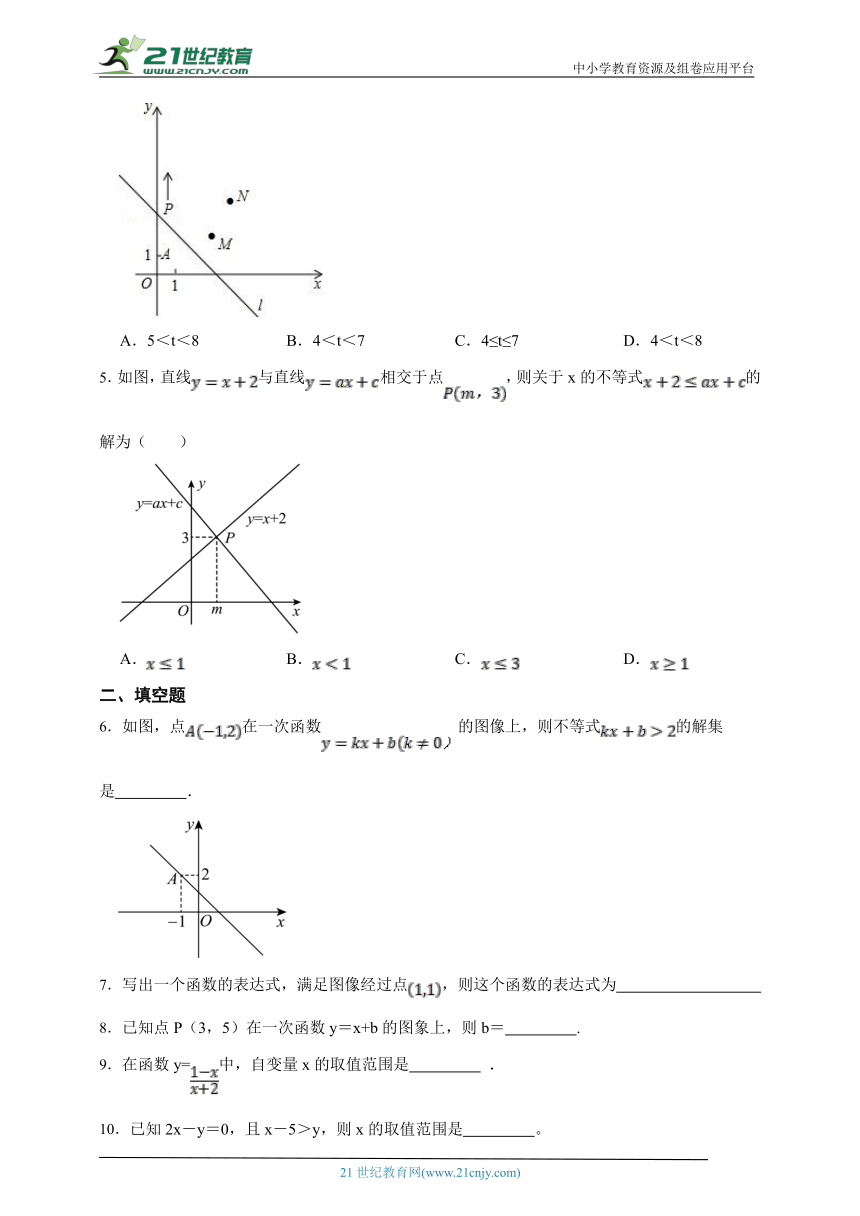
4.如图所示,A、M、N点坐标分别为A(0,1),M(3,2),N(4,4),动点P从点A出发,沿y轴以每秒一个单位长度的速度向上移动,且过点P的直线l:y=﹣x+b也随之移动,设移动时间为t秒,若点m,n分别位于l的异侧,则t的取值范围是( )
A.5<t<8 B.4<t<7 C.4≤t≤7 D.4<t<8
5.如图,直线与直线相交于点,则关于x的不等式的解为( )
A. B. C. D.
二、填空题
6.如图,点在一次函数的图像上,则不等式的解集是 .
7.写出一个函数的表达式,满足图像经过点,则这个函数的表达式为
8.已知点P(3,5)在一次函数y=x+b的图象上,则b= .
9.在函数y=中,自变量x的取值范围是 .
10.已知2x-y=0,且x-5>y,则x的取值范围是 。
11.如图,在平面直角坐标系中,直线y=﹣ x+3分别交y轴,x轴于A、B两点,点C在线段AB上,连接OC,且OC=BC.
(1)求线段AC的长度;
(2)如图2,点D的坐标为(﹣ ,0),过D作DE⊥BO交直线y=﹣ x+3于点E.动点N在x轴上从点D向终点O匀速运动,同时动点M在直线=﹣ x+3上从某一点向终点G(2 ,1)匀速运动,当点N运动到线段DO中点时,点M恰好与点A重合,且它们同时到达终点.
i)当点M在线段EG上时,设EM=s、DN=t,求s与t之间满足的一次函数关系式;
ii)在i)的基础上,连接MN,过点O作OF⊥AB于点F,当MN与△OFC的一边平行时,求所有满足条件的s的值.
三、计算题
12.已知函数.
(1)如果点在该函数的图象上,求的值;
(2)求出这个函数的图象与轴,轴的交点坐标.
13.已知一次函数 当 时, .
(1)求y与x之间的函数表达式;
(2)当 时,求x的值.
四、解答题
14.如图,直线与直线相交于点.
(1)求b,m的值;
(2)垂直于x轴的直线交直线于C,D两点,若线段CD长为6,求点D的坐标.
15.已知一次函数的图象经过,两点,并且与轴相交于点,求:和的值及点的坐标.
16.如图,在平面直角坐标系中,直线与x轴交于点,与y轴交于点,直线与x轴交于点C,与y轴交于点E,且与相交于D.点P为线段上一点(不与点D,E重合),作直线.
(1)求直线的表达式及点D的坐标;
(2)若直线将的面积分为两部分,求点P的坐标;
(3)点P是否存在某个位置,使得点D关于直线的对称点恰好落在直线上方的坐标轴上.若存在,直接写出点P的坐标;若不存在,请说明理由.
五、综合题
17.为丰富同学们的课余活动,某校成立了篮球课外兴趣小组,计划购买一批篮球,需购买 、 两种不同型号的篮球共300个.已知购买3个 型篮球和2个 型篮球共需340元,购买2个 型篮球和1个 型篮球共需要210元.
(1)求购买一个 型篮球、一个 型篮球各需多少元?
(2)若该校计划投入资金 元用于购买这两种篮球,设购进的 型篮球为 个,求 关于 的函数关系式;
(3)学校在体育用品专卖店购买 、 两种型号篮球共300个,经协商,专卖店给出如下优惠: 种球每个降价8元, 种球打9折,计算下来,学校共付费16740元,学校购买 、 两种篮球各多少个?
18.小丽的家和学校在一条笔直的马路旁,某天小丽沿着这条马路上学,先从家步行到公交站台甲,再乘车到公交站台乙下车,最后步行到学校(在整个过程中小丽步行的速度不变),图中折线ABCDE表示小丽和学校之间的距离y(米)与她离家时间x(分钟)之间的函数关系.
(1)求小丽步行的速度及学校与公交站台乙之间的距离;
(2)当8≤x≤15时,求y与x之间的函数关系式.
19.某天,甲车间工人加工零件,工作中有一次停产检修机器,然后以原来的工作效率继续加工,由于任务紧急,乙车间加入与甲车间一起生产零件,两组各自加工零件的数量y(个)与甲组加工时间t(时)之间的函数图象如图所示.
(1)求甲组加工零件总量a.
(2)求甲组加工零件的数量y与时间t之间的函数关系式,并写出t的取值范围.
(3)当甲、乙两车间加工零件总数量为300个时,直接写出t的值.
六、实践探究题
20.小明观察到一个水龙头因损坏而不断地向外滴水,为探究其漏水造成的浪费情况,小明用一个带有刻度的量筒放在水龙头下面装水,每隔一分钟记录量筒中的总水量,但由于操作延误,开始计时的时候量筒中已经有少量水,因而得到如下表的一组数据:
时间(分钟) 1 2 3 4 5
总水量(毫升) 7 12 17 22 27
(1)探究:根据上表中的数据,请判断总水量与时间的符合怎样的函数关系?并求出关于的表达式;
(2)应用:
①请你估算小明在第20分钟测量时量筒的总水量是多少毫升?
②一个人一天大约饮用1500毫升水,请你估算这个水龙头一个月(按30天计)的漏水量可供一人饮用多少天.
答案解析部分
1.【答案】A
【知识点】函数的概念
2.【答案】D
【知识点】函数的图象
3.【答案】A
【知识点】正比例函数的图象和性质
4.【答案】B
【知识点】一次函数的图象;一次函数中的动态几何问题
5.【答案】A
【知识点】一次函数与不等式(组)的关系
6.【答案】
【知识点】一次函数与不等式(组)的关系
7.【答案】(答案不唯一)
【知识点】函数解析式
8.【答案】2
【知识点】一次函数的性质
9.【答案】x≠﹣2
【知识点】函数自变量的取值范围
10.【答案】x<-5
【知识点】一次函数与不等式(组)的关系
11.【答案】(1)A、B、C的坐标分别为:(0,3)、(3 ,0);
OC=BC,则点C是AB的中点,则点C的坐标为:( , );
故AC= AB= 6=3;
(2)点A、B、C的坐标分别为:(0,3)、(3 ,0)、( , );
点D、E、G的坐标分别为:(﹣ ,0)、(﹣ ,4)、(2 ,1);
i)设s、t的表达式为:s=kt+b,
当t=DN= 时,s=EM=EA=2,即点( ,2);
当t=OD= 时,s=EG=6,即点( ,6);
将点( ,2)和点( ,6)代入s=kt+b并解得:
函数的表达式为:y= t﹣2…①;
ii)直线AB的倾斜角∠ABO=α=30°,EB=8,BD=4 ,DE=4,EM=s、DN=t,
①当MN∥OC时,如图1,
则∠MNB=∠COB=∠CBO=α=30°,
MN=BM=BE﹣EM=8﹣s,
NH= BN= (BD﹣DN)= (4 ﹣t),
cos∠MNH= = …②;
联立①②并解得:s= ;
②当MN∥OF时,如图2,
故点M作MG⊥ED角ED于点G,作NH⊥AG于点H,作AR⊥ED于点R,
则∠HNM=∠RAE=∠EBD=α=30°,
HN=GD=ED﹣EG=4﹣EMcos30°=4﹣ s,
MH=MG﹣GH=MEcos30°﹣t= s﹣t,
tanα= = …③;
联立①③并解得:s= ;
从图象看MN不可能平行于BC;
综上,s= 或 .
【知识点】一次函数图象与坐标轴交点问题;一次函数中的动态几何问题
12.【答案】(1)
(2)这个函数的图象与轴的交点为,与轴的交点为
【知识点】一次函数的概念;一次函数图象与坐标轴交点问题
13.【答案】(1)解:把 , 代入得: ,
解得: ,
则 ;
(2)解:把 代入得: ,
解得: .
【知识点】待定系数法求一次函数解析式
14.【答案】(1)解:将代入中,得,则,
将代入中,得,则;
(2)解:由(1)知,直线,
根据题意,设,,
∵,
∴,即,
∴或,
解得或,
∴点D的坐标为或.
【知识点】两一次函数图象相交或平行问题
15.【答案】解:一次函数的图象经过,
,
解得;
,
当时,,
点的坐标为.
【知识点】待定系数法求一次函数解析式;一次函数图象与坐标轴交点问题
16.【答案】(1);
(2)存在,或.
(3)存在.点P的坐标是或.
【知识点】待定系数法求一次函数解析式;一次函数与二元一次方程(组)的关系
17.【答案】(1)解:设一个A型篮球为x元,一个B型篮球为y元,根据题意可得:
,
解得: ,
∴一个A型篮球为80元,一个B型篮球为50元;
(2)解:A型篮球t个,则B型篮球为 个,根据题意可得:
,
∴函数解析式为: ;
(3)解:根据题意可得:A型篮球单价为 元,B型篮球单价为 元,则
,
解得: , ,
∴A型篮球120个,则B型篮球为180个.
【知识点】一次函数的实际应用;一元一次方程的实际应用-销售问题;二元一次方程组的实际应用-销售问题
18.【答案】(1)解:根据题意得:
小丽步行的速度为:(3900﹣3650)÷5=50(米/分钟),
学校与公交站台乙之间的距离为:(18﹣15)×50=150(米)
(2)解:当8≤x≤15时,设y=kx+b,
把C(8,3650),D(15,150)代入得: ,
解得:
∴y=﹣500x+7650(8≤x≤15)
【知识点】待定系数法求一次函数解析式;一次函数的实际应用
19.【答案】(1)解:∵甲车间的效率不变,在前三分钟内生产了120个,
∴甲车间的效率为每小时120÷3=40(个),
∴甲车间的生产总量为a=120+(8-4)×40=280(个);
(2)解:当时,
当时,
当时,
∴甲组加工零件的数量y与时间t之间的函数关系式为
(3)
【知识点】一次函数的实际应用
20.【答案】(1)解:根据上表中的数据,随着的增大而匀速增大,符合一次函数关系,
故可设(k,b为常数).
当时,,当时,,
.
解得.
;
(2)解:①当时,,
即估算小明在第20分钟测量时量筒的总水量是102毫升;
②当分钟时,(毫升),
当时,,
水龙头一个月(按30天计)的漏水量为:(毫升),
(天),
答:估算这个水龙头一个月(按30天计)的漏水量可供一人饮用144天.
【知识点】一次函数的实际应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【沪科版八上同步练习】
第12章一次函数(基础知识)检测题
一、单选题
1.下列各曲线中不能表示y是x的函数的是( )
A. B.
C. D.
2.下面坐标平面中所反映的图象中,不是函数图象的是( )
A. B.
C. D.
3.若A(-2, )、B(5, )是正比例函数 的图象上的两个点,则下列判断中正确的是 ( )
A. B.
C. D. 与 的大小不能判断
4.如图所示,A、M、N点坐标分别为A(0,1),M(3,2),N(4,4),动点P从点A出发,沿y轴以每秒一个单位长度的速度向上移动,且过点P的直线l:y=﹣x+b也随之移动,设移动时间为t秒,若点m,n分别位于l的异侧,则t的取值范围是( )
A.5<t<8 B.4<t<7 C.4≤t≤7 D.4<t<8
5.如图,直线与直线相交于点,则关于x的不等式的解为( )
A. B. C. D.
二、填空题
6.如图,点在一次函数的图像上,则不等式的解集是 .
7.写出一个函数的表达式,满足图像经过点,则这个函数的表达式为
8.已知点P(3,5)在一次函数y=x+b的图象上,则b= .
9.在函数y=中,自变量x的取值范围是 .
10.已知2x-y=0,且x-5>y,则x的取值范围是 。
11.如图,在平面直角坐标系中,直线y=﹣ x+3分别交y轴,x轴于A、B两点,点C在线段AB上,连接OC,且OC=BC.
(1)求线段AC的长度;
(2)如图2,点D的坐标为(﹣ ,0),过D作DE⊥BO交直线y=﹣ x+3于点E.动点N在x轴上从点D向终点O匀速运动,同时动点M在直线=﹣ x+3上从某一点向终点G(2 ,1)匀速运动,当点N运动到线段DO中点时,点M恰好与点A重合,且它们同时到达终点.
i)当点M在线段EG上时,设EM=s、DN=t,求s与t之间满足的一次函数关系式;
ii)在i)的基础上,连接MN,过点O作OF⊥AB于点F,当MN与△OFC的一边平行时,求所有满足条件的s的值.
三、计算题
12.已知函数.
(1)如果点在该函数的图象上,求的值;
(2)求出这个函数的图象与轴,轴的交点坐标.
13.已知一次函数 当 时, .
(1)求y与x之间的函数表达式;
(2)当 时,求x的值.
四、解答题
14.如图,直线与直线相交于点.
(1)求b,m的值;
(2)垂直于x轴的直线交直线于C,D两点,若线段CD长为6,求点D的坐标.
15.已知一次函数的图象经过,两点,并且与轴相交于点,求:和的值及点的坐标.
16.如图,在平面直角坐标系中,直线与x轴交于点,与y轴交于点,直线与x轴交于点C,与y轴交于点E,且与相交于D.点P为线段上一点(不与点D,E重合),作直线.
(1)求直线的表达式及点D的坐标;
(2)若直线将的面积分为两部分,求点P的坐标;
(3)点P是否存在某个位置,使得点D关于直线的对称点恰好落在直线上方的坐标轴上.若存在,直接写出点P的坐标;若不存在,请说明理由.
五、综合题
17.为丰富同学们的课余活动,某校成立了篮球课外兴趣小组,计划购买一批篮球,需购买 、 两种不同型号的篮球共300个.已知购买3个 型篮球和2个 型篮球共需340元,购买2个 型篮球和1个 型篮球共需要210元.
(1)求购买一个 型篮球、一个 型篮球各需多少元?
(2)若该校计划投入资金 元用于购买这两种篮球,设购进的 型篮球为 个,求 关于 的函数关系式;
(3)学校在体育用品专卖店购买 、 两种型号篮球共300个,经协商,专卖店给出如下优惠: 种球每个降价8元, 种球打9折,计算下来,学校共付费16740元,学校购买 、 两种篮球各多少个?
18.小丽的家和学校在一条笔直的马路旁,某天小丽沿着这条马路上学,先从家步行到公交站台甲,再乘车到公交站台乙下车,最后步行到学校(在整个过程中小丽步行的速度不变),图中折线ABCDE表示小丽和学校之间的距离y(米)与她离家时间x(分钟)之间的函数关系.
(1)求小丽步行的速度及学校与公交站台乙之间的距离;
(2)当8≤x≤15时,求y与x之间的函数关系式.
19.某天,甲车间工人加工零件,工作中有一次停产检修机器,然后以原来的工作效率继续加工,由于任务紧急,乙车间加入与甲车间一起生产零件,两组各自加工零件的数量y(个)与甲组加工时间t(时)之间的函数图象如图所示.
(1)求甲组加工零件总量a.
(2)求甲组加工零件的数量y与时间t之间的函数关系式,并写出t的取值范围.
(3)当甲、乙两车间加工零件总数量为300个时,直接写出t的值.
六、实践探究题
20.小明观察到一个水龙头因损坏而不断地向外滴水,为探究其漏水造成的浪费情况,小明用一个带有刻度的量筒放在水龙头下面装水,每隔一分钟记录量筒中的总水量,但由于操作延误,开始计时的时候量筒中已经有少量水,因而得到如下表的一组数据:
时间(分钟) 1 2 3 4 5
总水量(毫升) 7 12 17 22 27
(1)探究:根据上表中的数据,请判断总水量与时间的符合怎样的函数关系?并求出关于的表达式;
(2)应用:
①请你估算小明在第20分钟测量时量筒的总水量是多少毫升?
②一个人一天大约饮用1500毫升水,请你估算这个水龙头一个月(按30天计)的漏水量可供一人饮用多少天.
答案解析部分
1.【答案】A
【知识点】函数的概念
2.【答案】D
【知识点】函数的图象
3.【答案】A
【知识点】正比例函数的图象和性质
4.【答案】B
【知识点】一次函数的图象;一次函数中的动态几何问题
5.【答案】A
【知识点】一次函数与不等式(组)的关系
6.【答案】
【知识点】一次函数与不等式(组)的关系
7.【答案】(答案不唯一)
【知识点】函数解析式
8.【答案】2
【知识点】一次函数的性质
9.【答案】x≠﹣2
【知识点】函数自变量的取值范围
10.【答案】x<-5
【知识点】一次函数与不等式(组)的关系
11.【答案】(1)A、B、C的坐标分别为:(0,3)、(3 ,0);
OC=BC,则点C是AB的中点,则点C的坐标为:( , );
故AC= AB= 6=3;
(2)点A、B、C的坐标分别为:(0,3)、(3 ,0)、( , );
点D、E、G的坐标分别为:(﹣ ,0)、(﹣ ,4)、(2 ,1);
i)设s、t的表达式为:s=kt+b,
当t=DN= 时,s=EM=EA=2,即点( ,2);
当t=OD= 时,s=EG=6,即点( ,6);
将点( ,2)和点( ,6)代入s=kt+b并解得:
函数的表达式为:y= t﹣2…①;
ii)直线AB的倾斜角∠ABO=α=30°,EB=8,BD=4 ,DE=4,EM=s、DN=t,
①当MN∥OC时,如图1,
则∠MNB=∠COB=∠CBO=α=30°,
MN=BM=BE﹣EM=8﹣s,
NH= BN= (BD﹣DN)= (4 ﹣t),
cos∠MNH= = …②;
联立①②并解得:s= ;
②当MN∥OF时,如图2,
故点M作MG⊥ED角ED于点G,作NH⊥AG于点H,作AR⊥ED于点R,
则∠HNM=∠RAE=∠EBD=α=30°,
HN=GD=ED﹣EG=4﹣EMcos30°=4﹣ s,
MH=MG﹣GH=MEcos30°﹣t= s﹣t,
tanα= = …③;
联立①③并解得:s= ;
从图象看MN不可能平行于BC;
综上,s= 或 .
【知识点】一次函数图象与坐标轴交点问题;一次函数中的动态几何问题
12.【答案】(1)
(2)这个函数的图象与轴的交点为,与轴的交点为
【知识点】一次函数的概念;一次函数图象与坐标轴交点问题
13.【答案】(1)解:把 , 代入得: ,
解得: ,
则 ;
(2)解:把 代入得: ,
解得: .
【知识点】待定系数法求一次函数解析式
14.【答案】(1)解:将代入中,得,则,
将代入中,得,则;
(2)解:由(1)知,直线,
根据题意,设,,
∵,
∴,即,
∴或,
解得或,
∴点D的坐标为或.
【知识点】两一次函数图象相交或平行问题
15.【答案】解:一次函数的图象经过,
,
解得;
,
当时,,
点的坐标为.
【知识点】待定系数法求一次函数解析式;一次函数图象与坐标轴交点问题
16.【答案】(1);
(2)存在,或.
(3)存在.点P的坐标是或.
【知识点】待定系数法求一次函数解析式;一次函数与二元一次方程(组)的关系
17.【答案】(1)解:设一个A型篮球为x元,一个B型篮球为y元,根据题意可得:
,
解得: ,
∴一个A型篮球为80元,一个B型篮球为50元;
(2)解:A型篮球t个,则B型篮球为 个,根据题意可得:
,
∴函数解析式为: ;
(3)解:根据题意可得:A型篮球单价为 元,B型篮球单价为 元,则
,
解得: , ,
∴A型篮球120个,则B型篮球为180个.
【知识点】一次函数的实际应用;一元一次方程的实际应用-销售问题;二元一次方程组的实际应用-销售问题
18.【答案】(1)解:根据题意得:
小丽步行的速度为:(3900﹣3650)÷5=50(米/分钟),
学校与公交站台乙之间的距离为:(18﹣15)×50=150(米)
(2)解:当8≤x≤15时,设y=kx+b,
把C(8,3650),D(15,150)代入得: ,
解得:
∴y=﹣500x+7650(8≤x≤15)
【知识点】待定系数法求一次函数解析式;一次函数的实际应用
19.【答案】(1)解:∵甲车间的效率不变,在前三分钟内生产了120个,
∴甲车间的效率为每小时120÷3=40(个),
∴甲车间的生产总量为a=120+(8-4)×40=280(个);
(2)解:当时,
当时,
当时,
∴甲组加工零件的数量y与时间t之间的函数关系式为
(3)
【知识点】一次函数的实际应用
20.【答案】(1)解:根据上表中的数据,随着的增大而匀速增大,符合一次函数关系,
故可设(k,b为常数).
当时,,当时,,
.
解得.
;
(2)解:①当时,,
即估算小明在第20分钟测量时量筒的总水量是102毫升;
②当分钟时,(毫升),
当时,,
水龙头一个月(按30天计)的漏水量为:(毫升),
(天),
答:估算这个水龙头一个月(按30天计)的漏水量可供一人饮用144天.
【知识点】一次函数的实际应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
