【沪科版八上同步练习】 第12章 一次函数(能力提升)检测题(含答案)
文档属性
| 名称 | 【沪科版八上同步练习】 第12章 一次函数(能力提升)检测题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 11.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-19 07:43:26 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【沪科版八上同步练习】
第12章一次函数(能力提升)检测题
一、填空题
1.函数的表示方法有三种,分别是 、 、 。
2.在变量x与y的关系式中,当自变量时,因变量y的值为 .
3.若函数的图象经过点,其图像如图所示,则关于x的不等式的解集为 .
4.如图,直线y=kx+b与y= x交于A(3,1)与x轴交于B(6,0),则不等式组0 的解集为 .
5.将一次函数y=3x﹣1的图象沿y轴向 平移 个单位后,得到的图象经过原点.
6.已知一次函数:y1=2x+1,y2=ax-a(a为常数),当x>0时,y1>y2,则a的取值范围是 .
二、单选题
7.若一次函数 的函数值 随 的增大而增大,则( )
A. B. C. D.
8.下列四个函数中,一次函数是( )
A.y=x2﹣2x B.y=x﹣2 C. D.y=+1
9.小明在平面直角坐标系内画了一个一次函数的图象,图象特点如下:①图象过点;②图象与轴的交点在轴下方;③随的增大而增大.符合该图象特点的函数关系式为( )
A. B. C. D.
10.对于函数,下列结论错误的是( )
A.函数图象必经过点(1,3) B.y的值随x值的增大而增大
C.当时, D.函数图象经过第三象限
11.如图,直线y1=k1x+a与y2=k2x+b的交点坐标为(1,2),则使y1<y2的x的取值范围为( )
A.x>1 B.x>2 C.x<1 D.x<2
三、解答题
12.已知一次函数:,其中.
(1)若一次函数:的图象过点,求当时,的取值范围;
(2)若对于一次函数:,其中,若对任意实数,总有,求的取值范围.
13.已知函数
(1)若函数图象经过原点,求的值;
(2)若函数的图象平行于直线,求的值.
14.如图,直角坐标系中,一次函数的图象分别与x,y轴交于A,B两点,正比例函数的图象与交于点.
(1)求m的值及的解析式;
(2)求的值;
(3)一次函数的图象为,且,,不能围成三角形,直接写出k的值.
四、计算题
15.已知.
(1)化简P;
(2)若点在一次函数的图象上,求Р的值.
16.已知一次函数y=kx+b的图像经过点(-2,-4),且与正比例函数 的图像相交于点(4,a ),求:
(1)a的值;
(2)k、b的值
五、综合题
17.某中学要在校园内划出一块面积是100m2的长方形形土地做花圃,设这个矩形的相邻两边的长分别为xm和ym.
(1)求y关于x的函数解析式;
(2)说明当x=10时的实际意义.
18.某公司市场营销部的营销员的个人月收入y(元)与该营销员每月的销售量x(万件)成一次函数关系,图象如图所示.根据图象提供的信息,解答下列问题:
(1)求出营销员的个人月收入y(元)与该营销员每月的销售量x(万件)( )之间的函数关系式.
(2)该公司营销员李平5月份的销货量为 万件,求李平5月份收入.
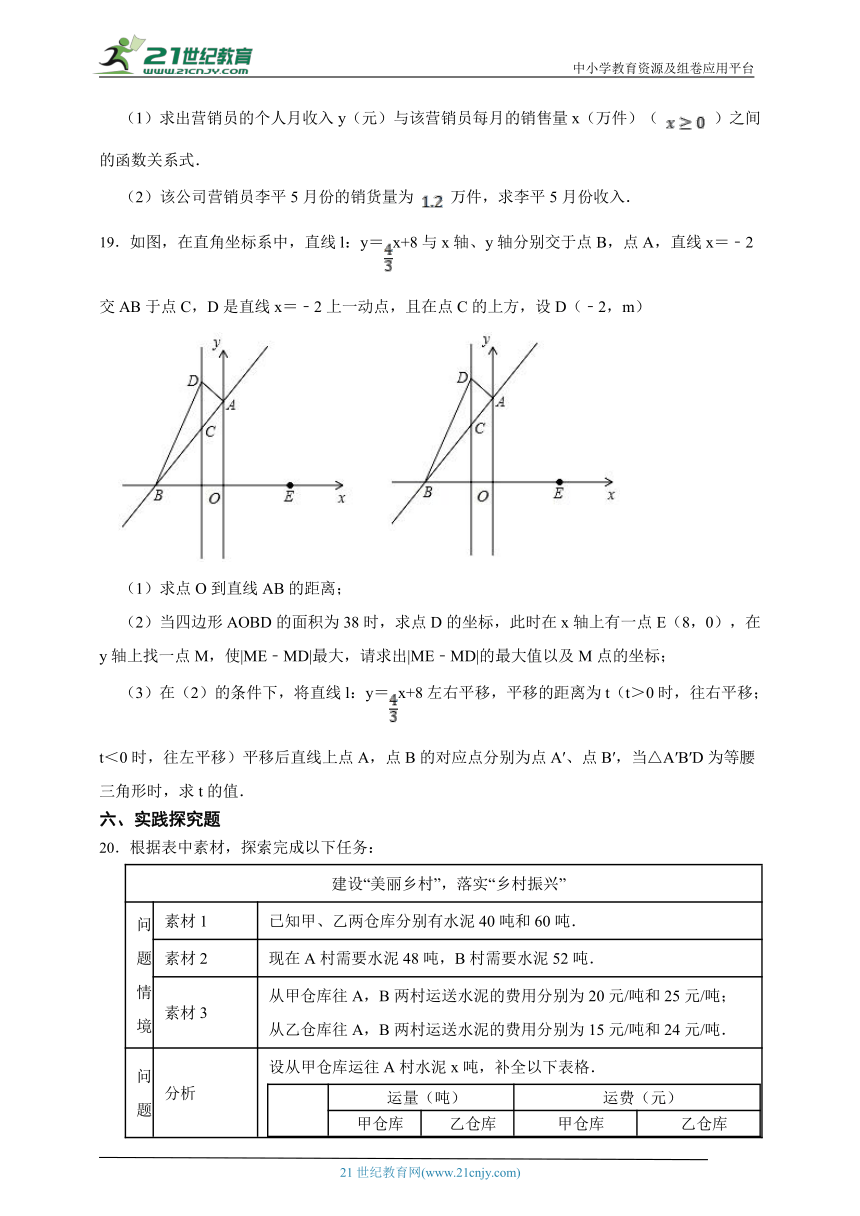
19.如图,在直角坐标系中,直线l:y=x+8与x轴、y轴分别交于点B,点A,直线x=﹣2交AB于点C,D是直线x=﹣2上一动点,且在点C的上方,设D(﹣2,m)
(1)求点O到直线AB的距离;
(2)当四边形AOBD的面积为38时,求点D的坐标,此时在x轴上有一点E(8,0),在y轴上找一点M,使|ME﹣MD|最大,请求出|ME﹣MD|的最大值以及M点的坐标;
(3)在(2)的条件下,将直线l:y=x+8左右平移,平移的距离为t(t>0时,往右平移;t<0时,往左平移)平移后直线上点A,点B的对应点分别为点A′、点B′,当△A′B′D为等腰三角形时,求t的值.
六、实践探究题
20.根据表中素材,探索完成以下任务:
建设“美丽乡村”,落实“乡村振兴”
问题情境 素材1 已知甲、乙两仓库分别有水泥40吨和60吨.
素材2 现在A村需要水泥48吨,B村需要水泥52吨.
素材3 从甲仓库往A,B两村运送水泥的费用分别为20元/吨和25元/吨;从乙仓库往A,B两村运送水泥的费用分别为15元/吨和24元/吨.
问题解决 分析 设从甲仓库运往A村水泥x吨,补全以下表格. 运量(吨)运费(元)甲仓库乙仓库甲仓库乙仓库A村xB村① ▲ ② ▲
问题1 设总运费为y元,请写出y与x的函数关系式并求出最少总运费.
问题2 为了更好地支援乡村建设,甲仓库运往A村的运费每吨减少元,这时甲仓库运往A村的水泥多少吨时总运费最少?最少费用为多少元?(用含a的代数式表示)
答案解析部分
1.【答案】列表法;关系式法;图象法
【知识点】函数的表示方法
2.【答案】2
【知识点】函数值
3.【答案】x<0
【知识点】一次函数与不等式(组)的关系
4.【答案】3<x<6
【知识点】一次函数与不等式(组)的关系
5.【答案】上;1
【知识点】一次函数图象与几何变换
6.【答案】-1≤a<0或0<a≤2
【知识点】一次函数与不等式(组)的关系
7.【答案】B
【知识点】一次函数的性质
8.【答案】B
【知识点】一次函数的概念
9.【答案】D
【知识点】一次函数的概念;一次函数的性质
10.【答案】C
【知识点】正比例函数的图象和性质
11.【答案】C
【知识点】两一次函数图象相交或平行问题
12.【答案】(1)
(2)
【知识点】待定系数法求一次函数解析式;一次函数与不等式(组)的关系
13.【答案】(1)解:
(2)解:
【知识点】两一次函数图象相交或平行问题;一次函数的性质
14.【答案】(1)解:把代入一次函数,可得,解得,
,
设的解析式为,则,解得,
的解析式为
(2)解:如图,过作于,于,则,,
,令,则;令,则,
,,,,
(3)解:一次函数的图象为,且,,不能围成三角形,
当经过点时,;当,平行时,;当,平行时,;
故的值为或2或.
【知识点】待定系数法求一次函数解析式;一次函数与二元一次方程(组)的关系
15.【答案】(1)
(2)
【知识点】分式的化简求值;一次函数的概念
16.【答案】(1)解:∵ 在正比例函数 图象上,
∴将 代入 ,得 ;
(2)解:由(1)知一次函数 经过点 和 ,
列式 ,解得 .
【知识点】正比例函数的图象和性质;待定系数法求一次函数解析式
17.【答案】(1)解:根据矩形面积公式可得xy=100,
故
(2)解:把x=10代入 中得y=10.
实际意义:这是一个正方形
【知识点】函数解析式;函数值
18.【答案】(1)解:设所求的函数关系式为 ,
函数图象过 和 两点,
,解得 ,
即营销员的个人月收入y(元)与该营销员每月的销售量x(万件)( )之间的函数关系式为 .
(2)解:当 时, ,
即李平5月份的收入为2000元.
【知识点】待定系数法求一次函数解析式;一次函数的实际应用
19.【答案】(1)解:当x=0时,y=x+8=8,
∴A(0,8),
∴OA=8;
当y=x+8=0时,y=﹣6,
∴B(﹣6,0),
∴OB=6.
∴AB==10,
∴点O到直线AB的距离==4.8.
(2)解:当x=﹣2时,y=x+8=,
∴C(﹣2,),
∴S四边形AOBD=S△ABD+S△AOB=CD (xA﹣xB)+OA OB=3m+8=38,
解得:m=10,
∴当四边形AOBD的面积为38时,点D的坐标为(﹣2,10).
在x轴负半轴上找出点E关于y轴对称的点E′(﹣8,0),连接E′D并延长交y轴于点M,连接DM,此时|ME﹣MD|最大,最大值为线段DE′的长度,如图1所示.
DE′=.
设直线DE′的解析式为y=kx+b(k≠0),
将D(﹣2,10)、E′(﹣8,0)代入y=kx+b,
,解得:,
∴直线DE′的解析式为y=x+,
∴点M的坐标为(0,).
故当点M的坐标为(0,)时,|ME﹣MD|取最大值2.
(3)解:∵A(0,8),B(﹣6,0),
∴点A′的坐标为(t,8),点B′的坐标为(t﹣6,0),
∵点D(﹣2,10),
∴B′D==,A′B′==10,A′D==.
△A′B′D为等腰三角形分三种情况:
①当B′D=A′D时,有=,
解得:t=9;
②当B′D=A′B′时,有=10,
解得:t=4;
③当A′B′=A′D时,有10=,
解得:t1=﹣2﹣4(舍去),t2=﹣2+4.
综上所述:当△A′B′D为等腰三角形时,t的值为﹣2﹣4、4、﹣2+4或9.
【知识点】待定系数法求一次函数解析式;点到直线的距离;一次函数中的动态几何问题
20.【答案】解:分析:12+x;24(12+x);
问题1:
∵k=4>0,y随x的增大而增大,
∴当时,有最小值, .
问题2:由题意得,设新的总运费为W,
则
,
随着x的增大而减小,
∴当时,有最小值,.
【知识点】一次函数的实际应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【沪科版八上同步练习】
第12章一次函数(能力提升)检测题
一、填空题
1.函数的表示方法有三种,分别是 、 、 。
2.在变量x与y的关系式中,当自变量时,因变量y的值为 .
3.若函数的图象经过点,其图像如图所示,则关于x的不等式的解集为 .
4.如图,直线y=kx+b与y= x交于A(3,1)与x轴交于B(6,0),则不等式组0 的解集为 .
5.将一次函数y=3x﹣1的图象沿y轴向 平移 个单位后,得到的图象经过原点.
6.已知一次函数:y1=2x+1,y2=ax-a(a为常数),当x>0时,y1>y2,则a的取值范围是 .
二、单选题
7.若一次函数 的函数值 随 的增大而增大,则( )
A. B. C. D.
8.下列四个函数中,一次函数是( )
A.y=x2﹣2x B.y=x﹣2 C. D.y=+1
9.小明在平面直角坐标系内画了一个一次函数的图象,图象特点如下:①图象过点;②图象与轴的交点在轴下方;③随的增大而增大.符合该图象特点的函数关系式为( )
A. B. C. D.
10.对于函数,下列结论错误的是( )
A.函数图象必经过点(1,3) B.y的值随x值的增大而增大
C.当时, D.函数图象经过第三象限
11.如图,直线y1=k1x+a与y2=k2x+b的交点坐标为(1,2),则使y1<y2的x的取值范围为( )
A.x>1 B.x>2 C.x<1 D.x<2
三、解答题
12.已知一次函数:,其中.
(1)若一次函数:的图象过点,求当时,的取值范围;
(2)若对于一次函数:,其中,若对任意实数,总有,求的取值范围.
13.已知函数
(1)若函数图象经过原点,求的值;
(2)若函数的图象平行于直线,求的值.
14.如图,直角坐标系中,一次函数的图象分别与x,y轴交于A,B两点,正比例函数的图象与交于点.
(1)求m的值及的解析式;
(2)求的值;
(3)一次函数的图象为,且,,不能围成三角形,直接写出k的值.
四、计算题
15.已知.
(1)化简P;
(2)若点在一次函数的图象上,求Р的值.
16.已知一次函数y=kx+b的图像经过点(-2,-4),且与正比例函数 的图像相交于点(4,a ),求:
(1)a的值;
(2)k、b的值
五、综合题
17.某中学要在校园内划出一块面积是100m2的长方形形土地做花圃,设这个矩形的相邻两边的长分别为xm和ym.
(1)求y关于x的函数解析式;
(2)说明当x=10时的实际意义.
18.某公司市场营销部的营销员的个人月收入y(元)与该营销员每月的销售量x(万件)成一次函数关系,图象如图所示.根据图象提供的信息,解答下列问题:
(1)求出营销员的个人月收入y(元)与该营销员每月的销售量x(万件)( )之间的函数关系式.
(2)该公司营销员李平5月份的销货量为 万件,求李平5月份收入.
19.如图,在直角坐标系中,直线l:y=x+8与x轴、y轴分别交于点B,点A,直线x=﹣2交AB于点C,D是直线x=﹣2上一动点,且在点C的上方,设D(﹣2,m)
(1)求点O到直线AB的距离;
(2)当四边形AOBD的面积为38时,求点D的坐标,此时在x轴上有一点E(8,0),在y轴上找一点M,使|ME﹣MD|最大,请求出|ME﹣MD|的最大值以及M点的坐标;
(3)在(2)的条件下,将直线l:y=x+8左右平移,平移的距离为t(t>0时,往右平移;t<0时,往左平移)平移后直线上点A,点B的对应点分别为点A′、点B′,当△A′B′D为等腰三角形时,求t的值.
六、实践探究题
20.根据表中素材,探索完成以下任务:
建设“美丽乡村”,落实“乡村振兴”
问题情境 素材1 已知甲、乙两仓库分别有水泥40吨和60吨.
素材2 现在A村需要水泥48吨,B村需要水泥52吨.
素材3 从甲仓库往A,B两村运送水泥的费用分别为20元/吨和25元/吨;从乙仓库往A,B两村运送水泥的费用分别为15元/吨和24元/吨.
问题解决 分析 设从甲仓库运往A村水泥x吨,补全以下表格. 运量(吨)运费(元)甲仓库乙仓库甲仓库乙仓库A村xB村① ▲ ② ▲
问题1 设总运费为y元,请写出y与x的函数关系式并求出最少总运费.
问题2 为了更好地支援乡村建设,甲仓库运往A村的运费每吨减少元,这时甲仓库运往A村的水泥多少吨时总运费最少?最少费用为多少元?(用含a的代数式表示)
答案解析部分
1.【答案】列表法;关系式法;图象法
【知识点】函数的表示方法
2.【答案】2
【知识点】函数值
3.【答案】x<0
【知识点】一次函数与不等式(组)的关系
4.【答案】3<x<6
【知识点】一次函数与不等式(组)的关系
5.【答案】上;1
【知识点】一次函数图象与几何变换
6.【答案】-1≤a<0或0<a≤2
【知识点】一次函数与不等式(组)的关系
7.【答案】B
【知识点】一次函数的性质
8.【答案】B
【知识点】一次函数的概念
9.【答案】D
【知识点】一次函数的概念;一次函数的性质
10.【答案】C
【知识点】正比例函数的图象和性质
11.【答案】C
【知识点】两一次函数图象相交或平行问题
12.【答案】(1)
(2)
【知识点】待定系数法求一次函数解析式;一次函数与不等式(组)的关系
13.【答案】(1)解:
(2)解:
【知识点】两一次函数图象相交或平行问题;一次函数的性质
14.【答案】(1)解:把代入一次函数,可得,解得,
,
设的解析式为,则,解得,
的解析式为
(2)解:如图,过作于,于,则,,
,令,则;令,则,
,,,,
(3)解:一次函数的图象为,且,,不能围成三角形,
当经过点时,;当,平行时,;当,平行时,;
故的值为或2或.
【知识点】待定系数法求一次函数解析式;一次函数与二元一次方程(组)的关系
15.【答案】(1)
(2)
【知识点】分式的化简求值;一次函数的概念
16.【答案】(1)解:∵ 在正比例函数 图象上,
∴将 代入 ,得 ;
(2)解:由(1)知一次函数 经过点 和 ,
列式 ,解得 .
【知识点】正比例函数的图象和性质;待定系数法求一次函数解析式
17.【答案】(1)解:根据矩形面积公式可得xy=100,
故
(2)解:把x=10代入 中得y=10.
实际意义:这是一个正方形
【知识点】函数解析式;函数值
18.【答案】(1)解:设所求的函数关系式为 ,
函数图象过 和 两点,
,解得 ,
即营销员的个人月收入y(元)与该营销员每月的销售量x(万件)( )之间的函数关系式为 .
(2)解:当 时, ,
即李平5月份的收入为2000元.
【知识点】待定系数法求一次函数解析式;一次函数的实际应用
19.【答案】(1)解:当x=0时,y=x+8=8,
∴A(0,8),
∴OA=8;
当y=x+8=0时,y=﹣6,
∴B(﹣6,0),
∴OB=6.
∴AB==10,
∴点O到直线AB的距离==4.8.
(2)解:当x=﹣2时,y=x+8=,
∴C(﹣2,),
∴S四边形AOBD=S△ABD+S△AOB=CD (xA﹣xB)+OA OB=3m+8=38,
解得:m=10,
∴当四边形AOBD的面积为38时,点D的坐标为(﹣2,10).
在x轴负半轴上找出点E关于y轴对称的点E′(﹣8,0),连接E′D并延长交y轴于点M,连接DM,此时|ME﹣MD|最大,最大值为线段DE′的长度,如图1所示.
DE′=.
设直线DE′的解析式为y=kx+b(k≠0),
将D(﹣2,10)、E′(﹣8,0)代入y=kx+b,
,解得:,
∴直线DE′的解析式为y=x+,
∴点M的坐标为(0,).
故当点M的坐标为(0,)时,|ME﹣MD|取最大值2.
(3)解:∵A(0,8),B(﹣6,0),
∴点A′的坐标为(t,8),点B′的坐标为(t﹣6,0),
∵点D(﹣2,10),
∴B′D==,A′B′==10,A′D==.
△A′B′D为等腰三角形分三种情况:
①当B′D=A′D时,有=,
解得:t=9;
②当B′D=A′B′时,有=10,
解得:t=4;
③当A′B′=A′D时,有10=,
解得:t1=﹣2﹣4(舍去),t2=﹣2+4.
综上所述:当△A′B′D为等腰三角形时,t的值为﹣2﹣4、4、﹣2+4或9.
【知识点】待定系数法求一次函数解析式;点到直线的距离;一次函数中的动态几何问题
20.【答案】解:分析:12+x;24(12+x);
问题1:
∵k=4>0,y随x的增大而增大,
∴当时,有最小值, .
问题2:由题意得,设新的总运费为W,
则
,
随着x的增大而减小,
∴当时,有最小值,.
【知识点】一次函数的实际应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
