16.3.2平行四边形的判定课件(1)(北京课改版八年级下)
文档属性
| 名称 | 16.3.2平行四边形的判定课件(1)(北京课改版八年级下) |

|
|
| 格式 | rar | ||
| 文件大小 | 70.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-21 00:00:00 | ||
图片预览






文档简介
课件20张PPT。16.3.2平行四边形的判定(1)教学目标:知识与技能: 掌握平行四边形判定定理1、2,
并会运用判定定理解决相关问题。 教学目标:过程与方法: 1、经历对平行四边形判定方法的探究,使学生掌握并学会简单应用.
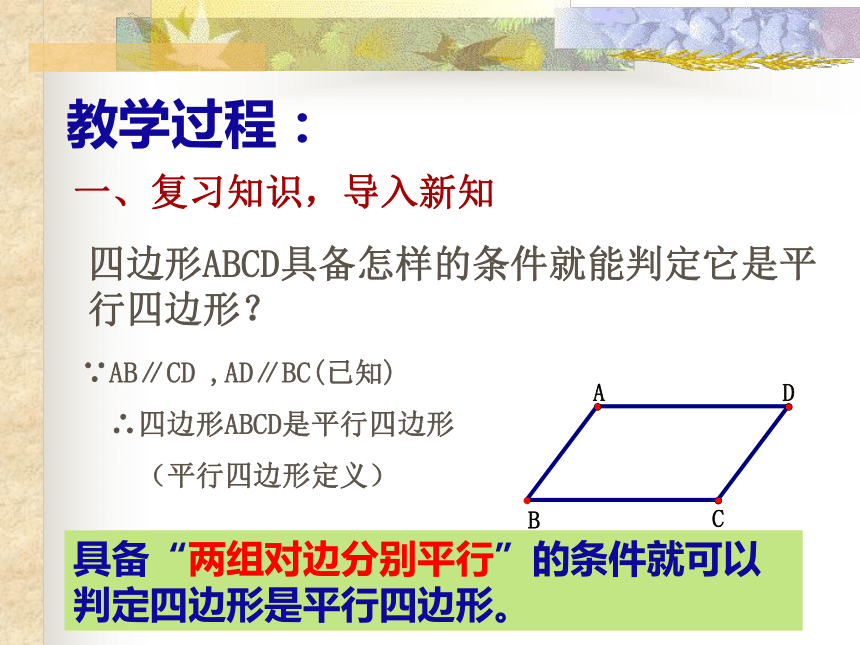
2、培养学生观察、分析、归纳的能力,养成勇于探索敢于创新的良好习惯,以及培养用数学方法分析、解决实际问题的能力,发展合情推理能力和说理能力。 教学目标:情感与态度: 学生通过观察、试验、类比、获得数学的猜想,体验数学活动充满着探索性和创造性,感受证明的必要性,证明过程的严谨性以及结论的准确性。发展学生克服困难的意志,通过一题多解激发学生的学习兴趣。 教学重点:掌握平行四边形的判定定理及其应用 教学难点:平行四边形判定定理的探究和归纳。 难点突破: 通过问题情境的设计,课堂实验研讨,引导学生发现、分析和解决问题。 教学方法: 合作探究式教学方法教学用具:多媒体辅助教学 教学过程:一、复习知识,导入新知 四边形ABCD具备怎样的条件就能判定它是平行四边形? ∵AB∥CD ,AD∥BC(已知)
∴四边形ABCD是平行四边形
(平行四边形定义) 具备“两组对边分别平行”的条件就可以判定四边形是平行四边形。 二、创设情景,探索新知 教学过程:探究活动:
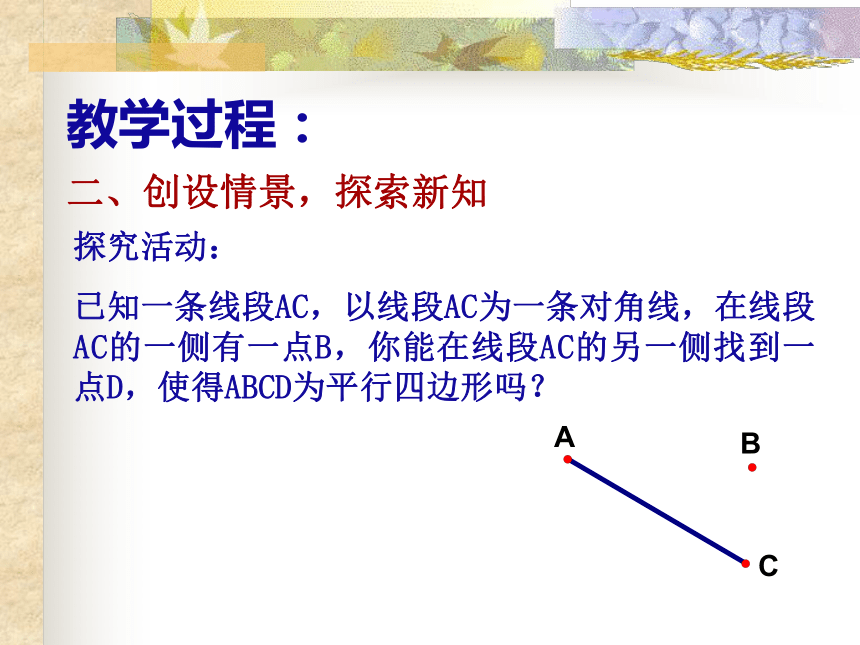
已知一条线段AC,以线段AC为一条对角线,在线段AC的一侧有一点B,你能在线段AC的另一侧找到一点D,使得ABCD为平行四边形吗?
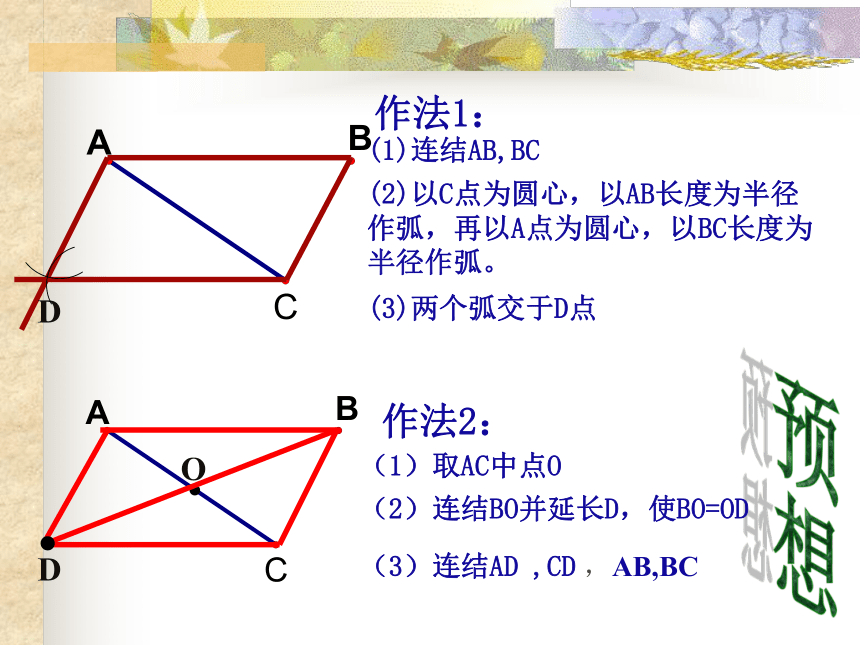
D预想作法1:(1)连结AB,BC (2)以C点为圆心,以AB长度为半径作弧,再以A点为圆心,以BC长度为半径作弧。
(3)两个弧交于D点 DO作法2:(1)取AC中点O(2)连结BO并延长D,使BO=OD (3)连结AD ,CD ,AB,BC已知:在四边形ABCD中,
AB=DC,AD=BC
求证:四边形ABCD是平行四边形 证明思路 :⊿ABC≌⊿CDA AB∥CD, AD∥BC ∴四边形ABCD是平行四边形 平行四边形的判定定理 1:两组对边分别相等的四边形是平行四边形 符号语言:
∵AB = CD,AD = BC(已知)
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形 )已知:在四边形ABCD中,
AO=OC, OB=OD
求证:四边形ABCD是平行四边形证明思路:
⊿AOB≌⊿COD(SAS) ⊿BOC≌⊿DOA (SAS)AB∥CD BC∥AD 四边形ABCD是平行四边形
平行四边形的判定定理2: 对角线互相平分的四边形是平行四边形 符号语言:
∵对角线AC,BD相交于O点
AO = CO ,BO = DO (已知)
∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形)
?
三、落实基础,巩固新知 ?练习1:
已知:在平行四边形ABCD中,BE=DF
求证:四边形AECF是平行四边形
练习2:
已知:在平行四边形ABCD中,对角线AC上取两点E,F.使
AE = CF.
求证:四边形DEBF是平行四边形。 O强调:
对角线是解决四边形问题中常用的辅助线。试一试:
已知:在平行四边形ABCD中,对角线AC与BD交于O点,
点E,G,F,H分别是AO,BO,CO,DO的中点,
?第1问:以图中标有字母的点为顶点,你能画出几个平行
四边形? 四、灵活应用新知 第2问:你能否验证图中所得到的新的四边形是平行四边形吗? 图(1)图(2)图(3)六、课后小结: 1、通过本节课的学习,同学们有了哪些收获?提示:在今后解决平行四边形问题时要尽可能地运用平行四边形的相应定理,不要总是依赖于全等三角形,否则不利于掌握新知识 本堂所讲的判定定理有:两组对边分别相等 对角线互相平分的四边形是平行四边形七、课后作业: 请你试着猜想一下,还会有哪些条件能够
判定平行四边形?请你验证自己的猜想。
谢谢各位老师!
并会运用判定定理解决相关问题。 教学目标:过程与方法: 1、经历对平行四边形判定方法的探究,使学生掌握并学会简单应用.
2、培养学生观察、分析、归纳的能力,养成勇于探索敢于创新的良好习惯,以及培养用数学方法分析、解决实际问题的能力,发展合情推理能力和说理能力。 教学目标:情感与态度: 学生通过观察、试验、类比、获得数学的猜想,体验数学活动充满着探索性和创造性,感受证明的必要性,证明过程的严谨性以及结论的准确性。发展学生克服困难的意志,通过一题多解激发学生的学习兴趣。 教学重点:掌握平行四边形的判定定理及其应用 教学难点:平行四边形判定定理的探究和归纳。 难点突破: 通过问题情境的设计,课堂实验研讨,引导学生发现、分析和解决问题。 教学方法: 合作探究式教学方法教学用具:多媒体辅助教学 教学过程:一、复习知识,导入新知 四边形ABCD具备怎样的条件就能判定它是平行四边形? ∵AB∥CD ,AD∥BC(已知)
∴四边形ABCD是平行四边形
(平行四边形定义) 具备“两组对边分别平行”的条件就可以判定四边形是平行四边形。 二、创设情景,探索新知 教学过程:探究活动:
已知一条线段AC,以线段AC为一条对角线,在线段AC的一侧有一点B,你能在线段AC的另一侧找到一点D,使得ABCD为平行四边形吗?
D预想作法1:(1)连结AB,BC (2)以C点为圆心,以AB长度为半径作弧,再以A点为圆心,以BC长度为半径作弧。
(3)两个弧交于D点 DO作法2:(1)取AC中点O(2)连结BO并延长D,使BO=OD (3)连结AD ,CD ,AB,BC已知:在四边形ABCD中,
AB=DC,AD=BC
求证:四边形ABCD是平行四边形 证明思路 :⊿ABC≌⊿CDA AB∥CD, AD∥BC ∴四边形ABCD是平行四边形 平行四边形的判定定理 1:两组对边分别相等的四边形是平行四边形 符号语言:
∵AB = CD,AD = BC(已知)
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形 )已知:在四边形ABCD中,
AO=OC, OB=OD
求证:四边形ABCD是平行四边形证明思路:
⊿AOB≌⊿COD(SAS) ⊿BOC≌⊿DOA (SAS)AB∥CD BC∥AD 四边形ABCD是平行四边形
平行四边形的判定定理2: 对角线互相平分的四边形是平行四边形 符号语言:
∵对角线AC,BD相交于O点
AO = CO ,BO = DO (已知)
∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形)
?
三、落实基础,巩固新知 ?练习1:
已知:在平行四边形ABCD中,BE=DF
求证:四边形AECF是平行四边形
练习2:
已知:在平行四边形ABCD中,对角线AC上取两点E,F.使
AE = CF.
求证:四边形DEBF是平行四边形。 O强调:
对角线是解决四边形问题中常用的辅助线。试一试:
已知:在平行四边形ABCD中,对角线AC与BD交于O点,
点E,G,F,H分别是AO,BO,CO,DO的中点,
?第1问:以图中标有字母的点为顶点,你能画出几个平行
四边形? 四、灵活应用新知 第2问:你能否验证图中所得到的新的四边形是平行四边形吗? 图(1)图(2)图(3)六、课后小结: 1、通过本节课的学习,同学们有了哪些收获?提示:在今后解决平行四边形问题时要尽可能地运用平行四边形的相应定理,不要总是依赖于全等三角形,否则不利于掌握新知识 本堂所讲的判定定理有:两组对边分别相等 对角线互相平分的四边形是平行四边形七、课后作业: 请你试着猜想一下,还会有哪些条件能够
判定平行四边形?请你验证自己的猜想。
谢谢各位老师!
同课章节目录
