16.1四边形课件(北京课改版八年级下)
文档属性
| 名称 | 16.1四边形课件(北京课改版八年级下) |
|
|
| 格式 | rar | ||
| 文件大小 | 229.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-21 00:00:00 | ||
图片预览


文档简介
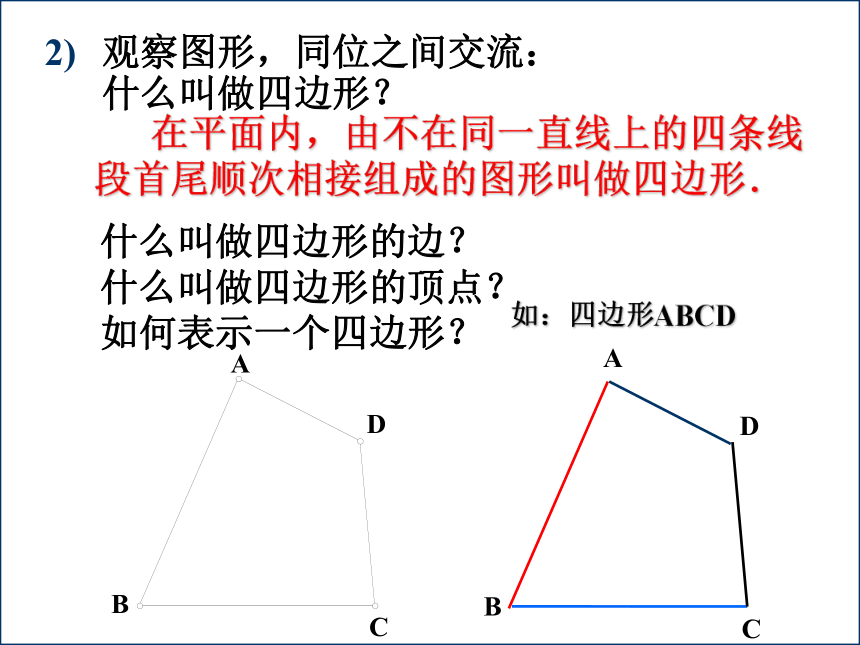
课件19张PPT。1.引入课题 四边形2. 四边形的有关概念请同学们回忆三角形的定义;三角形的边、顶点、角;三角形的表示方法;三角形中的重要线段. 由不在同一直线上的三条线段首尾顺次相接组成的图形叫做三角形.观察图形,同位之间交流:
什么叫做四边形?
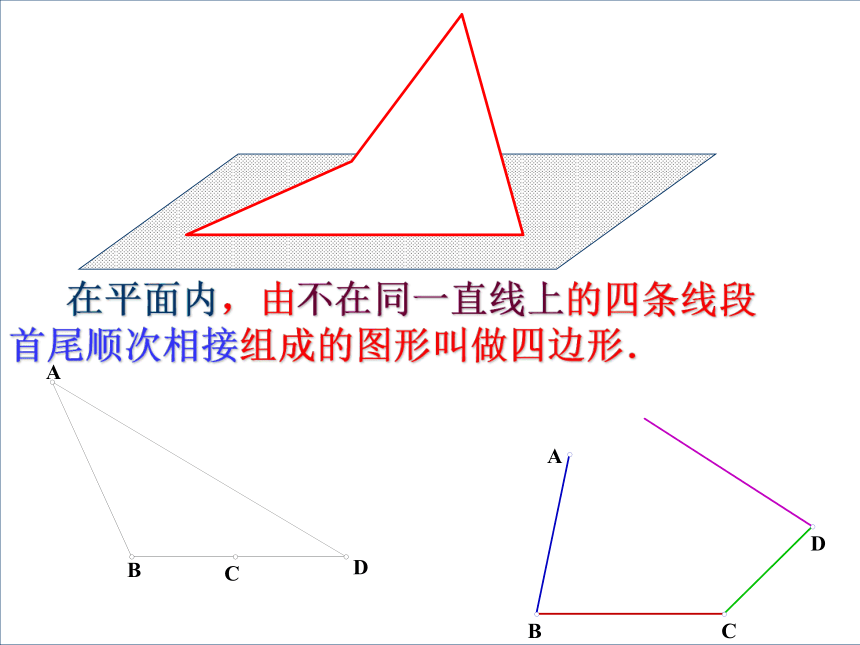
在平面内,由不在同一直线上的四条线段首尾顺次相接组成的图形叫做四边形.什么叫做四边形的边?
什么叫做四边形的顶点?
如何表示一个四边形?如:四边形ABCD 在平面内,由不在同一直线上的四条线段
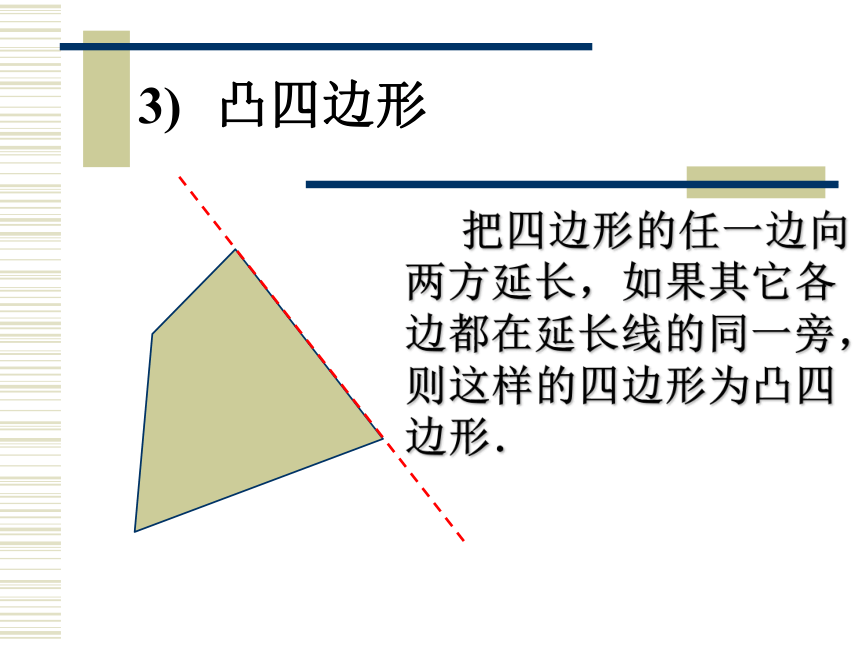
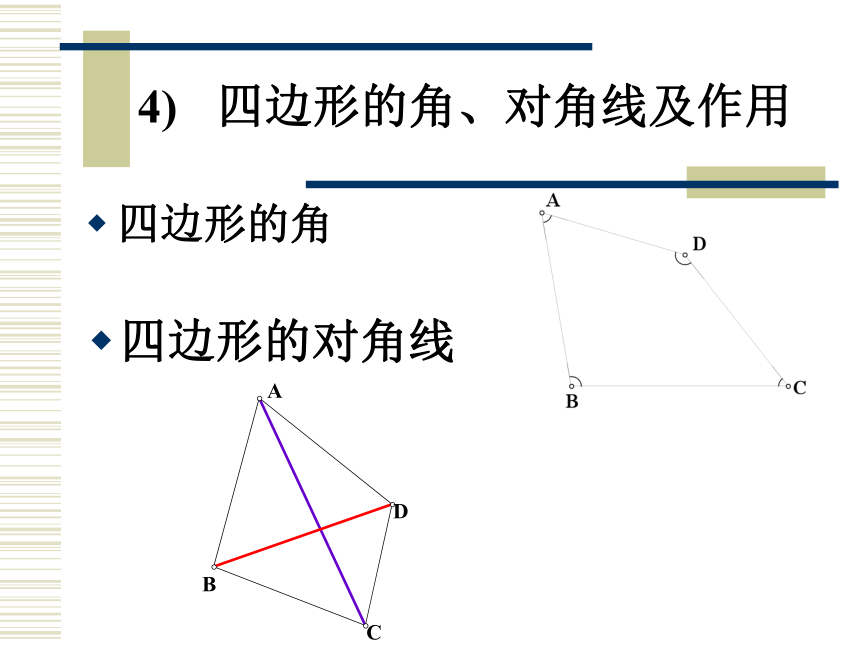
首尾顺次相接组成的图形叫做四边形.凸四边形 把四边形的任一边向两方延长,如果其它各边都在延长线的同一旁,则这样的四边形为凸四边形.下图是不是凸四边形? 把四边形的任一边向两方延长,如果其它各边不在延长线的同一旁,则这样的四边形为凹四边形.四边形的角、对角线及作用四边形的角四边形的对角线四边形的内角和等于多少度?问题: ∠ A+ ∠ B+ ∠C + ∠D=?四边形的内角和定理: 四边形的内角和等于360°. 关于四边形的内角和定理,
你能想出其它证明方案吗? 注意:
研究四边形时,常作它的对角线,把四边形问题转化为三角形问题.例题已知:如图,直线OB⊥AB,垂足为B,直线OC⊥AC,垂足为C. 求证:(1)∠1+ ∠ A=180°; (2) ∠ A= ∠2.已知:如图,直线OB⊥AB,垂足为B,直线OC⊥AC,垂足为C. 求证:(1)∠1+ ∠ A=180°; (2) ∠ A= ∠2.证明: (1)∵ ∠ A+ ∠ACO + ∠1 + ∠ABO=360°,
∴ ∠1+ ∠ A=360°-90°-90°=180°(四边形的内角和等于360°)(2) ∵ ∠1+ ∠ A=180°,
∠1+ ∠ 2=180°,∴ ∠ A= ∠2.
∵ OB⊥AB OC⊥AC
∴ ∠ACO= ∠ABO =90°,练习已知:如图,在四边形ABCD中,∠A= ∠C=90°,BE平分∠B,DF平分∠D.问BE与DF是否平行?为什么?练习(1)四边形的四个内角可以都是锐角吗?可以都是钝角吗?可以都是直角吗?为什么? (2)一个四边形中,最多可以有几个锐角?几个钝角?练习能否用相同形状的任意四边形地砖铺地?请说明理由? 能否用相同形状的任意四边形地砖铺地?请说明理由?答:根据任意四边形的内角和为360度,可如下图一样拼图。小结什么叫四边形?
四边形的内角和定理. 在研究四边形时,常通过作它的对角线,把关于四边形的问题转化为关于三角形的问题来解决.思考题如果一个四边形四个内角之比是2∶2∶3∶5,那么这个四边形的四个内角中 (A)只有一个直角 (B)只有一个锐角 (C)有两个直角 (D)有两个钝角
若一个角的两边与令一个角的两边互相垂直,且中两个角的差为46°,那么这两个角的度数分别为_________.?
首尾顺次相接组成的图形叫做四边形.凸四边形 把四边形的任一边向两方延长,如果其它各边都在延长线的同一旁,则这样的四边形为凸四边形.下图是不是凸四边形? 把四边形的任一边向两方延长,如果其它各边不在延长线的同一旁,则这样的四边形为凹四边形.四边形的角、对角线及作用四边形的角四边形的对角线四边形的内角和等于多少度?问题: ∠ A+ ∠ B+ ∠C + ∠D=?四边形的内角和定理: 四边形的内角和等于360°. 关于四边形的内角和定理,
你能想出其它证明方案吗? 注意:
研究四边形时,常作它的对角线,把四边形问题转化为三角形问题.例题已知:如图,直线OB⊥AB,垂足为B,直线OC⊥AC,垂足为C. 求证:(1)∠1+ ∠ A=180°; (2) ∠ A= ∠2.已知:如图,直线OB⊥AB,垂足为B,直线OC⊥AC,垂足为C. 求证:(1)∠1+ ∠ A=180°; (2) ∠ A= ∠2.证明: (1)∵ ∠ A+ ∠ACO + ∠1 + ∠ABO=360°,
∴ ∠1+ ∠ A=360°-90°-90°=180°(四边形的内角和等于360°)(2) ∵ ∠1+ ∠ A=180°,
∠1+ ∠ 2=180°,∴ ∠ A= ∠2.
∵ OB⊥AB OC⊥AC
∴ ∠ACO= ∠ABO =90°,练习已知:如图,在四边形ABCD中,∠A= ∠C=90°,BE平分∠B,DF平分∠D.问BE与DF是否平行?为什么?练习(1)四边形的四个内角可以都是锐角吗?可以都是钝角吗?可以都是直角吗?为什么? (2)一个四边形中,最多可以有几个锐角?几个钝角?练习能否用相同形状的任意四边形地砖铺地?请说明理由? 能否用相同形状的任意四边形地砖铺地?请说明理由?答:根据任意四边形的内角和为360度,可如下图一样拼图。小结什么叫四边形?
四边形的内角和定理. 在研究四边形时,常通过作它的对角线,把关于四边形的问题转化为关于三角形的问题来解决.思考题如果一个四边形四个内角之比是2∶2∶3∶5,那么这个四边形的四个内角中 (A)只有一个直角 (B)只有一个锐角 (C)有两个直角 (D)有两个钝角
若一个角的两边与令一个角的两边互相垂直,且中两个角的差为46°,那么这两个角的度数分别为_________.?
同课章节目录
