【沪科版八上同步练习】13.1 三角形中的边角关系(含答案)
文档属性
| 名称 | 【沪科版八上同步练习】13.1 三角形中的边角关系(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 7.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-19 07:24:48 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【沪科版八上同步练习】
13.1三角形中的边角关系
一、单选题
1.在中,若,,则是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
2.若一个三角形的两边长分别是5和8,则其第三条边长可能是( )
A.15 B.10 C.3 D.1
3.若一个三角形的两边长分别为4和9,则第三边长可能是( )
A.3 B.4 C.5 D.11
4.如图,已知AD∥CD,∠1=109°,∠2=120°,则∠α的度数是( )
A.38° B.48° C.49° D.60°
5.△ABC中,∠A=∠B>∠C,则△ABC是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.都有可能
二、填空题
6. 如图,是的一条中线,若,则 .
7.在中,,则最大的内角为 度.
8.如图,AB∥CD,CB平分∠ACD,若∠BCD=35°,则∠A的度数为 .
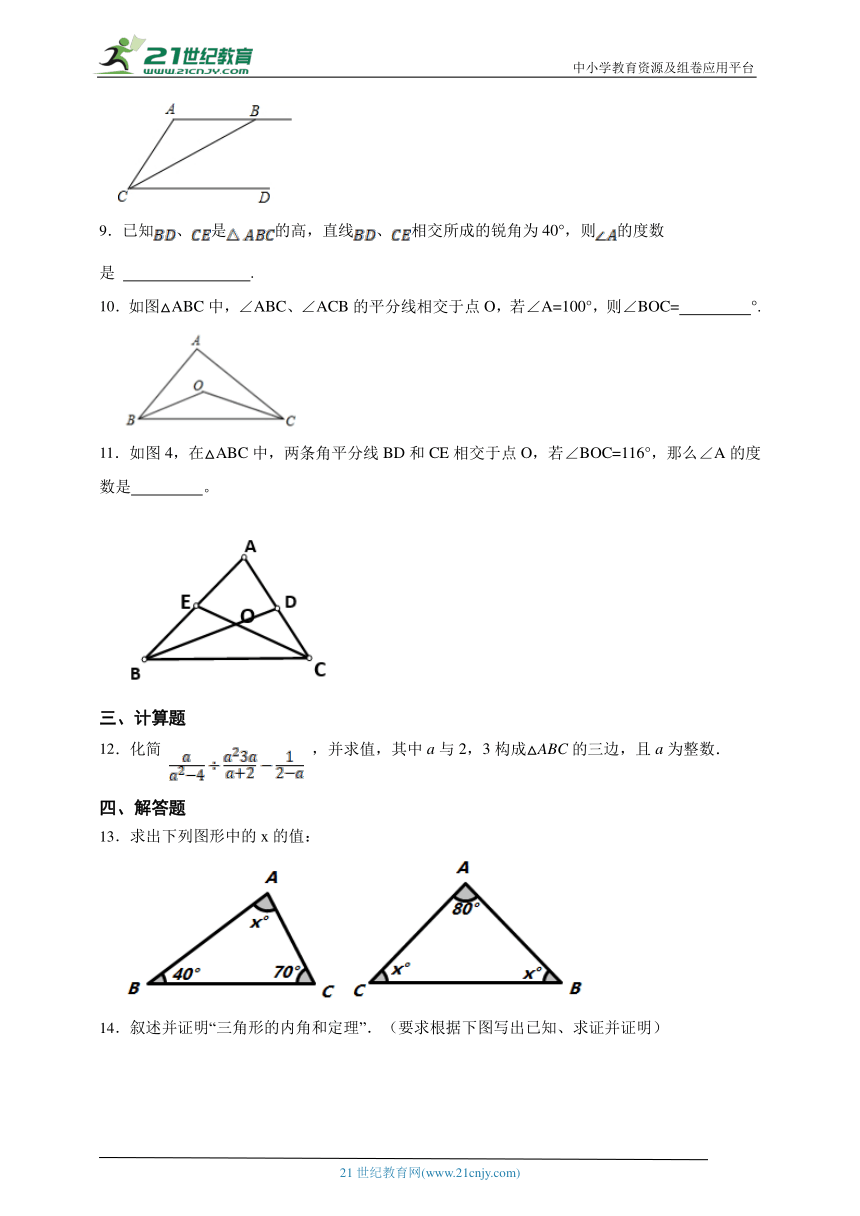
9.已知、是的高,直线、相交所成的锐角为40°,则的度数是 .
10.如图△ABC中,∠ABC、∠ACB的平分线相交于点O,若∠A=100°,则∠BOC= °.
11.如图4,在△ABC中,两条角平分线BD和CE相交于点O,若∠BOC=116°,那么∠A的度数是 。
三、计算题
12.化简 ,并求值,其中a与2,3构成△ABC的三边,且a为整数.
四、解答题
13.求出下列图形中的x的值:
14.叙述并证明“三角形的内角和定理”.(要求根据下图写出已知、求证并证明)
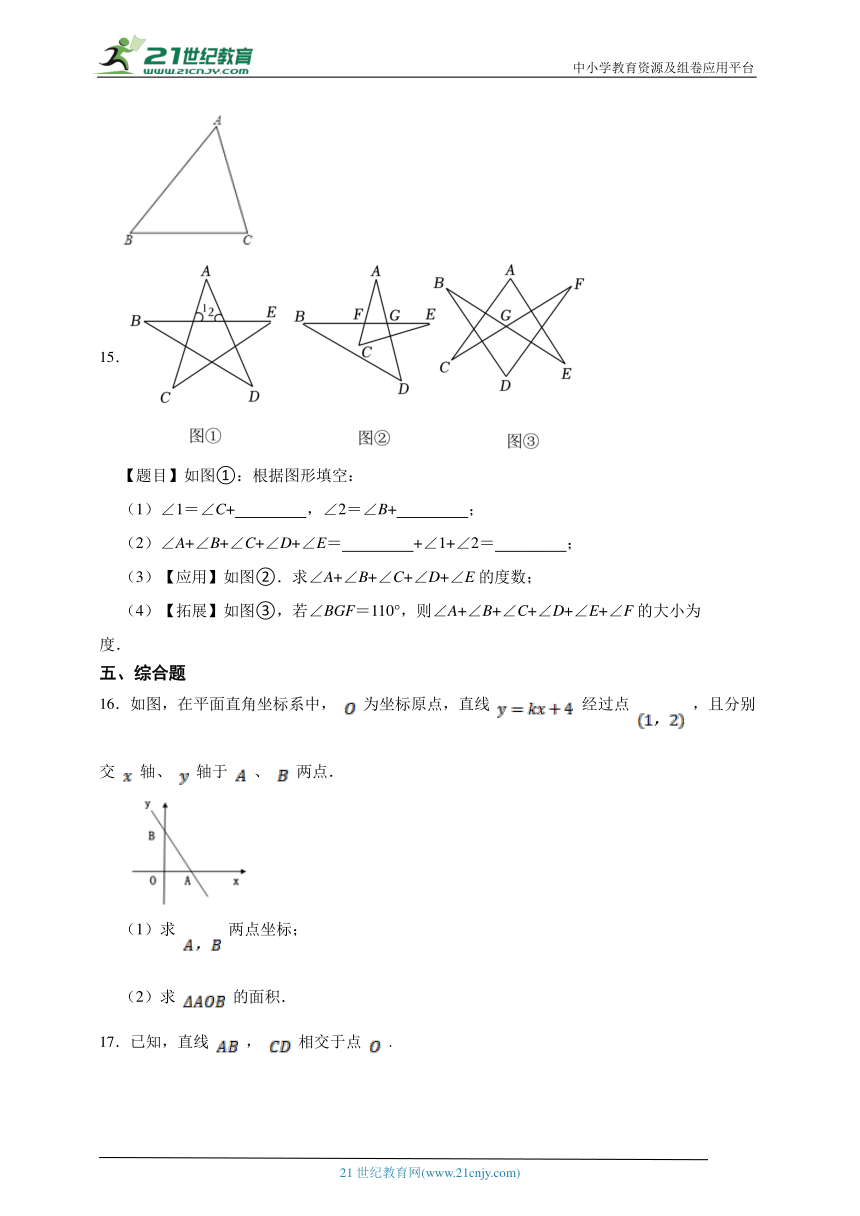
15.
【题目】如图①:根据图形填空:
(1)∠1=∠C+ ,∠2=∠B+ ;
(2)∠A+∠B+∠C+∠D+∠E= +∠1+∠2= ;
(3)【应用】如图②.求∠A+∠B+∠C+∠D+∠E的度数;
(4)【拓展】如图③,若∠BGF=110°,则∠A+∠B+∠C+∠D+∠E+∠F的大小为 度.
五、综合题
16.如图,在平面直角坐标系中, 为坐标原点,直线 经过点 ,且分别交 轴、 轴于 、 两点.
(1)求 两点坐标;
(2)求 的面积.
17.已知,直线 , 相交于点 .
(1)如图1,若 平分 , ,求 的度数;
(2)如图2, 交 于点 ,交 于点 ,且 , ,求 的度数.
18.综合与探究
如图,在平面直角坐标系中,直线 与x轴、y轴分别交于点 、点 ,以线段 为直角边在第一象限内作等腰直角三角形 , .
(1)求直线 的解析式;
(2)求出 的面积;
(3)若 为坐标系中第一象限的一个动点,连结 、 .当 与 面积相等时,求m的值.
六、实践探究题
19.如图1,自行车尾灯是由塑料罩片包裹的若干个小平面镜组成,利用平面镜反射光线,以提醒后方车辆注意.小亮所在学习小组对其工作原理进行探究,发现以下规律:如图2,为平面镜,分别为入射光线和反射光线,则.请继续以下探究:
(1)探究反射规律
①如图3,,则 ▲ (用含的代数式表示).
②若光线,判断与的位置关系,并说明理由.
(2)模拟应用研究
在行驶过程中,后车驾驶员平视前方,且视点会高于反射点(如图4),因此小亮认为反射光线应与水平视线成一定角度.学习小组设计了如图5所示的模拟实验装置,使入射光线,当与所成夹角为时,求的度数.
答案解析部分
1.【答案】B
【知识点】三角形内角和定理
2.【答案】B
【知识点】三角形三边关系
3.【答案】D
【知识点】三角形三边关系
4.【答案】C
【知识点】平行线的性质;三角形的外角性质
5.【答案】A
【知识点】三角形内角和定理
6.【答案】10
【知识点】三角形的角平分线、中线和高
7.【答案】90
【知识点】三角形内角和定理
8.【答案】110°
【知识点】平行线的性质;三角形内角和定理
9.【答案】140°或40°
【知识点】三角形的角平分线、中线和高
10.【答案】140
【知识点】三角形的角平分线、中线和高;三角形内角和定理
11.【答案】52°
【知识点】三角形内角和定理;角平分线的概念
12.【答案】解:原式= , ∵a与2,3构成△ABC的三边, ∴1<a<5,且a为整数,∴a=2,3,4, 又∵a≠2且a≠3,∴a=4, 当a=4时,原式=1
【知识点】分式的化简求值;三角形三边关系
13.【答案】解:在△ABC中,∠A+∠B+∠C=180°,
∵∠B=40°, ∠C=70°,
∴∠A=180°-∠B-∠C=180°-40°-70°=70°,
∴x=40;
在△ABC中,∠A+∠B+∠C=180°,
∵∠A=80°,
∴80°+x°+x° =180°,
∴x=50.
【知识点】三角形内角和定理
14.【答案】证明:过点A作直线MN,使MN∥BC.
∵MN∥BC,
∴∠B=∠MAB,∠C=∠NAC(两直线平行,内错角相等)
∵∠MAB+∠NAC+∠BAC=180°(平角定义)
∴∠B+∠C+∠BAC=180°(等量代换)
即∠A+∠B+∠C=180°.
【知识点】三角形内角和定理
15.【答案】(1)∠E;∠D
(2)∠A;180°
(3)解:∵∠AFG=∠C+∠E,∠AGF=∠B+∠D,
∴∠A+∠B+∠C+∠D+∠E=∠A+∠AFG+∠AGF=180°;
(4)220
【知识点】角的运算;三角形的外角性质
16.【答案】(1)解:把(1,2)代入 得,
,
解得 ,
∴一次函数的解析式为y= 2x+4;
当x=0时,y=4,
∴点B的坐标为(0,4),
当y=0时,x=2,
∴点A的坐标为(2,0).
答:A(2,0),B(0,4);
(2)解:∵点A、B的坐标分别为(2,0)、(0,4),
∴OA=2,OB=4,
∴ ,
答:△AOB的面积为4;
【知识点】待定系数法求一次函数解析式;三角形的面积
17.【答案】(1)解:设∠EOC= ,∠EOD= ,
根据题意得 ,
解得: ,
∴ ,
∵OA平分∠EOC,
∴ ,
∴ .
(2)解:∵ , ,
∴①,
∵②,
联立①②解得: ,
∴③,
又∵④,
联立③④解得: , ,
∵MN∥CD
∴ .
【知识点】余角、补角及其性质;角的大小比较;平行线的性质;三角形内角和定理;角平分线的概念
18.【答案】(1)解:设直线 的表达式为:
则 ,解得
故直线l的表达式应为
(2)解:在 中,
由勾股定理得:
∵ 为等腰直角三角形,
∴
(3)解:连接 、 、 ,如图:
∵
∴
即 ,解得
故当 与 面积相等时,m的值为 .
【知识点】待定系数法求一次函数解析式;三角形的面积;一次函数中的动态几何问题
19.【答案】(1)解:①75°-α
②EF⊥FG,理由如下:
∵∠ABE+∠ABC+∠CBF=180°,∠ABE=∠CBF,
∴∠ABC=180°-2∠CBF,
同理,∠DCB=180°-2∠BCF,
∵AB∥CD,
∴∠ABC+∠DCB=180°,
即180°-2∠CBF+180°-2∠BCF=180°,
∴∠CBF+∠BCF=90°,
∴∠BFC=180°-90°=90°,
∴EF⊥FG.
(2)解: 延长BC交DH于点M,如图:
∵∠MDC+∠M+∠MCD=180°,
∴∠M+∠MCD=180°-∠MDC=165°,
∵MD∥AB,
∴∠M+∠MBA=180°,
∵∠MCD+∠DCB=180°,
∴∠DCB+∠CBA=180°-∠MCD+180°-∠M=360°-165°=195°,
∴,
∴∠BFC=180°-∠FCB-∠CBF=97.5°.
【知识点】平行线的性质;三角形内角和定理
v
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【沪科版八上同步练习】
13.1三角形中的边角关系
一、单选题
1.在中,若,,则是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
2.若一个三角形的两边长分别是5和8,则其第三条边长可能是( )
A.15 B.10 C.3 D.1
3.若一个三角形的两边长分别为4和9,则第三边长可能是( )
A.3 B.4 C.5 D.11
4.如图,已知AD∥CD,∠1=109°,∠2=120°,则∠α的度数是( )
A.38° B.48° C.49° D.60°
5.△ABC中,∠A=∠B>∠C,则△ABC是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.都有可能
二、填空题
6. 如图,是的一条中线,若,则 .
7.在中,,则最大的内角为 度.
8.如图,AB∥CD,CB平分∠ACD,若∠BCD=35°,则∠A的度数为 .
9.已知、是的高,直线、相交所成的锐角为40°,则的度数是 .
10.如图△ABC中,∠ABC、∠ACB的平分线相交于点O,若∠A=100°,则∠BOC= °.
11.如图4,在△ABC中,两条角平分线BD和CE相交于点O,若∠BOC=116°,那么∠A的度数是 。
三、计算题
12.化简 ,并求值,其中a与2,3构成△ABC的三边,且a为整数.
四、解答题
13.求出下列图形中的x的值:
14.叙述并证明“三角形的内角和定理”.(要求根据下图写出已知、求证并证明)
15.
【题目】如图①:根据图形填空:
(1)∠1=∠C+ ,∠2=∠B+ ;
(2)∠A+∠B+∠C+∠D+∠E= +∠1+∠2= ;
(3)【应用】如图②.求∠A+∠B+∠C+∠D+∠E的度数;
(4)【拓展】如图③,若∠BGF=110°,则∠A+∠B+∠C+∠D+∠E+∠F的大小为 度.
五、综合题
16.如图,在平面直角坐标系中, 为坐标原点,直线 经过点 ,且分别交 轴、 轴于 、 两点.
(1)求 两点坐标;
(2)求 的面积.
17.已知,直线 , 相交于点 .
(1)如图1,若 平分 , ,求 的度数;
(2)如图2, 交 于点 ,交 于点 ,且 , ,求 的度数.
18.综合与探究
如图,在平面直角坐标系中,直线 与x轴、y轴分别交于点 、点 ,以线段 为直角边在第一象限内作等腰直角三角形 , .
(1)求直线 的解析式;
(2)求出 的面积;
(3)若 为坐标系中第一象限的一个动点,连结 、 .当 与 面积相等时,求m的值.
六、实践探究题
19.如图1,自行车尾灯是由塑料罩片包裹的若干个小平面镜组成,利用平面镜反射光线,以提醒后方车辆注意.小亮所在学习小组对其工作原理进行探究,发现以下规律:如图2,为平面镜,分别为入射光线和反射光线,则.请继续以下探究:
(1)探究反射规律
①如图3,,则 ▲ (用含的代数式表示).
②若光线,判断与的位置关系,并说明理由.
(2)模拟应用研究
在行驶过程中,后车驾驶员平视前方,且视点会高于反射点(如图4),因此小亮认为反射光线应与水平视线成一定角度.学习小组设计了如图5所示的模拟实验装置,使入射光线,当与所成夹角为时,求的度数.
答案解析部分
1.【答案】B
【知识点】三角形内角和定理
2.【答案】B
【知识点】三角形三边关系
3.【答案】D
【知识点】三角形三边关系
4.【答案】C
【知识点】平行线的性质;三角形的外角性质
5.【答案】A
【知识点】三角形内角和定理
6.【答案】10
【知识点】三角形的角平分线、中线和高
7.【答案】90
【知识点】三角形内角和定理
8.【答案】110°
【知识点】平行线的性质;三角形内角和定理
9.【答案】140°或40°
【知识点】三角形的角平分线、中线和高
10.【答案】140
【知识点】三角形的角平分线、中线和高;三角形内角和定理
11.【答案】52°
【知识点】三角形内角和定理;角平分线的概念
12.【答案】解:原式= , ∵a与2,3构成△ABC的三边, ∴1<a<5,且a为整数,∴a=2,3,4, 又∵a≠2且a≠3,∴a=4, 当a=4时,原式=1
【知识点】分式的化简求值;三角形三边关系
13.【答案】解:在△ABC中,∠A+∠B+∠C=180°,
∵∠B=40°, ∠C=70°,
∴∠A=180°-∠B-∠C=180°-40°-70°=70°,
∴x=40;
在△ABC中,∠A+∠B+∠C=180°,
∵∠A=80°,
∴80°+x°+x° =180°,
∴x=50.
【知识点】三角形内角和定理
14.【答案】证明:过点A作直线MN,使MN∥BC.
∵MN∥BC,
∴∠B=∠MAB,∠C=∠NAC(两直线平行,内错角相等)
∵∠MAB+∠NAC+∠BAC=180°(平角定义)
∴∠B+∠C+∠BAC=180°(等量代换)
即∠A+∠B+∠C=180°.
【知识点】三角形内角和定理
15.【答案】(1)∠E;∠D
(2)∠A;180°
(3)解:∵∠AFG=∠C+∠E,∠AGF=∠B+∠D,
∴∠A+∠B+∠C+∠D+∠E=∠A+∠AFG+∠AGF=180°;
(4)220
【知识点】角的运算;三角形的外角性质
16.【答案】(1)解:把(1,2)代入 得,
,
解得 ,
∴一次函数的解析式为y= 2x+4;
当x=0时,y=4,
∴点B的坐标为(0,4),
当y=0时,x=2,
∴点A的坐标为(2,0).
答:A(2,0),B(0,4);
(2)解:∵点A、B的坐标分别为(2,0)、(0,4),
∴OA=2,OB=4,
∴ ,
答:△AOB的面积为4;
【知识点】待定系数法求一次函数解析式;三角形的面积
17.【答案】(1)解:设∠EOC= ,∠EOD= ,
根据题意得 ,
解得: ,
∴ ,
∵OA平分∠EOC,
∴ ,
∴ .
(2)解:∵ , ,
∴①,
∵②,
联立①②解得: ,
∴③,
又∵④,
联立③④解得: , ,
∵MN∥CD
∴ .
【知识点】余角、补角及其性质;角的大小比较;平行线的性质;三角形内角和定理;角平分线的概念
18.【答案】(1)解:设直线 的表达式为:
则 ,解得
故直线l的表达式应为
(2)解:在 中,
由勾股定理得:
∵ 为等腰直角三角形,
∴
(3)解:连接 、 、 ,如图:
∵
∴
即 ,解得
故当 与 面积相等时,m的值为 .
【知识点】待定系数法求一次函数解析式;三角形的面积;一次函数中的动态几何问题
19.【答案】(1)解:①75°-α
②EF⊥FG,理由如下:
∵∠ABE+∠ABC+∠CBF=180°,∠ABE=∠CBF,
∴∠ABC=180°-2∠CBF,
同理,∠DCB=180°-2∠BCF,
∵AB∥CD,
∴∠ABC+∠DCB=180°,
即180°-2∠CBF+180°-2∠BCF=180°,
∴∠CBF+∠BCF=90°,
∴∠BFC=180°-90°=90°,
∴EF⊥FG.
(2)解: 延长BC交DH于点M,如图:
∵∠MDC+∠M+∠MCD=180°,
∴∠M+∠MCD=180°-∠MDC=165°,
∵MD∥AB,
∴∠M+∠MBA=180°,
∵∠MCD+∠DCB=180°,
∴∠DCB+∠CBA=180°-∠MCD+180°-∠M=360°-165°=195°,
∴,
∴∠BFC=180°-∠FCB-∠CBF=97.5°.
【知识点】平行线的性质;三角形内角和定理
v
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
