1.1.1分子动理论的基本内容(一) 课件(共35张PPT)
文档属性
| 名称 | 1.1.1分子动理论的基本内容(一) 课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 230.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-06-18 00:00:00 | ||
图片预览











文档简介
分子动理论的基本观点(一)
第一章 分子动理论与气体实验定律
置身花海,你有没有想过,为什么能够闻到这沁人心脾的香味呢?
古希腊学者德谟克利特作出了解释:“花的原子”飘到了人们鼻子里。
热学就是研究物质热运动规律及其应用的一门学科,是物理学的一个重要组成部分。
“花的原子”究竟是怎么运动的?
热运动
2
知道两种分子模型,体会建立物理模型在研究物理问题中的作用
1
认识物体是由大量分子组成的
重点
重难点
3
知道阿伏伽德罗常数及其意义,会用阿伏伽德罗常数进行计算或估算
重点
物体由大量分子组成
如图,如果我们把地球的大小与一个苹果的大小相比,那就相当于将直径为1cm 的球与分子相比。可见,分子是极其微小的。那么,构成物体的微小分子到底小到什么程度?我们该如何观察与计量呢?
两千多年前,古希腊的著名思想家德谟克利特说:万物都是由极小的微粒组成的。科学技术发展到现在,这种猜想已被证实。
1.分子的大小
(1)热学中的分子:当探讨 、 或 等微观粒子的热运动时,通常将它们统称为分子。
分子
原子
离子
电子扫描隧道显微镜
(放大几亿倍)
怎样才能看到分子?
观察方法:用肉眼和高倍的光学显微镜都无法看到,只有用扫描隧道显微镜才能观察到物质表面原子的排列。
我国科学家用扫描隧道显微镜拍摄的石墨表面原子的排布图,图中的每个亮斑都是一个碳原子。
我国科学家在1993年首次利用超真空扫描隧道显微镜技术,在一块晶体硅的表面直接移动硅原子写下了”中国“ 两字。
扫描隧道显微镜的针尖在铜表面上操纵48个原子使它们排成圆形
(2)一般分子直径的数量级为 m。
除一些有机物质的大分子外
10-10
2.阿伏伽德罗常数
(1)定义:1 mol任何物质都含有 的粒子数,这个数量称为阿伏伽德罗常数。
(2)数值:NA= 。
相同
6.02×1023 mol-1
宏观量
微观量
宏观量
微观量
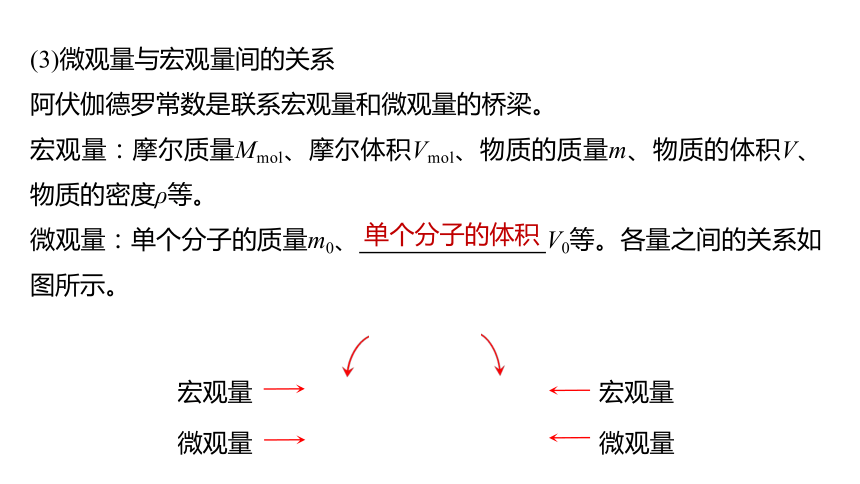
(3)微观量与宏观量间的关系
阿伏伽德罗常数是联系宏观量和微观量的桥梁。
宏观量:摩尔质量Mmol、摩尔体积Vmol、物质的质量m、物质的体积V、物质的密度ρ等。
微观量:单个分子的质量m0、 V0等。各量之间的关系如图所示。
单个分子的体积
若某种物质的摩尔质量为M,质量为m,摩尔体积为Vmol,体积为V,密度为ρ,假设分子紧密排列,请总结微观量与宏观量的关系(已知阿伏伽德罗常数为NA)。
(1)分子质量:m0= = 。
(2)分子体积:V0= = 。
(3)物质所含的分子数:N= = = 。
nNA
(4)ρ= = 。
(1)物体是由大量分子组成的,分子是不可再分的最小单元。( )
(2)本节所说的“分子”,既包含化学中的分子,也包含原子和离子。
( )
×
√
1.(多选)用M表示液体或固体的摩尔质量,m表示分子质量,ρ表示物质密度,Vmol表示摩尔体积,V0表示分子体积。NA表示阿伏伽德罗常数,下列关系式正确的是
√
√
√
2.(2023·苏州市高二月考)阿伏伽德罗常数是NA(mol-1),铜的摩尔质量是μ(kg/mol),铜的密度是ρ(kg/m3),则下列说法不正确的是
√
两种分子模型
简化
球体模型
立方体模型
蛋白质分子结构模型
C60分子
?
双螺旋结构的DNA分子模型
1.球体模型:固体和液体可看作一个一个 球形分子排列而成,忽略 ,如图所示。
两种分子模型
紧挨着的
分子间空隙
d
d
d
d
一个分子的直径
d
2.立方体模型:气体分子间的空隙很大,把气体分成若干个小立方体,气体分子位于每个小立方体的中心,每个小立方体是每个气体分子平均占有的 ,如图所示。
d
d
d
气体分子间的平均距离
活动空间
关系式Vmol=NAV0(V0为一个分子的体积,Vmol为摩尔体积),对于任何物质都成立吗?
答案 关系式Vmol=NAV0仅适用于固体和液体,不适用于气体。对于固体和液体,可认为分子紧密排列,分子间没有空隙,如图甲,则Vmol=NAV0。对于气体来说,分子间的距离远大于分子的直径。V0应为每个气体分子平均占有的空间体积,而不是每个气体分子的实际体积,如图乙。
3.(2023·邢台市高二期中)某一体积为V的密封容器,充入密度为ρ、摩尔质量为M的气体,阿伏伽德罗常数为NA。求:
(1)该容器中气体分子的总个数;
(2)气体分子中心间的平均距离;
(3)现将这部分气体压缩成液体,体积变为V0,分子直径大小(将液体分子视为球体模型)。
设气体分子中心间的平均距离为a,则有V1=a3
(3)该部分气体压缩成液体,分子个数不变,设每个液体分子的体积为V2,
4.已知氧气分子的质量m0=5.3×10-26 kg,标准状况下氧气的密度ρ=1.43 kg/m3,阿伏伽德罗常数NA=6.02×1023 mol-1,求:(计算结果均保留两位有效数字)
(1)氧气的摩尔质量;
(2)标准状况下氧气分子间的平均距离;
(3)标准状况下1 cm3的氧气中含有的氧气分子数。
答案 (1)3.2×10-2 kg/mol (2)3.3×10-9 m (3)2.7×1019个
(1)氧气的摩尔质量为
M=NAm0=6.02×1023×5.3×10-26 kg/mol≈3.2×10-2 kg/mol;
而每个氧气分子占有的体积可以看成是棱长为a的立方体,
(3) 1 cm3氧气的质量为
m=ρV=1.43×1×10-6 kg=1.43×10-6 kg
则1 cm3氧气中含有的氧气分子数
5.地球到月球的平均距离为3.8×105 km。已知铁的摩尔质量为5.6×10-2 kg/
mol,密度为7.9×103 kg/m3,阿伏伽德罗常数NA=6.02×1023 mol-1。若把铁原子一个紧挨一个地单列排起来,筑成从地球通往月球的“原子大道”。求:(π=3.14,计算结果保留三位有效数字)
(1)这条“原子大道”共需多少个铁原子?
(2)这条“原子大道”的质量为多少?
答案 (1)1.35×1018个 (2)1.26×10-7 kg
(1)铁原子为球形,设直径为d,
“原子大道”的铁原子数
(2)“原子大道”的质量
分子动理论的基本内容(一)
目标一
阿伏加德罗常数
1. 阿伏加德罗常数NA=6.02×1023 mol-1
2.微观量与宏观量的桥梁
1.球体模型(固体、液体)
2.立方体模型(气体)
目标二
两种分子模型
幽默一笑
闻到屎味,就意味着吸入屎分子嘛???
最精密的机器-光刻机
第一章 分子动理论与气体实验定律
置身花海,你有没有想过,为什么能够闻到这沁人心脾的香味呢?
古希腊学者德谟克利特作出了解释:“花的原子”飘到了人们鼻子里。
热学就是研究物质热运动规律及其应用的一门学科,是物理学的一个重要组成部分。
“花的原子”究竟是怎么运动的?
热运动
2
知道两种分子模型,体会建立物理模型在研究物理问题中的作用
1
认识物体是由大量分子组成的
重点
重难点
3
知道阿伏伽德罗常数及其意义,会用阿伏伽德罗常数进行计算或估算
重点
物体由大量分子组成
如图,如果我们把地球的大小与一个苹果的大小相比,那就相当于将直径为1cm 的球与分子相比。可见,分子是极其微小的。那么,构成物体的微小分子到底小到什么程度?我们该如何观察与计量呢?
两千多年前,古希腊的著名思想家德谟克利特说:万物都是由极小的微粒组成的。科学技术发展到现在,这种猜想已被证实。
1.分子的大小
(1)热学中的分子:当探讨 、 或 等微观粒子的热运动时,通常将它们统称为分子。
分子
原子
离子
电子扫描隧道显微镜
(放大几亿倍)
怎样才能看到分子?
观察方法:用肉眼和高倍的光学显微镜都无法看到,只有用扫描隧道显微镜才能观察到物质表面原子的排列。
我国科学家用扫描隧道显微镜拍摄的石墨表面原子的排布图,图中的每个亮斑都是一个碳原子。
我国科学家在1993年首次利用超真空扫描隧道显微镜技术,在一块晶体硅的表面直接移动硅原子写下了”中国“ 两字。
扫描隧道显微镜的针尖在铜表面上操纵48个原子使它们排成圆形
(2)一般分子直径的数量级为 m。
除一些有机物质的大分子外
10-10
2.阿伏伽德罗常数
(1)定义:1 mol任何物质都含有 的粒子数,这个数量称为阿伏伽德罗常数。
(2)数值:NA= 。
相同
6.02×1023 mol-1
宏观量
微观量
宏观量
微观量
(3)微观量与宏观量间的关系
阿伏伽德罗常数是联系宏观量和微观量的桥梁。
宏观量:摩尔质量Mmol、摩尔体积Vmol、物质的质量m、物质的体积V、物质的密度ρ等。
微观量:单个分子的质量m0、 V0等。各量之间的关系如图所示。
单个分子的体积
若某种物质的摩尔质量为M,质量为m,摩尔体积为Vmol,体积为V,密度为ρ,假设分子紧密排列,请总结微观量与宏观量的关系(已知阿伏伽德罗常数为NA)。
(1)分子质量:m0= = 。
(2)分子体积:V0= = 。
(3)物质所含的分子数:N= = = 。
nNA
(4)ρ= = 。
(1)物体是由大量分子组成的,分子是不可再分的最小单元。( )
(2)本节所说的“分子”,既包含化学中的分子,也包含原子和离子。
( )
×
√
1.(多选)用M表示液体或固体的摩尔质量,m表示分子质量,ρ表示物质密度,Vmol表示摩尔体积,V0表示分子体积。NA表示阿伏伽德罗常数,下列关系式正确的是
√
√
√
2.(2023·苏州市高二月考)阿伏伽德罗常数是NA(mol-1),铜的摩尔质量是μ(kg/mol),铜的密度是ρ(kg/m3),则下列说法不正确的是
√
两种分子模型
简化
球体模型
立方体模型
蛋白质分子结构模型
C60分子
?
双螺旋结构的DNA分子模型
1.球体模型:固体和液体可看作一个一个 球形分子排列而成,忽略 ,如图所示。
两种分子模型
紧挨着的
分子间空隙
d
d
d
d
一个分子的直径
d
2.立方体模型:气体分子间的空隙很大,把气体分成若干个小立方体,气体分子位于每个小立方体的中心,每个小立方体是每个气体分子平均占有的 ,如图所示。
d
d
d
气体分子间的平均距离
活动空间
关系式Vmol=NAV0(V0为一个分子的体积,Vmol为摩尔体积),对于任何物质都成立吗?
答案 关系式Vmol=NAV0仅适用于固体和液体,不适用于气体。对于固体和液体,可认为分子紧密排列,分子间没有空隙,如图甲,则Vmol=NAV0。对于气体来说,分子间的距离远大于分子的直径。V0应为每个气体分子平均占有的空间体积,而不是每个气体分子的实际体积,如图乙。
3.(2023·邢台市高二期中)某一体积为V的密封容器,充入密度为ρ、摩尔质量为M的气体,阿伏伽德罗常数为NA。求:
(1)该容器中气体分子的总个数;
(2)气体分子中心间的平均距离;
(3)现将这部分气体压缩成液体,体积变为V0,分子直径大小(将液体分子视为球体模型)。
设气体分子中心间的平均距离为a,则有V1=a3
(3)该部分气体压缩成液体,分子个数不变,设每个液体分子的体积为V2,
4.已知氧气分子的质量m0=5.3×10-26 kg,标准状况下氧气的密度ρ=1.43 kg/m3,阿伏伽德罗常数NA=6.02×1023 mol-1,求:(计算结果均保留两位有效数字)
(1)氧气的摩尔质量;
(2)标准状况下氧气分子间的平均距离;
(3)标准状况下1 cm3的氧气中含有的氧气分子数。
答案 (1)3.2×10-2 kg/mol (2)3.3×10-9 m (3)2.7×1019个
(1)氧气的摩尔质量为
M=NAm0=6.02×1023×5.3×10-26 kg/mol≈3.2×10-2 kg/mol;
而每个氧气分子占有的体积可以看成是棱长为a的立方体,
(3) 1 cm3氧气的质量为
m=ρV=1.43×1×10-6 kg=1.43×10-6 kg
则1 cm3氧气中含有的氧气分子数
5.地球到月球的平均距离为3.8×105 km。已知铁的摩尔质量为5.6×10-2 kg/
mol,密度为7.9×103 kg/m3,阿伏伽德罗常数NA=6.02×1023 mol-1。若把铁原子一个紧挨一个地单列排起来,筑成从地球通往月球的“原子大道”。求:(π=3.14,计算结果保留三位有效数字)
(1)这条“原子大道”共需多少个铁原子?
(2)这条“原子大道”的质量为多少?
答案 (1)1.35×1018个 (2)1.26×10-7 kg
(1)铁原子为球形,设直径为d,
“原子大道”的铁原子数
(2)“原子大道”的质量
分子动理论的基本内容(一)
目标一
阿伏加德罗常数
1. 阿伏加德罗常数NA=6.02×1023 mol-1
2.微观量与宏观量的桥梁
1.球体模型(固体、液体)
2.立方体模型(气体)
目标二
两种分子模型
幽默一笑
闻到屎味,就意味着吸入屎分子嘛???
最精密的机器-光刻机
同课章节目录
- 第1章 分子动理论与气体实验定律
- 第1节 分子动理论的基本观点
- 第2节 科学测量:用油膜法估测油酸分子的大小
- 第3节 气体分子速率分布的统计规律
- 第4节 科学探究:气体压强与体积的关系
- 第5节 气体实验定律
- 第2章 固体与液体
- 第1节 固体类型及微观结构
- 第2节 表面张力和毛细现象
- 第3节 材料及其应用
- 第3章 热力学定律
- 第1节 热力学第一定律
- 第2节 能量的转化与守恒
- 第3节 热力学第二定律
- 第4节 熵——系统无序程度的量度
- 第4章 原子结构
- 第1节 电子的发现与汤姆孙原子模型
- 第2节 原子的核式结构模型
- 第3节 光谱与氢原子光谱
- 第4节 玻尔原子模型
- 第5章 原子核与核能
- 第1节 认识原子核
- 第2节 原子核衰变及半衰期
- 第3节 核力与核能
- 第4节 核裂变和核聚变
- 第5节 核能的利用与环境保护
- 第6章 波粒二象性
- 第1节 光电效应及其解释
- 第2节 实物粒子的波粒二象性
