10.4线段的垂直平分线 自主提升训练(含答案)鲁教版(五四制)七年级数学下册
文档属性
| 名称 | 10.4线段的垂直平分线 自主提升训练(含答案)鲁教版(五四制)七年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 242.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-19 00:22:10 | ||
图片预览


文档简介
鲁教版(五四学制)七年级数学下册《10.4线段的垂直平分线》
自主提升训练题
一.选择题
1.如图,已知△ABC中,DE、FG分别是AB,AC边上的垂直平分线,∠BAC=100°,AB>AC,则∠EAG的度数是( )
A.10° B.20° C.30° D.40°
2.如图,△ABC中,DE垂直平分AC,交AC于E,交BC于D,连接AD,AE=4cm,则△ABC的周长与△ABD的周长差为( )
A.2cm B.4cm C.6cm D.8cm
3.如图,△ABC中,DE垂直平分边AC,若BC=8,AB=10,则△EBC的周长为( )
A.16 B.18 C.26 D.28
4.如图,在△ABC中,AC的垂直平分线分别交AC、BC于E、D两点,△ABC的周长为23,△ABD的周长为15,则AC的长是( )
A.6 B.8 C.12 D.16
二.填空题
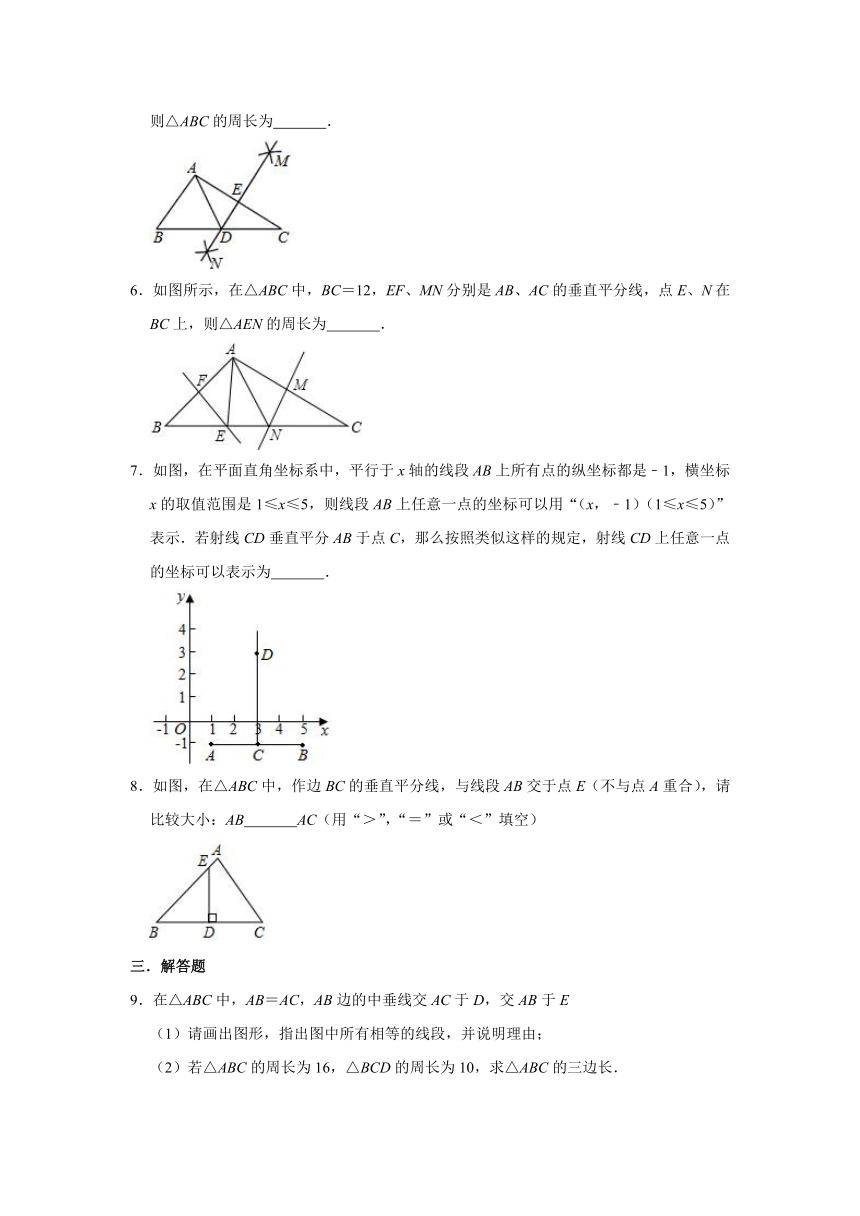
5.如图,在△ABC中,分别以点A和点C为圆心,大于AC长为半径画弧,两弧相交于点M、N;作直线MN分别交BC、AC于点D、点E,若AE=3cm,△ABD的周长为13cm,则△ABC的周长为 .
6.如图所示,在△ABC中,BC=12,EF、MN分别是AB、AC的垂直平分线,点E、N在BC上,则△AEN的周长为 .
7.如图,在平面直角坐标系中,平行于x轴的线段AB上所有点的纵坐标都是﹣1,横坐标x的取值范围是1≤x≤5,则线段AB上任意一点的坐标可以用“(x,﹣1)(1≤x≤5)”表示.若射线CD垂直平分AB于点C,那么按照类似这样的规定,射线CD上任意一点的坐标可以表示为 .
8.如图,在△ABC中,作边BC的垂直平分线,与线段AB交于点E(不与点A重合),请比较大小:AB AC(用“>”,“=”或“<”填空)
三.解答题
9.在△ABC中,AB=AC,AB边的中垂线交AC于D,交AB于E
(1)请画出图形,指出图中所有相等的线段,并说明理由;
(2)若△ABC的周长为16,△BCD的周长为10,求△ABC的三边长.
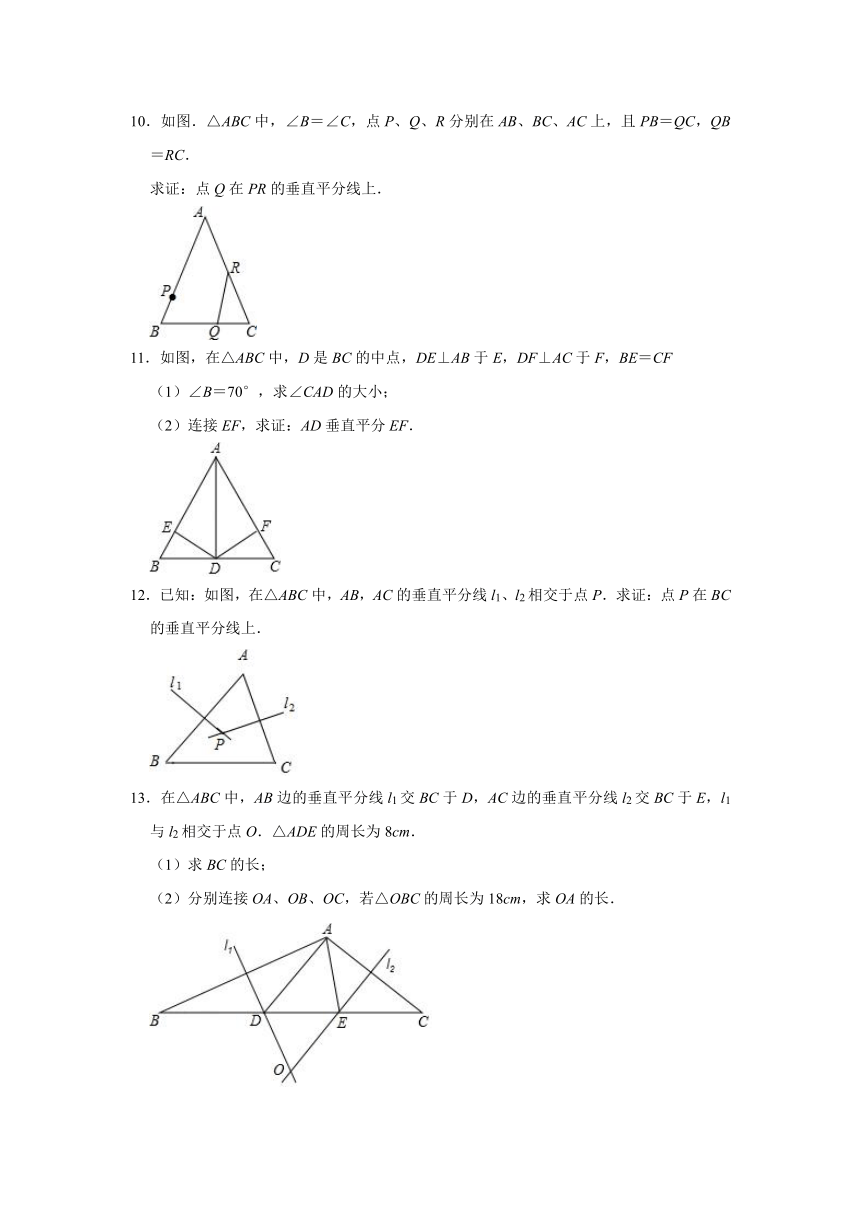
10.如图.△ABC中,∠B=∠C,点P、Q、R分别在AB、BC、AC上,且PB=QC,QB=RC.
求证:点Q在PR的垂直平分线上.
11.如图,在△ABC中,D是BC的中点,DE⊥AB于E,DF⊥AC于F,BE=CF
(1)∠B=70°,求∠CAD的大小;
(2)连接EF,求证:AD垂直平分EF.
12.已知:如图,在△ABC中,AB,AC的垂直平分线l1、l2相交于点P.求证:点P在BC的垂直平分线上.
13.在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O.△ADE的周长为8cm.
(1)求BC的长;
(2)分别连接OA、OB、OC,若△OBC的周长为18cm,求OA的长.
14.如图,已知AB比AC长2cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是14cm,求AB和AC的长.
15.如图,MN是线段AD的垂直平分线,BD交MN于C,点E在MN上,连接AC、AE、BE.求证:AC+BC<AE+BE.(提示:连接DE)
16.敌军基地在三条公路围成的三角区域内,我军一队战士在一条公路中点垂直射击,另一队战士在另一条公路中点垂直射击,均击中敌军基地,问第三队战士在公路何处垂直射击可击中目标?
17.在△ABC中,AD是高,在线段DC上取一点E,使BD=DE,已知AB+BD=DC,
求证:E点在线段AC的垂直平分线上.
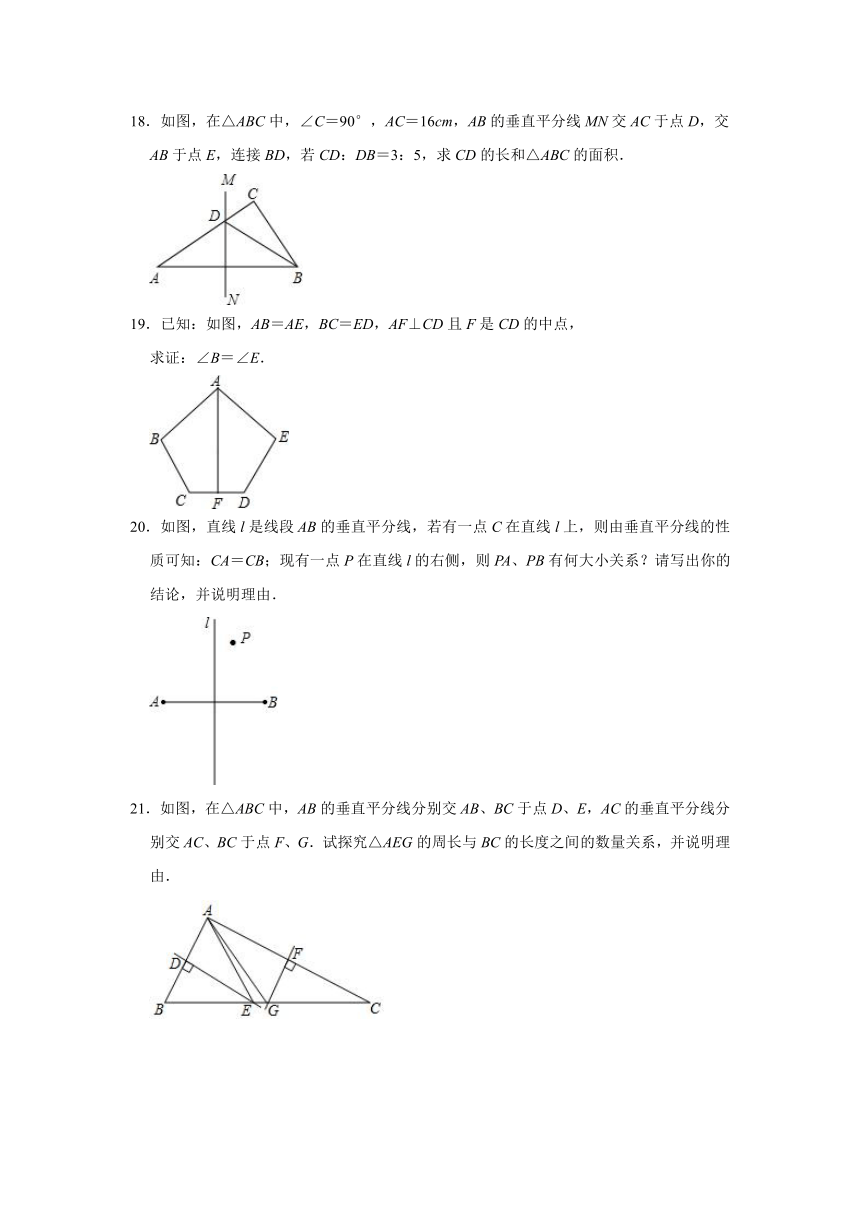
18.如图,在△ABC中,∠C=90°,AC=16cm,AB的垂直平分线MN交AC于点D,交AB于点E,连接BD,若CD:DB=3:5,求CD的长和△ABC的面积.
19.已知:如图,AB=AE,BC=ED,AF⊥CD且F是CD的中点,
求证:∠B=∠E.
20.如图,直线l是线段AB的垂直平分线,若有一点C在直线l上,则由垂直平分线的性质可知:CA=CB;现有一点P在直线l的右侧,则PA、PB有何大小关系?请写出你的结论,并说明理由.
21.如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G.试探究△AEG的周长与BC的长度之间的数量关系,并说明理由.
22.如图,在等腰△ABC中,AB=AC=20,DE垂直平分AB.
(1)若△BCE的周长为35,求BC的长;
(2)若BC=13,求△BCE的周长.
23.如图,在△ABC中,∠C=90°,用直尺和圆规作BC的垂直平分线l,交斜边AB于点O.
(1)猜想:点O是AB的什么特殊点?证明你的猜想;
(2)点O在AC的垂直平分线上吗?说明理由;
(3)结合(1)(2),你有何发现?
参考答案
一.选择题
1.解:∵BAC=100°,
∴∠B+∠C=80°,
∵DE是AB边上的垂直平分线,
∴DA=DB,
∴∠DAB=∠B,
同理,∠GAC=∠C,
∴∠DAB+∠GAC=∠B+∠C=80°,
∴∠DAG=∠BAC﹣(∠DAB+∠GAC)=20°,
故选:B.
2.解:∵DE垂直平分边AC,AE=4cm,
∴AD=CD,AC=2AE=8cm,
∵△ABC的周长=AB+AC+BC,
∵△ABD的周长=AB+AD+BD=AB+BC,
∴△ABC的周长与△ABD的周长差AC=8cm.
故选:D.
3.解:∵DE是△ABC中AC边的垂直平分线,
∴EA=EC,
∴△EBC的周长=BC+BE+EC=BC+BE+EA=BC+BA=18,
故选:B.
4.解:∵AC的垂直平分线分别交AC、BC于E、D两点,
∴AD=CD,
∵△ABC的周长为23,△ABD的周长为15,
∴AB+AC+BC=23,AB+BD+AD=15,
∴AB+BD+AD=AB+BD+CD=AB+BC=15,
∴AC=23﹣15=8,
故选:B.
二.填空题
5.解:由尺规作图可知,MN是线段AC的垂直平分线,
∴DA=DC,AC=2AE=6,
∵△ABD的周长为13,
∴AB+AD+BD=AB+DC+BD=AB+BC=13,
则△ABC的周长=AB+BC+AC=13+6=19(cm),
故答案为:19cm.
6.解:∵EF、MN分别是AB、AC的垂直平分线,
∴EA=EB,NA=NC,
∴△AEN的周长=AE+EN+NA=BE+EN+NC=BC=12,
故答案为:12.
7.解:∵点A的坐标为(1,﹣1),点B的坐标为(5,﹣1),C是AB的中点,
∴点C的坐标为(3,﹣1),
∴线CD上任意一点的坐标可以表示为:(3,y)(y≥﹣1),
故答案为:(3,y)(y≥﹣1).
8.解:连接EC,
∵ED是边BC的垂直平分线,
∴EB=EC,
在△AEC中,AE+EC>AC,
∴AE+EB>AC,即AB>AC,
故答案为:>.
三.解答题
9.解:(1)∵DE是AB边的中垂线,
∴DA=DB,AE=BE;
(2)△BCD的周长=BC+CD+DB=BC+AC=10,
△ABC的周长=BC+AC+AB=16,
∴AB=6,
则AC=AB=6,BC=4.
10.证明:连接PQ,
在△BQP和△CRQ中,
,
∴△BQP≌△CRQ,
∴QP=QR,
∴点Q在PR的垂直平分线上.
11.(1)解:∵D是BC的中点,
∴DB=DC,
在Rt△BDE和Rt△CDF中,
,
∴Rt△BDE≌Rt△CDF(HL)
∴DE=DF,∠C=∠B=70°,
∴∠BAC=40°,
∵DE=DF,DE⊥AB,DF⊥AC,
∴∠CAD=∠BAC=20°;
(2)证明:∵∠C=∠B,
∴AB=AC,
∵BE=CF,
∴AE=AF,又DE=DF,
∴AD垂直平分EF.
12.证明:连接PA、PB、PC,
∵l1是AB的垂直平分线,
∴PA=PB,
∵l2是AC的垂直平分线,
∴PA=PC,
∴PB=PC,
∴点P在BC的垂直平分线上.
13.解:(1)∵DO、EO分别是线段AB、AC的垂直平分线,
∴AD=BD,AE=CE,
∴AD+DE+AE=BD+DE+CE=BC,
∵△ADE的周长为8cm,
即AD+DE+AE=8cm,
∴BC=8cm;
(2)∵AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,
∴OA=OC=OB,
∵△OBC的周长为18cm,
即OC+OB+BC=18cm,
∴OC+OB=18﹣8=10cm,
∴OC=5cm,
∴OA=OC=OB=5cm.
14.解:BC的垂直平分线交AB于点D,
∴DB=DC,
∵△ACD的周长是14,
∴AD+AC+CD=14,即AC+AB=14,
则,
解得,AB=8cm,AC=6cm.
15.证明:∵MN是线段AD的垂直平分线,
∴CA=CD,EA=ED,
在△BDE中,
DB<ED+BE,
即AC+BC<AE+BE.
16.解:第三队战士在第三条公路中点处垂直射击可击中目标,
∵一队战士在一条公路中点垂直射击,
∴敌军基地到这条公路与另两条公路交点的距离相等,
同理,敌军基地到第二条公路与另两条公路交点的距离相等,
∴敌军基地在第三条公路与另两条公路交点之间公路的垂直平分线上,
∴第三队战士在第三条公路中点处垂直射击可击中目标.
17.证明:∵AD是高,∴AD⊥BC,
又∵BD=DE,
∴AD所在的直线是线段BE的垂直平分线,
∴AB=AE,
∴AB+BD=AE+DE,
又∵AB+BD=DC,
∴DC=AE+DE,
∴DE+EC=AE+DE
∴EC=AE,
∴点E在线段AC的垂直平分线上.
18.解:∵CD:DB=3:5,
∴设DC=3x,BD=5x,
又∵MN是线段AB的垂直平分线,
∴AD=DB=5x,
又∵AC=16cm,
∴3x+5x=16,
解得,x=2,
∴CD=6cm,DB=10cm,
在Rt△BDC中,CD=6cm,DB=10cm,
∴△ABC的面积=.
答:CD的长为6cm,△ABC的面积为64cm2.
19.证明:连接AC,AD,
∵AF⊥CD,F为CD的中点,
∴AC=AD,
在△ABC和△AED中
,
∴△ABC≌△AED,
∴∠B=∠E.
20.解:PA>PB.理由如下:
如图,连接PA,与直线l交于点C;连接PB、BC.
因为直线l是线段AB的垂直平分线,
所以CA=CB;
因为三角形任意两边之和大于第三边,所以PC+CB>PB;
所以PC+CA>PB,即PA>PB.
21.解:△AEG的周长等于BC的长度,理由如下:
∵DE是AB的垂直平分线,
∴EA=EB.
∵FG是AC的垂直平分线,
∴GA=GC.
∴△AEG周长=AE+EG+AG=BE+EG+CG=BC.
22.解:(1)∵DE垂直平分AB,
∴EA=EB,
∵△BCE的周长=BC+CE+BE=BC+CE+EA=BC+AC=35,AB=AC=20,
∴BC=15;
(2)△BCE的周长=BC+CE+BE=BC+CE+EA=BC+AC=33.
23.解:(1)点O是AB的中点,
证明:∵OE是线段AB的垂直平分线,
∴OC=OB,
∴∠OCB=∠OBC,
∵∠OCB+∠OCA=90°,∠OBC+∠A=90°,
∴∠OCA=∠A,
∴OA=OC,又OC=OB,
∴OA=OB,
∴点O是AB的中点;
(2)∵OA=OC,
∴点O在AC的垂直平分线上;
(3)结合(1)(2)可知,直角三角形三边的垂直平分线相交于斜边的中点.
自主提升训练题
一.选择题
1.如图,已知△ABC中,DE、FG分别是AB,AC边上的垂直平分线,∠BAC=100°,AB>AC,则∠EAG的度数是( )
A.10° B.20° C.30° D.40°
2.如图,△ABC中,DE垂直平分AC,交AC于E,交BC于D,连接AD,AE=4cm,则△ABC的周长与△ABD的周长差为( )
A.2cm B.4cm C.6cm D.8cm
3.如图,△ABC中,DE垂直平分边AC,若BC=8,AB=10,则△EBC的周长为( )
A.16 B.18 C.26 D.28
4.如图,在△ABC中,AC的垂直平分线分别交AC、BC于E、D两点,△ABC的周长为23,△ABD的周长为15,则AC的长是( )
A.6 B.8 C.12 D.16
二.填空题
5.如图,在△ABC中,分别以点A和点C为圆心,大于AC长为半径画弧,两弧相交于点M、N;作直线MN分别交BC、AC于点D、点E,若AE=3cm,△ABD的周长为13cm,则△ABC的周长为 .
6.如图所示,在△ABC中,BC=12,EF、MN分别是AB、AC的垂直平分线,点E、N在BC上,则△AEN的周长为 .
7.如图,在平面直角坐标系中,平行于x轴的线段AB上所有点的纵坐标都是﹣1,横坐标x的取值范围是1≤x≤5,则线段AB上任意一点的坐标可以用“(x,﹣1)(1≤x≤5)”表示.若射线CD垂直平分AB于点C,那么按照类似这样的规定,射线CD上任意一点的坐标可以表示为 .
8.如图,在△ABC中,作边BC的垂直平分线,与线段AB交于点E(不与点A重合),请比较大小:AB AC(用“>”,“=”或“<”填空)
三.解答题
9.在△ABC中,AB=AC,AB边的中垂线交AC于D,交AB于E
(1)请画出图形,指出图中所有相等的线段,并说明理由;
(2)若△ABC的周长为16,△BCD的周长为10,求△ABC的三边长.
10.如图.△ABC中,∠B=∠C,点P、Q、R分别在AB、BC、AC上,且PB=QC,QB=RC.
求证:点Q在PR的垂直平分线上.
11.如图,在△ABC中,D是BC的中点,DE⊥AB于E,DF⊥AC于F,BE=CF
(1)∠B=70°,求∠CAD的大小;
(2)连接EF,求证:AD垂直平分EF.
12.已知:如图,在△ABC中,AB,AC的垂直平分线l1、l2相交于点P.求证:点P在BC的垂直平分线上.
13.在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O.△ADE的周长为8cm.
(1)求BC的长;
(2)分别连接OA、OB、OC,若△OBC的周长为18cm,求OA的长.
14.如图,已知AB比AC长2cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是14cm,求AB和AC的长.
15.如图,MN是线段AD的垂直平分线,BD交MN于C,点E在MN上,连接AC、AE、BE.求证:AC+BC<AE+BE.(提示:连接DE)
16.敌军基地在三条公路围成的三角区域内,我军一队战士在一条公路中点垂直射击,另一队战士在另一条公路中点垂直射击,均击中敌军基地,问第三队战士在公路何处垂直射击可击中目标?
17.在△ABC中,AD是高,在线段DC上取一点E,使BD=DE,已知AB+BD=DC,
求证:E点在线段AC的垂直平分线上.
18.如图,在△ABC中,∠C=90°,AC=16cm,AB的垂直平分线MN交AC于点D,交AB于点E,连接BD,若CD:DB=3:5,求CD的长和△ABC的面积.
19.已知:如图,AB=AE,BC=ED,AF⊥CD且F是CD的中点,
求证:∠B=∠E.
20.如图,直线l是线段AB的垂直平分线,若有一点C在直线l上,则由垂直平分线的性质可知:CA=CB;现有一点P在直线l的右侧,则PA、PB有何大小关系?请写出你的结论,并说明理由.
21.如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G.试探究△AEG的周长与BC的长度之间的数量关系,并说明理由.
22.如图,在等腰△ABC中,AB=AC=20,DE垂直平分AB.
(1)若△BCE的周长为35,求BC的长;
(2)若BC=13,求△BCE的周长.
23.如图,在△ABC中,∠C=90°,用直尺和圆规作BC的垂直平分线l,交斜边AB于点O.
(1)猜想:点O是AB的什么特殊点?证明你的猜想;
(2)点O在AC的垂直平分线上吗?说明理由;
(3)结合(1)(2),你有何发现?
参考答案
一.选择题
1.解:∵BAC=100°,
∴∠B+∠C=80°,
∵DE是AB边上的垂直平分线,
∴DA=DB,
∴∠DAB=∠B,
同理,∠GAC=∠C,
∴∠DAB+∠GAC=∠B+∠C=80°,
∴∠DAG=∠BAC﹣(∠DAB+∠GAC)=20°,
故选:B.
2.解:∵DE垂直平分边AC,AE=4cm,
∴AD=CD,AC=2AE=8cm,
∵△ABC的周长=AB+AC+BC,
∵△ABD的周长=AB+AD+BD=AB+BC,
∴△ABC的周长与△ABD的周长差AC=8cm.
故选:D.
3.解:∵DE是△ABC中AC边的垂直平分线,
∴EA=EC,
∴△EBC的周长=BC+BE+EC=BC+BE+EA=BC+BA=18,
故选:B.
4.解:∵AC的垂直平分线分别交AC、BC于E、D两点,
∴AD=CD,
∵△ABC的周长为23,△ABD的周长为15,
∴AB+AC+BC=23,AB+BD+AD=15,
∴AB+BD+AD=AB+BD+CD=AB+BC=15,
∴AC=23﹣15=8,
故选:B.
二.填空题
5.解:由尺规作图可知,MN是线段AC的垂直平分线,
∴DA=DC,AC=2AE=6,
∵△ABD的周长为13,
∴AB+AD+BD=AB+DC+BD=AB+BC=13,
则△ABC的周长=AB+BC+AC=13+6=19(cm),
故答案为:19cm.
6.解:∵EF、MN分别是AB、AC的垂直平分线,
∴EA=EB,NA=NC,
∴△AEN的周长=AE+EN+NA=BE+EN+NC=BC=12,
故答案为:12.
7.解:∵点A的坐标为(1,﹣1),点B的坐标为(5,﹣1),C是AB的中点,
∴点C的坐标为(3,﹣1),
∴线CD上任意一点的坐标可以表示为:(3,y)(y≥﹣1),
故答案为:(3,y)(y≥﹣1).
8.解:连接EC,
∵ED是边BC的垂直平分线,
∴EB=EC,
在△AEC中,AE+EC>AC,
∴AE+EB>AC,即AB>AC,
故答案为:>.
三.解答题
9.解:(1)∵DE是AB边的中垂线,
∴DA=DB,AE=BE;
(2)△BCD的周长=BC+CD+DB=BC+AC=10,
△ABC的周长=BC+AC+AB=16,
∴AB=6,
则AC=AB=6,BC=4.
10.证明:连接PQ,
在△BQP和△CRQ中,
,
∴△BQP≌△CRQ,
∴QP=QR,
∴点Q在PR的垂直平分线上.
11.(1)解:∵D是BC的中点,
∴DB=DC,
在Rt△BDE和Rt△CDF中,
,
∴Rt△BDE≌Rt△CDF(HL)
∴DE=DF,∠C=∠B=70°,
∴∠BAC=40°,
∵DE=DF,DE⊥AB,DF⊥AC,
∴∠CAD=∠BAC=20°;
(2)证明:∵∠C=∠B,
∴AB=AC,
∵BE=CF,
∴AE=AF,又DE=DF,
∴AD垂直平分EF.
12.证明:连接PA、PB、PC,
∵l1是AB的垂直平分线,
∴PA=PB,
∵l2是AC的垂直平分线,
∴PA=PC,
∴PB=PC,
∴点P在BC的垂直平分线上.
13.解:(1)∵DO、EO分别是线段AB、AC的垂直平分线,
∴AD=BD,AE=CE,
∴AD+DE+AE=BD+DE+CE=BC,
∵△ADE的周长为8cm,
即AD+DE+AE=8cm,
∴BC=8cm;
(2)∵AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,
∴OA=OC=OB,
∵△OBC的周长为18cm,
即OC+OB+BC=18cm,
∴OC+OB=18﹣8=10cm,
∴OC=5cm,
∴OA=OC=OB=5cm.
14.解:BC的垂直平分线交AB于点D,
∴DB=DC,
∵△ACD的周长是14,
∴AD+AC+CD=14,即AC+AB=14,
则,
解得,AB=8cm,AC=6cm.
15.证明:∵MN是线段AD的垂直平分线,
∴CA=CD,EA=ED,
在△BDE中,
DB<ED+BE,
即AC+BC<AE+BE.
16.解:第三队战士在第三条公路中点处垂直射击可击中目标,
∵一队战士在一条公路中点垂直射击,
∴敌军基地到这条公路与另两条公路交点的距离相等,
同理,敌军基地到第二条公路与另两条公路交点的距离相等,
∴敌军基地在第三条公路与另两条公路交点之间公路的垂直平分线上,
∴第三队战士在第三条公路中点处垂直射击可击中目标.
17.证明:∵AD是高,∴AD⊥BC,
又∵BD=DE,
∴AD所在的直线是线段BE的垂直平分线,
∴AB=AE,
∴AB+BD=AE+DE,
又∵AB+BD=DC,
∴DC=AE+DE,
∴DE+EC=AE+DE
∴EC=AE,
∴点E在线段AC的垂直平分线上.
18.解:∵CD:DB=3:5,
∴设DC=3x,BD=5x,
又∵MN是线段AB的垂直平分线,
∴AD=DB=5x,
又∵AC=16cm,
∴3x+5x=16,
解得,x=2,
∴CD=6cm,DB=10cm,
在Rt△BDC中,CD=6cm,DB=10cm,
∴△ABC的面积=.
答:CD的长为6cm,△ABC的面积为64cm2.
19.证明:连接AC,AD,
∵AF⊥CD,F为CD的中点,
∴AC=AD,
在△ABC和△AED中
,
∴△ABC≌△AED,
∴∠B=∠E.
20.解:PA>PB.理由如下:
如图,连接PA,与直线l交于点C;连接PB、BC.
因为直线l是线段AB的垂直平分线,
所以CA=CB;
因为三角形任意两边之和大于第三边,所以PC+CB>PB;
所以PC+CA>PB,即PA>PB.
21.解:△AEG的周长等于BC的长度,理由如下:
∵DE是AB的垂直平分线,
∴EA=EB.
∵FG是AC的垂直平分线,
∴GA=GC.
∴△AEG周长=AE+EG+AG=BE+EG+CG=BC.
22.解:(1)∵DE垂直平分AB,
∴EA=EB,
∵△BCE的周长=BC+CE+BE=BC+CE+EA=BC+AC=35,AB=AC=20,
∴BC=15;
(2)△BCE的周长=BC+CE+BE=BC+CE+EA=BC+AC=33.
23.解:(1)点O是AB的中点,
证明:∵OE是线段AB的垂直平分线,
∴OC=OB,
∴∠OCB=∠OBC,
∵∠OCB+∠OCA=90°,∠OBC+∠A=90°,
∴∠OCA=∠A,
∴OA=OC,又OC=OB,
∴OA=OB,
∴点O是AB的中点;
(2)∵OA=OC,
∴点O在AC的垂直平分线上;
(3)结合(1)(2)可知,直角三角形三边的垂直平分线相交于斜边的中点.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
