10.3平行线的性质 自主提升训练题(含答案)沪科版七年级数学下册
文档属性
| 名称 | 10.3平行线的性质 自主提升训练题(含答案)沪科版七年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 264.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-19 00:24:27 | ||
图片预览

文档简介
沪科版七年级数学下册《10.3平行线的性质》自主提升训练题
1.如图,已知长方形纸片ABCD,点E,H在AD边上,点F,G在BC边上,分别沿EF,GH折叠,使点B和点C都落在点P处,若∠FEH+∠EHG=118°,则∠FPG的度数为( )
A.54° B.55° C.56° D.57°
2.如图,将一块长方形纸条折成如图的形状,若已知∠1=α,则∠2的度数为( )
A.90°﹣α B.90°+α C.90°﹣ D.90°+
3.AF是∠BAC的平分线,DF∥AC,若∠BAC=70°,则∠1的度数为( )
A.175° B.35° C.55° D.70°
4.将一副三角板(∠A=30°)按如图所示方式摆放,使得AB∥EF,则∠1等于( )
A.75° B.90° C.105° D.115°
5.同一平面内的三条直线a,b,c,若a⊥b,b∥c,则a与c( )
A.平行 B.垂直
C.相交但不垂直 D.重合
6.如图,直线l1∥l2,∠1=30°,则∠2+∠3=( )
A.150° B.180° C.210° D.240°
7.如图,∠BCD=90°,AB∥DE,则α与β一定满足的等式是( )
A.α+β=180° B.α+β=90° C.β=3α D.α﹣β=90°
8.如图,AC∥BE,∠ABE=70°,则∠A的度数为( )
A.70° B.65° C.50° D.140°
9.下列说法正确的是( )
A.同旁内角互补
B.相等的角是对顶角
C.从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离
D.经过直线外一点,有且只有一条直线与已知直线平行
10.如图,由AB∥DC,能推出正确的结论是( )
A.∠3=∠4 B.∠1=∠2 C.∠A=∠C D.AD∥BC
11.将一把直尺与一把三角板如图那样放置,若∠1=35°,∠2的度数是( )
A.65° B.70° C.75° D.80°
12.如图,若m∥n,∠1=105°,则∠2=( )
A.75° B.85° C.95° D.105°
13.如图,AB∥CD,CE平分∠BCD,∠DCE=18°,则∠B等于( )
A.18° B.36° C.45° D.54°
14.下列图形中,由AB∥CD,能得到∠1=∠2的是( )
A. B.
C. D.
15.已知:直线l1∥l2,一块含30°角的直角三角板如图所示放置,∠1=25°,则∠2等于( )
A.30° B.35° C.40° D.45°
16.如图,∠1=80°,a∥b,则∠2的度数是( )
A.100° B.70° C.80° D.60°
17.如图,CE是∠ACD的平分线,CD∥AB,DE⊥CE.若∠DEB=32°,则∠A的度数为 .
18.如图,四边形ABCD的长条形纸带,AB∥CD,将长方形沿EF折叠,A、D分别于A′、D′对应,若∠CFE=2∠CFD',则∠AEF的度数是 .
19.如图,将一张长方形纸条沿某条直线折叠,若∠1=118°,则∠2等于 .
20.把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=49°,则∠2﹣∠1= .
21.如图,AB∥CD,BE⊥EF于E,∠B=25°,则∠EFD的度数是 .
22.如图,已知AE∥BD,∠1=3∠2,∠2=28°.求∠C= .
23.如图,已知AB∥CD,∠1=100°,∠2=120°,则∠α= 度.
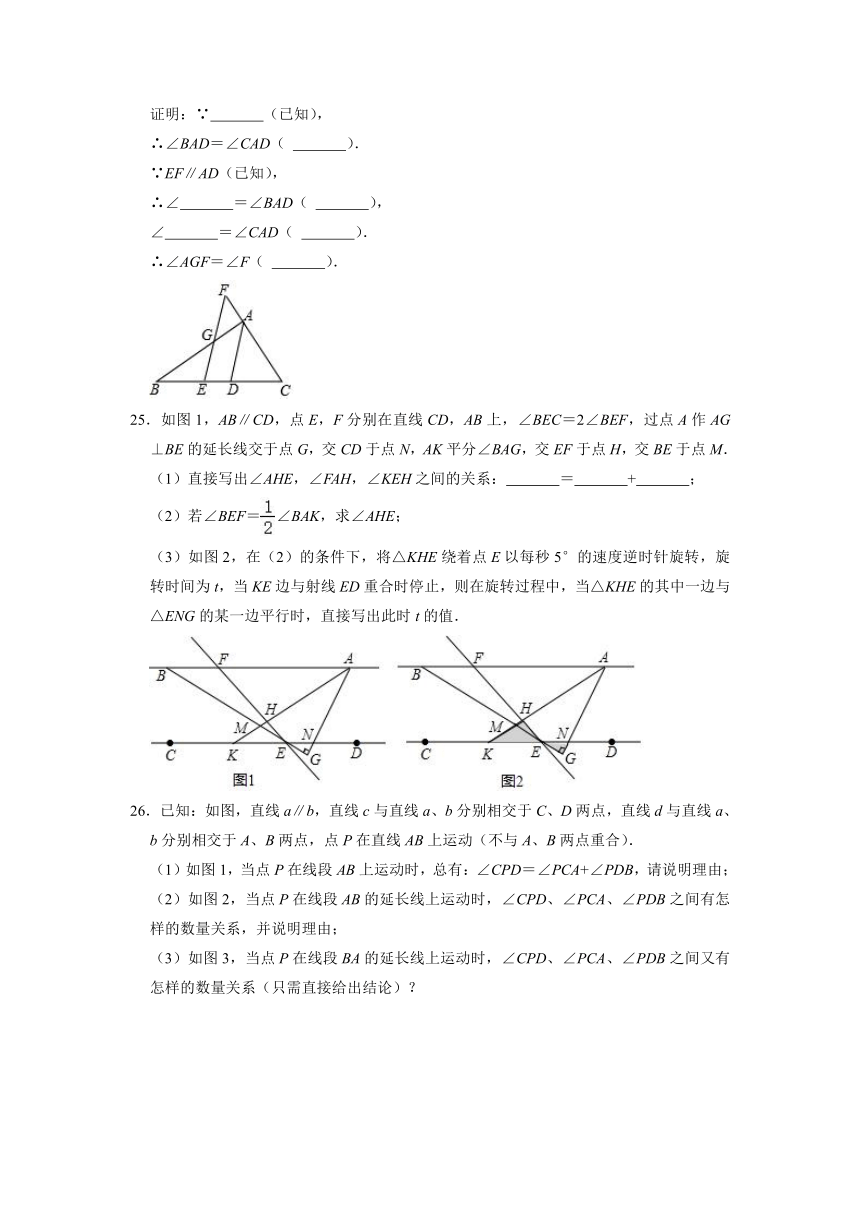
24.已知:如图,AD是∠BAC的平分线,点E在BC上,点F在CA的延长线上,EF∥AD,EF交AB于点G.
求证:∠AGF=∠F.
请你根据已知条件补充推理过程,并在相应括号内注明理由.
证明:∵ (已知),
∴∠BAD=∠CAD( ).
∵EF∥AD(已知),
∴∠ =∠BAD( ),
∠ =∠CAD( ).
∴∠AGF=∠F( ).
25.如图1,AB∥CD,点E,F分别在直线CD,AB上,∠BEC=2∠BEF,过点A作AG⊥BE的延长线交于点G,交CD于点N,AK平分∠BAG,交EF于点H,交BE于点M.
(1)直接写出∠AHE,∠FAH,∠KEH之间的关系: = + ;
(2)若∠BEF=∠BAK,求∠AHE;
(3)如图2,在(2)的条件下,将△KHE绕着点E以每秒5°的速度逆时针旋转,旋转时间为t,当KE边与射线ED重合时停止,则在旋转过程中,当△KHE的其中一边与△ENG的某一边平行时,直接写出此时t的值.
26.已知:如图,直线a∥b,直线c与直线a、b分别相交于C、D两点,直线d与直线a、b分别相交于A、B两点,点P在直线AB上运动(不与A、B两点重合).
(1)如图1,当点P在线段AB上运动时,总有:∠CPD=∠PCA+∠PDB,请说明理由;
(2)如图2,当点P在线段AB的延长线上运动时,∠CPD、∠PCA、∠PDB之间有怎样的数量关系,并说明理由;
(3)如图3,当点P在线段BA的延长线上运动时,∠CPD、∠PCA、∠PDB之间又有怎样的数量关系(只需直接给出结论)?
27.根据图形及题意填空,并在括号里写上理由.
已知:如图,AD∥BC,AD平分∠EAC.
试说明:∠B=∠C
解:∵AD平分∠EAC(已知)
∴∠1=∠2(角平分线的定义)
∵AD∥BC(已知)
∴∠ =∠ ( )
∠ =∠ ( )
∴∠B=∠C.
参考答案
1.解:∵四边形ABCD是长方形,
∴AD∥BC,
∴∠FEH=∠BFE,∠EHG=∠CGH,
∴∠BFE+∠CGH=∠FEH+∠EHG=118°,
由折叠可知:
EF,GH分别是∠BFP和∠CGP的角平分线,
∴∠PFE=∠BFE,∠PGH=∠CGH,
∴∠PFE+∠PGH=∠BFE+∠CGH=118°,
∴∠BFP+∠CGP=2(∠BFE+∠CGH)=236°,
∴∠PFG+∠PGF=360°﹣(∠BFP+∠CGP)=360°﹣236°=124°,
∴∠FPG=180°﹣(∠PFG+∠PGF)=180°﹣124°=56°.
故选:C.
2.解:如图,标出字母,
∵AB∥CD,
∴∠1+∠FBC+∠2=180°,
∵纸条是对折,
∴∠FBC=∠2,
∴2∠2+∠1=180°,
∵∠1=α,
∴∠2=×(180°﹣α),
∴∠2=90°﹣α,
故选:C.
3.解:∵∠BAC=70°,AF平分∠BAC,
∴∠FAC=∠BAC=35°,
∵DF∥AC,
∴∠1=∠FAC=35°,
故选:B.
4.解:∵AB∥EF,
∴∠BDE=∠E=45°,
又∵∠A=30°,
∴∠B=60°,
∴∠1=∠BDE+∠B=45°+60°=105°,
故选:C.
5.解:如图所示:
∵b∥c,
∴∠1=∠2,
又∵a⊥b,
∴∠1=90°,
∴∠1=∠2=90°,
即a⊥c.
故选:B.
解:过点E作EF∥11,
∵11∥12,EF∥11,
∴EF∥11∥12,
∴∠1=∠AEF=30°,∠FEC+∠3=180°,
∴∠2+∠3=∠AEF+∠FEC+∠3=30°+180°=210°,
故选:C.
7.解:过C作CF∥AB,
∵AB∥DE,
∴AB∥DE∥CF,
∴∠1=∠β,∠α=180°﹣∠2,
∴∠α﹣∠β=180°﹣∠2﹣∠1=180°﹣∠BCD=90°,
故选:D.
8.解:∵AC∥BE,
∴∠A=∠ABE=70°,
故选:A.
9.解:A、两直线平行,同旁内角才互补,故本选项错误;
B、相等的角位置关系不固定,对顶角是其中一种,故本选项错误;
C、距离是一段长度,用具体数值表示,从直线外一点到这条直线的垂线段的长度,叫做这点到这条直线的距离,故本选项错误;
D、经过直线外一点,有且只有一条直线与已知直线平行,故本选项正确.
故选:D.
10.解:A、中的两个角不是由两平行线AB和CD形成的内错角,故无法判断两角的数量关系,故错误;
B、∵AB∥DC,∠1和∠2互为内错角,∴∠1=∠2,故正确.
C、∵AB∥CD,∴∠C+∠ABC=180°;∵直线AD与BC的位置关系不确定,∴∠A与∠ABC的数量关系无法确定,∴∠A与∠C的关系无法确定,故错误;
D、由题意知,直线AD与BC的位置关系不确定,故错误.
故选:B.
11.解:∵直尺的两边互相平行,∠1=35°,
∴∠3=∠1=35°,
∴∠2=35°+30°=65°.
故选:A.
12.解:∵m∥n,∠1=105°,
∴∠2=180°﹣∠1=180°﹣105°=75°.
故选:A.
13.解:∵CE平分∠BCD,∠DCE=18°,
∴∠BCD=2∠DCE=2×18°=36°,
∵AB∥CD,
∴∠B=∠BCD=36°.
故选:B.
14.解:A、∵AB∥CD,
∴∠1+∠2=180°,
故A错误;
B、∵AB∥CD,
∴∠1=∠3,
∵∠2=∠3,
∴∠1=∠2,
故B正确;
C、∵AB∥CD,
∴∠BAD=∠CDA,
若AC∥BD,可得∠1=∠2;
故C错误;
D、若梯形ABCD是等腰梯形,可得∠1=∠2,
故D错误.
故选:B.
15.解:∵∠3是△ADG的外角,
∴∠3=∠A+∠1=30°+25°=55°,
∵l1∥l2,
∴∠3=∠4=55°,
∵∠4+∠EFC=90°,
∴∠EFC=90°﹣55°=35°,
∴∠2=35°.
故选:B.
16.解:∵∠1=80°,a∥b,
∴∠3=∠1=80°,
∴∠2=∠3=80°.
故选:C.
17.解:∵DE⊥CE,
∴∠CED=90°,
∵∠AEC+∠CED+∠DEB=180°,∠DEB=32°,
∴∠AEC=180°﹣∠CED﹣∠DEB=180°﹣90°﹣32°=58°,
∵CD∥AB,
∴∠DCE=∠AEC=58°,
∵CE是∠ACD的平分线,
∴∠ACD=2∠ACE=2×58°=116°,
∴∠ACE=∠AEC,
∵CD∥AB,
∴∠A+∠ACD=180°,
∴∠A=180°﹣∠ACD=180°﹣116°=64°.
故答案为:64°.
18.解:∵AB∥CD,
∴∠CFE=∠AEF,
又∵∠DFE=∠D′FE,∠CFE=2∠CFD′,
∴∠DFE=∠D′FE=3∠CFD′,
∴∠DFE+∠CFE=3∠CFD′+2∠CFD′=180°,
∴∠CFD′=36°,
∴∠AEF=∠CFE=2∠CFD′=72°.
故答案为:72°.
19.解:如图,∵AB∥CD,
∴∠1=∠BAC=118°,
由折叠可得,∠BAD=∠BAC=59°,
∵AB∥CD,
∴∠2=∠BAD=59°,
故答案为:59°.
20.解:∵AD∥BC,
∴∠2=∠DEG,∠EFG=∠DEF=49°,
∵长方形纸片ABCD沿EF折叠后ED与BC的交点为G,
∴∠DEF=∠GEF=49°,
∴∠2=2×49°=98°,
∴∠1=180°﹣98°=82°,
∴∠2﹣∠1=98°﹣82°=16°.
故答案为16°.
21.解:如图,
∵BE⊥EF,
∴∠E=90°,
∵∠B=25°,
∴∠1=65°,
∵AB∥CD,
∴∠EFD=∠1=65°.
故答案为:65°.
22.解:∵AE∥DB,
∴∠1=∠3=3∠2,
∵∠2+∠C=∠3,
∴∠2+∠C=3∠2,
∴∠C=2∠2,
∵∠2=28°.
∴∠C=56°,
故答案为:56°.
23.解:如图,过点F作EF∥AB,
∴∠1+∠3=180°.
∵∠1=100°,
∴∠3=80°.
∵AB∥CD,
∴CD∥EF,
∴∠4+∠2=180°,
∵∠2=120°,
∴∠4=60°.
∴∠α=180°﹣∠3﹣∠4=40°.
故应填40.
24.证明:∵AD是△ABC的角平分线(已知),
∴∠BAD=∠CAD(角平分线的定义),
∵EF∥AD(已知),
∴∠FGA=∠BAD(两直线平行,内错角相等),
∠F=∠CAD(两直线平行,同位角相等),
∴∠AGF=∠F(等量代换),
故答案为:AD是△ABC的角平分线;角平分线的定义;FGA,两直线平行,内错角相等;F,两直线平行,同位角相等;等量代换.
25.解:(1)∵AB∥CD
∴∠KEH=∠AFH
∵∠AHE=∠AFH+∠FAH
∴∠AHE=∠KEH+∠FAH
故答案为:∠AHE;∠KEH;∠FAH;
(2)设∠BEF=x
∵∠BEF=∠BAK,∠BEC=2∠BEF
∴∠BAK=∠BEC=2x
∵AK平分∠BAG
∴∠BAK=∠KAG=2x
由(1)的结论可得:∠AME=2x+2x=4x,∠AHE=2x+3x=5x
∵AG⊥BE
∴∠G=90°
∴∠AME+∠KAG=2x+4x=90°
∴x=15°
∴∠AHE=5x=75°;
(3)由(2)可得,∠KHE=105°,∠BEF=15°,∠HEK=45°,∠NEG=30°,∠ENG=60°
①当KH∥NG时
5°×t=60°﹣30°=30°
∴t=6
②当KE∥GN时
5°×t=60°
∴t=12
③当HE∥GN时
5°×t=45°+60°=105°
∴t=21
④当HK∥EG时,
5°×t=180°﹣30°﹣30°=120°
∴t=24
⑤当HK∥EN时,5t=150°
∴t=30
综上所述,t的值为:6或12或21或24或30.
26.解:(1)证明:如图1,过点P作PE∥a,则∠1=∠CPE.
∵a∥b,PE∥a,
∴PE∥b,
∴∠2=∠DPE,
∴∠3=∠1+∠2,
即∠CPD=∠PCA+∠PDB;
(2)∠CPD=∠PCA﹣∠PDB.
理由:如图2,过点P作PE∥b,则∠2=∠EPD,
∵直线a∥b,
∴a∥PE,
∴∠1=∠EPC,
∵∠3=∠EPC﹣∠EPD,
∴∠3=∠1﹣∠2,
即∠CPD=∠PCA﹣∠PDB;
(3)∠CPD=∠PDB﹣∠PCA.
证明:如图3,设直线AC与DP交于点F,
∵∠PFA是△PCF的外角,
∴∠PFA=∠1+∠3,
∵a∥b,
∴∠2=∠PFA,
∴∠2=∠1+∠3,
∴∠3=∠2﹣∠1,
即∠CPD=∠PDB﹣∠PCA.
27.解:∵AD平分∠EAC,(已知)
∴∠1=∠2,(角平分线的定义)
∵AD∥BC,(已知)
∴∠1=∠B,(两直线平行,同位角相等)
∠2=∠C,(两直线平行,内错角相等)
∴∠B=∠C.
故答案为:1;B;两直线平行,同位角相等;2;C;两直线平行,内错角相等.
1.如图,已知长方形纸片ABCD,点E,H在AD边上,点F,G在BC边上,分别沿EF,GH折叠,使点B和点C都落在点P处,若∠FEH+∠EHG=118°,则∠FPG的度数为( )
A.54° B.55° C.56° D.57°
2.如图,将一块长方形纸条折成如图的形状,若已知∠1=α,则∠2的度数为( )
A.90°﹣α B.90°+α C.90°﹣ D.90°+
3.AF是∠BAC的平分线,DF∥AC,若∠BAC=70°,则∠1的度数为( )
A.175° B.35° C.55° D.70°
4.将一副三角板(∠A=30°)按如图所示方式摆放,使得AB∥EF,则∠1等于( )
A.75° B.90° C.105° D.115°
5.同一平面内的三条直线a,b,c,若a⊥b,b∥c,则a与c( )
A.平行 B.垂直
C.相交但不垂直 D.重合
6.如图,直线l1∥l2,∠1=30°,则∠2+∠3=( )
A.150° B.180° C.210° D.240°
7.如图,∠BCD=90°,AB∥DE,则α与β一定满足的等式是( )
A.α+β=180° B.α+β=90° C.β=3α D.α﹣β=90°
8.如图,AC∥BE,∠ABE=70°,则∠A的度数为( )
A.70° B.65° C.50° D.140°
9.下列说法正确的是( )
A.同旁内角互补
B.相等的角是对顶角
C.从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离
D.经过直线外一点,有且只有一条直线与已知直线平行
10.如图,由AB∥DC,能推出正确的结论是( )
A.∠3=∠4 B.∠1=∠2 C.∠A=∠C D.AD∥BC
11.将一把直尺与一把三角板如图那样放置,若∠1=35°,∠2的度数是( )
A.65° B.70° C.75° D.80°
12.如图,若m∥n,∠1=105°,则∠2=( )
A.75° B.85° C.95° D.105°
13.如图,AB∥CD,CE平分∠BCD,∠DCE=18°,则∠B等于( )
A.18° B.36° C.45° D.54°
14.下列图形中,由AB∥CD,能得到∠1=∠2的是( )
A. B.
C. D.
15.已知:直线l1∥l2,一块含30°角的直角三角板如图所示放置,∠1=25°,则∠2等于( )
A.30° B.35° C.40° D.45°
16.如图,∠1=80°,a∥b,则∠2的度数是( )
A.100° B.70° C.80° D.60°
17.如图,CE是∠ACD的平分线,CD∥AB,DE⊥CE.若∠DEB=32°,则∠A的度数为 .
18.如图,四边形ABCD的长条形纸带,AB∥CD,将长方形沿EF折叠,A、D分别于A′、D′对应,若∠CFE=2∠CFD',则∠AEF的度数是 .
19.如图,将一张长方形纸条沿某条直线折叠,若∠1=118°,则∠2等于 .
20.把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=49°,则∠2﹣∠1= .
21.如图,AB∥CD,BE⊥EF于E,∠B=25°,则∠EFD的度数是 .
22.如图,已知AE∥BD,∠1=3∠2,∠2=28°.求∠C= .
23.如图,已知AB∥CD,∠1=100°,∠2=120°,则∠α= 度.
24.已知:如图,AD是∠BAC的平分线,点E在BC上,点F在CA的延长线上,EF∥AD,EF交AB于点G.
求证:∠AGF=∠F.
请你根据已知条件补充推理过程,并在相应括号内注明理由.
证明:∵ (已知),
∴∠BAD=∠CAD( ).
∵EF∥AD(已知),
∴∠ =∠BAD( ),
∠ =∠CAD( ).
∴∠AGF=∠F( ).
25.如图1,AB∥CD,点E,F分别在直线CD,AB上,∠BEC=2∠BEF,过点A作AG⊥BE的延长线交于点G,交CD于点N,AK平分∠BAG,交EF于点H,交BE于点M.
(1)直接写出∠AHE,∠FAH,∠KEH之间的关系: = + ;
(2)若∠BEF=∠BAK,求∠AHE;
(3)如图2,在(2)的条件下,将△KHE绕着点E以每秒5°的速度逆时针旋转,旋转时间为t,当KE边与射线ED重合时停止,则在旋转过程中,当△KHE的其中一边与△ENG的某一边平行时,直接写出此时t的值.
26.已知:如图,直线a∥b,直线c与直线a、b分别相交于C、D两点,直线d与直线a、b分别相交于A、B两点,点P在直线AB上运动(不与A、B两点重合).
(1)如图1,当点P在线段AB上运动时,总有:∠CPD=∠PCA+∠PDB,请说明理由;
(2)如图2,当点P在线段AB的延长线上运动时,∠CPD、∠PCA、∠PDB之间有怎样的数量关系,并说明理由;
(3)如图3,当点P在线段BA的延长线上运动时,∠CPD、∠PCA、∠PDB之间又有怎样的数量关系(只需直接给出结论)?
27.根据图形及题意填空,并在括号里写上理由.
已知:如图,AD∥BC,AD平分∠EAC.
试说明:∠B=∠C
解:∵AD平分∠EAC(已知)
∴∠1=∠2(角平分线的定义)
∵AD∥BC(已知)
∴∠ =∠ ( )
∠ =∠ ( )
∴∠B=∠C.
参考答案
1.解:∵四边形ABCD是长方形,
∴AD∥BC,
∴∠FEH=∠BFE,∠EHG=∠CGH,
∴∠BFE+∠CGH=∠FEH+∠EHG=118°,
由折叠可知:
EF,GH分别是∠BFP和∠CGP的角平分线,
∴∠PFE=∠BFE,∠PGH=∠CGH,
∴∠PFE+∠PGH=∠BFE+∠CGH=118°,
∴∠BFP+∠CGP=2(∠BFE+∠CGH)=236°,
∴∠PFG+∠PGF=360°﹣(∠BFP+∠CGP)=360°﹣236°=124°,
∴∠FPG=180°﹣(∠PFG+∠PGF)=180°﹣124°=56°.
故选:C.
2.解:如图,标出字母,
∵AB∥CD,
∴∠1+∠FBC+∠2=180°,
∵纸条是对折,
∴∠FBC=∠2,
∴2∠2+∠1=180°,
∵∠1=α,
∴∠2=×(180°﹣α),
∴∠2=90°﹣α,
故选:C.
3.解:∵∠BAC=70°,AF平分∠BAC,
∴∠FAC=∠BAC=35°,
∵DF∥AC,
∴∠1=∠FAC=35°,
故选:B.
4.解:∵AB∥EF,
∴∠BDE=∠E=45°,
又∵∠A=30°,
∴∠B=60°,
∴∠1=∠BDE+∠B=45°+60°=105°,
故选:C.
5.解:如图所示:
∵b∥c,
∴∠1=∠2,
又∵a⊥b,
∴∠1=90°,
∴∠1=∠2=90°,
即a⊥c.
故选:B.
解:过点E作EF∥11,
∵11∥12,EF∥11,
∴EF∥11∥12,
∴∠1=∠AEF=30°,∠FEC+∠3=180°,
∴∠2+∠3=∠AEF+∠FEC+∠3=30°+180°=210°,
故选:C.
7.解:过C作CF∥AB,
∵AB∥DE,
∴AB∥DE∥CF,
∴∠1=∠β,∠α=180°﹣∠2,
∴∠α﹣∠β=180°﹣∠2﹣∠1=180°﹣∠BCD=90°,
故选:D.
8.解:∵AC∥BE,
∴∠A=∠ABE=70°,
故选:A.
9.解:A、两直线平行,同旁内角才互补,故本选项错误;
B、相等的角位置关系不固定,对顶角是其中一种,故本选项错误;
C、距离是一段长度,用具体数值表示,从直线外一点到这条直线的垂线段的长度,叫做这点到这条直线的距离,故本选项错误;
D、经过直线外一点,有且只有一条直线与已知直线平行,故本选项正确.
故选:D.
10.解:A、中的两个角不是由两平行线AB和CD形成的内错角,故无法判断两角的数量关系,故错误;
B、∵AB∥DC,∠1和∠2互为内错角,∴∠1=∠2,故正确.
C、∵AB∥CD,∴∠C+∠ABC=180°;∵直线AD与BC的位置关系不确定,∴∠A与∠ABC的数量关系无法确定,∴∠A与∠C的关系无法确定,故错误;
D、由题意知,直线AD与BC的位置关系不确定,故错误.
故选:B.
11.解:∵直尺的两边互相平行,∠1=35°,
∴∠3=∠1=35°,
∴∠2=35°+30°=65°.
故选:A.
12.解:∵m∥n,∠1=105°,
∴∠2=180°﹣∠1=180°﹣105°=75°.
故选:A.
13.解:∵CE平分∠BCD,∠DCE=18°,
∴∠BCD=2∠DCE=2×18°=36°,
∵AB∥CD,
∴∠B=∠BCD=36°.
故选:B.
14.解:A、∵AB∥CD,
∴∠1+∠2=180°,
故A错误;
B、∵AB∥CD,
∴∠1=∠3,
∵∠2=∠3,
∴∠1=∠2,
故B正确;
C、∵AB∥CD,
∴∠BAD=∠CDA,
若AC∥BD,可得∠1=∠2;
故C错误;
D、若梯形ABCD是等腰梯形,可得∠1=∠2,
故D错误.
故选:B.
15.解:∵∠3是△ADG的外角,
∴∠3=∠A+∠1=30°+25°=55°,
∵l1∥l2,
∴∠3=∠4=55°,
∵∠4+∠EFC=90°,
∴∠EFC=90°﹣55°=35°,
∴∠2=35°.
故选:B.
16.解:∵∠1=80°,a∥b,
∴∠3=∠1=80°,
∴∠2=∠3=80°.
故选:C.
17.解:∵DE⊥CE,
∴∠CED=90°,
∵∠AEC+∠CED+∠DEB=180°,∠DEB=32°,
∴∠AEC=180°﹣∠CED﹣∠DEB=180°﹣90°﹣32°=58°,
∵CD∥AB,
∴∠DCE=∠AEC=58°,
∵CE是∠ACD的平分线,
∴∠ACD=2∠ACE=2×58°=116°,
∴∠ACE=∠AEC,
∵CD∥AB,
∴∠A+∠ACD=180°,
∴∠A=180°﹣∠ACD=180°﹣116°=64°.
故答案为:64°.
18.解:∵AB∥CD,
∴∠CFE=∠AEF,
又∵∠DFE=∠D′FE,∠CFE=2∠CFD′,
∴∠DFE=∠D′FE=3∠CFD′,
∴∠DFE+∠CFE=3∠CFD′+2∠CFD′=180°,
∴∠CFD′=36°,
∴∠AEF=∠CFE=2∠CFD′=72°.
故答案为:72°.
19.解:如图,∵AB∥CD,
∴∠1=∠BAC=118°,
由折叠可得,∠BAD=∠BAC=59°,
∵AB∥CD,
∴∠2=∠BAD=59°,
故答案为:59°.
20.解:∵AD∥BC,
∴∠2=∠DEG,∠EFG=∠DEF=49°,
∵长方形纸片ABCD沿EF折叠后ED与BC的交点为G,
∴∠DEF=∠GEF=49°,
∴∠2=2×49°=98°,
∴∠1=180°﹣98°=82°,
∴∠2﹣∠1=98°﹣82°=16°.
故答案为16°.
21.解:如图,
∵BE⊥EF,
∴∠E=90°,
∵∠B=25°,
∴∠1=65°,
∵AB∥CD,
∴∠EFD=∠1=65°.
故答案为:65°.
22.解:∵AE∥DB,
∴∠1=∠3=3∠2,
∵∠2+∠C=∠3,
∴∠2+∠C=3∠2,
∴∠C=2∠2,
∵∠2=28°.
∴∠C=56°,
故答案为:56°.
23.解:如图,过点F作EF∥AB,
∴∠1+∠3=180°.
∵∠1=100°,
∴∠3=80°.
∵AB∥CD,
∴CD∥EF,
∴∠4+∠2=180°,
∵∠2=120°,
∴∠4=60°.
∴∠α=180°﹣∠3﹣∠4=40°.
故应填40.
24.证明:∵AD是△ABC的角平分线(已知),
∴∠BAD=∠CAD(角平分线的定义),
∵EF∥AD(已知),
∴∠FGA=∠BAD(两直线平行,内错角相等),
∠F=∠CAD(两直线平行,同位角相等),
∴∠AGF=∠F(等量代换),
故答案为:AD是△ABC的角平分线;角平分线的定义;FGA,两直线平行,内错角相等;F,两直线平行,同位角相等;等量代换.
25.解:(1)∵AB∥CD
∴∠KEH=∠AFH
∵∠AHE=∠AFH+∠FAH
∴∠AHE=∠KEH+∠FAH
故答案为:∠AHE;∠KEH;∠FAH;
(2)设∠BEF=x
∵∠BEF=∠BAK,∠BEC=2∠BEF
∴∠BAK=∠BEC=2x
∵AK平分∠BAG
∴∠BAK=∠KAG=2x
由(1)的结论可得:∠AME=2x+2x=4x,∠AHE=2x+3x=5x
∵AG⊥BE
∴∠G=90°
∴∠AME+∠KAG=2x+4x=90°
∴x=15°
∴∠AHE=5x=75°;
(3)由(2)可得,∠KHE=105°,∠BEF=15°,∠HEK=45°,∠NEG=30°,∠ENG=60°
①当KH∥NG时
5°×t=60°﹣30°=30°
∴t=6
②当KE∥GN时
5°×t=60°
∴t=12
③当HE∥GN时
5°×t=45°+60°=105°
∴t=21
④当HK∥EG时,
5°×t=180°﹣30°﹣30°=120°
∴t=24
⑤当HK∥EN时,5t=150°
∴t=30
综上所述,t的值为:6或12或21或24或30.
26.解:(1)证明:如图1,过点P作PE∥a,则∠1=∠CPE.
∵a∥b,PE∥a,
∴PE∥b,
∴∠2=∠DPE,
∴∠3=∠1+∠2,
即∠CPD=∠PCA+∠PDB;
(2)∠CPD=∠PCA﹣∠PDB.
理由:如图2,过点P作PE∥b,则∠2=∠EPD,
∵直线a∥b,
∴a∥PE,
∴∠1=∠EPC,
∵∠3=∠EPC﹣∠EPD,
∴∠3=∠1﹣∠2,
即∠CPD=∠PCA﹣∠PDB;
(3)∠CPD=∠PDB﹣∠PCA.
证明:如图3,设直线AC与DP交于点F,
∵∠PFA是△PCF的外角,
∴∠PFA=∠1+∠3,
∵a∥b,
∴∠2=∠PFA,
∴∠2=∠1+∠3,
∴∠3=∠2﹣∠1,
即∠CPD=∠PDB﹣∠PCA.
27.解:∵AD平分∠EAC,(已知)
∴∠1=∠2,(角平分线的定义)
∵AD∥BC,(已知)
∴∠1=∠B,(两直线平行,同位角相等)
∠2=∠C,(两直线平行,内错角相等)
∴∠B=∠C.
故答案为:1;B;两直线平行,同位角相等;2;C;两直线平行,内错角相等.
