11.4分式的加减法 课件2(北京课改版八年级上)
文档属性
| 名称 | 11.4分式的加减法 课件2(北京课改版八年级上) |

|
|
| 格式 | rar | ||
| 文件大小 | 397.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-21 00:00:00 | ||
图片预览


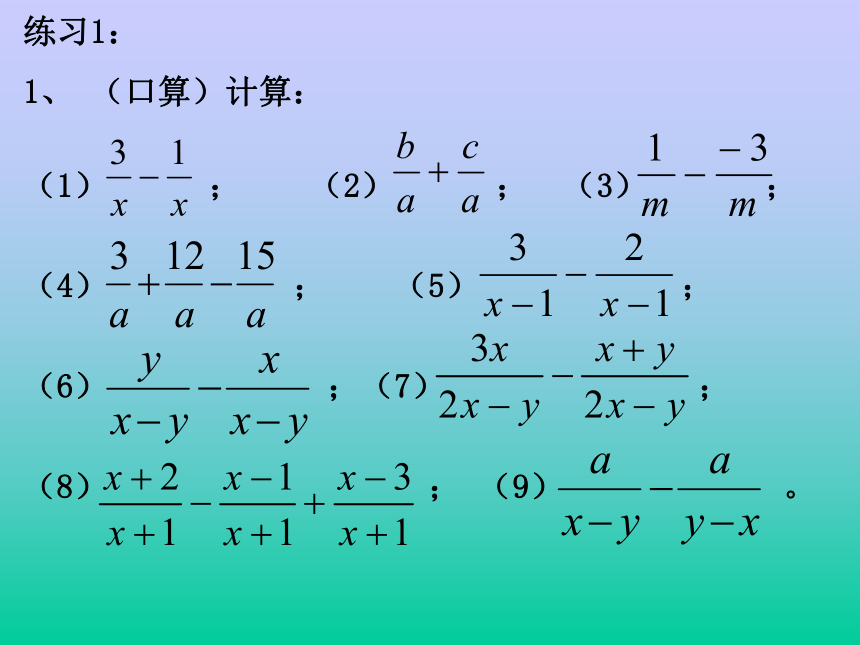
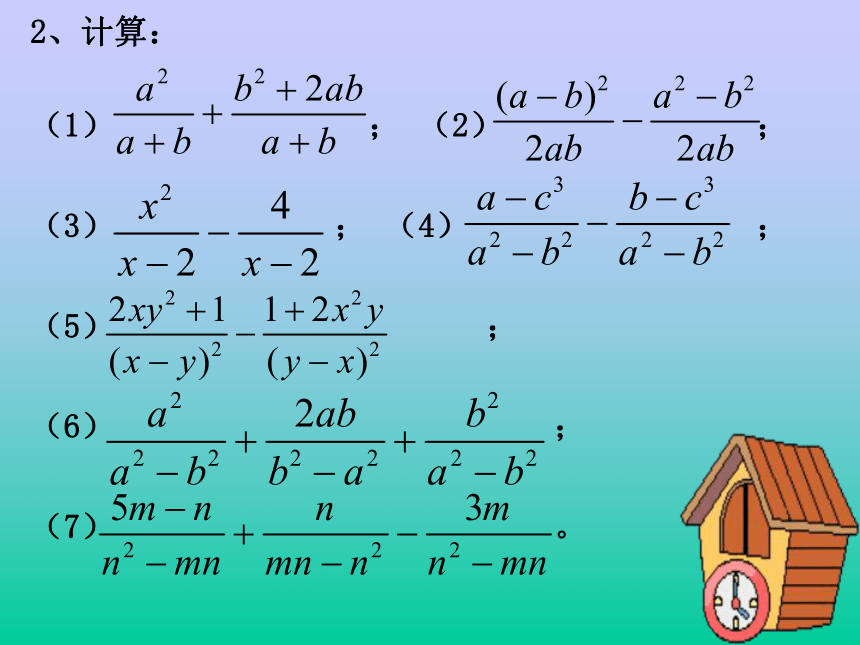




文档简介
课件23张PPT。课题:11.4分式的运算
教学目标:
会进行同分母、异分母的分式加减法,进一步体会通分、约分在分式中的运用。
教材分析:
重点:异分母的分式加减法
难点:对异分母的分式加减法中的通分的理解
教具:多媒体
教学方法:探究、讨论、交流式教学
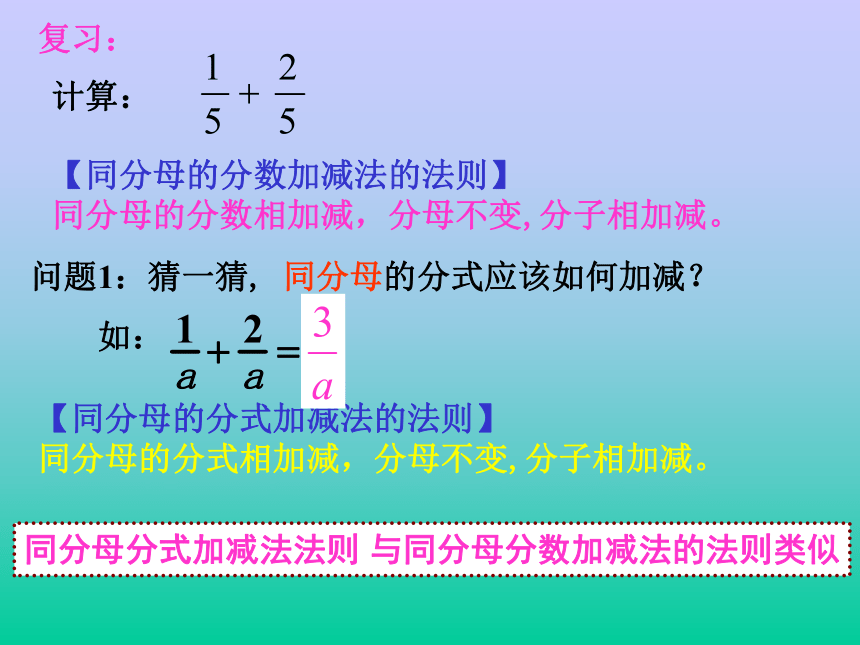
教学过程:11.4分式的加减复习:计算:【同分母的分数加减法的法则】
同分母的分数相加减,分母不变,分子相加减。问题1:猜一猜, 同分母的分式应该如何加减?
如:同分母分式加减法法则 与同分母分数加减法的法则类似【同分母的分式加减法的法则】
同分母的分式相加减,分母不变,分子相加减。练习1:
1、 (口算)计算:
(1) ; (2) ; (3) ;
(4) ; (5) ;
(6) ;(7) ;
(8) ; (9) 。2、计算:
(1) ; (2) ;
(3) ; (4) ;
(5) ;
(6) ;
(7) 。归纳总结1:同分母分式加减的基本步骤:
1、分母不变,把分子相加减。
(1)如果分式的分子是多项式,一定要加上括号;
(2)如果是分子式单项式,可以不加括号。
2、分子相加减时,应先去括号,再合并同类项;
3、最后的结果,应化为最简分式或者整式。问题2:想一想,异分母的分数如何加减?【异分母分数加减法的法则】
通分,把异分母分数化为同分母分数。如 应该怎样计算?问题3:想一想,异分母的分式如何进行加减?如 应该怎样计算?异分母的分式同分母的分式转化通分异分母分式通分时,通常取最简单的公分母(简称最简公分母)作为它们的共同分母。练习2:
1、求下列各组分式的最简公分母:小结1:分式通分时如何确定最简公分母?
(1)系数取各系数的最小公倍数;
(2)凡出现的字母(或含字母的因式)都要取;
(3)相同字母的次数取最高次幂;
(4)当分母是多项式时应先分解因式;
(5)分母前的负号应提到分数线前。
2、计算:3、计算:4、计算: ,并求当a=-3时原式的值。5、阅读下面题目的计算过程。
①
= ②
= ③
= ④
(1)上述计算过程,从哪一步开始错误,请写上该步的代号;
(2)错误原因;
(3)本题的正确结论为: 。 6、请用两种不同的方法进行计算:7、计算:小结2:1、对于混合运算,一般应按运算顺序,有括号先做括号中的运算,若利用乘法对加法的分配律,有时可简化运算,而合理简捷的运算途径是我们始终提倡和追求的。
2、对每一步变形,均应为后边运算打好基础,并为后边运算的简捷合理提供条件.可以说,这是运算能力的一种体现.
3、注意约分时的符号问题。应用:
1、黑猫警长接到举报,A地有坏蛋在搞破坏活动,经分析有两条路都可从警察局到A地,每一条路都是3km,其中第一条是平路,第二条有1km的上坡路和2km的下坡路。黑猫警长在上坡路上的车速是vkm/h,在平路上车速为2vkm/h,在下坡路上的车速为3vkm/h。(1)黑猫警长走第一条平路需要多长时间?你的依据是什么?
(2)那么走第二条路所需的时间呢?
(3)黑猫警长走哪条路花费的时间少?少用多少时间呢?2、台风中心距A市s千米,正以b千米/时的速度向A市移动,救援车队从B市出发,以4倍于台风中心移动的速度向A市前进,已知A、B两地的路程为3s千米,问救援车队能否在台风中心到来前赶到A城?
3、根据规划设计,某市工程队准备在开发区修建一条长1120m的盲道.由于采用新的施工方式,实际每天修建盲道的长度比原计划增加10m,从而缩短了工期.假设原计划每天修建盲道xm,那么
(1)原计划修建这条盲道需要多少天?实际修建这条盲道用了多少天?
(2)实际修建这条盲道的工期比原计划缩短了几天?4、节日期间,几名学生包租了一辆车准备从市区到郊外游览,租金为300元。出发时,又增加了2名同学,总人数达到x名。开始包车的几名学生平均每人可比原来少分摊多少钱?
5、一项工程 , 甲单独做 a 小时完成, 乙单独做 b 小时完成 。甲、乙两人一起完成这项工程,需要多长时间?延伸与拓展链接一:甲、乙两地相距s千米,汽车从甲地到乙地按v千米/时的速度行驶,若按(v+a)千米/时的速度行驶,可提前多少小时到达?链接二:若 ,则 的值等于( )小结:谈谈本节课的收获?小测:
1、填空:
= ; = ;
(3) 的最简公分母是 。
2、计算 的结果是( )
A、 B、 C、 D、 3、计算:板书设计:
课题:
1、同分母的分式加减法法则 投影幕
2、异分母的分式加减法法则
学生板演跟进练习
教学目标:
会进行同分母、异分母的分式加减法,进一步体会通分、约分在分式中的运用。
教材分析:
重点:异分母的分式加减法
难点:对异分母的分式加减法中的通分的理解
教具:多媒体
教学方法:探究、讨论、交流式教学
教学过程:11.4分式的加减复习:计算:【同分母的分数加减法的法则】
同分母的分数相加减,分母不变,分子相加减。问题1:猜一猜, 同分母的分式应该如何加减?
如:同分母分式加减法法则 与同分母分数加减法的法则类似【同分母的分式加减法的法则】
同分母的分式相加减,分母不变,分子相加减。练习1:
1、 (口算)计算:
(1) ; (2) ; (3) ;
(4) ; (5) ;
(6) ;(7) ;
(8) ; (9) 。2、计算:
(1) ; (2) ;
(3) ; (4) ;
(5) ;
(6) ;
(7) 。归纳总结1:同分母分式加减的基本步骤:
1、分母不变,把分子相加减。
(1)如果分式的分子是多项式,一定要加上括号;
(2)如果是分子式单项式,可以不加括号。
2、分子相加减时,应先去括号,再合并同类项;
3、最后的结果,应化为最简分式或者整式。问题2:想一想,异分母的分数如何加减?【异分母分数加减法的法则】
通分,把异分母分数化为同分母分数。如 应该怎样计算?问题3:想一想,异分母的分式如何进行加减?如 应该怎样计算?异分母的分式同分母的分式转化通分异分母分式通分时,通常取最简单的公分母(简称最简公分母)作为它们的共同分母。练习2:
1、求下列各组分式的最简公分母:小结1:分式通分时如何确定最简公分母?
(1)系数取各系数的最小公倍数;
(2)凡出现的字母(或含字母的因式)都要取;
(3)相同字母的次数取最高次幂;
(4)当分母是多项式时应先分解因式;
(5)分母前的负号应提到分数线前。
2、计算:3、计算:4、计算: ,并求当a=-3时原式的值。5、阅读下面题目的计算过程。
①
= ②
= ③
= ④
(1)上述计算过程,从哪一步开始错误,请写上该步的代号;
(2)错误原因;
(3)本题的正确结论为: 。 6、请用两种不同的方法进行计算:7、计算:小结2:1、对于混合运算,一般应按运算顺序,有括号先做括号中的运算,若利用乘法对加法的分配律,有时可简化运算,而合理简捷的运算途径是我们始终提倡和追求的。
2、对每一步变形,均应为后边运算打好基础,并为后边运算的简捷合理提供条件.可以说,这是运算能力的一种体现.
3、注意约分时的符号问题。应用:
1、黑猫警长接到举报,A地有坏蛋在搞破坏活动,经分析有两条路都可从警察局到A地,每一条路都是3km,其中第一条是平路,第二条有1km的上坡路和2km的下坡路。黑猫警长在上坡路上的车速是vkm/h,在平路上车速为2vkm/h,在下坡路上的车速为3vkm/h。(1)黑猫警长走第一条平路需要多长时间?你的依据是什么?
(2)那么走第二条路所需的时间呢?
(3)黑猫警长走哪条路花费的时间少?少用多少时间呢?2、台风中心距A市s千米,正以b千米/时的速度向A市移动,救援车队从B市出发,以4倍于台风中心移动的速度向A市前进,已知A、B两地的路程为3s千米,问救援车队能否在台风中心到来前赶到A城?
3、根据规划设计,某市工程队准备在开发区修建一条长1120m的盲道.由于采用新的施工方式,实际每天修建盲道的长度比原计划增加10m,从而缩短了工期.假设原计划每天修建盲道xm,那么
(1)原计划修建这条盲道需要多少天?实际修建这条盲道用了多少天?
(2)实际修建这条盲道的工期比原计划缩短了几天?4、节日期间,几名学生包租了一辆车准备从市区到郊外游览,租金为300元。出发时,又增加了2名同学,总人数达到x名。开始包车的几名学生平均每人可比原来少分摊多少钱?
5、一项工程 , 甲单独做 a 小时完成, 乙单独做 b 小时完成 。甲、乙两人一起完成这项工程,需要多长时间?延伸与拓展链接一:甲、乙两地相距s千米,汽车从甲地到乙地按v千米/时的速度行驶,若按(v+a)千米/时的速度行驶,可提前多少小时到达?链接二:若 ,则 的值等于( )小结:谈谈本节课的收获?小测:
1、填空:
= ; = ;
(3) 的最简公分母是 。
2、计算 的结果是( )
A、 B、 C、 D、 3、计算:板书设计:
课题:
1、同分母的分式加减法法则 投影幕
2、异分母的分式加减法法则
学生板演跟进练习
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
