2025人教B版高中数学必修第二册同步练习题--专题强化练3 统计思想的应用(含解析)
文档属性
| 名称 | 2025人教B版高中数学必修第二册同步练习题--专题强化练3 统计思想的应用(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 554.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-19 19:44:48 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025人教B版高中数学必修第二册
专题强化练3 统计思想的应用
1.甲、乙两台机床同时生产一种零件,10天中两台机床每天生产出的次品数如下:
甲:0,1,0,2,2,0,3,1,2,4;
乙:2,2,1,1,1,2,1,1,0,1;
若分别表示甲、乙两台机床次品数的平均数,分别表示甲、乙两台机床次品数的方差,则下列选项正确的是( )
A.
C.
2.(2024四川成都开学考试)某保险公司为客户定制了A,B,C,D,E共5个险种,并对5个险种参保客户进行抽样调查,得出如下的统计图:
参保人数比例
不同年龄段的参保人群人均参保费用
参保险种比例
用样本估计总体,下列说法错误的是( )
A.57周岁及以上参保人数最少
B.18~30周岁参保人群的参保总费用最少
C.C险种更受参保人青睐
D.31周岁及以上参保人群约占参保人群的80%
3.甲、乙两人在5天中每天加工的零件个数用茎叶图表示如图,中间的一列数字表示零件个数的十位数,两边的数字表示零件个数的个位数,下列结论正确的是( )
A.在这5天中,甲、乙两人加工的零件个数的极差相同
B.在这5天中,甲、乙两人加工的零件个数的中位数相同
C.在这5天中,甲日均加工的零件个数大于乙日均加工的零件个数
D.在这5天中,甲加工的零件个数的方差小于乙加工的零件个数的方差
4.(2024四川凉山期末)下图展示了2007年至2022年中国和美国从对方国家进口的总额占本国总进口额的比重变化情况,从图中得出如下结论最准确的是( )
A.在2007年到2022年期间,中国对美国的出口总额占比相对较高,中国对美国的出口总额占美国全部进口总额的比例一直保持在15%以上
B.在2007年到2022年期间,中国从美国的进口总额占中国总进口额的比重出现了大幅波动,在2015年时,这一比例达到峰值,但在2019年和2021年时下降至最低点
C.美国从中国进口的总额占比逐年下降,2018年后美国从中国进口的总额占比下降速度加快
D.中国市场对美国的依赖度正在降低,从长期趋势来看,中国从美国的进口总额所占比例在2015年达到峰值后开始逐渐下降
5.为了解某校高三学生的视力情况,随机抽查了该校100名高三学生的视力,得到频率分布直方图如图所示.由于不慎将部分数据丢失,但知道前4组的频数分别为x1,x2,x3,x4,且满足,后6组的频数分别为y1,y2,y3,y4,y5,y6,且后6组相邻频数之间差值相同,设最大频率为a,视力在4.6到5.0之间的学生人数为b,则a,b的值分别为( )
A.0.27,78 B.0.27,83
C.2.7,78 D.2.7,83
6.某工厂的甲、乙、丙3条生产线共生产了16 800件某种产品,为检查这批产品的质量,决定采用分层抽样的方法进行抽样.已知从甲、乙、丙3条生产线抽取的产品件数分别是a,b,c,且2b=a+c,则乙生产线生产了 件产品.
7.已知6个正整数,它们的平均数是5,中位数是4,唯一的众数是3,则这6个数的极差最大时,方差的值是 .
8.一所初级中学为了估计全体学生的平均身高和方差,通过抽样的方法从初一年级随机抽取了30人,计算得这30人的平均身高为154 cm,方差为30;从初二年级随机抽取了40人,计算得这40人的平均身高为167 cm,方差为20;从初三年级随机抽取了30人,计算得这30人的平均身高为170 cm,方差为10.依据以上数据,若用样本的方差估计全校学生身高的方差,则全校学生身高方差的估计值为 .
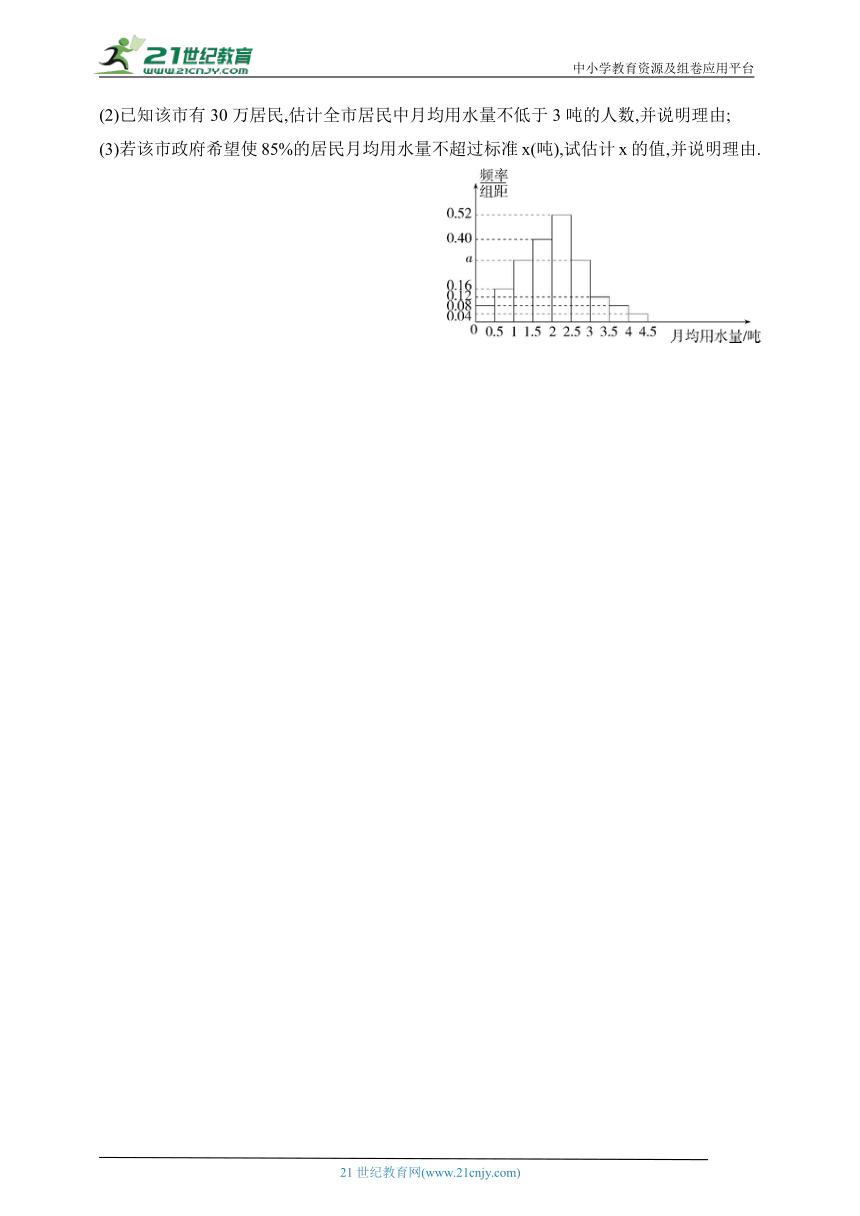
9.某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解全市居民用水量的分布情况,通过随机抽样获得了100位居民某年的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[3.5,4),[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(1)求a的值,并估计该市居民月均用水量的众数、平均数(同一组中的数据用该组区间的中点值作代表);
(2)已知该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(3)若该市政府希望使85%的居民月均用水量不超过标准x(吨),试估计x的值,并说明理由.
答案与分层梯度式解析
专题强化练3 统计思想的应用
1.B 2.B 3.C 4.D 5.A
1.B 依题意得×(2+2+1+1+1+2+1+1+0+1)=1.2,
×[(-1.5)2+(-0.5)2+(-1.5)2+0.52+0.52+(-1.5)2+1.52+(-0.5)2+0.52+2.52]=1.65,
×[0.82+0.82+(-0.2)2+(-0.2)2+(-0.2)2+0.82+(-0.2)2+(-0.2)2+(-1.2)2+(-0.2)2]=0.36.
因此,故选B.
2.B 57周岁及以上参保人数所占比例是10%,是最少的,A中说法正确.
18~30周岁参保人群人均参保费用比57周岁及以上参保人群人均参保费用的一半还多,而18~30周岁参保人数比例是57周岁及以上参保人数比例的两倍,所以57周岁及以上参保人群的参保总费用最少,B中说法错误.
C险种参保比例为0.358,是最多的,所以C中说法正确.
31周岁及以上参保人群约占参保人群的30%+40%+10%=80%,D中说法正确.
3.C 由题图知,甲这5天中每天加工的零件个数分别为18,19,23,27,28;乙这5天中每天加工的零件个数分别为17,19,21,23,25.
对于A,甲加工的零件个数的极差为28-18=10,乙加工的零件个数的极差为25-17=8,故A错误;
对于B,甲加工的零件个数的中位数为23,乙加工的零件个数的中位数为21,故B错误;
对于C,甲加工的零件个数的平均数为=23,乙加工的零件个数的平均数为=21,故C正确;
对于D,甲加工的零件个数的方差为=16.4,乙加工的零件个数的方差为=8,故D错误.故选C.
4.D 在2007年到2022年期间,中国对美国的出口总额占比相对较高,中国对美国的出口总额占美国全部进口总额的比例,2008年为15%,2022年为14.2%,故A错误;
在2007年到2022年期间,中国从美国的进口总额占中国总进口额的比重出现了大幅波动,在2015年时,这一比重达到峰值10.05%,但2022年时下降至最低点6.5%,故B错误;
美国从中国进口的总额占比,2019年为16.3%,2020年为16.5%,故C错误;
由题图得D正确.
5.A 由题意得视力在4.5到4.6之间的频率为0.09,在4.6到4.7之间的频率为0.27,即a=0.27.由题可设后6组相邻频数之间的差值为100d(d<0),则后6组的频率依次为0.27,0.27+d,0.27+2d,0.27+3d,0.27+4d,0.27+5d,∴6×0.27+15d=1-0.01-0.03-0.09,∴d=-0.05.∴b=(0.27×4+6d)×100=78.
6.答案 5 600
解析 设甲、乙、丙3条生产线各生产了T甲,T乙,T丙件产品,则a∶b∶c=T甲∶T乙∶T丙,又2b=a+c,
所以所以T乙=5 600.
7.答案
解析 易知当这6个数的极差最大时,最小的正整数为1.
因为唯一的众数是3,所以3至少出现两次.
若这6个数中有3个3,则这6个数的中位数最大为3,与已知矛盾,
故这6个数中只有2个3,且由中位数为4,知这6个数从小到大排列后前4个数为1,3,3,5,设后2个数为x,y,
由平均数为5,可得(1+3+3+5+x+y)×=5,故x+y=18,
若极差最大,则y最大,又x的最小值为6,所以y的最大值为12.
此时6个数的方差为.
8.答案 64.4
解析 初一学生的样本记为x1,x2,…,x30,平均数记为,方差记为,初二学生的样本记为y1,y2,…,y40,平均数记为
9.解析 (1)由题图可得(0.08+0.16+a+0.40+0.52+a+0.12+0.08+0.04)×0.5=1,解得a=0.30.
估计该市居民月均用水量的众数为=2.25(吨),平均数为0.25×0.08×0.5+0.75×0.16×0.5+1.25×0.3×0.5+1.75×0.4×0.5+2.25×0.52×0.5+2.75×0.3×0.5+3.25×0.12×0.5+3.75×0.08×0.5+4.25×0.04×0.5=2.035(吨).
(2)由题图知,100位居民中月均用水量不低于3吨的频率为(0.12+0.08+0.04)×0.5=0.12.由此可以估计该市30万居民中月均用水量不低于3吨的人数为300 000×0.12=36 000.
(3)由题图得前5组的频率之和为(0.08+0.16+0.30+0.40+0.52)×0.5=0.73<0.85,前6组的频率之和为(0.08+0.16+0.30+0.40+0.52+0.30)×0.5=0.88>0.85,所以2.5由0.3×(x-2.5)=0.85-0.73,解得x=2.9.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教B版高中数学必修第二册
专题强化练3 统计思想的应用
1.甲、乙两台机床同时生产一种零件,10天中两台机床每天生产出的次品数如下:
甲:0,1,0,2,2,0,3,1,2,4;
乙:2,2,1,1,1,2,1,1,0,1;
若分别表示甲、乙两台机床次品数的平均数,分别表示甲、乙两台机床次品数的方差,则下列选项正确的是( )
A.
C.
2.(2024四川成都开学考试)某保险公司为客户定制了A,B,C,D,E共5个险种,并对5个险种参保客户进行抽样调查,得出如下的统计图:
参保人数比例
不同年龄段的参保人群人均参保费用
参保险种比例
用样本估计总体,下列说法错误的是( )
A.57周岁及以上参保人数最少
B.18~30周岁参保人群的参保总费用最少
C.C险种更受参保人青睐
D.31周岁及以上参保人群约占参保人群的80%
3.甲、乙两人在5天中每天加工的零件个数用茎叶图表示如图,中间的一列数字表示零件个数的十位数,两边的数字表示零件个数的个位数,下列结论正确的是( )
A.在这5天中,甲、乙两人加工的零件个数的极差相同
B.在这5天中,甲、乙两人加工的零件个数的中位数相同
C.在这5天中,甲日均加工的零件个数大于乙日均加工的零件个数
D.在这5天中,甲加工的零件个数的方差小于乙加工的零件个数的方差
4.(2024四川凉山期末)下图展示了2007年至2022年中国和美国从对方国家进口的总额占本国总进口额的比重变化情况,从图中得出如下结论最准确的是( )
A.在2007年到2022年期间,中国对美国的出口总额占比相对较高,中国对美国的出口总额占美国全部进口总额的比例一直保持在15%以上
B.在2007年到2022年期间,中国从美国的进口总额占中国总进口额的比重出现了大幅波动,在2015年时,这一比例达到峰值,但在2019年和2021年时下降至最低点
C.美国从中国进口的总额占比逐年下降,2018年后美国从中国进口的总额占比下降速度加快
D.中国市场对美国的依赖度正在降低,从长期趋势来看,中国从美国的进口总额所占比例在2015年达到峰值后开始逐渐下降
5.为了解某校高三学生的视力情况,随机抽查了该校100名高三学生的视力,得到频率分布直方图如图所示.由于不慎将部分数据丢失,但知道前4组的频数分别为x1,x2,x3,x4,且满足,后6组的频数分别为y1,y2,y3,y4,y5,y6,且后6组相邻频数之间差值相同,设最大频率为a,视力在4.6到5.0之间的学生人数为b,则a,b的值分别为( )
A.0.27,78 B.0.27,83
C.2.7,78 D.2.7,83
6.某工厂的甲、乙、丙3条生产线共生产了16 800件某种产品,为检查这批产品的质量,决定采用分层抽样的方法进行抽样.已知从甲、乙、丙3条生产线抽取的产品件数分别是a,b,c,且2b=a+c,则乙生产线生产了 件产品.
7.已知6个正整数,它们的平均数是5,中位数是4,唯一的众数是3,则这6个数的极差最大时,方差的值是 .
8.一所初级中学为了估计全体学生的平均身高和方差,通过抽样的方法从初一年级随机抽取了30人,计算得这30人的平均身高为154 cm,方差为30;从初二年级随机抽取了40人,计算得这40人的平均身高为167 cm,方差为20;从初三年级随机抽取了30人,计算得这30人的平均身高为170 cm,方差为10.依据以上数据,若用样本的方差估计全校学生身高的方差,则全校学生身高方差的估计值为 .
9.某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解全市居民用水量的分布情况,通过随机抽样获得了100位居民某年的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[3.5,4),[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(1)求a的值,并估计该市居民月均用水量的众数、平均数(同一组中的数据用该组区间的中点值作代表);
(2)已知该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(3)若该市政府希望使85%的居民月均用水量不超过标准x(吨),试估计x的值,并说明理由.
答案与分层梯度式解析
专题强化练3 统计思想的应用
1.B 2.B 3.C 4.D 5.A
1.B 依题意得×(2+2+1+1+1+2+1+1+0+1)=1.2,
×[(-1.5)2+(-0.5)2+(-1.5)2+0.52+0.52+(-1.5)2+1.52+(-0.5)2+0.52+2.52]=1.65,
×[0.82+0.82+(-0.2)2+(-0.2)2+(-0.2)2+0.82+(-0.2)2+(-0.2)2+(-1.2)2+(-0.2)2]=0.36.
因此,故选B.
2.B 57周岁及以上参保人数所占比例是10%,是最少的,A中说法正确.
18~30周岁参保人群人均参保费用比57周岁及以上参保人群人均参保费用的一半还多,而18~30周岁参保人数比例是57周岁及以上参保人数比例的两倍,所以57周岁及以上参保人群的参保总费用最少,B中说法错误.
C险种参保比例为0.358,是最多的,所以C中说法正确.
31周岁及以上参保人群约占参保人群的30%+40%+10%=80%,D中说法正确.
3.C 由题图知,甲这5天中每天加工的零件个数分别为18,19,23,27,28;乙这5天中每天加工的零件个数分别为17,19,21,23,25.
对于A,甲加工的零件个数的极差为28-18=10,乙加工的零件个数的极差为25-17=8,故A错误;
对于B,甲加工的零件个数的中位数为23,乙加工的零件个数的中位数为21,故B错误;
对于C,甲加工的零件个数的平均数为=23,乙加工的零件个数的平均数为=21,故C正确;
对于D,甲加工的零件个数的方差为=16.4,乙加工的零件个数的方差为=8,故D错误.故选C.
4.D 在2007年到2022年期间,中国对美国的出口总额占比相对较高,中国对美国的出口总额占美国全部进口总额的比例,2008年为15%,2022年为14.2%,故A错误;
在2007年到2022年期间,中国从美国的进口总额占中国总进口额的比重出现了大幅波动,在2015年时,这一比重达到峰值10.05%,但2022年时下降至最低点6.5%,故B错误;
美国从中国进口的总额占比,2019年为16.3%,2020年为16.5%,故C错误;
由题图得D正确.
5.A 由题意得视力在4.5到4.6之间的频率为0.09,在4.6到4.7之间的频率为0.27,即a=0.27.由题可设后6组相邻频数之间的差值为100d(d<0),则后6组的频率依次为0.27,0.27+d,0.27+2d,0.27+3d,0.27+4d,0.27+5d,∴6×0.27+15d=1-0.01-0.03-0.09,∴d=-0.05.∴b=(0.27×4+6d)×100=78.
6.答案 5 600
解析 设甲、乙、丙3条生产线各生产了T甲,T乙,T丙件产品,则a∶b∶c=T甲∶T乙∶T丙,又2b=a+c,
所以所以T乙=5 600.
7.答案
解析 易知当这6个数的极差最大时,最小的正整数为1.
因为唯一的众数是3,所以3至少出现两次.
若这6个数中有3个3,则这6个数的中位数最大为3,与已知矛盾,
故这6个数中只有2个3,且由中位数为4,知这6个数从小到大排列后前4个数为1,3,3,5,设后2个数为x,y,
由平均数为5,可得(1+3+3+5+x+y)×=5,故x+y=18,
若极差最大,则y最大,又x的最小值为6,所以y的最大值为12.
此时6个数的方差为.
8.答案 64.4
解析 初一学生的样本记为x1,x2,…,x30,平均数记为,方差记为,初二学生的样本记为y1,y2,…,y40,平均数记为
9.解析 (1)由题图可得(0.08+0.16+a+0.40+0.52+a+0.12+0.08+0.04)×0.5=1,解得a=0.30.
估计该市居民月均用水量的众数为=2.25(吨),平均数为0.25×0.08×0.5+0.75×0.16×0.5+1.25×0.3×0.5+1.75×0.4×0.5+2.25×0.52×0.5+2.75×0.3×0.5+3.25×0.12×0.5+3.75×0.08×0.5+4.25×0.04×0.5=2.035(吨).
(2)由题图知,100位居民中月均用水量不低于3吨的频率为(0.12+0.08+0.04)×0.5=0.12.由此可以估计该市30万居民中月均用水量不低于3吨的人数为300 000×0.12=36 000.
(3)由题图得前5组的频率之和为(0.08+0.16+0.30+0.40+0.52)×0.5=0.73<0.85,前6组的频率之和为(0.08+0.16+0.30+0.40+0.52+0.30)×0.5=0.88>0.85,所以2.5
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
