2025人教B版高中数学必修第二册同步练习题--4.1.1 实数指数幂及其运算(含解析)
文档属性
| 名称 | 2025人教B版高中数学必修第二册同步练习题--4.1.1 实数指数幂及其运算(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 307.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-19 00:00:00 | ||
图片预览



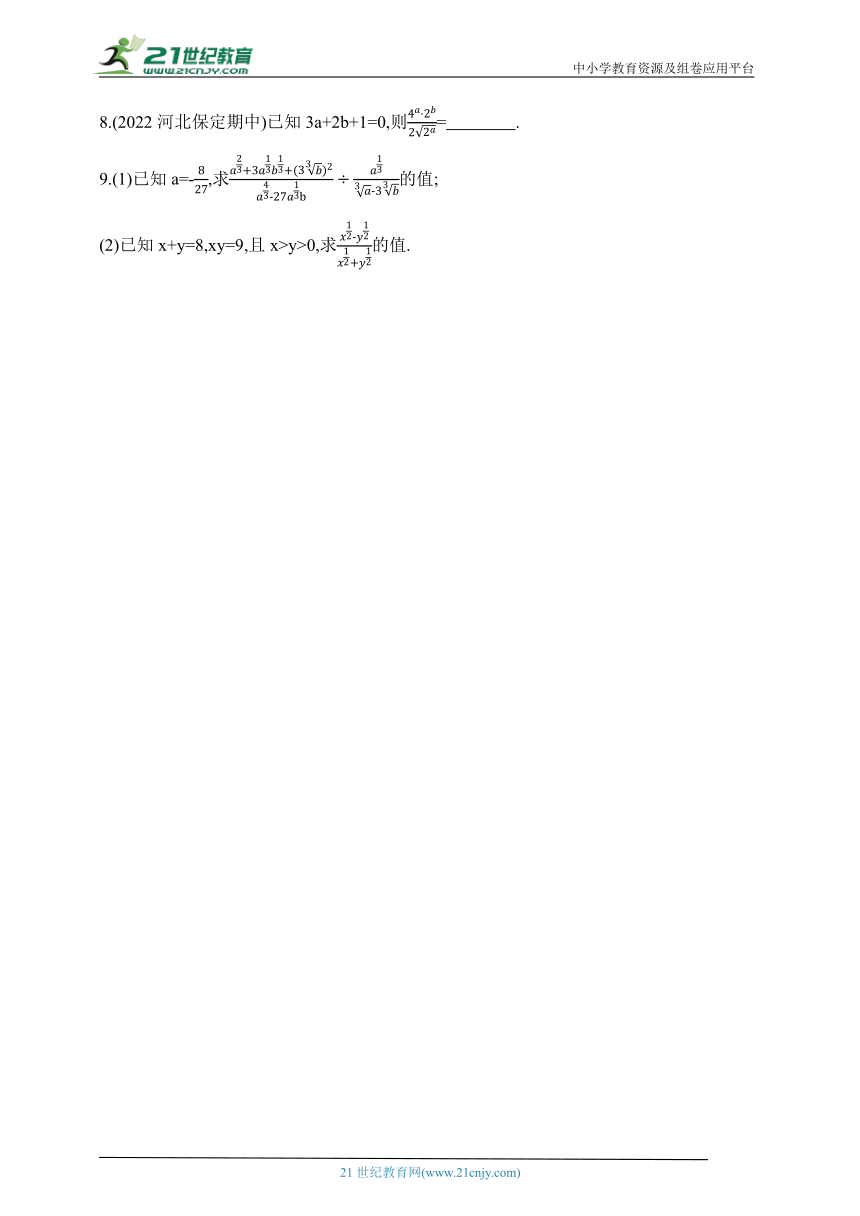
文档简介
中小学教育资源及组卷应用平台
2025人教B版高中数学必修第二册
第四章 指数函数、对数函数与幂函数
4.1 指数与指数函数
4.1.1 实数指数幂及其运算
基础过关练
题组一 根式的概念及性质
1.(2024浙江台州黄岩中学期中)已知n∈N+,a∈R,则“=a”是“a>0”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
2.(2023吉林省实验中学期中)化简:=( )
A.0 B.2π-8 C.2π-8或0 D.8-2π
3.若)3,则实数a的取值范围是 .
题组二 根式与分数指数幂的运算
4.(多选题)(2024云南昭通期中)下列各式中,正确的是( )
A.
C.
5.(2022浙江温州新力量联盟期中联考)已知a>0,将表示成分数指数幂,其结果是 ( )
A. C.
6.(2022江苏沭阳如东高级中学月考)已知x<0,y>0,则可化为( )
A.-x2y
C.-3x2y D.3x2y
7.下列等式不可能成立的是( )
A.am+3·a·an-1=am+n·a·a2
B.(a·b)m+3=am+1·(a·b2)2·bm-1
C.[(x-a)3]2[(x+a)3]2=[(a-x)2(x+a)2]3
D.[(m-n)3]5=[(n-m)2]5(n-m)5(m≠n)
8.(2023广东广州华师附中期中)
(1)若m=,求的值;
(2)若a=27,b=16,求的值.
题组三 指数幂的条件求值问题
9.(2024广东汕头金山中学期中)已知x>1,x+x-1=6,则= .
10.设α,β是方程5x2+10x+1=0的两个实数根,则2α·2β= ,(2α)β= .
11.(2024上海财经大学附属北郊高级中学期中)若a2x=3,且a>0,则= .
能力提升练
题组一 根式与分数指数幂的运算
1.若a<,则化简的结果是( )
A.
C.-
2.(多选题)(2022广东茂名期中)下列化简结果一定正确的是(字母均为正数)( )
A.=1
B.=a-4b6
C.ac
D.(-2)=24y
3.A4纸是生活中最常用的一种纸张规格.A系列的纸张规格特色在于:①A0,A1,A2,A3等,所有尺寸的纸张长宽比都相同;②以前一个序号的纸张的两条长边中点连线为折线对折裁剪分开后,可以得到两张后面序号大小的纸,比如1张A0纸对裁后可以得到2张A1纸,1张A1纸对裁后可以得到2张A2纸,依此类推.A系列纸张之所以具备这种特性,是因为它们的长宽比均为∶1.已知A0纸规格为84.1厘米×118.9厘米,118.9÷84.1≈1.41≈,那么A4纸的长度约为( )
A.14.8厘米 B.21.0厘米
C.29.7厘米 D.42.0厘米
4.(2024重庆西南大学附中期中)
(1)计算:(0.008 1×81-0.25+;
(2)化简:(a>0).
题组二 指数幂的条件求值问题
5.若3α=5,3β=6,则=( )
A. D.325α-6β
6.(多选题)(2023福建厦门双十中学期中)已知实数a满足a+a-1=4,则( )
A.a2+a-2=14 B.a-a-1=2
C.
7.已知a>1,=4,则的值为 .
8.(2022河北保定期中)已知3a+2b+1=0,则= .
9.(1)已知a=-,求的值;
(2)已知x+y=8,xy=9,且x>y>0,求的值.
答案与分层梯度式解析
第四章 指数函数、对数函数与幂函数
4.1 指数与指数函数
4.1.1 实数指数幂及其运算
基础过关练
1.B 2.A 4.AC 5.C 6.B 7.D
1.B 当n为奇数时,=a,
当n为偶数时,=a,则a≥0,所以“=a”是“a>0”的必要不充分条件.
2.A 原式=|π-4|+(π-4)=4-π+π-4=0,故选A.
3.答案
解析 由题意得|2a-1|=1-2a,所以2a-1≤0,解得a≤.故实数a的取值范围是.
4.AC =(a·b-1)2=a2b-2;≠(a-b.
故选AC.
5.C .故选C.
方法点拨 当表达式中的根号较多时,要弄清被开方数,由内向外进行转化、运算.
6.B ∵x<0,y>0,∴x2y.故选B.
7.D 对于A,左边=am+3+1+n-1=am+n+3,右边=am+n+1+2=am+n+3,左边=右边,故A中等式成立;对于B,左边=am+3bm+3,右边=am+1·a2·b4·bm-1=am+1+2·b4+m-1=am+3bm+3,左边=右边,故B中等式成立;对于C,左边=(x-a)6(x+a)6=(x2-a2)6,右边=[(x2-a2)2]3=(x2-a2)6,左边=右边,故C中等式成立;对于D,若m-n<0,则左边<0,右边>0,左边≠右边,若m-n>0,则左边>0,右边<0,左边≠右边,故D中等式不可能成立.
8.解析 (1)因为m=,所以.
(2)
=,
因为a=27,b=16,所以原式=4×2=6.
9.答案 2
解析 -2=4,又x>1,所以>0,所以=2.
10.答案
解析 利用一元二次方程根与系数的关系,得α+β=-2,αβ=,则2α·2β=2α+β=2-2=.
11.答案
解析 .
能力提升练
1.B 2.BD 3.C 5.B 6.ACD
1.B ∵a<.故选B.
2.BD =a5;
=a-4b6;
ac-2;
(-2=24y.故选BD.
3.答案 C
信息提取 ①A0,A1,A2,A3等,所有尺寸的纸张长宽比都为∶1;②以前一个序号的纸张的两条长边中点连线为折线对折裁剪分开后,可以得到两张后面序号大小的纸;③A0纸规格为84.1厘米×118.9厘米.
数学建模 由生活中常见纸张规格之间的长度关系建立与指数幂有关的数学模型,根据题意设出A4纸的长度,利用指数幂的运算法则求解.
解析 设A4纸的长度为x 厘米,则A3纸的长度为x 厘米,依此类推可以得到:)4=4,解得x≈29.7,故选C.
4.解析 (1)原式=(0.34-3-1×(34+π-3=π.
(2)原式==a2.
5.B ∵3α=5,3β=6,∴33α=53=125,32β=62=36,
∴=33α-2β.
6.ACD 因为a+a-1=4,所以a>0,a2+a-2=(a+a-1)2-2a·a-1=16-2=14,故A正确;
(a-a-1)2=a2+a-2-2a·a-1=12,所以a-a-1=±2,故B错误;
(=6,因为a>0,所以>0,所以,故C正确;
,故D正确.
7.答案
解析 由=4,即=4,得()2=a+a-1+2=16,所以a+a-1=14,
所以()2=a+a-1-2=12,因为a>1,所以,所以,
所以.
8.答案
解析 .因为3a+2b+1=0,所以,所以.
9.解析 (1)原式=
=.
将a=-代入,得原式=.
(2)由题意得(x-y)2=(x+y)2-4xy=64-36=28,
∵x>y>0,∴x-y=2.
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教B版高中数学必修第二册
第四章 指数函数、对数函数与幂函数
4.1 指数与指数函数
4.1.1 实数指数幂及其运算
基础过关练
题组一 根式的概念及性质
1.(2024浙江台州黄岩中学期中)已知n∈N+,a∈R,则“=a”是“a>0”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
2.(2023吉林省实验中学期中)化简:=( )
A.0 B.2π-8 C.2π-8或0 D.8-2π
3.若)3,则实数a的取值范围是 .
题组二 根式与分数指数幂的运算
4.(多选题)(2024云南昭通期中)下列各式中,正确的是( )
A.
C.
5.(2022浙江温州新力量联盟期中联考)已知a>0,将表示成分数指数幂,其结果是 ( )
A. C.
6.(2022江苏沭阳如东高级中学月考)已知x<0,y>0,则可化为( )
A.-x2y
C.-3x2y D.3x2y
7.下列等式不可能成立的是( )
A.am+3·a·an-1=am+n·a·a2
B.(a·b)m+3=am+1·(a·b2)2·bm-1
C.[(x-a)3]2[(x+a)3]2=[(a-x)2(x+a)2]3
D.[(m-n)3]5=[(n-m)2]5(n-m)5(m≠n)
8.(2023广东广州华师附中期中)
(1)若m=,求的值;
(2)若a=27,b=16,求的值.
题组三 指数幂的条件求值问题
9.(2024广东汕头金山中学期中)已知x>1,x+x-1=6,则= .
10.设α,β是方程5x2+10x+1=0的两个实数根,则2α·2β= ,(2α)β= .
11.(2024上海财经大学附属北郊高级中学期中)若a2x=3,且a>0,则= .
能力提升练
题组一 根式与分数指数幂的运算
1.若a<,则化简的结果是( )
A.
C.-
2.(多选题)(2022广东茂名期中)下列化简结果一定正确的是(字母均为正数)( )
A.=1
B.=a-4b6
C.ac
D.(-2)=24y
3.A4纸是生活中最常用的一种纸张规格.A系列的纸张规格特色在于:①A0,A1,A2,A3等,所有尺寸的纸张长宽比都相同;②以前一个序号的纸张的两条长边中点连线为折线对折裁剪分开后,可以得到两张后面序号大小的纸,比如1张A0纸对裁后可以得到2张A1纸,1张A1纸对裁后可以得到2张A2纸,依此类推.A系列纸张之所以具备这种特性,是因为它们的长宽比均为∶1.已知A0纸规格为84.1厘米×118.9厘米,118.9÷84.1≈1.41≈,那么A4纸的长度约为( )
A.14.8厘米 B.21.0厘米
C.29.7厘米 D.42.0厘米
4.(2024重庆西南大学附中期中)
(1)计算:(0.008 1×81-0.25+;
(2)化简:(a>0).
题组二 指数幂的条件求值问题
5.若3α=5,3β=6,则=( )
A. D.325α-6β
6.(多选题)(2023福建厦门双十中学期中)已知实数a满足a+a-1=4,则( )
A.a2+a-2=14 B.a-a-1=2
C.
7.已知a>1,=4,则的值为 .
8.(2022河北保定期中)已知3a+2b+1=0,则= .
9.(1)已知a=-,求的值;
(2)已知x+y=8,xy=9,且x>y>0,求的值.
答案与分层梯度式解析
第四章 指数函数、对数函数与幂函数
4.1 指数与指数函数
4.1.1 实数指数幂及其运算
基础过关练
1.B 2.A 4.AC 5.C 6.B 7.D
1.B 当n为奇数时,=a,
当n为偶数时,=a,则a≥0,所以“=a”是“a>0”的必要不充分条件.
2.A 原式=|π-4|+(π-4)=4-π+π-4=0,故选A.
3.答案
解析 由题意得|2a-1|=1-2a,所以2a-1≤0,解得a≤.故实数a的取值范围是.
4.AC =(a·b-1)2=a2b-2;≠(a-b.
故选AC.
5.C .故选C.
方法点拨 当表达式中的根号较多时,要弄清被开方数,由内向外进行转化、运算.
6.B ∵x<0,y>0,∴x2y.故选B.
7.D 对于A,左边=am+3+1+n-1=am+n+3,右边=am+n+1+2=am+n+3,左边=右边,故A中等式成立;对于B,左边=am+3bm+3,右边=am+1·a2·b4·bm-1=am+1+2·b4+m-1=am+3bm+3,左边=右边,故B中等式成立;对于C,左边=(x-a)6(x+a)6=(x2-a2)6,右边=[(x2-a2)2]3=(x2-a2)6,左边=右边,故C中等式成立;对于D,若m-n<0,则左边<0,右边>0,左边≠右边,若m-n>0,则左边>0,右边<0,左边≠右边,故D中等式不可能成立.
8.解析 (1)因为m=,所以.
(2)
=,
因为a=27,b=16,所以原式=4×2=6.
9.答案 2
解析 -2=4,又x>1,所以>0,所以=2.
10.答案
解析 利用一元二次方程根与系数的关系,得α+β=-2,αβ=,则2α·2β=2α+β=2-2=.
11.答案
解析 .
能力提升练
1.B 2.BD 3.C 5.B 6.ACD
1.B ∵a<.故选B.
2.BD =a5;
=a-4b6;
ac-2;
(-2=24y.故选BD.
3.答案 C
信息提取 ①A0,A1,A2,A3等,所有尺寸的纸张长宽比都为∶1;②以前一个序号的纸张的两条长边中点连线为折线对折裁剪分开后,可以得到两张后面序号大小的纸;③A0纸规格为84.1厘米×118.9厘米.
数学建模 由生活中常见纸张规格之间的长度关系建立与指数幂有关的数学模型,根据题意设出A4纸的长度,利用指数幂的运算法则求解.
解析 设A4纸的长度为x 厘米,则A3纸的长度为x 厘米,依此类推可以得到:)4=4,解得x≈29.7,故选C.
4.解析 (1)原式=(0.34-3-1×(34+π-3=π.
(2)原式==a2.
5.B ∵3α=5,3β=6,∴33α=53=125,32β=62=36,
∴=33α-2β.
6.ACD 因为a+a-1=4,所以a>0,a2+a-2=(a+a-1)2-2a·a-1=16-2=14,故A正确;
(a-a-1)2=a2+a-2-2a·a-1=12,所以a-a-1=±2,故B错误;
(=6,因为a>0,所以>0,所以,故C正确;
,故D正确.
7.答案
解析 由=4,即=4,得()2=a+a-1+2=16,所以a+a-1=14,
所以()2=a+a-1-2=12,因为a>1,所以,所以,
所以.
8.答案
解析 .因为3a+2b+1=0,所以,所以.
9.解析 (1)原式=
=.
将a=-代入,得原式=.
(2)由题意得(x-y)2=(x+y)2-4xy=64-36=28,
∵x>y>0,∴x-y=2.
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
