2025人教B版高中数学必修第二册同步练习题--5.1.4 用样本估计总体(含解析)
文档属性
| 名称 | 2025人教B版高中数学必修第二册同步练习题--5.1.4 用样本估计总体(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 587.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-19 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025人教B版高中数学必修第二册
5.1.4 用样本估计总体
基础过关练
题组一 用样本的数字特征估计总体的数字特征
1.某示范农场的鱼塘放养鱼苗8万条,根据这几年的经验知,鱼苗的成活率为95%,一段时间后准备打捞出售,第一网捞出40条,称得平均每条鱼2.5 kg,第二网捞出25条,称得平均每条鱼2.2 kg,第三网捞出35条,称得平均每条鱼2.8 kg,估计鱼塘中鱼的总质量为( )
A.192 280 kg B.202 280 kg
C.182 280 kg D.172 280 kg
2.(2023辽宁沈阳东北育才学校月考)某农业科学研究所为对比研究海水稻与普通水稻的根系深度,分别抽取了试验田中的海水稻以及对照田中的普通水稻各10株,测量了它们的根系深度(单位:cm),得到了如图所示的茎叶图,用样本估计总体,则下列结论中不正确的是 ( )
A.海水稻根系深度的中位数是45.5 cm
B.普通水稻根系深度的众数是32 cm
C.海水稻根系深度的平均数大于普通水稻根系深度的平均数
D.普通水稻根系深度的方差小于海水稻根系深度的方差
3.(2024湖南长沙期中)某高校在2023年新增设的“人工智能”专业共招收了两个班,其中甲班30人,乙班40人,在2023年高考中,甲班学生的平均分为665分,方差为131,乙班学生的平均分为658分,方差为208,则该专业所有学生在2023年高考中的平均分和方差分别为( )
A.661.5分,169.5 B.661分,187
C.661分,175 D.660分,180
题组二 用样本的分布估计总体的分布
4.某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩(总分为100分)分成六组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],得到如图所示的频率分布直方图.已知不及格(60分以下)的人数比优秀(不低于90分)的人数多60,则高一年级共有学生( )
A.300人 B.600人 C.200人 D.700人
5.(2022广东揭阳普宁华美实验学校月考)某校为了解高二年级学生某次数学考试成绩(单位:分)的分布情况,从该年级的1 120名学生中随机抽取了100名学生,了解他们的数学成绩,发现都在[80,150]内,现将这100名学生的成绩按照 [80,90),[90,100),[100,110),[110,120),[120,130),[130,140),[140,150]分组后,得到如图所示的频率分布直方图,则下列说法正确的是( )
A.a的值为0.04
B.样本中成绩低于130分的频率为 0.3
C.总体成绩的中位数(保留1位小数)大约为123.3分
D.总体成绩分布在[90,100)内的频数一定与总体成绩分布在[100,110)内的频数相等
6.(2022湖南长沙雅礼中学期中)某中学(含初、高中6个年级)随机选取了40名男生,将他们的身高(单位:cm)作为样本进行统计,得到如图所示的频率分布直方图.
(1)求a的值及样本中男生身高在[185,195]内的人数;
(2)估计该校男生身高的85%分位数.
7.(2024四川凉山期末)某市对该市常住居民用水情况进行了抽样调查,获得了该市常住居民去年100个家庭的月均用水量(单位:吨),将数据按照[1.0,1.5),[1.5,2.0),[2.0,2.5),…,[4.0,4.5]分成7组,制成了如图所示的频率分布直方图.
(1)求a的值;
(2)估计该市常住居民家庭月均用水量的中位数;
(3)若该市常住居民有15万个家庭,估计全市常住居民中月均用水量不低于3吨的家庭数,并说明理由.
能力提升练
题组一 用样本的数字特征估计总体的数字特征
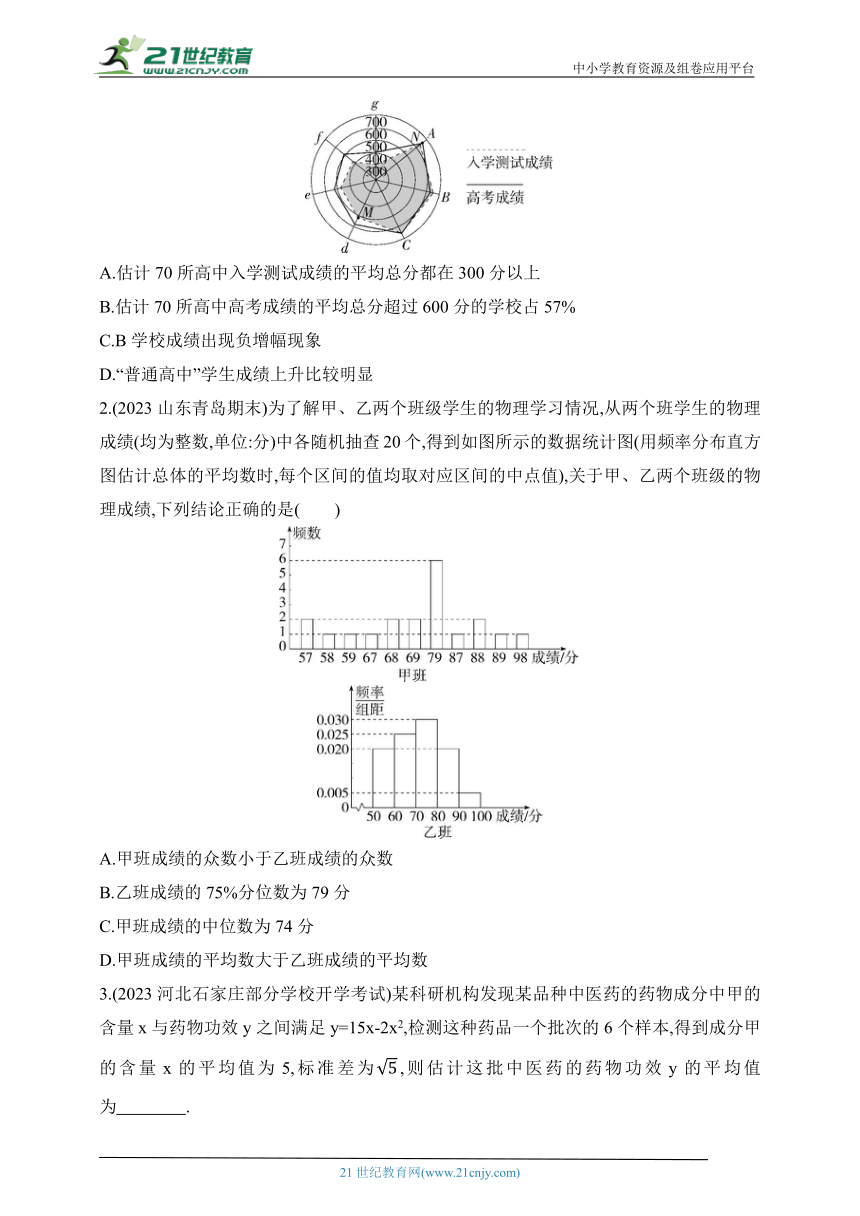
1.(2024辽宁葫芦岛期末)某市教育评价部门对本市70所高中按照分层抽样的方式抽出7所(其中“重点高中”3所,分别记为A,B,C,“普通高中”4所,分别记为d,e,f,g)进行跟踪统计分析,对7所高中的新生进行了统一入学测试,高考后,该市教育评价部门将各校的入学测试成绩的平均总分与高考成绩的平均总分绘制成了雷达图,如图.M点表示d学校入学测试成绩的平均总分大约为520分,N点表示A学校高考成绩的平均总分大约为660分,则下列叙述不正确的是( )
A.估计70所高中入学测试成绩的平均总分都在300分以上
B.估计70所高中高考成绩的平均总分超过600分的学校占57%
C.B学校成绩出现负增幅现象
D.“普通高中”学生成绩上升比较明显
2.(2023山东青岛期末)为了解甲、乙两个班级学生的物理学习情况,从两个班学生的物理成绩(均为整数,单位:分)中各随机抽查20个,得到如图所示的数据统计图(用频率分布直方图估计总体的平均数时,每个区间的值均取对应区间的中点值),关于甲、乙两个班级的物理成绩,下列结论正确的是( )
A.甲班成绩的众数小于乙班成绩的众数
B.乙班成绩的75%分位数为79分
C.甲班成绩的中位数为74分
D.甲班成绩的平均数大于乙班成绩的平均数
3.(2023河北石家庄部分学校开学考试)某科研机构发现某品种中医药的药物成分中甲的含量x与药物功效y之间满足y=15x-2x2,检测这种药品一个批次的6个样本,得到成分甲的含量x的平均值为5,标准差为,则估计这批中医药的药物功效y的平均值为 .
题组二 用样本的分布估计总体的分布
4.(多选题)(2024江苏南通期中)教育部《关于进一步加强中小学生体质健康管理工作的通知》中指出:各地要加强对学生体质健康重要性的宣传,让家长和中小学生科学认识体质健康的影响因素.提高学生体育与健康素养,增强体质健康管理的意识和能力.某学校共有2 000名男生,为了了解该校男生的身体发育情况,随机抽查了100名男生的体重情况.根据所得数据绘制样本的频率分布直方图如图所示(同一组中的数据用该组区间的中点值作代表),则下列结论正确的是( )
A.样本数据的众数为67.5
B.样本数据的80%分位数为72.5
C.样本数据的平均值为66
D.该校男生中体重低于60 kg的学生大约有300人
5.(2022四川成都期末)某学校举办了一场党史知识竞赛活动,共有500名学生参加.为了解本次知识竞赛活动的成绩,从中抽取了50名学生的分数(分数均为整数,满分为100分)进行统计,所有学生的分数都不低于60,将这50名学生的分数进行分组,第一组[60,70),第二组[70,80),第三组[80,90),第四组[90,100],得到如下的频率分布直方图.
(1)求m的值,并估计此次知识竞赛活动学生分数的中位数;
(2)根据频率分布直方图,估计此次知识竞赛活动学生分数的平均数.若对分数不低于平均数的同学进行奖励,请估计参赛的500名学生中获奖的人数.(同一组中的数据用该组区间的中点值作代表)
6.(2024四川成都外国语学校月考)某大学艺术专业400名学生参加某次测试,根据男、女学生的人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如图所示的频率分布直方图.
(1)估计400名学生中分数小于70的人数;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(3)根据该大学的规定,把15%的学生划定为不及格,利用(2)中的数据,确定本次测试的及格分数线.
答案与分层梯度式解析
5.1.4 用样本估计总体
基础过关练
1.A 2.D 3.B 4.B 5.C
1.A 依题意得鱼塘中的鱼的平均质量为=2.53(kg),
∴估计鱼塘中鱼的总质量为2.53×80 000×95%=192 280(kg).故选A.
2.D 由题中茎叶图,知海水稻根系深度的中位数是=45.5(cm),故A中结论正确;
普通水稻根系深度的众数是32 cm,故B中结论正确;
海水稻根系深度的平均数为×(38+39+39+43+44+47+49+50+50+51)=45(cm),普通水稻根系深度的平均数为×(25+27+32+32+34+36+38+40+41+45)=35(cm),故C中结论正确;
海水稻根系深度的方差为×[(38-45)2+(39-45)2+(39-45)2+(43-45)2+(44-45)2+(47-45)2+(49-45)2+(50-45)2+(50-45)2+(51-45)2]=23.2,普通水稻根系深度的方差为×[(25-35)2+(27-35)2+(32-35)2+(32-35)2+(34-35)2+(36-35)2+(38-35)2+(40-35)2+(41-35)2+(45-35)2]=35.4,故D中结论不正确.
3.B 设甲班的平均分为分,方差为,乙班的平均分为分,方差为,该专业所有学生的平均分为x分,方差为s.
由题意得=208,
所以=661,
s2=×[208+(658-661)2]=187.
4.B 由题图得不及格(60分以下)的学生的频率为(0.005+0.015)×10=0.2,优秀(不低于90分)的学生的频率为0.010×10=0.1.
设高一年级共有学生x人.由题意得(0.2-0.1)x=60,解得x=600.
故选B.
5.C 由题图得(0.005+0.010+0.010+0.015+a+0.025+0.005)×10=1,解得a=0.030,故A错误;
样本中成绩低于130分的频率为1-(0.025+0.005)×10=0.7,故B错误;
样本中成绩分布在[80,120)内的频率为(0.005+0.010+0.010+0.015)×10=0.4,
在[120,130)内的频率为0.030×10=0.3,
用样本估计总体,可估计总体成绩中的中位数为120+×10≈123.3(分),故C正确;
样本中成绩分布在[90,100)内的频数一定与样本中成绩分布在[100,110)内的频数相等,
但总体成绩分布在[90,100)内的频数不一定与总体成绩分布在[100,110)内的频数相等,故D错误.故选C.
6.解析 (1)根据题意得(0.005+a+0.020+0.025+0.040)×10=1,解得a=0.010,
所以样本中男生身高在[185,195]内的人数为40×0.010×10=4.
(2)因为(0.005+0.020+0.040)×10=0.65<0.85,
0.65+0.025×10=0.9>0.85,
所以样本数据的85%分位数落在[175,185)内,设其为x,则(x-175)×0.025=0.85-0.65,解得x=183,
所以估计该校男生身高的85%分位数为183 cm.
7.解析 (1)由题图知0.5×(0.1+a+0.4+0.5+0.4+0.3+0.1)=1,所以a=0.2.
(2)因为0.5×(0.1+0.2+0.4)=0.35<0.5,0.5×(0.1+0.2+0.4+0.5)=0.6>0.5,
所以月均用水量的中位数在[2.5,3.0)内,设样本数据的中位数为x,则0.35+(x-2.5)×0.5=0.5,解得x=2.8,
故该市常住居民家庭月均用水量的中位数为2.8吨.
(3)由题图知月均用水量不低于3吨的频率为0.5×(0.4+0.3+0.1)=0.4,
所以估计全市常住居民中月均用水量不低于3吨的家庭数为15×0.4=6(万个).
能力提升练
1.B 2.D 4.ABD
1.B 由题图可知,7所高中入学测试成绩的平均总分都在300分以上,用样本估计总体,知A中叙述正确;7所高中高考成绩的平均总分超过600分的学校有A,B,C三所,用样本估计总体,70所高中高考成绩的平均总分超过600分的学校占×100%≈43%,故B中叙述错误;B学校高考成绩的平均总分低于入学测试成绩的平均总分,故成绩出现负增幅现象,故C中叙述正确;“普通高中”高考成绩的平均总分都高于入学测试成绩的平均总分,故“普通高中”学生成绩上升比较明显,故D中叙述正确.故选B.
2.D 由题中甲、乙两个班级学生的物理成绩的数据统计图可知甲班成绩的众数为79分,乙班成绩的众数无法准确得出,A错误;
对于题中乙班物理成绩的频率分布直方图,
前三个矩形的面积之和为(0.020+0.025+0.030)×10=0.75,故乙班成绩的75%分位数为80分,B错误;
由题中甲班物理成绩的数据统计图可知,小于79分的数据有9个,等于79分的数据有6个,故甲班成绩的中位数为79分,C错误;
甲班成绩的平均数为
=74.8(分),
估计乙班成绩的平均数为10×(55×0.02+65×0.025+75×0.03+85×0.02+95×0.005)=71.5(分),71.5<
74.8,
即甲班成绩的平均数大于乙班成绩的平均数,D正确.故选D.
4.ABD 对于A,由题图得样本数据的众数为=67.5;
对于B,由于(0.03+0.05+0.06)×5=0.7<0.8,
(0.03+0.05+0.06+0.04)×5=0.9>0.8,
所以设样本数据的80%分位数为x,则0.7+(x-70)×0.04=0.8,∴x=72.5;
对于C,样本数据的平均值为57.5×0.15+62.5×0.25+67.5×0.3+72.5×0.2+77.5×0.1=66.75;
对于D,该校男生中体重低于60 kg的学生大约有2 000×0.03×5=300(人),故选ABD.
5.解析 (1)由题图知(0.01+m+0.04+0.02)×10=1,解得m=0.03.
设此次知识竞赛活动学生分数的中位数为x0,因为数据落在[60,80)内的频率为0.4,落在[60,90)内的频率为0.8,所以80(2)由题图及(1)知数据落在[60,70),[70,80),[80,90),[90,100]内的频率分别为0.1,0.3,0.4,0.2,则估计此次知识竞赛活动学生分数的平均数为65×0.1+75×0.3+85×0.4+95×0.2=82.
此次知识竞赛活动学生分数不低于82的频率为0.2+×0.4=0.52,则估计参赛的500名学生中获奖的人数为500×0.52=260.
6.解析 (1)根据题图可知,样本中分数不小于70的频率为(0.02+0.04)×10=0.6,所以样本中分数小于70的频率为1-0.6=0.4.
所以估计400名学生中分数小于70的人数为400×0.4=160.
(2)根据题图可知,样本中分数不小于50的频率为(0.01+0.02+0.04+0.02)×10=0.9,所以分数在区间[40,50)内的人数为100-100×0.9-5=5.
所以估计总体中分数在区间[40,50)内的人数为400×=20.
(3)设样本的15%分位数为x,结合(2)可知,分数小于50的频率为1-0.9=0.1,分数小于60的频率为0.1+0.1=0.2,所以x∈[50,60),由0.1+(x-50)×0.01=0.15,解得x=55,所以本次测试的及格分数线为55.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教B版高中数学必修第二册
5.1.4 用样本估计总体
基础过关练
题组一 用样本的数字特征估计总体的数字特征
1.某示范农场的鱼塘放养鱼苗8万条,根据这几年的经验知,鱼苗的成活率为95%,一段时间后准备打捞出售,第一网捞出40条,称得平均每条鱼2.5 kg,第二网捞出25条,称得平均每条鱼2.2 kg,第三网捞出35条,称得平均每条鱼2.8 kg,估计鱼塘中鱼的总质量为( )
A.192 280 kg B.202 280 kg
C.182 280 kg D.172 280 kg
2.(2023辽宁沈阳东北育才学校月考)某农业科学研究所为对比研究海水稻与普通水稻的根系深度,分别抽取了试验田中的海水稻以及对照田中的普通水稻各10株,测量了它们的根系深度(单位:cm),得到了如图所示的茎叶图,用样本估计总体,则下列结论中不正确的是 ( )
A.海水稻根系深度的中位数是45.5 cm
B.普通水稻根系深度的众数是32 cm
C.海水稻根系深度的平均数大于普通水稻根系深度的平均数
D.普通水稻根系深度的方差小于海水稻根系深度的方差
3.(2024湖南长沙期中)某高校在2023年新增设的“人工智能”专业共招收了两个班,其中甲班30人,乙班40人,在2023年高考中,甲班学生的平均分为665分,方差为131,乙班学生的平均分为658分,方差为208,则该专业所有学生在2023年高考中的平均分和方差分别为( )
A.661.5分,169.5 B.661分,187
C.661分,175 D.660分,180
题组二 用样本的分布估计总体的分布
4.某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩(总分为100分)分成六组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],得到如图所示的频率分布直方图.已知不及格(60分以下)的人数比优秀(不低于90分)的人数多60,则高一年级共有学生( )
A.300人 B.600人 C.200人 D.700人
5.(2022广东揭阳普宁华美实验学校月考)某校为了解高二年级学生某次数学考试成绩(单位:分)的分布情况,从该年级的1 120名学生中随机抽取了100名学生,了解他们的数学成绩,发现都在[80,150]内,现将这100名学生的成绩按照 [80,90),[90,100),[100,110),[110,120),[120,130),[130,140),[140,150]分组后,得到如图所示的频率分布直方图,则下列说法正确的是( )
A.a的值为0.04
B.样本中成绩低于130分的频率为 0.3
C.总体成绩的中位数(保留1位小数)大约为123.3分
D.总体成绩分布在[90,100)内的频数一定与总体成绩分布在[100,110)内的频数相等
6.(2022湖南长沙雅礼中学期中)某中学(含初、高中6个年级)随机选取了40名男生,将他们的身高(单位:cm)作为样本进行统计,得到如图所示的频率分布直方图.
(1)求a的值及样本中男生身高在[185,195]内的人数;
(2)估计该校男生身高的85%分位数.
7.(2024四川凉山期末)某市对该市常住居民用水情况进行了抽样调查,获得了该市常住居民去年100个家庭的月均用水量(单位:吨),将数据按照[1.0,1.5),[1.5,2.0),[2.0,2.5),…,[4.0,4.5]分成7组,制成了如图所示的频率分布直方图.
(1)求a的值;
(2)估计该市常住居民家庭月均用水量的中位数;
(3)若该市常住居民有15万个家庭,估计全市常住居民中月均用水量不低于3吨的家庭数,并说明理由.
能力提升练
题组一 用样本的数字特征估计总体的数字特征
1.(2024辽宁葫芦岛期末)某市教育评价部门对本市70所高中按照分层抽样的方式抽出7所(其中“重点高中”3所,分别记为A,B,C,“普通高中”4所,分别记为d,e,f,g)进行跟踪统计分析,对7所高中的新生进行了统一入学测试,高考后,该市教育评价部门将各校的入学测试成绩的平均总分与高考成绩的平均总分绘制成了雷达图,如图.M点表示d学校入学测试成绩的平均总分大约为520分,N点表示A学校高考成绩的平均总分大约为660分,则下列叙述不正确的是( )
A.估计70所高中入学测试成绩的平均总分都在300分以上
B.估计70所高中高考成绩的平均总分超过600分的学校占57%
C.B学校成绩出现负增幅现象
D.“普通高中”学生成绩上升比较明显
2.(2023山东青岛期末)为了解甲、乙两个班级学生的物理学习情况,从两个班学生的物理成绩(均为整数,单位:分)中各随机抽查20个,得到如图所示的数据统计图(用频率分布直方图估计总体的平均数时,每个区间的值均取对应区间的中点值),关于甲、乙两个班级的物理成绩,下列结论正确的是( )
A.甲班成绩的众数小于乙班成绩的众数
B.乙班成绩的75%分位数为79分
C.甲班成绩的中位数为74分
D.甲班成绩的平均数大于乙班成绩的平均数
3.(2023河北石家庄部分学校开学考试)某科研机构发现某品种中医药的药物成分中甲的含量x与药物功效y之间满足y=15x-2x2,检测这种药品一个批次的6个样本,得到成分甲的含量x的平均值为5,标准差为,则估计这批中医药的药物功效y的平均值为 .
题组二 用样本的分布估计总体的分布
4.(多选题)(2024江苏南通期中)教育部《关于进一步加强中小学生体质健康管理工作的通知》中指出:各地要加强对学生体质健康重要性的宣传,让家长和中小学生科学认识体质健康的影响因素.提高学生体育与健康素养,增强体质健康管理的意识和能力.某学校共有2 000名男生,为了了解该校男生的身体发育情况,随机抽查了100名男生的体重情况.根据所得数据绘制样本的频率分布直方图如图所示(同一组中的数据用该组区间的中点值作代表),则下列结论正确的是( )
A.样本数据的众数为67.5
B.样本数据的80%分位数为72.5
C.样本数据的平均值为66
D.该校男生中体重低于60 kg的学生大约有300人
5.(2022四川成都期末)某学校举办了一场党史知识竞赛活动,共有500名学生参加.为了解本次知识竞赛活动的成绩,从中抽取了50名学生的分数(分数均为整数,满分为100分)进行统计,所有学生的分数都不低于60,将这50名学生的分数进行分组,第一组[60,70),第二组[70,80),第三组[80,90),第四组[90,100],得到如下的频率分布直方图.
(1)求m的值,并估计此次知识竞赛活动学生分数的中位数;
(2)根据频率分布直方图,估计此次知识竞赛活动学生分数的平均数.若对分数不低于平均数的同学进行奖励,请估计参赛的500名学生中获奖的人数.(同一组中的数据用该组区间的中点值作代表)
6.(2024四川成都外国语学校月考)某大学艺术专业400名学生参加某次测试,根据男、女学生的人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如图所示的频率分布直方图.
(1)估计400名学生中分数小于70的人数;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(3)根据该大学的规定,把15%的学生划定为不及格,利用(2)中的数据,确定本次测试的及格分数线.
答案与分层梯度式解析
5.1.4 用样本估计总体
基础过关练
1.A 2.D 3.B 4.B 5.C
1.A 依题意得鱼塘中的鱼的平均质量为=2.53(kg),
∴估计鱼塘中鱼的总质量为2.53×80 000×95%=192 280(kg).故选A.
2.D 由题中茎叶图,知海水稻根系深度的中位数是=45.5(cm),故A中结论正确;
普通水稻根系深度的众数是32 cm,故B中结论正确;
海水稻根系深度的平均数为×(38+39+39+43+44+47+49+50+50+51)=45(cm),普通水稻根系深度的平均数为×(25+27+32+32+34+36+38+40+41+45)=35(cm),故C中结论正确;
海水稻根系深度的方差为×[(38-45)2+(39-45)2+(39-45)2+(43-45)2+(44-45)2+(47-45)2+(49-45)2+(50-45)2+(50-45)2+(51-45)2]=23.2,普通水稻根系深度的方差为×[(25-35)2+(27-35)2+(32-35)2+(32-35)2+(34-35)2+(36-35)2+(38-35)2+(40-35)2+(41-35)2+(45-35)2]=35.4,故D中结论不正确.
3.B 设甲班的平均分为分,方差为,乙班的平均分为分,方差为,该专业所有学生的平均分为x分,方差为s.
由题意得=208,
所以=661,
s2=×[208+(658-661)2]=187.
4.B 由题图得不及格(60分以下)的学生的频率为(0.005+0.015)×10=0.2,优秀(不低于90分)的学生的频率为0.010×10=0.1.
设高一年级共有学生x人.由题意得(0.2-0.1)x=60,解得x=600.
故选B.
5.C 由题图得(0.005+0.010+0.010+0.015+a+0.025+0.005)×10=1,解得a=0.030,故A错误;
样本中成绩低于130分的频率为1-(0.025+0.005)×10=0.7,故B错误;
样本中成绩分布在[80,120)内的频率为(0.005+0.010+0.010+0.015)×10=0.4,
在[120,130)内的频率为0.030×10=0.3,
用样本估计总体,可估计总体成绩中的中位数为120+×10≈123.3(分),故C正确;
样本中成绩分布在[90,100)内的频数一定与样本中成绩分布在[100,110)内的频数相等,
但总体成绩分布在[90,100)内的频数不一定与总体成绩分布在[100,110)内的频数相等,故D错误.故选C.
6.解析 (1)根据题意得(0.005+a+0.020+0.025+0.040)×10=1,解得a=0.010,
所以样本中男生身高在[185,195]内的人数为40×0.010×10=4.
(2)因为(0.005+0.020+0.040)×10=0.65<0.85,
0.65+0.025×10=0.9>0.85,
所以样本数据的85%分位数落在[175,185)内,设其为x,则(x-175)×0.025=0.85-0.65,解得x=183,
所以估计该校男生身高的85%分位数为183 cm.
7.解析 (1)由题图知0.5×(0.1+a+0.4+0.5+0.4+0.3+0.1)=1,所以a=0.2.
(2)因为0.5×(0.1+0.2+0.4)=0.35<0.5,0.5×(0.1+0.2+0.4+0.5)=0.6>0.5,
所以月均用水量的中位数在[2.5,3.0)内,设样本数据的中位数为x,则0.35+(x-2.5)×0.5=0.5,解得x=2.8,
故该市常住居民家庭月均用水量的中位数为2.8吨.
(3)由题图知月均用水量不低于3吨的频率为0.5×(0.4+0.3+0.1)=0.4,
所以估计全市常住居民中月均用水量不低于3吨的家庭数为15×0.4=6(万个).
能力提升练
1.B 2.D 4.ABD
1.B 由题图可知,7所高中入学测试成绩的平均总分都在300分以上,用样本估计总体,知A中叙述正确;7所高中高考成绩的平均总分超过600分的学校有A,B,C三所,用样本估计总体,70所高中高考成绩的平均总分超过600分的学校占×100%≈43%,故B中叙述错误;B学校高考成绩的平均总分低于入学测试成绩的平均总分,故成绩出现负增幅现象,故C中叙述正确;“普通高中”高考成绩的平均总分都高于入学测试成绩的平均总分,故“普通高中”学生成绩上升比较明显,故D中叙述正确.故选B.
2.D 由题中甲、乙两个班级学生的物理成绩的数据统计图可知甲班成绩的众数为79分,乙班成绩的众数无法准确得出,A错误;
对于题中乙班物理成绩的频率分布直方图,
前三个矩形的面积之和为(0.020+0.025+0.030)×10=0.75,故乙班成绩的75%分位数为80分,B错误;
由题中甲班物理成绩的数据统计图可知,小于79分的数据有9个,等于79分的数据有6个,故甲班成绩的中位数为79分,C错误;
甲班成绩的平均数为
=74.8(分),
估计乙班成绩的平均数为10×(55×0.02+65×0.025+75×0.03+85×0.02+95×0.005)=71.5(分),71.5<
74.8,
即甲班成绩的平均数大于乙班成绩的平均数,D正确.故选D.
4.ABD 对于A,由题图得样本数据的众数为=67.5;
对于B,由于(0.03+0.05+0.06)×5=0.7<0.8,
(0.03+0.05+0.06+0.04)×5=0.9>0.8,
所以设样本数据的80%分位数为x,则0.7+(x-70)×0.04=0.8,∴x=72.5;
对于C,样本数据的平均值为57.5×0.15+62.5×0.25+67.5×0.3+72.5×0.2+77.5×0.1=66.75;
对于D,该校男生中体重低于60 kg的学生大约有2 000×0.03×5=300(人),故选ABD.
5.解析 (1)由题图知(0.01+m+0.04+0.02)×10=1,解得m=0.03.
设此次知识竞赛活动学生分数的中位数为x0,因为数据落在[60,80)内的频率为0.4,落在[60,90)内的频率为0.8,所以80
此次知识竞赛活动学生分数不低于82的频率为0.2+×0.4=0.52,则估计参赛的500名学生中获奖的人数为500×0.52=260.
6.解析 (1)根据题图可知,样本中分数不小于70的频率为(0.02+0.04)×10=0.6,所以样本中分数小于70的频率为1-0.6=0.4.
所以估计400名学生中分数小于70的人数为400×0.4=160.
(2)根据题图可知,样本中分数不小于50的频率为(0.01+0.02+0.04+0.02)×10=0.9,所以分数在区间[40,50)内的人数为100-100×0.9-5=5.
所以估计总体中分数在区间[40,50)内的人数为400×=20.
(3)设样本的15%分位数为x,结合(2)可知,分数小于50的频率为1-0.9=0.1,分数小于60的频率为0.1+0.1=0.2,所以x∈[50,60),由0.1+(x-50)×0.01=0.15,解得x=55,所以本次测试的及格分数线为55.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
