2025人教B版高中数学必修第一册同步练习题--3.1.2第1课时 函数的单调性(含解析)
文档属性
| 名称 | 2025人教B版高中数学必修第一册同步练习题--3.1.2第1课时 函数的单调性(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 452.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-19 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025人教B版高中数学必修第一册
3.1.2 函数的单调性
第1课时 函数的单调性
基础过关练
题组一 单调性的判断与证明
1.(2024江西上饶期末)下图是函数y=f(x)的图象,则函数f(x)的单调递减区间为( )
A.(-2,0) B.(-2,2) C.(0,2) D.(2,+∞)
2.已知函数f(x)在R上是增函数,则下列说法正确的是( )
A.y=-f(x)在R上是减函数
B.y=在R上是减函数
C.y=[f(x)]2在R上是增函数
D.y=af(x)(a为实数)在R上是增函数
3.(2023北京西城期中)下列函数中,在区间(0,+∞)上是增函数的是( )
A.y=x2-2x B.y=-2x+1
C.y=|x| D.y=-
4.(2024陕西汉中期末)已知函数f(x)=, f(1)=, f(0)=0.
(1)求f(x)的解析式;
(2)试判断函数f(x)在(-∞,-2)上的单调性,并利用定义给予证明.
题组二 函数的平均变化率
5.(2024湖南株洲期末)已知函数f(x)的定义域为D,区间I D,设Δx=x1-x2,Δy=f(x1)-f(x2),其中x1≠x2,则“ x1,x2∈I,>0”是“函数f(x)在区间I上单调递增”的( )
A.充分必要条件
B.必要不充分条件
C.充分不必要条件
D.既不充分也不必要条件
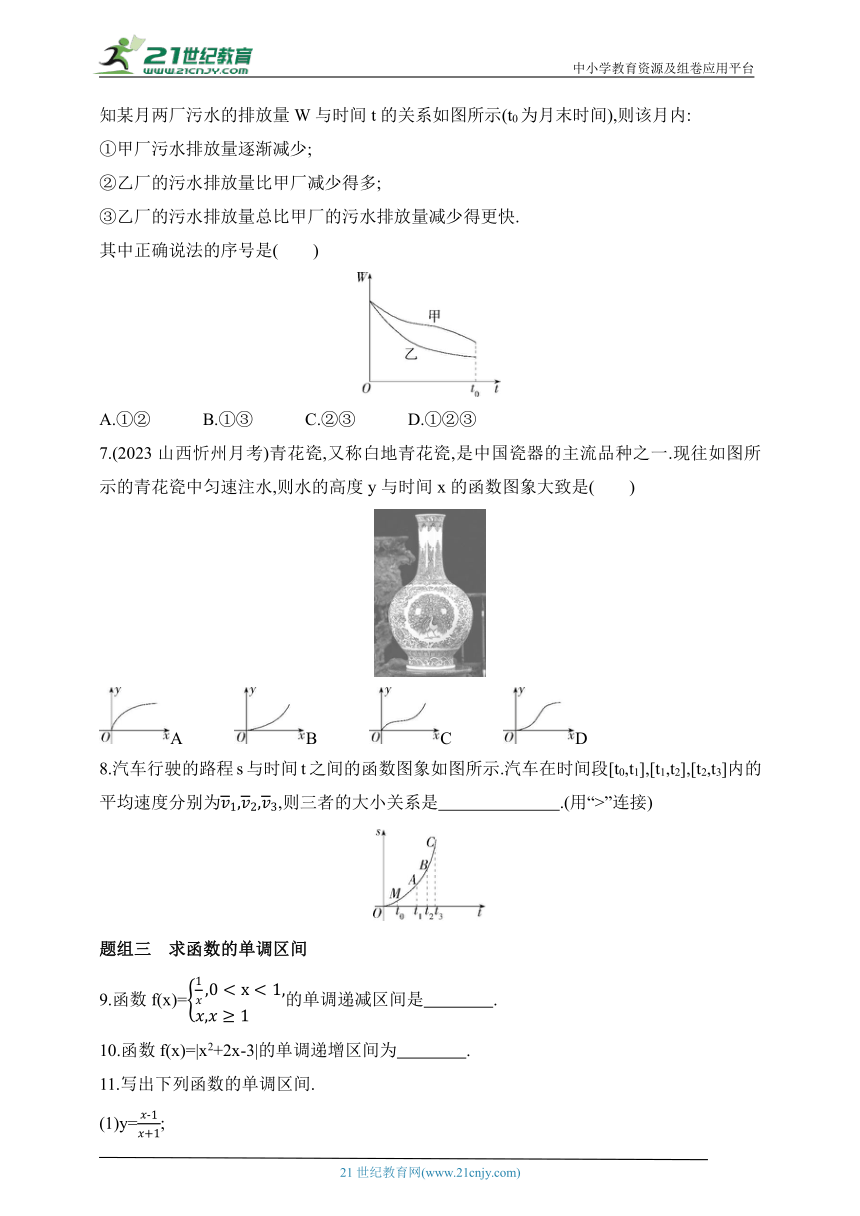
6.(2023广东揭阳期末)为响应国家节能减排号召,甲、乙两个工厂进行了污水排放治理,已知某月两厂污水的排放量W与时间t的关系如图所示(t0为月末时间),则该月内:
①甲厂污水排放量逐渐减少;
②乙厂的污水排放量比甲厂减少得多;
③乙厂的污水排放量总比甲厂的污水排放量减少得更快.
其中正确说法的序号是( )
A.①② B.①③ C.②③ D.①②③
7.(2023山西忻州月考)青花瓷,又称白地青花瓷,是中国瓷器的主流品种之一.现往如图所示的青花瓷中匀速注水,则水的高度y与时间x的函数图象大致是( )
A B C D
8.汽车行驶的路程s与时间t之间的函数图象如图所示.汽车在时间段[t0,t1],[t1,t2],[t2,t3]内的平均速度分别为,则三者的大小关系是 .(用“>”连接)
题组三 求函数的单调区间
9.函数f(x)=的单调递减区间是 .
10.函数f(x)=|x2+2x-3|的单调递增区间为 .
11.写出下列函数的单调区间.
(1)y=;
(2)y=
(3)y=-x2+2|x|+3.
题组四 函数的最值
12.(2024江西南昌期末)已知函数f(x)=x2-2x+3,则f(x)在区间[0,4]上的值域为( )
A.[3,6] B.[2,6] C.[2,11] D.[3,11]
13.(2024四川达州期末)已知函数f(x)=则f(x)的最大值是( )
A.60 B.58 C.56 D.52
14.(2024江西抚州期末)函数y=在区间[2,4]上的值域为( )
A.[-3,5]
B.[-5,3]
C.(-∞,-3)∪(5,+∞)
D.(-∞,-3]∪[5,+∞)
15.(2024辽宁朝阳期末)已知函数f(x)=满足f(1)=-, f(3)=.
(1)求函数f(x)的解析式;
(2)求函数f(x)在[2,4]上的值域.
能力提升练
题组一 单调性的判断
1.下列函数中,在区间(1,+∞)上为增函数的是( )
A.y=-3x-1 B.y= C.y=x2-4x+5 D.y=|x-1|+2
2.(多选题)(2024广东江门期末)已知函数f(x)=,则( )
A.f(x)的定义域为{x|x≠-1}
B.f(x)+f=2(x≠0)
C.f(x)在区间(-1,+∞)上单调递增
D.f(x)的值域为R
题组二 函数的最值
3.(2024江苏南通期末)函数y=|x-2|+|2x-2|的最小值为( )
A.0 B.1 C. D.2
4.(2023河南信阳期末)函数f(x)=x(|x|-1)在[m,n]上的最小值为-,最大值为2,则n-m的最大值为( )
A. C. D.2
5.(多选题)(2023辽宁辽西联合校期中)对于实数x,[x]表示不超过x的最大整数,例如[π]=3,[-1.5]=-2,定义函数f(x)=x-[x],则下列命题中正确的是( )
A.f(-3.9)=f(4.1)
B.函数f(x)的最大值为1
C.函数f(x)的最小值为0
D.方程f(x)-=0有无数个根
6.(多选题)(2022江苏镇江中学调研)已知函数f(x)=-2x+1(x∈[-2,2]),g(x)=x2-2x(x∈[0,3]),则下列结论正确的是( )
A. x∈[-2,2], f(x)>a恒成立,则实数a的取值范围是(-∞,-3)
B. x∈[-2,2], f(x)>a,则实数a的取值范围是(-∞,-3)
C. x∈[0,3],g(x)=a,则实数a的取值范围是[-1,3]
D. x∈[-2,2], t∈[0,3],使f(x)=g(t)
7.(2022河北师大附中期中)记实数x1,x2,…,xn中的最小数为min{x1,x2,…,xn},若f(x)=min{x+1,x2-x+1,-x+6},则函数f(x)的最大值为 .
8.设f(x)=x2-2ax+a2,x∈[0,2],当a=-1时, f(x)的最小值是 ,若f(0)是f(x)的最小值,则a的取值范围为 .
9.(2024吉林长春期末)已知函数f(x)=x-,x∈[1,2].
(1)判断f(x)的单调性,并利用单调性的定义加以证明;
(2)设F(x)=x2+,x∈[1,2],求函数F(x)的最小值g(a).
答案与分层梯度式解析
3.1.2 函数的单调性
第1课时 函数的单调性
基础过关练
1.C 2.A 3.C 5.A 6.A 7.C 12.C 13.C
14.D
1.C 由题图可得,函数f(x)的单调递减区间为(0,2).
2.A 任取x1,x2∈R,且x1-f(x2),故y=-f(x)在R上是减函数,A正确;当f(x)=x时,y=在(-∞,0),(0,+∞)上单调递减,y=[f(x)]2=x2在(-∞,0)上单调递减,在(0,+∞)上单调递增,故B,C错误;当a≤0时,y=af(x)不是R上的增函数,D错误.
3.C A中,y=x2-2x的图象开口向上,对称轴为直线x=1,所以该函数在(0,1)上单调递减,在(1,+∞)上单调递增,不符合题意;B中,y=-2x+1在(0,+∞)上是减函数,不符合题意;C中,y=|x|=在(0,+∞)上是增函数,符合题意;D中,因为y=在(0,+∞)上是增函数,所以y=-在(0,+∞)上是减函数,不符合题意.故选C.
4.解析 (1)由题意得,
∴f(x)=.
(2)f(x)在(-∞,-2)上单调递增.
证明:任取x1,x2∈(-∞,-2)且x1则f(x1)-f(x2)=
=,
∵x1+2<0,x2+2<0,x1-x2<0,∴<0,
∴f(x1)-f(x2)<0,即f(x1)故f(x)在(-∞,-2)上单调递增.
5.A 函数f(x)在区间I上单调递增的充要条件是 x1,x2∈I,当x1>x2时,都有f(x1)>f(x2),或当x1即 x1,x2∈I,x1-x2与f(x1)-f(x2)同号,也即 x1,x2∈I,>0.
6.A 易知①②正确;因为后期甲厂污水排放量的变化率大于乙厂污水排放量的变化率,所以③不正确.故选A.
7.C 由题图可知,青花瓷上、下细,中间粗,则水的高度的变化为快—慢—快,结合选项可知,C符合题意.
8.答案
9.答案 (0,1]
解析 函数f(x)的图象如图所示.
由图象可知, f(x)的单调递减区间是(0,1].
10.答案 (-3,-1),(1,+∞)
解析 令g(x)=x2+2x-3=(x+1)2-4.作出g(x)的图象,保留其在x轴及x轴上方的图象,再把它在x轴下方的图象翻折到x轴上方,就得到f(x)=|x2+2x-3|的图象,如图所示.
由图象易得函数f(x)的单调递增区间是(-3,-1),(1,+∞).
11.解析 (1)y=,函数在(-∞,-1)和(-1,+∞)上单调递增.
(2)作出函数y=的图象如图所示,
由图可知,函数的单调递增区间为(0,+∞),单调递减区间为(-∞,0].
(3)y=-x2+2|x|+3=作出函数的图象如图所示,
由图可知,函数的单调递增区间为(-∞,-1)和(0,1),单调递减区间为(-1,0)和(1,+∞).
12.C 因为f(x)=x2-2x+3=(x-1)2+2,所以f(x)在(0,1)上单调递减,在(1,4)上单调递增,
又f(1)=2, f(0)=3, f(4)=11,所以f(x)在区间[0,4]上的值域为[2,11].
13.C 当0≤x<8时, f(x)=-x2+12x+20=-(x-6)2+56,所以f(x)max=f(6)=56;当x≥8时, f(x)=46+在[8,+∞)上单调递减,所以f(x)max=f(8)=52.
综上所述, f(x)max=f(6)=56.
14.D 函数y=,易得函数的定义域为{x|x≠3},函数在[2,3)上单调递减,在(3,4]上单调递减,当x=2时,y=-3;当x=4时,y=5.所以函数的值域为(-∞,-3]∪[5,+∞).
15.解析 (1)因为f(x)=, f(1)=-, f(3)=,
所以故f(x)=.
(2)由(1)可知f(x)=,其定义域为(-∞,0)∪(0,+∞),
因为函数y=与y=-在[2,4]上均单调递增,
所以函数f(x)=在[2,4]上单调递增.
又f(2)=, f(4)=,
所以函数f(x)在[2,4]上的值域为.
能力提升练
1.D 2.ABC 3.B 4.B 5.ACD 6.AC
1.D 由一次函数的性质可知,y=-3x-1在区间(1,+∞)上为减函数,故A错误;
由反比例函数的性质可知,y=在区间(1,+∞)上为减函数,故B错误;
由二次函数的性质可知,y=x2-4x+5在(-∞,2)上单调递减,在(2,+∞)上单调递增,故C错误;
对于D,当x>1时,y=x+1,函数在(1,+∞)上单调递增,故D正确.故选D.
2.ABC 由函数f(x)=,可知x+1≠0,解得x≠-1,所以函数的定义域为{x|x≠-1},故A正确;f(x)+f=2,故B正确;因为f(x)=,所以当x∈(-1,+∞)时, f(x)单调递增,故C正确;由f(x)=2-可知, f(x)≠2,故函数f(x)的值域不为R,故D错误.
3.B y=|x-2|+|2x-2|=
画出函数y=|x-2|+|2x-2|的图象,如图所示,
由图可知,当x=1时,ymin=1.
4.B 当x≥0时, f(x)=x(|x|-1)=x2-x,当x<0时,f(x)=x(|x|-1)=-x2-x,作出函数f(x)的图象如图所示,
当x≥0时,令f(x)=x2-x=2,解得x=2.令f(x)=x2-x=-,得x=.
当x<0时,令f(x)=-x2-x=-,则4x2+4x-1=0,解得x=.
∵f(x)在[m,n]上的最小值为-,最大值为2,∴n=2,≤m≤,∴n-m的最大值为2-,故选B.
5.ACD 当-1≤x<0时,[x]=-1,则f(x)=x+1;当0≤x<1时,[x]=0,则f(x)=x;当1≤x<2时,[x]=1,则f(x)=x-1;当2≤x<3时,[x]=2,则f(x)=x-2;……
画出函数f(x)=x-[x]的图象如图所示.
对于A,f(-3.9)=-3.9-(-4)=0.1, f(4.1)=4.1-4=0.1,所以f(-3.9)=f(4.1),故A正确;对于B,C,由图象可知,函数f(x)=x-[x]的值域为[0,1),故B错误,C正确;对于D,易知y=f(x)的图象与直线y=有无数个交点,故方程f(x)-=0有无数个根,故D正确.故选ACD.
6.AC 对于A,由题意得a7.答案
解析 画出函数f(x)的图象,如图中实线部分所示.
由图可知, f(x)的最大值为.
8.答案 1;(-∞,0]
解析 当a=-1时, f(x)=x2+2x+1,易知y=x2+2x+1的图象开口向上,对称轴为直线x=-1,所以函数f(x)=x2+2x+1在[0,2]上单调递增,所以函数f(x)的最小值为f(0)=1.
若f(0)是f(x)的最小值,则直线x=a在y轴左侧或与y轴重合,故a≤0,所以a的取值范围为(-∞,0].
9.解析 (1)函数f(x)在[1,2]上单调递增,证明如下:任取x1,x2∈[1,2],且x1则f(x1)-f(x2)=x1-,
因为x1,x2∈[1,2],且x10,
所以f(x1)-f(x2)<0,即f(x1)(2)因为函数f(x)在[1,2]上单调递增,且f(1)=-3, f(2)=0,所以f(x)在[1,2]上的值域为[-3,0].
设t=x-,x∈[1,2],则t∈[-3,0],
设h(t)=t2-2at+8,t∈[-3,0],易知函数y=t2-2at+8的图象的对称轴为直线t=a,所以当a≤-3时,函数h(t)在[-3,0]上单调递增,
所以g(a)=h(-3)=17+6a;
当-3当a≥0时,函数h(t)在[-3,0]上单调递减,g(a)=h(0)=8.
故g(a)=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教B版高中数学必修第一册
3.1.2 函数的单调性
第1课时 函数的单调性
基础过关练
题组一 单调性的判断与证明
1.(2024江西上饶期末)下图是函数y=f(x)的图象,则函数f(x)的单调递减区间为( )
A.(-2,0) B.(-2,2) C.(0,2) D.(2,+∞)
2.已知函数f(x)在R上是增函数,则下列说法正确的是( )
A.y=-f(x)在R上是减函数
B.y=在R上是减函数
C.y=[f(x)]2在R上是增函数
D.y=af(x)(a为实数)在R上是增函数
3.(2023北京西城期中)下列函数中,在区间(0,+∞)上是增函数的是( )
A.y=x2-2x B.y=-2x+1
C.y=|x| D.y=-
4.(2024陕西汉中期末)已知函数f(x)=, f(1)=, f(0)=0.
(1)求f(x)的解析式;
(2)试判断函数f(x)在(-∞,-2)上的单调性,并利用定义给予证明.
题组二 函数的平均变化率
5.(2024湖南株洲期末)已知函数f(x)的定义域为D,区间I D,设Δx=x1-x2,Δy=f(x1)-f(x2),其中x1≠x2,则“ x1,x2∈I,>0”是“函数f(x)在区间I上单调递增”的( )
A.充分必要条件
B.必要不充分条件
C.充分不必要条件
D.既不充分也不必要条件
6.(2023广东揭阳期末)为响应国家节能减排号召,甲、乙两个工厂进行了污水排放治理,已知某月两厂污水的排放量W与时间t的关系如图所示(t0为月末时间),则该月内:
①甲厂污水排放量逐渐减少;
②乙厂的污水排放量比甲厂减少得多;
③乙厂的污水排放量总比甲厂的污水排放量减少得更快.
其中正确说法的序号是( )
A.①② B.①③ C.②③ D.①②③
7.(2023山西忻州月考)青花瓷,又称白地青花瓷,是中国瓷器的主流品种之一.现往如图所示的青花瓷中匀速注水,则水的高度y与时间x的函数图象大致是( )
A B C D
8.汽车行驶的路程s与时间t之间的函数图象如图所示.汽车在时间段[t0,t1],[t1,t2],[t2,t3]内的平均速度分别为,则三者的大小关系是 .(用“>”连接)
题组三 求函数的单调区间
9.函数f(x)=的单调递减区间是 .
10.函数f(x)=|x2+2x-3|的单调递增区间为 .
11.写出下列函数的单调区间.
(1)y=;
(2)y=
(3)y=-x2+2|x|+3.
题组四 函数的最值
12.(2024江西南昌期末)已知函数f(x)=x2-2x+3,则f(x)在区间[0,4]上的值域为( )
A.[3,6] B.[2,6] C.[2,11] D.[3,11]
13.(2024四川达州期末)已知函数f(x)=则f(x)的最大值是( )
A.60 B.58 C.56 D.52
14.(2024江西抚州期末)函数y=在区间[2,4]上的值域为( )
A.[-3,5]
B.[-5,3]
C.(-∞,-3)∪(5,+∞)
D.(-∞,-3]∪[5,+∞)
15.(2024辽宁朝阳期末)已知函数f(x)=满足f(1)=-, f(3)=.
(1)求函数f(x)的解析式;
(2)求函数f(x)在[2,4]上的值域.
能力提升练
题组一 单调性的判断
1.下列函数中,在区间(1,+∞)上为增函数的是( )
A.y=-3x-1 B.y= C.y=x2-4x+5 D.y=|x-1|+2
2.(多选题)(2024广东江门期末)已知函数f(x)=,则( )
A.f(x)的定义域为{x|x≠-1}
B.f(x)+f=2(x≠0)
C.f(x)在区间(-1,+∞)上单调递增
D.f(x)的值域为R
题组二 函数的最值
3.(2024江苏南通期末)函数y=|x-2|+|2x-2|的最小值为( )
A.0 B.1 C. D.2
4.(2023河南信阳期末)函数f(x)=x(|x|-1)在[m,n]上的最小值为-,最大值为2,则n-m的最大值为( )
A. C. D.2
5.(多选题)(2023辽宁辽西联合校期中)对于实数x,[x]表示不超过x的最大整数,例如[π]=3,[-1.5]=-2,定义函数f(x)=x-[x],则下列命题中正确的是( )
A.f(-3.9)=f(4.1)
B.函数f(x)的最大值为1
C.函数f(x)的最小值为0
D.方程f(x)-=0有无数个根
6.(多选题)(2022江苏镇江中学调研)已知函数f(x)=-2x+1(x∈[-2,2]),g(x)=x2-2x(x∈[0,3]),则下列结论正确的是( )
A. x∈[-2,2], f(x)>a恒成立,则实数a的取值范围是(-∞,-3)
B. x∈[-2,2], f(x)>a,则实数a的取值范围是(-∞,-3)
C. x∈[0,3],g(x)=a,则实数a的取值范围是[-1,3]
D. x∈[-2,2], t∈[0,3],使f(x)=g(t)
7.(2022河北师大附中期中)记实数x1,x2,…,xn中的最小数为min{x1,x2,…,xn},若f(x)=min{x+1,x2-x+1,-x+6},则函数f(x)的最大值为 .
8.设f(x)=x2-2ax+a2,x∈[0,2],当a=-1时, f(x)的最小值是 ,若f(0)是f(x)的最小值,则a的取值范围为 .
9.(2024吉林长春期末)已知函数f(x)=x-,x∈[1,2].
(1)判断f(x)的单调性,并利用单调性的定义加以证明;
(2)设F(x)=x2+,x∈[1,2],求函数F(x)的最小值g(a).
答案与分层梯度式解析
3.1.2 函数的单调性
第1课时 函数的单调性
基础过关练
1.C 2.A 3.C 5.A 6.A 7.C 12.C 13.C
14.D
1.C 由题图可得,函数f(x)的单调递减区间为(0,2).
2.A 任取x1,x2∈R,且x1
3.C A中,y=x2-2x的图象开口向上,对称轴为直线x=1,所以该函数在(0,1)上单调递减,在(1,+∞)上单调递增,不符合题意;B中,y=-2x+1在(0,+∞)上是减函数,不符合题意;C中,y=|x|=在(0,+∞)上是增函数,符合题意;D中,因为y=在(0,+∞)上是增函数,所以y=-在(0,+∞)上是减函数,不符合题意.故选C.
4.解析 (1)由题意得,
∴f(x)=.
(2)f(x)在(-∞,-2)上单调递增.
证明:任取x1,x2∈(-∞,-2)且x1
=,
∵x1+2<0,x2+2<0,x1-x2<0,∴<0,
∴f(x1)-f(x2)<0,即f(x1)
5.A 函数f(x)在区间I上单调递增的充要条件是 x1,x2∈I,当x1>x2时,都有f(x1)>f(x2),或当x1
6.A 易知①②正确;因为后期甲厂污水排放量的变化率大于乙厂污水排放量的变化率,所以③不正确.故选A.
7.C 由题图可知,青花瓷上、下细,中间粗,则水的高度的变化为快—慢—快,结合选项可知,C符合题意.
8.答案
9.答案 (0,1]
解析 函数f(x)的图象如图所示.
由图象可知, f(x)的单调递减区间是(0,1].
10.答案 (-3,-1),(1,+∞)
解析 令g(x)=x2+2x-3=(x+1)2-4.作出g(x)的图象,保留其在x轴及x轴上方的图象,再把它在x轴下方的图象翻折到x轴上方,就得到f(x)=|x2+2x-3|的图象,如图所示.
由图象易得函数f(x)的单调递增区间是(-3,-1),(1,+∞).
11.解析 (1)y=,函数在(-∞,-1)和(-1,+∞)上单调递增.
(2)作出函数y=的图象如图所示,
由图可知,函数的单调递增区间为(0,+∞),单调递减区间为(-∞,0].
(3)y=-x2+2|x|+3=作出函数的图象如图所示,
由图可知,函数的单调递增区间为(-∞,-1)和(0,1),单调递减区间为(-1,0)和(1,+∞).
12.C 因为f(x)=x2-2x+3=(x-1)2+2,所以f(x)在(0,1)上单调递减,在(1,4)上单调递增,
又f(1)=2, f(0)=3, f(4)=11,所以f(x)在区间[0,4]上的值域为[2,11].
13.C 当0≤x<8时, f(x)=-x2+12x+20=-(x-6)2+56,所以f(x)max=f(6)=56;当x≥8时, f(x)=46+在[8,+∞)上单调递减,所以f(x)max=f(8)=52.
综上所述, f(x)max=f(6)=56.
14.D 函数y=,易得函数的定义域为{x|x≠3},函数在[2,3)上单调递减,在(3,4]上单调递减,当x=2时,y=-3;当x=4时,y=5.所以函数的值域为(-∞,-3]∪[5,+∞).
15.解析 (1)因为f(x)=, f(1)=-, f(3)=,
所以故f(x)=.
(2)由(1)可知f(x)=,其定义域为(-∞,0)∪(0,+∞),
因为函数y=与y=-在[2,4]上均单调递增,
所以函数f(x)=在[2,4]上单调递增.
又f(2)=, f(4)=,
所以函数f(x)在[2,4]上的值域为.
能力提升练
1.D 2.ABC 3.B 4.B 5.ACD 6.AC
1.D 由一次函数的性质可知,y=-3x-1在区间(1,+∞)上为减函数,故A错误;
由反比例函数的性质可知,y=在区间(1,+∞)上为减函数,故B错误;
由二次函数的性质可知,y=x2-4x+5在(-∞,2)上单调递减,在(2,+∞)上单调递增,故C错误;
对于D,当x>1时,y=x+1,函数在(1,+∞)上单调递增,故D正确.故选D.
2.ABC 由函数f(x)=,可知x+1≠0,解得x≠-1,所以函数的定义域为{x|x≠-1},故A正确;f(x)+f=2,故B正确;因为f(x)=,所以当x∈(-1,+∞)时, f(x)单调递增,故C正确;由f(x)=2-可知, f(x)≠2,故函数f(x)的值域不为R,故D错误.
3.B y=|x-2|+|2x-2|=
画出函数y=|x-2|+|2x-2|的图象,如图所示,
由图可知,当x=1时,ymin=1.
4.B 当x≥0时, f(x)=x(|x|-1)=x2-x,当x<0时,f(x)=x(|x|-1)=-x2-x,作出函数f(x)的图象如图所示,
当x≥0时,令f(x)=x2-x=2,解得x=2.令f(x)=x2-x=-,得x=.
当x<0时,令f(x)=-x2-x=-,则4x2+4x-1=0,解得x=.
∵f(x)在[m,n]上的最小值为-,最大值为2,∴n=2,≤m≤,∴n-m的最大值为2-,故选B.
5.ACD 当-1≤x<0时,[x]=-1,则f(x)=x+1;当0≤x<1时,[x]=0,则f(x)=x;当1≤x<2时,[x]=1,则f(x)=x-1;当2≤x<3时,[x]=2,则f(x)=x-2;……
画出函数f(x)=x-[x]的图象如图所示.
对于A,f(-3.9)=-3.9-(-4)=0.1, f(4.1)=4.1-4=0.1,所以f(-3.9)=f(4.1),故A正确;对于B,C,由图象可知,函数f(x)=x-[x]的值域为[0,1),故B错误,C正确;对于D,易知y=f(x)的图象与直线y=有无数个交点,故方程f(x)-=0有无数个根,故D正确.故选ACD.
6.AC 对于A,由题意得a
解析 画出函数f(x)的图象,如图中实线部分所示.
由图可知, f(x)的最大值为.
8.答案 1;(-∞,0]
解析 当a=-1时, f(x)=x2+2x+1,易知y=x2+2x+1的图象开口向上,对称轴为直线x=-1,所以函数f(x)=x2+2x+1在[0,2]上单调递增,所以函数f(x)的最小值为f(0)=1.
若f(0)是f(x)的最小值,则直线x=a在y轴左侧或与y轴重合,故a≤0,所以a的取值范围为(-∞,0].
9.解析 (1)函数f(x)在[1,2]上单调递增,证明如下:任取x1,x2∈[1,2],且x1
因为x1,x2∈[1,2],且x1
所以f(x1)-f(x2)<0,即f(x1)
设t=x-,x∈[1,2],则t∈[-3,0],
设h(t)=t2-2at+8,t∈[-3,0],易知函数y=t2-2at+8的图象的对称轴为直线t=a,所以当a≤-3时,函数h(t)在[-3,0]上单调递增,
所以g(a)=h(-3)=17+6a;
当-3
故g(a)=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
