19.1 比例线段 课件1(北京课改版九年级上)
文档属性
| 名称 | 19.1 比例线段 课件1(北京课改版九年级上) |

|
|
| 格式 | rar | ||
| 文件大小 | 57.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-21 00:00:00 | ||
图片预览




文档简介
课件12张PPT。比例线段(二)练习:(1)若a、c、d、b成比例线段,则比例
式为____________,比例内项______,
比例外项_____,第四比例项______;(2)若m线段是线段a、b的比例中项,则
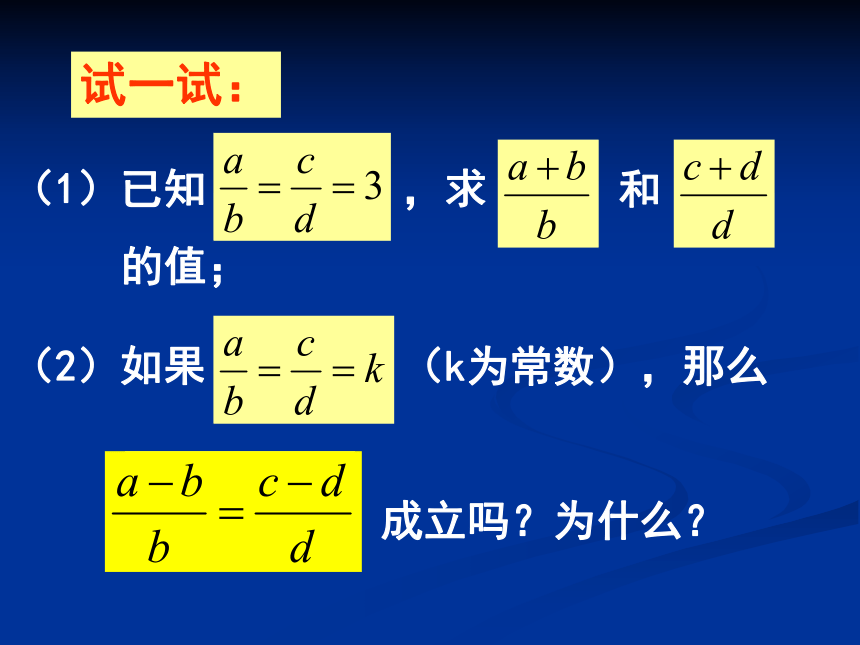
比例式为________,等积式为_______;(3)若ad=bc,则可得到多少个比例式?c、da、bbm2=ab试一试:(1)已知 ,求 和
的值;(2)如果 (k为常数),那么
成立吗?为什么?合比性质:如果 ,那么 例1.已知 ,求 , .例2.已知
求 的值.设参数法,为“桥梁”,在解题中增设k,又在解题中自行消失。当题目中出现等比的形式时通常考虑这种方法.
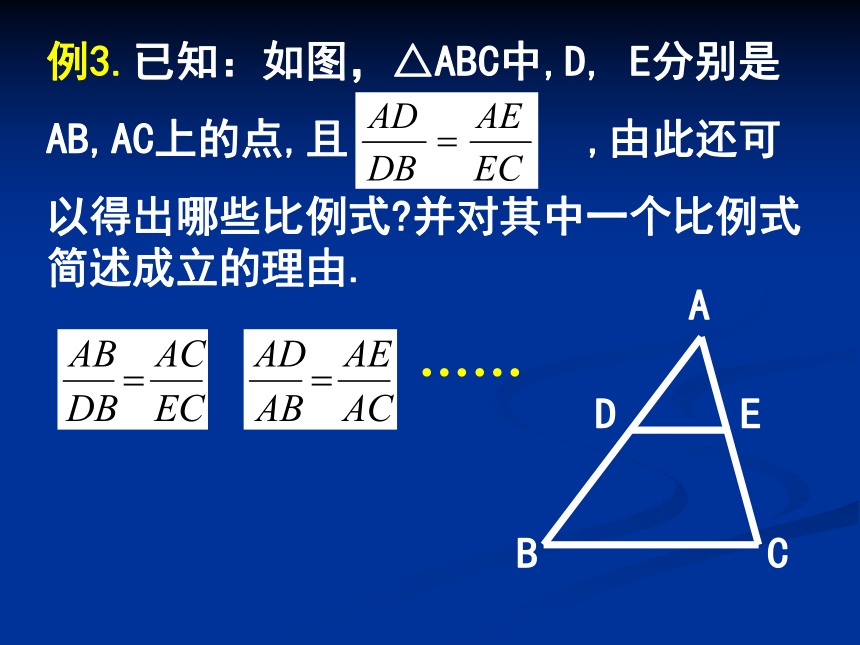
例3.已知:如图,△ABC中,D, E分别是
AB,AC上的点,且 ,由此还可
以得出哪些比例式?并对其中一个比例式简述成立的理由.……例4.已知:△ABC和△A’B’C’中, 且
,△A’B’C’的周长为50cm
求:△ABC的周长.例5:
在平面直角坐标系中,点O,A,B,C,D的坐标分别是O(0,0),A(3,4),B(3,0),C(0,-6),
D(-8,-6),则在OB,OA,AB,OC,OD,CD中,共有几组是成比例线段,请写出来.
练习⑴若m是2、3、8 的第四比例项,则m= ;⑵若线段x 是3和27的比例中项,则 x = ;⑶若 a :b :c = 2 : 3 :7 ,
又 a + b + c = 36,
则 a = ,b = ,c= . 1296921⑷已知 则 .已知 4a = 7b,你能计算出下面各式的值吗?并说明你计算的根据是什么?⑴ 比一比,看谁算得快:(2)(3)(4)小 结1、注意灵活应用比例的有关性质:基本性质: , 则 ad = bc. , 则 合比性质:设参数法2、认真观察图形,特别注意图形中线段的和、差,巧妙地与合比性质结合起来.3、要运用方程的思想来认识比例式,设出未知数,列出比例式,化为方程求解.变式练习1、同一时刻,一竿的高为1.5m,影长为1m,某塔影长20m,求塔的高.3、已知:如上图
求: 的值.
式为____________,比例内项______,
比例外项_____,第四比例项______;(2)若m线段是线段a、b的比例中项,则
比例式为________,等积式为_______;(3)若ad=bc,则可得到多少个比例式?c、da、bbm2=ab试一试:(1)已知 ,求 和
的值;(2)如果 (k为常数),那么
成立吗?为什么?合比性质:如果 ,那么 例1.已知 ,求 , .例2.已知
求 的值.设参数法,为“桥梁”,在解题中增设k,又在解题中自行消失。当题目中出现等比的形式时通常考虑这种方法.
例3.已知:如图,△ABC中,D, E分别是
AB,AC上的点,且 ,由此还可
以得出哪些比例式?并对其中一个比例式简述成立的理由.……例4.已知:△ABC和△A’B’C’中, 且
,△A’B’C’的周长为50cm
求:△ABC的周长.例5:
在平面直角坐标系中,点O,A,B,C,D的坐标分别是O(0,0),A(3,4),B(3,0),C(0,-6),
D(-8,-6),则在OB,OA,AB,OC,OD,CD中,共有几组是成比例线段,请写出来.
练习⑴若m是2、3、8 的第四比例项,则m= ;⑵若线段x 是3和27的比例中项,则 x = ;⑶若 a :b :c = 2 : 3 :7 ,
又 a + b + c = 36,
则 a = ,b = ,c= . 1296921⑷已知 则 .已知 4a = 7b,你能计算出下面各式的值吗?并说明你计算的根据是什么?⑴ 比一比,看谁算得快:(2)(3)(4)小 结1、注意灵活应用比例的有关性质:基本性质: , 则 ad = bc. , 则 合比性质:设参数法2、认真观察图形,特别注意图形中线段的和、差,巧妙地与合比性质结合起来.3、要运用方程的思想来认识比例式,设出未知数,列出比例式,化为方程求解.变式练习1、同一时刻,一竿的高为1.5m,影长为1m,某塔影长20m,求塔的高.3、已知:如上图
求: 的值.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
