19.3 平行线分三角形两边成比例 课件(北京课改版九年级上)
文档属性
| 名称 | 19.3 平行线分三角形两边成比例 课件(北京课改版九年级上) |

|
|
| 格式 | rar | ||
| 文件大小 | 65.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-21 00:00:00 | ||
图片预览

文档简介
课件20张PPT。平行线分三角形两边成比例
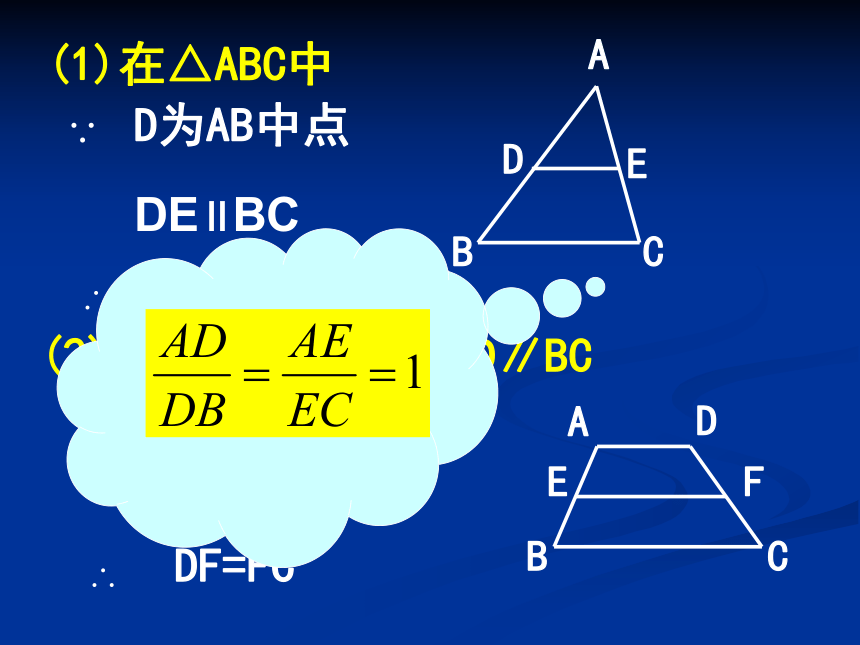
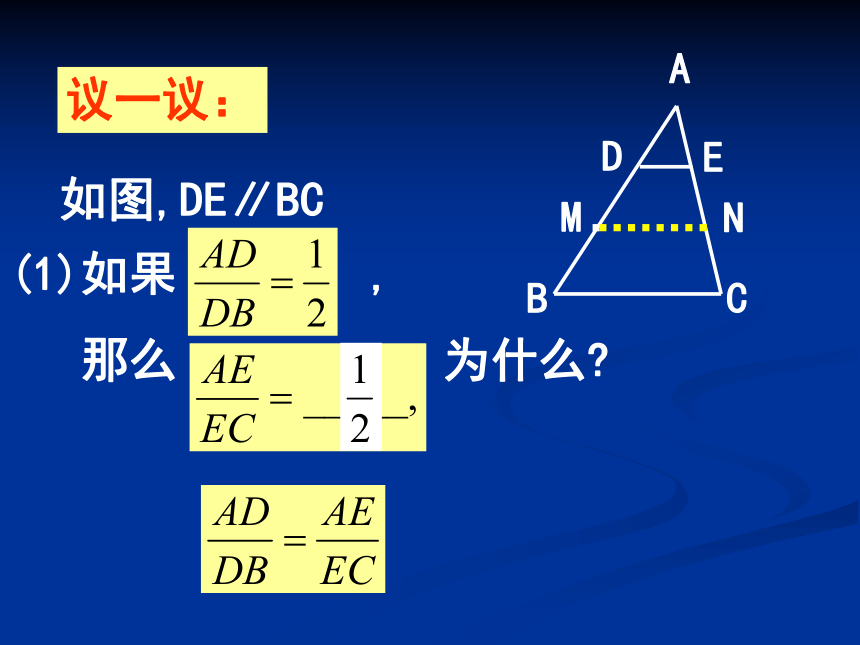
(一)(1)在△ABC中D为AB中点AE=EC(2)在梯形ABCD中, AD∥BCE为AB中点DF=FCEF∥AD∥BC议一议:如图,DE∥BC(1)如果 ,
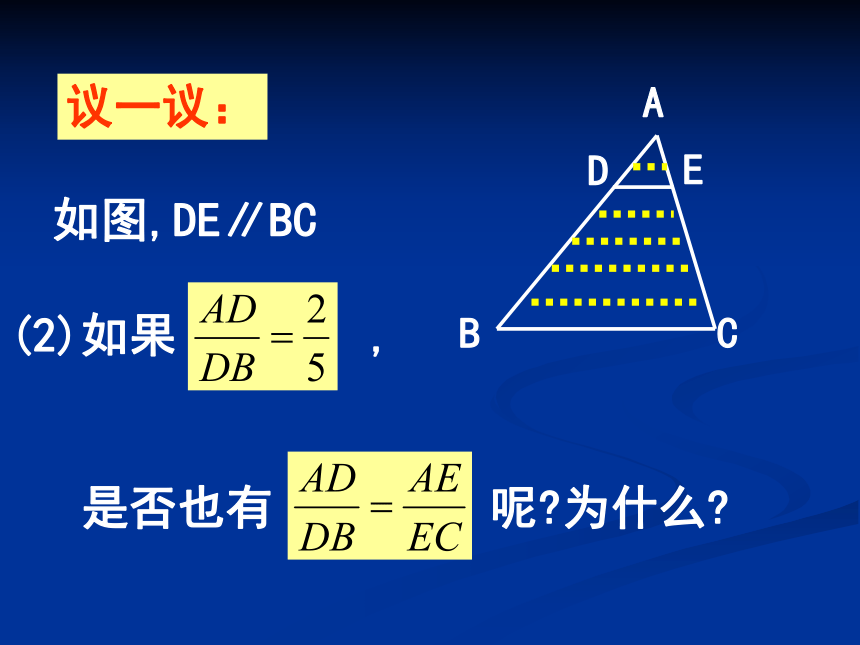
那么 为什么? N议一议:如图,DE∥BC(2)如果 ,
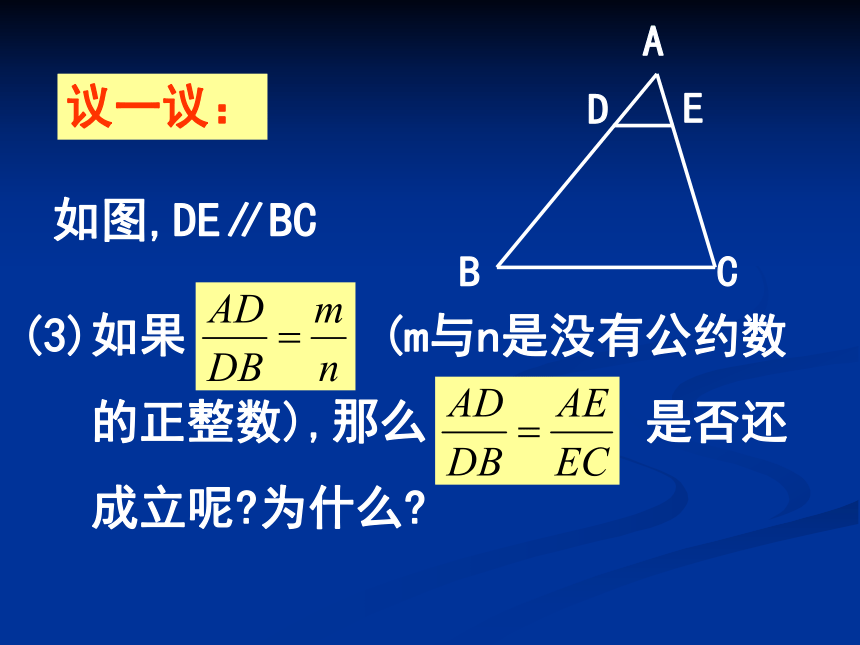
是否也有 呢?为什么? 议一议:如图,DE∥BC(3)如果 (m与n是没有公约数
的正整数),那么 是否还
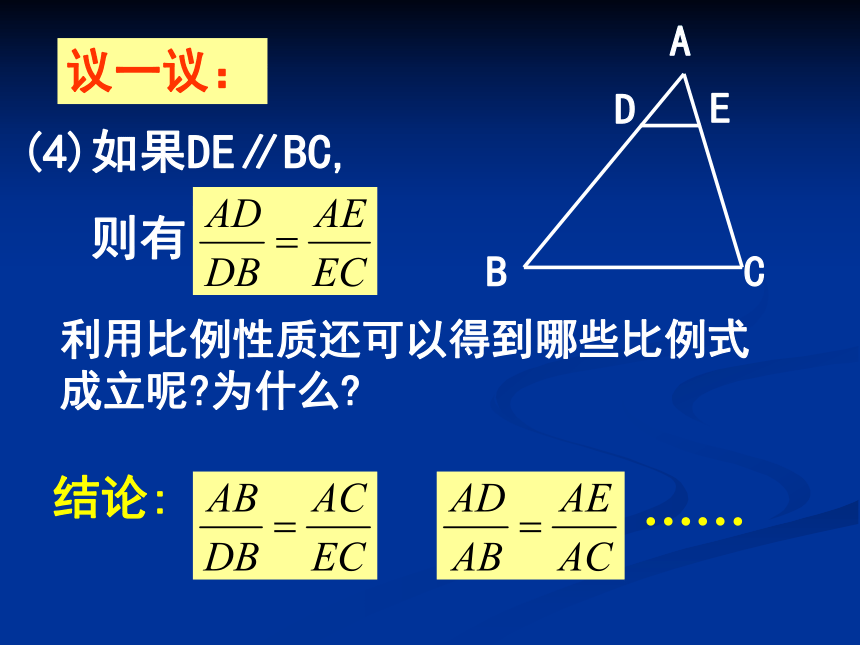
成立呢?为什么? 议一议:(4)如果DE∥BC,
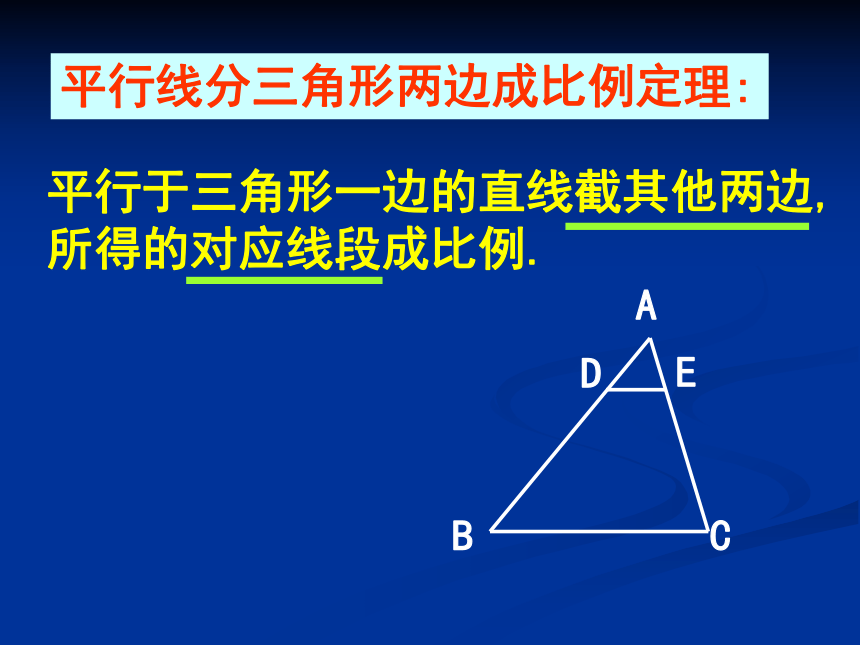
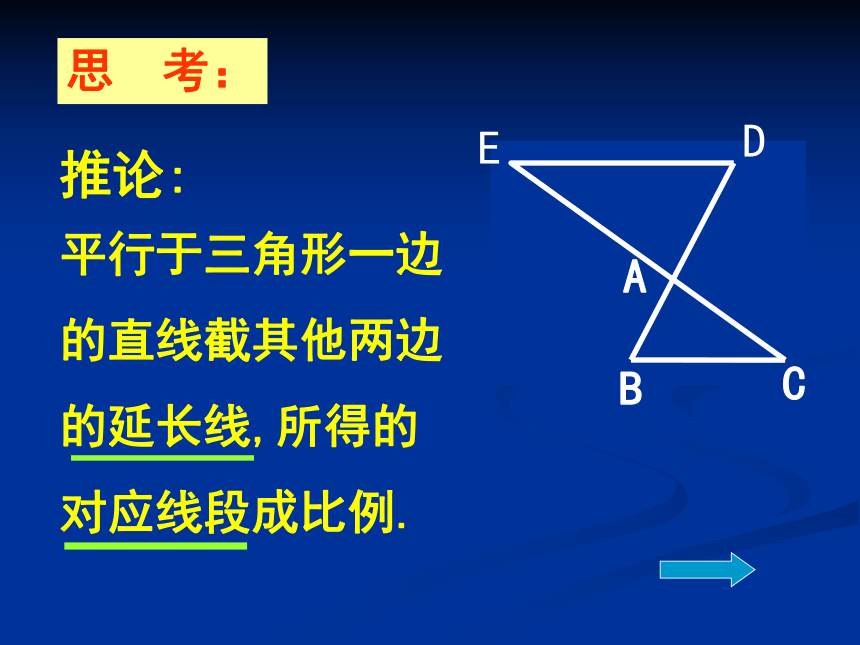
则有 结论:……利用比例性质还可以得到哪些比例式成立呢?为什么?平行线分三角形两边成比例定理:平行于三角形一边的直线截其他两边,所得的对应线段成比例.思 考:推论:平行于三角形一边
的直线截其他两边
的延长线,所得的
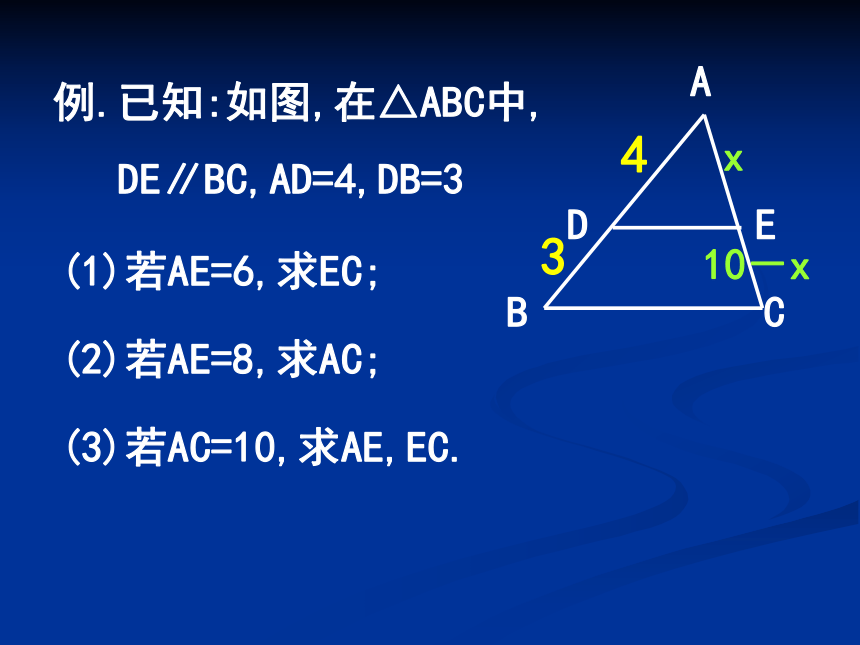
对应线段成比例.例.已知:如图,在△ABC中,
DE∥BC,AD=4,DB=3(1)若AE=6,求EC;(2)若AE=8,求AC;(3)若AC=10,求AE,EC.43x10-x课堂小结:2. 基本图形:1.平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.平行线分三角形两边成比例
(二) 基本图形:例.已知:如图,在△ABC中,
DE∥BC,EF∥AB.
试问: 成立吗?为什么?F等比代换例.已知:如图,在△ABC中,
DE∥BC,EF∥AB.
试问: 成立吗?F等线代换练习:判断下列比例式是否正确?DE∥BC,EF∥AB.(1)(2)(3)××√练习:DE∥BC,EF∥AB.若BF=2,FC=3,AB=7,
求EF的值?23?议一议:如图,AD是△ABC的中线,E是AC上任一点,BE交AD于点O,数学小组的同学在研究这一图形时,得到如下结论:(2)当 时, ;(1)当 时, ;请根据上述结论,猜想当 时(n是正整数), 的一般性结论,并说明理由.(3)当 时, ;过点D作DF∥BE交AC于点F∵ D是BC中点∴ 点F是EC中点∵∴∴∴F当 时(n是正整数),
并说明理由.课堂小结:1.分解图形:(1)等比代换:(2)等线代换:2.证比例式的常见方法:
(一)(1)在△ABC中D为AB中点AE=EC(2)在梯形ABCD中, AD∥BCE为AB中点DF=FCEF∥AD∥BC议一议:如图,DE∥BC(1)如果 ,
那么 为什么? N议一议:如图,DE∥BC(2)如果 ,
是否也有 呢?为什么? 议一议:如图,DE∥BC(3)如果 (m与n是没有公约数
的正整数),那么 是否还
成立呢?为什么? 议一议:(4)如果DE∥BC,
则有 结论:……利用比例性质还可以得到哪些比例式成立呢?为什么?平行线分三角形两边成比例定理:平行于三角形一边的直线截其他两边,所得的对应线段成比例.思 考:推论:平行于三角形一边
的直线截其他两边
的延长线,所得的
对应线段成比例.例.已知:如图,在△ABC中,
DE∥BC,AD=4,DB=3(1)若AE=6,求EC;(2)若AE=8,求AC;(3)若AC=10,求AE,EC.43x10-x课堂小结:2. 基本图形:1.平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.平行线分三角形两边成比例
(二) 基本图形:例.已知:如图,在△ABC中,
DE∥BC,EF∥AB.
试问: 成立吗?为什么?F等比代换例.已知:如图,在△ABC中,
DE∥BC,EF∥AB.
试问: 成立吗?F等线代换练习:判断下列比例式是否正确?DE∥BC,EF∥AB.(1)(2)(3)××√练习:DE∥BC,EF∥AB.若BF=2,FC=3,AB=7,
求EF的值?23?议一议:如图,AD是△ABC的中线,E是AC上任一点,BE交AD于点O,数学小组的同学在研究这一图形时,得到如下结论:(2)当 时, ;(1)当 时, ;请根据上述结论,猜想当 时(n是正整数), 的一般性结论,并说明理由.(3)当 时, ;过点D作DF∥BE交AC于点F∵ D是BC中点∴ 点F是EC中点∵∴∴∴F当 时(n是正整数),
并说明理由.课堂小结:1.分解图形:(1)等比代换:(2)等线代换:2.证比例式的常见方法:
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
