江西省南昌市第三中学2015-2016学年高一上学期入学摸底考试数学试题
文档属性
| 名称 | 江西省南昌市第三中学2015-2016学年高一上学期入学摸底考试数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 377.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-16 14:29:22 | ||
图片预览



文档简介
南昌三中2015年高一入学摸底考试
数学试卷
说明:本卷共有六个大题,21个小题,全卷满分100分,时间100分钟。
选择题(共6小题,每小题3分,共18分,每小题只有一个正确答案)
1.股票每天的涨、跌幅均不超过10%,即当涨了原价的10%后,便不能再涨,叫做涨停;当跌了原价的10%后,便不能再跌,叫做跌停。已知一支股票某天涨停,之后两天时间又跌回到原价,若这两天此股票股价的平均每天下跌的百分率为,则满足的方程是( )
A. B. C. D.
2.如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段,在连接两点所得的所有线段中任取一条线段,取到长度为的线段的概率为( )
A. B. C. D.
3.在四边形ABCD中,∠A=∠B=∠C,点E在边AB上,∠AED=60°,则一定有( )
A.∠ADE=20° B.∠ADE=30° C.∠ADE=∠ADC D.∠ADE=∠ADC
4.如图,已知正△ABC的边长为2,E、 ( http: / / www.21cnjy.com )F、G分别是AB,BC,CA上的点,且AE=BF=CG,设 △EFG的面积为y,AE的长为x,则y关于x的函数图象大致是( )
SHAPE \* MERGEFORMAT
5.已知二次函数的图象如图所示,顶点为(-1,0),下列结论:abc<0;;a>2;>0.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
6.设二次函数y1=a(x x1)(x x2)(a≠0,x1≠x2)的图象与一次函数y2=dx+e(d≠0)的图象交于点(x1,0),若函数y=y2+y1的图象与x轴仅有一个交点,则( )
A.a(x2 x1)=d B.a(x1 x2)=d
C.a(x1 x2)2=d D.a(x1+x2)2=d
填空题(共8小题,每小题3分,共24分)
7.定义运算“*”,规定x*y=a+by,其中a、b为常数,且1*2=5,2*1=6,则2*3= .
8.关于x的方程的两实数根为x1,x2,且x12+x22=3,则m= .
9.定义:给定关于x的函数y,对于该函数图 ( http: / / www.21cnjy.com )象上任意两点(x1,y1),(x2,y2),当x1﹤x2时,都有y1﹤y2,称该函数为增函数.根据以上定义,可以判断下面所给的函数中,是增函数的有 .
① y = 2x; ② y =x+1; ③ y = x2 (x>0); ④ .
10.如图,在⊙O的内接五边形ABCDE中,∠CAD=40°,则∠B+∠E= °.
11.如图,△ABC是等边三角形,高AD、BE相交于点H,BC=,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为 .
12.如图,在平面直角坐标系中,正方形OABC边长为4,M(4,m)、N(n,4)分别是AB、BC上的两个动点,且ON⊥MN,当OM最小时,= .
13.已知实数a、b、c满足a+b=ab=c,有下列结论:
①若c≠0,则;②若a=3,则b+c=9;③若a=b=c,则abc=0;④若a、b、c中只有两个数相等,则a+b+c=8.其中正确的是 .
14.若关于的方程有三个根,且这三个根恰好可
以作为一个三角形的三条边的长,则的取值范围是 .
(10题图) (11题图) (12题图)
(共2小题,每小题6分,共12分)
15.(1)先化简,再求值:,其中(满分3分)。
(2)解不等式组(满分3分)。
16.解方程。(满分6分)
(共2小题,每小题8分,共16分)
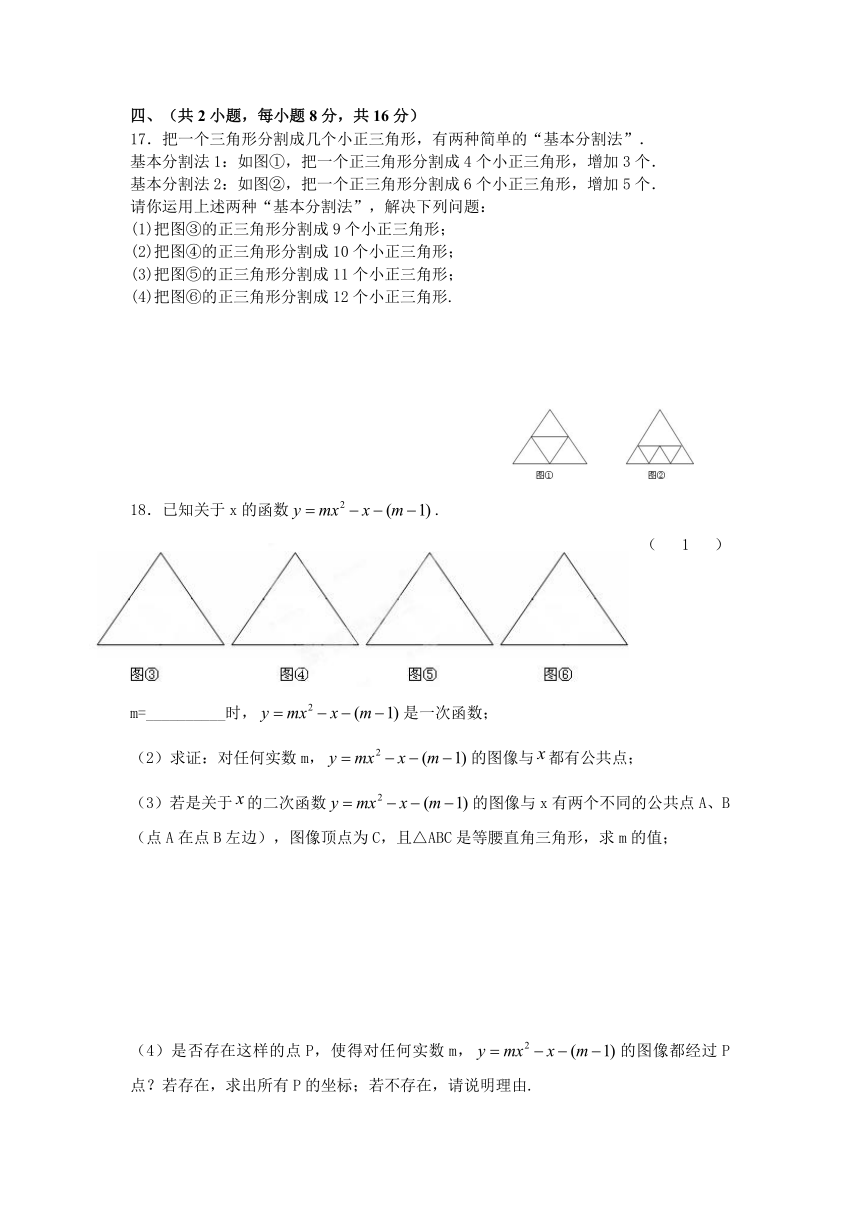
17.把一个三角形分割成几个小正三角形,有两种简单的“基本分割法”.
基本分割法1:如图①,把一个正三角形分割成4个小正三角形,增加3个.
基本分割法2:如图②,把一个正三角形分割成6个小正三角形,增加5个.
请你运用上述两种“基本分割法”,解决下列问题:
(1)把图③的正三角形分割成9个小正三角形;
(2)把图④的正三角形分割成10个小正三角形;
(3)把图⑤的正三角形分割成11个小正三角形;
(4)把图⑥的正三角形分割成12个小正三角形.
18.已知关于x的函数.
(1)m=__________时,是一次函数;
(2)求证:对任何实数m,的图像与都有公共点;
(3)若是关于的二次函数的图像与x有两个不同的公共点A、B (点A在点B左边),图像顶点为C,且△ABC是等腰直角三角形,求m的值;
(4)是否存在这样的点P,使得对任何实数m,的图像都经过P点?若存在,求出所有P的坐标;若不存在,请说明理由.
(共2小题,每小题9分,共18分)
19.如图,已知正方形ABCD,点E是BC上一点,
以AE为边作正方形AEFG。
(1)连结GD,求证△ADG≌△ABE;
(2)连结FC,求证∠FCN=45°;
(3)请问在AB边上是否存在一点Q,
使得四边形DQEF是平行四边形?
若存在,请证明;若不存在,请说明理由。
20.如图,已知抛物线经过O(0,0),A(4,0),B(3,)三点,连接AB,过点B作BC∥轴交该抛物线于点C.
(1)求这条抛物线的函数关系式.
(2)两个动点P、Q分别从O、A同时出发,以每秒1个单位长度的速度运动. 其中,点P沿着线段0A向A点运动,点Q沿着线段AB向B点运动. 设这两个动点运动的时间为(秒) (0<≤2),△PQA的面积记为S.
① 求S与的函数关系式;
② 当为何值时,S有最大值,最大值是多少?并指出此时△PQA的形状;
是否存在这样的值,使得△PQA是直角三角形 若存在,请直接写出此时P、Q两点的坐标;若不存在,请说明理由.
(本题12分)
21.在直角坐标系xOy中,已知点P是反比例函数y=(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
(1)如图1,⊙P运动到与x轴相切,设切点为K,判断四边形OKPA的形状,并说明理由.
(2)如图2,⊙P运动到与x轴相交,设交点为B,C.当四边形ABCP是菱形时:
①求出点A,B,C的坐标.
②在过A,B,C三点的抛物线上是否存在点M,使△MBP的面积是菱形ABCP面积的?若存在,试求出所有满足条件的M点的坐标;若不存在,试说明理由.
南昌三中2015年高一入学摸底考试
数学答卷
一、选择题(共6小题,每小题3分,共18分,每小题只有一个正确选项)
题号 1 2 3 4 5 6
答案
二、填空题(共8小题,每小题3分,共24分)
7. 8. 9. 10.
11. 12. 13. 14.
(共2小题,每小题6分,共12分)
15.(1)
(2)
16.
(共2小题,每小题8分,共16分)
17.
18.
(共2小题,每小题9分,共18分)
19.
20.
六、(本题12分)
21.
高一数学参考答案
一、选择题(共6小题,每小题3分,共18分,每小题只有一个正确选项)
题号 1 2 3 4 5 6
答案 D B C D B A
二、填空题(共8小题,每小题3分,共24分)
7. 10 8. 0 9. ①③ 10. 220
11. 12. 5 13. ①③④ 14.
(共2小题,每小题6分,共12分)
15.(1)原式==
当=-5时,原式=3。
(2)由①得:
由②得:
原不等式组的解集为。
当时,原方程可化为
,
当时,原方程可化为
,
原方程的解为或
(共2小题,每小题8分,共16分)
17.(1)如图③的正三角形分割成9个小正三角形;
(2)如图④的正三角形分割成10个小正三角形;
(3)如图⑤的正三角形分割成11个小正三角形;
(4)如图⑥的正三角形分割成12个小正三角形.
( http: / / www.21cnjy.com )
18.(1)根据题意得:m=0
(2)m=0 时,y=-x+1与x轴交于点(1,0)
m≠0时,△=+4m(m-1)=≥0
∴对任何实数m,y=m-x-(m-1)的图像与x都有公共点;
(3) 由m-x-(m-1)=0得=1,∴AB=
且顶点C的纵坐标
∵△ABC是等腰直角三角形
∴AB=2即
∴m=或m=,或m=-
经检验m=,或m=-
(4)由m=0得y=-x+1, m=1得y=-x
由 解得或对任何实数m
当x=1时,y=m-x-(m-1)=m-1-(m-1)=0
当x=-1时,y=m-x-(m-1)=m+1-(m-1)=2
对任何实数m,y=m-x-(m-1)的图像都经过点(1,0)(-1,2)
即所求点P的坐标为(1,0)或(-1,2)
(共2小题,每小题9分,共18分)
19.(1)如图,连接DG
∵四边形ABCD和四边形AEFG是正方形
∴DA=BA,EA=GA,∠BAD=∠EAG=90°
∴∠DAG=∠BAE
∴△ADG≌△ABE;
(2)过F作BN的垂线,设垂足为H
∵∠BAE+∠AEB=90°,∠FEH+∠AEB=90°
∴∠BAE=∠HEF
∵AE=EF
∴△ABE≌△EHF
∴AB=EH,BE=FH
∴AB=BC=EH
∴BE+EC=EC+CH
∴CH=BE=FH
∴∠FCN=45°;
(3)在AB上取AQ=BE,连接QD
∵AB=AD
∴△DAQ≌△ABE
∵△ABE≌△EHF
∴△DAQ≌△ABE≌△ADG
∴∠GAD=∠ADQ
∴AG、QD平行且相等
又∵AG、EF平行且相等
∴QD、EF平行且相等
∴四边形DQEF是平行四边形
∴在AB边上存在一点Q,使得四边形DQEF
是平行四边形.
20.(1)
(2)①过B作
由题意QA=t, PA=4—t
过点Q作轴交x轴于F,则
②
此时
存在,当点Q在AB上运动时,要使得是直角,必须使.
∴PA=2QA
∴4—t=2t.
(本题12分)
21.(1)四边形OKPA是正方形.
证明:∵⊙P分别与两坐标轴相切,
∴PA⊥OA,PK⊥OK.
∴∠PAO=∠OKP=90°.
又∵∠AOK=90°,
∴∠PAO=∠OKP=∠AOK=90°.
∴四边形OKPA是矩形.
又∵AP=KP,
∴四边形OKPA是正方形.
(2)①连接PB.过点P作PG⊥BC于G.
∵四边形ABCP为菱形,
∴BC=PA=PB=PC(半径).
∴△PBC为等边三角形.在Rt△PBG中,∠PBG=60°,PB=PA=x,PG=
∴P()带入
解之得:x=±2(负值舍去).
∴PG=,PA=BC=2.P(2, )
易知四边形OGPA是矩形,PA=OG=2,BG=CG=1,
∴OB=OG-BG=1,OC=OG+GC=3.
∴A(0,),B(1,0),C(3,0).
②设二次函数解析式为:,过点A(0,),
∴ ∴二次函数解析式为:y=x2 x+
设直线BP的解析式为:y=ux+v,据题意得:解之得:.
∴直线BP的解析式为:y= x-,
要使
过点A作直线AM∥BP,则可得直线AM的解析式为:y=x+.
解方程组:
得:;.
过点C作直线CM∥PB,则可设直线CM的解析式为:y=x+t.
∴0=3+t.
∴t= 3.
∴直线CM的解析式为:y=x 3.
解方程组:
得:;..
综上可知,满足条件的M的坐标有四个,
分别为:(0,),(3,0),(4,),(7,8)
A
B
C
D
E
F
G
N
姓名
班级
学号
数学试卷
说明:本卷共有六个大题,21个小题,全卷满分100分,时间100分钟。
选择题(共6小题,每小题3分,共18分,每小题只有一个正确答案)
1.股票每天的涨、跌幅均不超过10%,即当涨了原价的10%后,便不能再涨,叫做涨停;当跌了原价的10%后,便不能再跌,叫做跌停。已知一支股票某天涨停,之后两天时间又跌回到原价,若这两天此股票股价的平均每天下跌的百分率为,则满足的方程是( )
A. B. C. D.
2.如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段,在连接两点所得的所有线段中任取一条线段,取到长度为的线段的概率为( )
A. B. C. D.
3.在四边形ABCD中,∠A=∠B=∠C,点E在边AB上,∠AED=60°,则一定有( )
A.∠ADE=20° B.∠ADE=30° C.∠ADE=∠ADC D.∠ADE=∠ADC
4.如图,已知正△ABC的边长为2,E、 ( http: / / www.21cnjy.com )F、G分别是AB,BC,CA上的点,且AE=BF=CG,设 △EFG的面积为y,AE的长为x,则y关于x的函数图象大致是( )
SHAPE \* MERGEFORMAT
5.已知二次函数的图象如图所示,顶点为(-1,0),下列结论:abc<0;;a>2;>0.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
6.设二次函数y1=a(x x1)(x x2)(a≠0,x1≠x2)的图象与一次函数y2=dx+e(d≠0)的图象交于点(x1,0),若函数y=y2+y1的图象与x轴仅有一个交点,则( )
A.a(x2 x1)=d B.a(x1 x2)=d
C.a(x1 x2)2=d D.a(x1+x2)2=d
填空题(共8小题,每小题3分,共24分)
7.定义运算“*”,规定x*y=a+by,其中a、b为常数,且1*2=5,2*1=6,则2*3= .
8.关于x的方程的两实数根为x1,x2,且x12+x22=3,则m= .
9.定义:给定关于x的函数y,对于该函数图 ( http: / / www.21cnjy.com )象上任意两点(x1,y1),(x2,y2),当x1﹤x2时,都有y1﹤y2,称该函数为增函数.根据以上定义,可以判断下面所给的函数中,是增函数的有 .
① y = 2x; ② y =x+1; ③ y = x2 (x>0); ④ .
10.如图,在⊙O的内接五边形ABCDE中,∠CAD=40°,则∠B+∠E= °.
11.如图,△ABC是等边三角形,高AD、BE相交于点H,BC=,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为 .
12.如图,在平面直角坐标系中,正方形OABC边长为4,M(4,m)、N(n,4)分别是AB、BC上的两个动点,且ON⊥MN,当OM最小时,= .
13.已知实数a、b、c满足a+b=ab=c,有下列结论:
①若c≠0,则;②若a=3,则b+c=9;③若a=b=c,则abc=0;④若a、b、c中只有两个数相等,则a+b+c=8.其中正确的是 .
14.若关于的方程有三个根,且这三个根恰好可
以作为一个三角形的三条边的长,则的取值范围是 .
(10题图) (11题图) (12题图)
(共2小题,每小题6分,共12分)
15.(1)先化简,再求值:,其中(满分3分)。
(2)解不等式组(满分3分)。
16.解方程。(满分6分)
(共2小题,每小题8分,共16分)
17.把一个三角形分割成几个小正三角形,有两种简单的“基本分割法”.
基本分割法1:如图①,把一个正三角形分割成4个小正三角形,增加3个.
基本分割法2:如图②,把一个正三角形分割成6个小正三角形,增加5个.
请你运用上述两种“基本分割法”,解决下列问题:
(1)把图③的正三角形分割成9个小正三角形;
(2)把图④的正三角形分割成10个小正三角形;
(3)把图⑤的正三角形分割成11个小正三角形;
(4)把图⑥的正三角形分割成12个小正三角形.
18.已知关于x的函数.
(1)m=__________时,是一次函数;
(2)求证:对任何实数m,的图像与都有公共点;
(3)若是关于的二次函数的图像与x有两个不同的公共点A、B (点A在点B左边),图像顶点为C,且△ABC是等腰直角三角形,求m的值;
(4)是否存在这样的点P,使得对任何实数m,的图像都经过P点?若存在,求出所有P的坐标;若不存在,请说明理由.
(共2小题,每小题9分,共18分)
19.如图,已知正方形ABCD,点E是BC上一点,
以AE为边作正方形AEFG。
(1)连结GD,求证△ADG≌△ABE;
(2)连结FC,求证∠FCN=45°;
(3)请问在AB边上是否存在一点Q,
使得四边形DQEF是平行四边形?
若存在,请证明;若不存在,请说明理由。
20.如图,已知抛物线经过O(0,0),A(4,0),B(3,)三点,连接AB,过点B作BC∥轴交该抛物线于点C.
(1)求这条抛物线的函数关系式.
(2)两个动点P、Q分别从O、A同时出发,以每秒1个单位长度的速度运动. 其中,点P沿着线段0A向A点运动,点Q沿着线段AB向B点运动. 设这两个动点运动的时间为(秒) (0<≤2),△PQA的面积记为S.
① 求S与的函数关系式;
② 当为何值时,S有最大值,最大值是多少?并指出此时△PQA的形状;
是否存在这样的值,使得△PQA是直角三角形 若存在,请直接写出此时P、Q两点的坐标;若不存在,请说明理由.
(本题12分)
21.在直角坐标系xOy中,已知点P是反比例函数y=(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
(1)如图1,⊙P运动到与x轴相切,设切点为K,判断四边形OKPA的形状,并说明理由.
(2)如图2,⊙P运动到与x轴相交,设交点为B,C.当四边形ABCP是菱形时:
①求出点A,B,C的坐标.
②在过A,B,C三点的抛物线上是否存在点M,使△MBP的面积是菱形ABCP面积的?若存在,试求出所有满足条件的M点的坐标;若不存在,试说明理由.
南昌三中2015年高一入学摸底考试
数学答卷
一、选择题(共6小题,每小题3分,共18分,每小题只有一个正确选项)
题号 1 2 3 4 5 6
答案
二、填空题(共8小题,每小题3分,共24分)
7. 8. 9. 10.
11. 12. 13. 14.
(共2小题,每小题6分,共12分)
15.(1)
(2)
16.
(共2小题,每小题8分,共16分)
17.
18.
(共2小题,每小题9分,共18分)
19.
20.
六、(本题12分)
21.
高一数学参考答案
一、选择题(共6小题,每小题3分,共18分,每小题只有一个正确选项)
题号 1 2 3 4 5 6
答案 D B C D B A
二、填空题(共8小题,每小题3分,共24分)
7. 10 8. 0 9. ①③ 10. 220
11. 12. 5 13. ①③④ 14.
(共2小题,每小题6分,共12分)
15.(1)原式==
当=-5时,原式=3。
(2)由①得:
由②得:
原不等式组的解集为。
当时,原方程可化为
,
当时,原方程可化为
,
原方程的解为或
(共2小题,每小题8分,共16分)
17.(1)如图③的正三角形分割成9个小正三角形;
(2)如图④的正三角形分割成10个小正三角形;
(3)如图⑤的正三角形分割成11个小正三角形;
(4)如图⑥的正三角形分割成12个小正三角形.
( http: / / www.21cnjy.com )
18.(1)根据题意得:m=0
(2)m=0 时,y=-x+1与x轴交于点(1,0)
m≠0时,△=+4m(m-1)=≥0
∴对任何实数m,y=m-x-(m-1)的图像与x都有公共点;
(3) 由m-x-(m-1)=0得=1,∴AB=
且顶点C的纵坐标
∵△ABC是等腰直角三角形
∴AB=2即
∴m=或m=,或m=-
经检验m=,或m=-
(4)由m=0得y=-x+1, m=1得y=-x
由 解得或对任何实数m
当x=1时,y=m-x-(m-1)=m-1-(m-1)=0
当x=-1时,y=m-x-(m-1)=m+1-(m-1)=2
对任何实数m,y=m-x-(m-1)的图像都经过点(1,0)(-1,2)
即所求点P的坐标为(1,0)或(-1,2)
(共2小题,每小题9分,共18分)
19.(1)如图,连接DG
∵四边形ABCD和四边形AEFG是正方形
∴DA=BA,EA=GA,∠BAD=∠EAG=90°
∴∠DAG=∠BAE
∴△ADG≌△ABE;
(2)过F作BN的垂线,设垂足为H
∵∠BAE+∠AEB=90°,∠FEH+∠AEB=90°
∴∠BAE=∠HEF
∵AE=EF
∴△ABE≌△EHF
∴AB=EH,BE=FH
∴AB=BC=EH
∴BE+EC=EC+CH
∴CH=BE=FH
∴∠FCN=45°;
(3)在AB上取AQ=BE,连接QD
∵AB=AD
∴△DAQ≌△ABE
∵△ABE≌△EHF
∴△DAQ≌△ABE≌△ADG
∴∠GAD=∠ADQ
∴AG、QD平行且相等
又∵AG、EF平行且相等
∴QD、EF平行且相等
∴四边形DQEF是平行四边形
∴在AB边上存在一点Q,使得四边形DQEF
是平行四边形.
20.(1)
(2)①过B作
由题意QA=t, PA=4—t
过点Q作轴交x轴于F,则
②
此时
存在,当点Q在AB上运动时,要使得是直角,必须使.
∴PA=2QA
∴4—t=2t.
(本题12分)
21.(1)四边形OKPA是正方形.
证明:∵⊙P分别与两坐标轴相切,
∴PA⊥OA,PK⊥OK.
∴∠PAO=∠OKP=90°.
又∵∠AOK=90°,
∴∠PAO=∠OKP=∠AOK=90°.
∴四边形OKPA是矩形.
又∵AP=KP,
∴四边形OKPA是正方形.
(2)①连接PB.过点P作PG⊥BC于G.
∵四边形ABCP为菱形,
∴BC=PA=PB=PC(半径).
∴△PBC为等边三角形.在Rt△PBG中,∠PBG=60°,PB=PA=x,PG=
∴P()带入
解之得:x=±2(负值舍去).
∴PG=,PA=BC=2.P(2, )
易知四边形OGPA是矩形,PA=OG=2,BG=CG=1,
∴OB=OG-BG=1,OC=OG+GC=3.
∴A(0,),B(1,0),C(3,0).
②设二次函数解析式为:,过点A(0,),
∴ ∴二次函数解析式为:y=x2 x+
设直线BP的解析式为:y=ux+v,据题意得:解之得:.
∴直线BP的解析式为:y= x-,
要使
过点A作直线AM∥BP,则可得直线AM的解析式为:y=x+.
解方程组:
得:;.
过点C作直线CM∥PB,则可设直线CM的解析式为:y=x+t.
∴0=3+t.
∴t= 3.
∴直线CM的解析式为:y=x 3.
解方程组:
得:;..
综上可知,满足条件的M的坐标有四个,
分别为:(0,),(3,0),(4,),(7,8)
A
B
C
D
E
F
G
N
姓名
班级
学号
同课章节目录
