19.6 相似三角形的性质 课件1(北京课改版九年级上)
文档属性
| 名称 | 19.6 相似三角形的性质 课件1(北京课改版九年级上) |

|
|
| 格式 | rar | ||
| 文件大小 | 155.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-21 00:00:00 | ||
图片预览



文档简介
课件19张PPT。 相似三角形的性质相似三角形的性质
1 相似三角形的对应角相等,对应边成比例.
2 相似三角形对应高的比,对应中线的比与
对应角平分线的比都等于相似比.
3 相似三角形周长的比等于相似比,
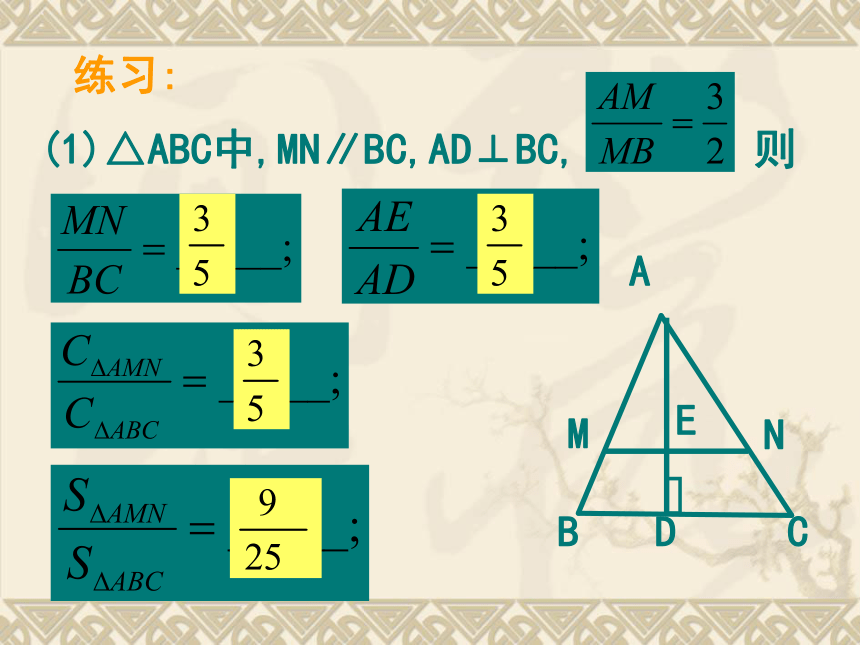
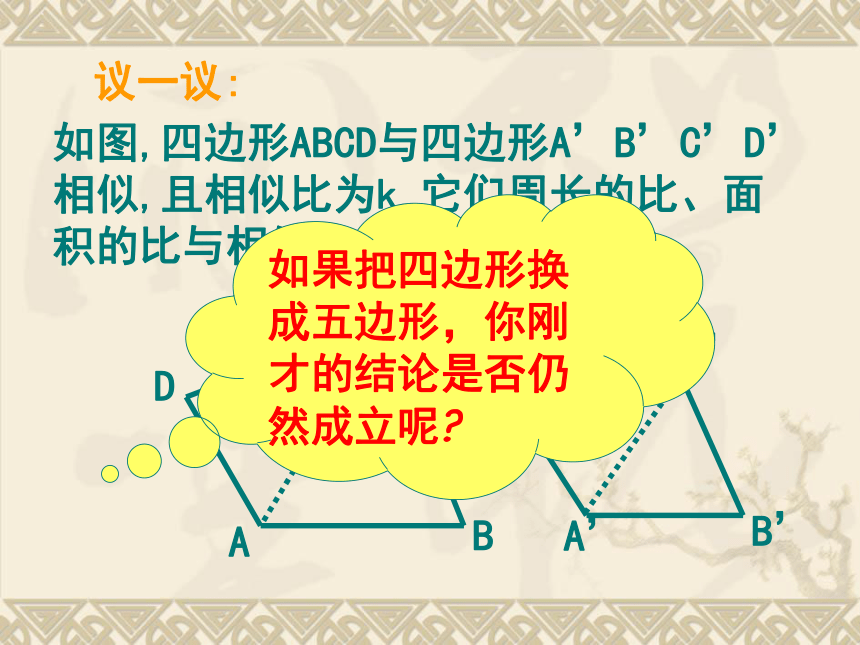
面积比等于相似比的平方.复习练习:△ABC中,MN∥BC,AD⊥BC, 则MNE议一议:如图,四边形ABCD与四边形A’B’C’D’相似,且相似比为k,它们周长的比、面积的比与相似比有什么关系?如果把四边形换成五边形,你刚才的结论是否仍然成立呢?
相似多边形的周长比等于 ,
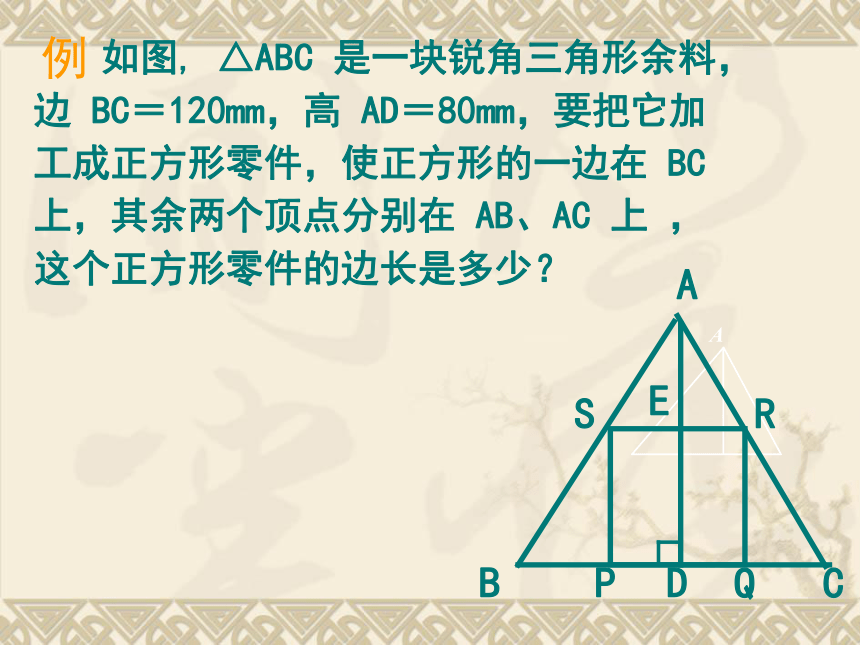
面积比等于 _________. 相似比相似比的平方相似多边形的性质: 如图, △ABC 是一块锐角三角形余料,边 BC=120mm,高 AD=80mm,要把它加工成正方形零件,使正方形的一边在 BC上,其余两个顶点分别在 AB、AC 上 ,这个正方形零件的边长是多少?
例A 如图,△ABC的高AD与边SR相交于点E . 设正方形的边长为x mm .
∵SR∥BC,
∴ △ASR∽△ABC.
∴
解得 x =48(mm).
答:加工成的正方形零件的边长为48mm.解:(相似三角形的对应
高的比等于相似比).(相似三角形判定的
预备定理). 已知:△ABC 中,∠A=90 °,四边
形DEFG为正方形,G、F分别在AB、AC
上,D、E在BC上.
1、图中有多少个直角三角形?
2、这些直角三角形中哪些三角形是相似的?
答:
1、有4个,他们是
△BAC,△BDG,
△FEC,△GAF
2、△BAC,△BDG, △FEC,
△GAF彼此都是相似三角形.变式1
小 结相似多边形的性质:
相似三角形对应高的比,周长的比都等于相似比.
相似三角形面积的比等于相似比的平方.
相似多边形周长的比等于相似比.
相似多边形面积的比等于相似比的平方. 自我测试
1、两个矩形相似,它们的对角线之比是1:3,那么
它们的相似比是___,周长比是____,面积比是____
2、若两个相似三角形的相似比是3:5,其中第一
个三角形的周长为21cm,则第二个三角形的
周长为 cm.
3、如果把一个三角形每条边的长都扩大为原来
的5倍,那么它的周长扩大为原来的 倍,
而面积扩大为原来的 倍。
4、如图,已知△ABC∽△ADE,
且BC=2DE,则△ADE与四
边形BCDE的面积比为( )
(A)1:2 (B)1:3 (C)1;4 (D)1:5 1:31:31:935525B AD是Rt △ABC斜边上的高.
1)已知BD=9cm, AD=6cm,求DC;
2)已知BC=25cm, AC=15cm,求DC.变式2解1) ∵ △ABC是直角三角形
AD是斜边BC上的高,
∴ △BAD∽△ACD.
∴
即 ∴ 如图5,PD⊥BC于D, BA⊥PC于
A, 则图中相似三角形共有_____对.
分析:易证△BAC、△BDG、 △PAG、
△PDC彼此都是相似三角形.
变式3图56分离基本图形 如图6,△BAC中,∠BAC=90 °
GD⊥BC于D, AD交GC于E .
求证:1)∠BAD =∠BCG. 2)△DEG∽△CEA .
证明:1) ∵∠BDG=∠A=90°,∠B= ∠ B ,
∴ △BAC∽△BDG .
∴
∴
∴ △BAD∽△BCG .
∴ ∠BAD = ∠BCG.变式4 证明: 2) 由1) ∠BCG =∠BAD,
∵∠DEC =∠GEA,
∴△DEC ∽△GEA,
∴ ,
∴ .
∵∠DEG =∠CEA,
∴△DEG∽△CEA . 如图7, △BAC中,AB=AC,BD⊥AC
于D.
求证: .
分析:如何处理结论中的2
是解答此题的关键. 根据
考虑作一条线段等于2CD
或 BC 或2CA, 再证明两个三角形相似.练习 例.判断正误:
1)如果把一个三角形三边的长同时扩大为原来的
10倍,那么它的周长也扩大为原来的10倍。
2)如果把一个三角形的面积扩大为原来的9倍,
那么它的三边也都扩大为原来的9倍。 例.如图所示,D、E分别是AC、AB上的点, 已知△ABC的面积为100cm2 , 求四边形BCDE的面积.解:∵,∠A=∠A∴∽△△(两边对应成比例,且夹角相等,两三角形相似)∴(相似三角形面积的比等于
相似比的平方)(以下解略)22ACAESSABCADE=DDABCADE归纳提炼相似多边形的性质:
相似三角形对应高的比,对应角平分线的比,对应中线的比,对应周长的比都等于相似比.
相似三角形面积的比等于相似比的平方.
相似多边形对应对角线的比等于相似比.
相似多边形对应三角形相似,且相似比等于相似多边形的相似比.
相似多边形对应三角形面积的比等于相似多边形的相似比的平方.
相似多边形面积的比等于相似比的平方.小 结性质定理: 2.相似三角形周长的比等于相似比,
面积的比等于相似比的平方1. 相似三角形对应高的比等于相似比
相似三角形对应角分线的比与相似比有什么关系?
相似三角形对应中线的比和相似比有什么关系?
1 相似三角形的对应角相等,对应边成比例.
2 相似三角形对应高的比,对应中线的比与
对应角平分线的比都等于相似比.
3 相似三角形周长的比等于相似比,
面积比等于相似比的平方.复习练习:△ABC中,MN∥BC,AD⊥BC, 则MNE议一议:如图,四边形ABCD与四边形A’B’C’D’相似,且相似比为k,它们周长的比、面积的比与相似比有什么关系?如果把四边形换成五边形,你刚才的结论是否仍然成立呢?
相似多边形的周长比等于 ,
面积比等于 _________. 相似比相似比的平方相似多边形的性质: 如图, △ABC 是一块锐角三角形余料,边 BC=120mm,高 AD=80mm,要把它加工成正方形零件,使正方形的一边在 BC上,其余两个顶点分别在 AB、AC 上 ,这个正方形零件的边长是多少?
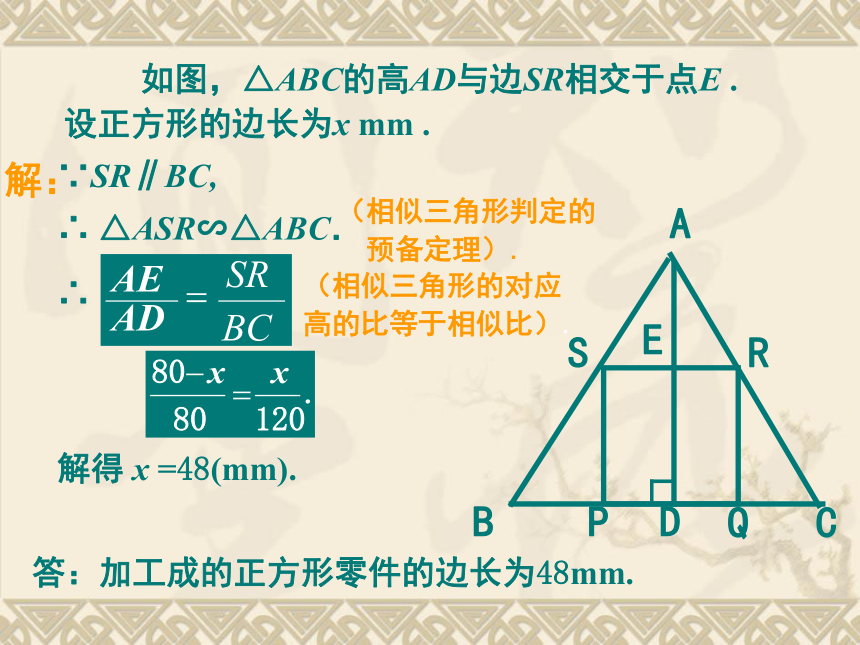
例A 如图,△ABC的高AD与边SR相交于点E . 设正方形的边长为x mm .
∵SR∥BC,
∴ △ASR∽△ABC.
∴
解得 x =48(mm).
答:加工成的正方形零件的边长为48mm.解:(相似三角形的对应
高的比等于相似比).(相似三角形判定的
预备定理). 已知:△ABC 中,∠A=90 °,四边
形DEFG为正方形,G、F分别在AB、AC
上,D、E在BC上.
1、图中有多少个直角三角形?
2、这些直角三角形中哪些三角形是相似的?
答:
1、有4个,他们是
△BAC,△BDG,
△FEC,△GAF
2、△BAC,△BDG, △FEC,
△GAF彼此都是相似三角形.变式1
小 结相似多边形的性质:
相似三角形对应高的比,周长的比都等于相似比.
相似三角形面积的比等于相似比的平方.
相似多边形周长的比等于相似比.
相似多边形面积的比等于相似比的平方. 自我测试
1、两个矩形相似,它们的对角线之比是1:3,那么
它们的相似比是___,周长比是____,面积比是____
2、若两个相似三角形的相似比是3:5,其中第一
个三角形的周长为21cm,则第二个三角形的
周长为 cm.
3、如果把一个三角形每条边的长都扩大为原来
的5倍,那么它的周长扩大为原来的 倍,
而面积扩大为原来的 倍。
4、如图,已知△ABC∽△ADE,
且BC=2DE,则△ADE与四
边形BCDE的面积比为( )
(A)1:2 (B)1:3 (C)1;4 (D)1:5 1:31:31:935525B AD是Rt △ABC斜边上的高.
1)已知BD=9cm, AD=6cm,求DC;
2)已知BC=25cm, AC=15cm,求DC.变式2解1) ∵ △ABC是直角三角形
AD是斜边BC上的高,
∴ △BAD∽△ACD.
∴
即 ∴ 如图5,PD⊥BC于D, BA⊥PC于
A, 则图中相似三角形共有_____对.
分析:易证△BAC、△BDG、 △PAG、
△PDC彼此都是相似三角形.
变式3图56分离基本图形 如图6,△BAC中,∠BAC=90 °
GD⊥BC于D, AD交GC于E .
求证:1)∠BAD =∠BCG. 2)△DEG∽△CEA .
证明:1) ∵∠BDG=∠A=90°,∠B= ∠ B ,
∴ △BAC∽△BDG .
∴
∴
∴ △BAD∽△BCG .
∴ ∠BAD = ∠BCG.变式4 证明: 2) 由1) ∠BCG =∠BAD,
∵∠DEC =∠GEA,
∴△DEC ∽△GEA,
∴ ,
∴ .
∵∠DEG =∠CEA,
∴△DEG∽△CEA . 如图7, △BAC中,AB=AC,BD⊥AC
于D.
求证: .
分析:如何处理结论中的2
是解答此题的关键. 根据
考虑作一条线段等于2CD
或 BC 或2CA, 再证明两个三角形相似.练习 例.判断正误:
1)如果把一个三角形三边的长同时扩大为原来的
10倍,那么它的周长也扩大为原来的10倍。
2)如果把一个三角形的面积扩大为原来的9倍,
那么它的三边也都扩大为原来的9倍。 例.如图所示,D、E分别是AC、AB上的点, 已知△ABC的面积为100cm2 , 求四边形BCDE的面积.解:∵,∠A=∠A∴∽△△(两边对应成比例,且夹角相等,两三角形相似)∴(相似三角形面积的比等于
相似比的平方)(以下解略)22ACAESSABCADE=DDABCADE归纳提炼相似多边形的性质:
相似三角形对应高的比,对应角平分线的比,对应中线的比,对应周长的比都等于相似比.
相似三角形面积的比等于相似比的平方.
相似多边形对应对角线的比等于相似比.
相似多边形对应三角形相似,且相似比等于相似多边形的相似比.
相似多边形对应三角形面积的比等于相似多边形的相似比的平方.
相似多边形面积的比等于相似比的平方.小 结性质定理: 2.相似三角形周长的比等于相似比,
面积的比等于相似比的平方1. 相似三角形对应高的比等于相似比
相似三角形对应角分线的比与相似比有什么关系?
相似三角形对应中线的比和相似比有什么关系?
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
