沪科版九年级数学上册试题 第22章《相似形》章节测试卷(含答案)
文档属性
| 名称 | 沪科版九年级数学上册试题 第22章《相似形》章节测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 778.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-19 09:42:11 | ||
图片预览



文档简介
第22章《相似形》章节测试卷
一.选择题(共10小题,满分30分,每小题3分)
1.已知,则直线一定经过( )
A.第一、二象限 B.第二、三家限
C.第三、四象限 D.第一、四象限
2.如图,已知,添加下列条件后,仍无法判定的是( )
A. B. C. D.
3.如图,在中,点在的延长线上,分别交、于点、,则图中相似三角形共有( )
A.4对 B.5对 C.6对 D.7对
4.如图,在中,点在边上,连接,交于点.则下列结论正确的是( ).
A. B. C. D.
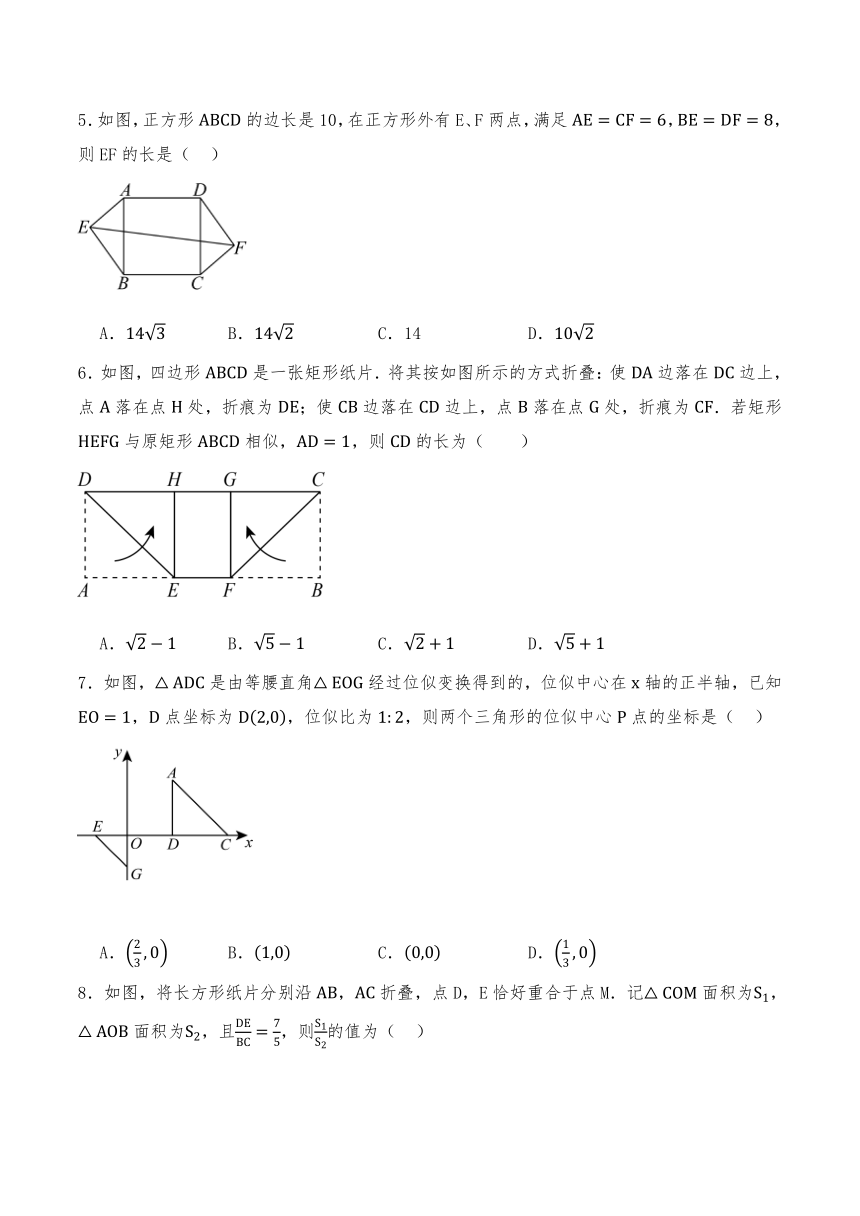
5.如图,正方形的边长是10,在正方形外有E、F两点,满足,,则EF的长是( )
A. B. C.14 D.
6.如图,四边形是一张矩形纸片.将其按如图所示的方式折叠:使边落在边上,点落在点处,折痕为;使边落在边上,点落在点处,折痕为.若矩形与原矩形相似,,则的长为( )
A. B. C. D.
7.如图,是由等腰直角经过位似变换得到的,位似中心在轴的正半轴,已知,点坐标为,位似比为,则两个三角形的位似中心点的坐标是( )
A. B. C. D.
8.如图,将长方形纸片分别沿,折叠,点D,E恰好重合于点M.记面积为,面积为,且,则的值为( )
A. B. C. D.
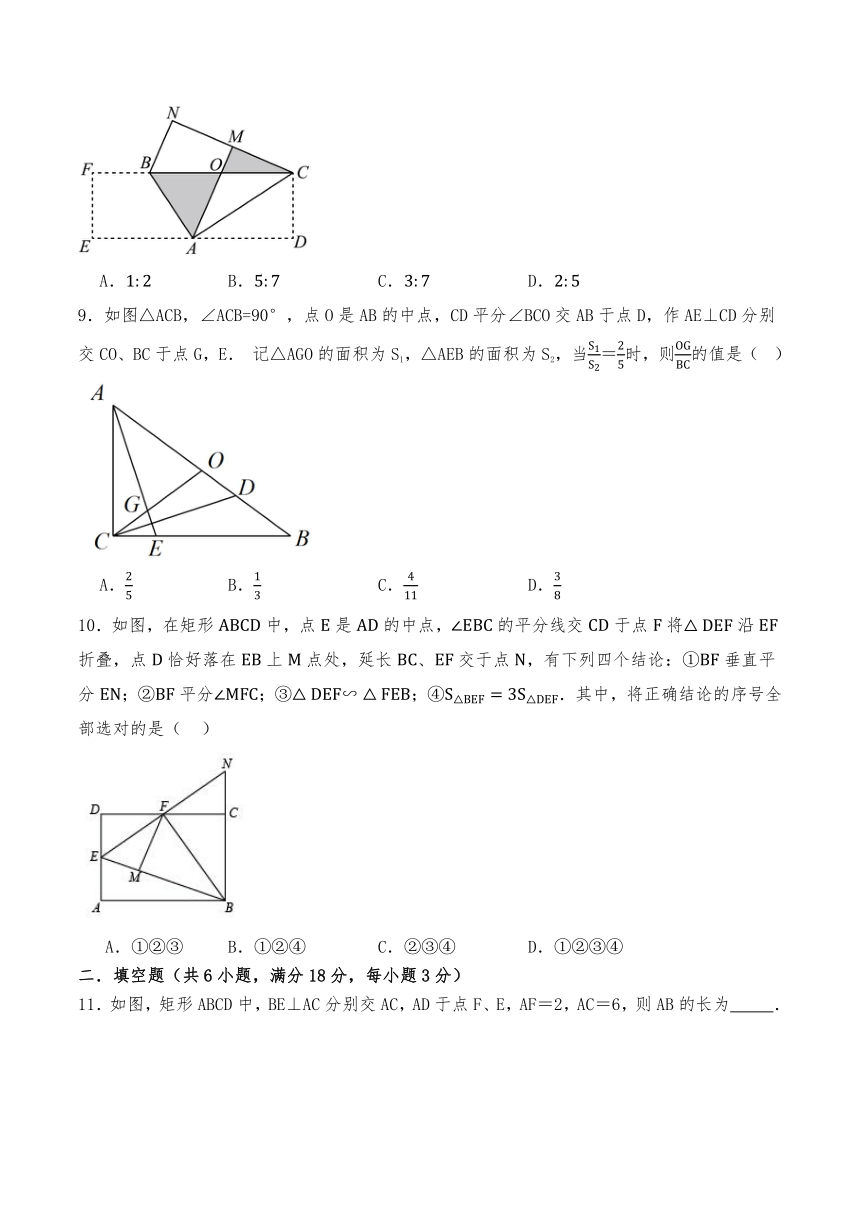
9.如图△ACB,∠ACB=90°,点O是AB的中点,CD平分∠BCO交AB于点D,作AE⊥CD分别交CO、BC于点G,E. 记△AGO的面积为S1,△AEB的面积为S2,当=时,则的值是( )
A. B. C. D.
10.如图,在矩形中,点是的中点,的平分线交于点将沿折叠,点恰好落在上点处,延长、交于点,有下列四个结论:①垂直平分;②平分;③;④.其中,将正确结论的序号全部选对的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
二.填空题(共6小题,满分18分,每小题3分)
11.如图,矩形ABCD中,BE⊥AC分别交AC,AD于点F、E,AF=2,AC=6,则AB的长为 .
12.黄金分割具有严格的比例性,蕴藏着丰富的美学价值,这一比值能够引起人们的美感.如图,连接正五边形ABCDE的各条对角线围成一个新的五边形MNPQR.图中有很多顶角为36°的等腰三角形,我们把这种三角形称为“黄金三角形”,黄金三角形的底与腰之比为.若MN=-1,则AB= .
13.如图,正方形的边长为4,点E在线段上,以为边构造正方形,使G在的延长线上,连接,取中点H,连接.当E为中点时,的面积为 ,当点E在边上运动(不含A,D)时,的最小值为 .
14.如图,在中,,,,为的中点,为线段上的动点,将沿过点的射线折叠得到,若下方的与的边垂直,则的长度可能是 .
15.在中,若AD交BC于D,BE交AC于E,CF交BA于F,AD,BE,CF相交于一点,,,则 .
16.已知菱形的边长为6,,对角线,相交于点O,以点O为坐标原点,分别以,所在直线为x轴、y轴,建立如图所示的直角坐标系.以为对角线作菱形菱形,再以为对角线作菱形菱形,再以为对角线作菱形菱形,…,按此规律继续作下去,在x轴的正半轴上得到点,,,…,,则点的坐标为 .
三.解答题(共7小题,满分52分)
17.(6分)求值:
(1)已知,求的值;
(2)已知,若,求的值.
18.(6分)如图,在的网格中,线段的端点都在格点上(两条网格线的交点叫格点).请用无刻度的直尺画出符合要求的图形,并保留画图痕迹(不要求写画法).
(1)在图1中画出一个以为边的,使顶点在格点上.
(2)在图2中的线段上找出一点,使.
19.(8分)如图所示,在等腰三角形中,,点E,F在线段上,,点Q在线段上,且.
求证:
(1);
(2).
20.(8分)已知在平面直角坐标系中的位置如图所示:
(1)在图中画出沿x轴翻折后的;
(2)以点为位似中心,作出按放大后的位似图形;
(3)点的坐标___________;与的周长比是___________,与的面积比是___________.
21.(8分)如图,在△ABC中,∠ACB=90°,CD是高,BE平分∠ABC.BE分别与AC,CD相交于点E,F.
(1)求证:△AEB∽△CFB;
(2)若CE=5,,BD=6.求AD的长.
22.(8分)【证明体验】
(1)如图1,为的角平分线,,点在线段上,,求证:平分;
【思考探究】
(2)如图2,在(1)的条件下,为上一点,连接交于点.若,
求证:;
【拓展延伸】
(3)如图3,在四边形中,对角线平分,,点在上,,若,,,求的长.
23.(8分)如图1,是等腰直角三角形,,先将边沿过点B的直线l对折得到,连接,然后以为边在左侧作,其中,,与交于点F,连接,.
(1)求证:;
(2)如图2,当点D在的斜边上时,请直接写出用表示的关系式;
(3)如图3,当点D在的内部时,若点F为的中点,且的面积为10,求的面积.
答案解析
一、选择题
1.B
【分析】对关系式化简为,分类讨论求出的值即可找出经过的象限.
【详解】 ,
,
当时,,
则,
此时直线为,过二、三、四象限.
当时,,
此时直线为,过一、二、三象限.
综上所述,过二、三象限.
故选B.
2.D
【分析】根据相似三角形的判定方法:两角分别对应相等的两个三角形相似;两边成比例且夹角相等的两个三角形相似;三边成比例的两个三角形相似;一条直角边与斜边成比例的两个直角三角形相似;逐一判断即可.
【详解】解∵,
∴,
若,,
∴,故A不符合题意;
若,,
∴,故B不符合题意;
若,,
∴,故C不符合题意;
∵,,
∴无法判断与相似,故D符合题意;
故选:D.
3.C
【分析】本题根据平行四边形的对边平行,再根据平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似找出相似三角形即可得解.
【详解】解:在 ABCD中,
∵AB∥CD,
∴△ABE∽△FDE,△ABG∽△FCG;
∵AD∥BC,
∴△ADE∽△GBE,△FDA∽△FCG,
∴△ABG∽△FDA,△ABD∽△BCD
∴图中相似三角形有6对.
故答案为6.
4.A
【分析】根据平行四边形的性质和平行线分线段成比例的性质进行解答即可.
【详解】解:四边形是平行四边形,
,,
,,故B错误,不符合题意;
,故A正确,符合题意;
如果,则有,
和不平行,
,故C错误,不符合题意;
如果,则有,
和不平行,
,故D错误,不符合题意;
故选:A.
5.B
【分析】如图,过点F作,交的延长线于点H,过点E作,交的延长线于点I,过点E作,垂足为G ,则四边形是矩形;运用勾股定理逆定理,求证,;求证从而求得 同理可证求得., 中,运用勾股定理求解.
【详解】解:如图,过点F作,交的延长线于点H,过点E作,交的延长线于点I,过点E作,垂足为G ,则四边形是矩形,
∴.
∵,
∴.
∴.
同理,.
∵,
∴.
∴
∴
∴
∴
同理,可证
∴.
∴.
∴.
∴中,.
故选:B
6.C
【分析】先根据折叠的性质与矩形性质,求得,设的长为x,则,再根据相似多边形性质得出,即,求解即可.
【详解】解:,由折叠可得:,,
∵矩形,
∴,
∴,
设的长为x,则,
∵矩形,
∴,
∵矩形与原矩形相似,
∴,即,
解得:(负值不符合题意,舍去)
∴,
故选:C.
7.A
【分析】先确定G点的坐标,再结合D点坐标和位似比为1:2,求出A点的坐标;然后再求出直线AG的解析式,直线AG与x的交点坐标,即为这两个三角形的位似中心的坐标..
【详解】解:∵△ADC与△EOG都是等腰直角三角形
∴OE=OG=1
∴G点的坐标分别为(0,-1)
∵D点坐标为D(2,0),位似比为1:2,
∴A点的坐标为(2,2)
∴直线AG的解析式为y=x-1
∴直线AG与x的交点坐标为(,0)
∴位似中心P点的坐标是.
故答案为A.
8.D
【分析】过点作于,过点作于点,则,根据相似三角形的性质得出,设,则,根据折叠的性质及矩形的性质推出,,,,则,根据三角形面积公式求解即可.
【详解】解:如图,过点作于,过点作于点,
,
,
,
,
,
设,则,
由折叠可知,,,,,,
,
四边形是矩形,
,,
,,,
,,
,
,
,
,
,,
,
故选:D.
9.D
【分析】连接BG,过点O作OT∥AE交BC于点T,首先证明,再利用平行线分线段成比例求解即可.
【详解】解:如图所示,连接BG,过点O作OT∥AE交BC于点T,
∵点O是AB的中点,
∴AO=OB,
∴,
∵,
∴,
∴,
∵OT∥AE,AO=BO,
∴ET=TB,
∴OT=AE,
∴,
∵AE⊥CD,CD平分∠BCO,
∴∠DCG=∠DCE,
∴∠CGE+∠DCG=90°,∠CEG+∠DCB=90°,
∴∠CGE=∠CEG,
∴CG=CE,
∵∠CGE=∠COT,∠CEG=∠CTD,
∴∠COT=∠CTD,
∴CO=CT,
∴OG=ET,
∵GE∥OT,
∴,
∴,
∴,
故选:D.
10.D
【分析】由折叠的性质、矩形的性质与角平分线的性质,可证得CF=FM=DF;易求得∠BFE=∠BFN,则可得BF⊥EN;证明∠EFM=∠EBF即可证明;易求得BM=2EM=2DE,即可得EB=3EM,根据等高三角形的面积比等于对应底的比,即可证明.
【详解】解:∵四边形ABCD是矩形,
∴∠D=∠BCD=90°,DF=MF,
由折叠的性质可得:∠EMF=∠D=90°,
即FM⊥BE,CF⊥BC,
∵BF平分∠EBC,
∴CF=MF,
∴DF=CF,在△DEF与△CFN中,
∴△DFE≌△CFN,
∴EF=FN,
∵∠BFM=90° ∠EBF,∠BFC=90° ∠CBF,
∴∠BFM=∠BFC,
∴BF平分∠MFC;故②正确;
∵∠MFE=∠DFE=∠CFN,
∴∠BFE=∠BFN,
∵∠BFE+∠BFN=180°,
∴∠BFE=90°,
即BF⊥EN,
∴BF垂直平分EN,故①正确;
∵∠BFE=∠D=∠FME=90°,
∴∠EFM+∠FEM=∠FEM+∠FBE=90°,
∴∠EFM=∠EBF,
∵∠DFE=∠EFM,
∴∠DFE=∠FBE,
∴;故③正确;
∵∠BFM=∠BFC,BM⊥FM,BC⊥CF,
∴BM=BC=AD=2DE=2EM,
∴BE=3EM,
∴S△BEF=3S△EMF=3S△DEF;
故④正确.
综上所述:①②③④都正确,
故答案选:D.
二.填空题
11.
【分析】根据题意,由矩形的性质综合判断得出∠ACB=∠ABF,∠BAF=∠BAC,从而证明△BFA∽△CBA,再利用相似三角形的性质列出方程,进而求解即可
【详解】解:∵BE⊥AC,
∴∠BAF+∠ABF=90°,
∵矩形ABCD中,∠ABC=90°,
∴∠ACB+∠BAF=90°,
∴∠ACB=∠ABF,
∵∠BAF=∠BAC,
∴△BFA∽△CBA,
∴,
∴AB2=AC AF=6×2=12,
∴.
故答案为.
12.+1
【详解】根据题意可知△DMN与△AME都是“黄金三角形”,AB=AE,DM=EM,
∴,,
∵MN=,
∴DM=2,
∴AE=,
∴AB=,
故答案为.
13. 2
【分析】当E为中点时,过点H作于点N,先证是的中位线,求出其长度,再根据三角形面积公式计算即可;连接,与交于点O,延长到点M,使,连接,根据正方形的性质先证点D、O、M、B在一条直线上,再证是的中位线,并推出当时,最小,根据正方形的性质得出,故点M与点O重合,求出对角线的长,即可得出的长,于是得出的长,再根据正方形的性质证,即可得出的最小值.
【详解】解:当E为中点时,过点H作于点N,如图1,
∵正方形的边长为4,
∴,
∴,
∵四边形是正方形,
∴,
∴,
∴,
∵点H是的中点,即,
∴,
∴点N是的中点,
∴是的中位线,
∴,
∴;
如图2,连接,与交于点O,延长到点M,使,连接,
∵四边形是正方形,
∴,
∴,
∴是等腰直角三角形,
∴,
∵四边形是正方形,
∴,
∴点D、O、M、B在一条直线上,
∵点E是的中点,点H是的中点,
∴是的中位线,
∴,
当最小时,最小,
即当时,最小,
∵,
∴M点与O点重合时,最小,
∵正方形的边长为4,
∴,
由勾股定理得,
∴,
∴,
∵四边形是正方形,
∴,
∵点H是的中点,
∴,
∴点H在的垂直平分线上,
∵四边形是正方形,
∴点H也在的垂直平分线上,
∴,
∴,
即的最小值为;
故答案为:2,.
14.2或或
【分析】由直角三角形的性质和勾股定理可得,,,分三种情况:当时,设垂足为;当时,作交于;当时,分别进行计算即可得到答案.
【详解】解:在中,,,
,
,
是的中点,
,
如图1,当时,设垂足为,
,
由折叠可知,,,,
,
,
,
,
,
,,
,
;
如图2,当时,
,
则,
由折叠可知:,
,
,
,
,
,
在中,,,
,
,,
作交于,则,
,
是等腰直角三角形,
,
设,则,
,
,
,即,
解得:,
,
在中,,,
;
如图3,当时,
,
由折叠的性质可得:,,,
,
,
,
,,
,
,
,
综上所述:的长为2或或,
故答案为:2或或.
15.
【分析】如图,先利用三角形的面积关系可得 ,,再结合比例的基本性质证明,可得,同理可得:, 可得, 从而可得结论.
【详解】解:如图,设AD,BE,CF相交于点,
, ,
,
,
同理可得: ,
,
,,
,
.
故答案为:
16.An(3n,0)
【分析】先根据菱形的性质求出A1的坐标,根据勾股定理求出OB1的长,再由锐角三角函数的定义求出OA2的长,故可得出A2的坐标,同理可得出A3的坐标,找出规律即可得出结论.
【详解】解:∵ 菱形的边长为6,,
∴OA1=A1B1·sin 30°=6×=3,OB1=A1B1·cos 30°=6×=,
∴A1(3,0),
∵ 菱形菱形,
∴OA2= ,
∴A2(9,0),
同理可得A3(27,0),
∴An(3n,0),
故答案为:An(3n,0).
三.解答题
17.(1)解:∵,
∴,
∴;
(2)解:∵,
∴,
∵,
∴,
∴.
18.(1)解:如下图,取格点C,连接和,
由题意可知:,
为;
(2)如下图,取格点E,F,连接交于点D,
由题意可知:,
,
,
点D即为所求.
19.(1)证明:∵,
∴,
在和中,,
∴,
∴;
(2)
证明:∵,
∴,,
∵,,
∴,即,
∴.
20.(1)解:如图,为所作;
(2)解:如图,为所作;
(3)解:点的坐标为,
∵沿x轴翻折后的,
∴,
∵按放大后的位似图形,
∴与的相似比为,
∴与的相似比为,
∴与的周长的比为,与的面积的比为.
故答案为:;;
21.(1)证明:,
,
为边上的高,
,
,
,
是的平分线,
,
.
(2)解:如图,作于.
∵∠BFD+∠ABE=90°,∠CEB+∠CBE=90°,∠ABE=∠CBE,
∴∠BFD=∠CEB,
∵∠BFD=∠CFE,
,
为等腰三角形,
,
,
∴点为的中点,
,
,
,
,
,
,
,,
,
,
根据,即,
,
,
,
,
.
22.(1)证明:∵为的角平分线
∴
∵,
∴
∴
∴
∴平分
(2)证明:∵
∴
∵
∴
∴,
由(1)可知:
∴
∴
(3)解:如图,在上取一点,使得,连接
∵平分
∴
∵
∴
∴
∵
∴
∵
∴
∴
∵
∴
∵,
∴
∴
∵
∴
解得:
∴
23.(1)证明:∵边沿过点B的直线l对折得到,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴;
(2)解:由(1)得:,
∴,
∴,
∵,
∴;
(3)解:如图,
设直线l交于点H,交于K,取的中点G,连接,
∵点F是的中点,
∴,
∴,
由折叠得:,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
由(1)知:,
∴,
∵点F是的中点,
∴,
∴.
一.选择题(共10小题,满分30分,每小题3分)
1.已知,则直线一定经过( )
A.第一、二象限 B.第二、三家限
C.第三、四象限 D.第一、四象限
2.如图,已知,添加下列条件后,仍无法判定的是( )
A. B. C. D.
3.如图,在中,点在的延长线上,分别交、于点、,则图中相似三角形共有( )
A.4对 B.5对 C.6对 D.7对
4.如图,在中,点在边上,连接,交于点.则下列结论正确的是( ).
A. B. C. D.
5.如图,正方形的边长是10,在正方形外有E、F两点,满足,,则EF的长是( )
A. B. C.14 D.
6.如图,四边形是一张矩形纸片.将其按如图所示的方式折叠:使边落在边上,点落在点处,折痕为;使边落在边上,点落在点处,折痕为.若矩形与原矩形相似,,则的长为( )
A. B. C. D.
7.如图,是由等腰直角经过位似变换得到的,位似中心在轴的正半轴,已知,点坐标为,位似比为,则两个三角形的位似中心点的坐标是( )
A. B. C. D.
8.如图,将长方形纸片分别沿,折叠,点D,E恰好重合于点M.记面积为,面积为,且,则的值为( )
A. B. C. D.
9.如图△ACB,∠ACB=90°,点O是AB的中点,CD平分∠BCO交AB于点D,作AE⊥CD分别交CO、BC于点G,E. 记△AGO的面积为S1,△AEB的面积为S2,当=时,则的值是( )
A. B. C. D.
10.如图,在矩形中,点是的中点,的平分线交于点将沿折叠,点恰好落在上点处,延长、交于点,有下列四个结论:①垂直平分;②平分;③;④.其中,将正确结论的序号全部选对的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
二.填空题(共6小题,满分18分,每小题3分)
11.如图,矩形ABCD中,BE⊥AC分别交AC,AD于点F、E,AF=2,AC=6,则AB的长为 .
12.黄金分割具有严格的比例性,蕴藏着丰富的美学价值,这一比值能够引起人们的美感.如图,连接正五边形ABCDE的各条对角线围成一个新的五边形MNPQR.图中有很多顶角为36°的等腰三角形,我们把这种三角形称为“黄金三角形”,黄金三角形的底与腰之比为.若MN=-1,则AB= .
13.如图,正方形的边长为4,点E在线段上,以为边构造正方形,使G在的延长线上,连接,取中点H,连接.当E为中点时,的面积为 ,当点E在边上运动(不含A,D)时,的最小值为 .
14.如图,在中,,,,为的中点,为线段上的动点,将沿过点的射线折叠得到,若下方的与的边垂直,则的长度可能是 .
15.在中,若AD交BC于D,BE交AC于E,CF交BA于F,AD,BE,CF相交于一点,,,则 .
16.已知菱形的边长为6,,对角线,相交于点O,以点O为坐标原点,分别以,所在直线为x轴、y轴,建立如图所示的直角坐标系.以为对角线作菱形菱形,再以为对角线作菱形菱形,再以为对角线作菱形菱形,…,按此规律继续作下去,在x轴的正半轴上得到点,,,…,,则点的坐标为 .
三.解答题(共7小题,满分52分)
17.(6分)求值:
(1)已知,求的值;
(2)已知,若,求的值.
18.(6分)如图,在的网格中,线段的端点都在格点上(两条网格线的交点叫格点).请用无刻度的直尺画出符合要求的图形,并保留画图痕迹(不要求写画法).
(1)在图1中画出一个以为边的,使顶点在格点上.
(2)在图2中的线段上找出一点,使.
19.(8分)如图所示,在等腰三角形中,,点E,F在线段上,,点Q在线段上,且.
求证:
(1);
(2).
20.(8分)已知在平面直角坐标系中的位置如图所示:
(1)在图中画出沿x轴翻折后的;
(2)以点为位似中心,作出按放大后的位似图形;
(3)点的坐标___________;与的周长比是___________,与的面积比是___________.
21.(8分)如图,在△ABC中,∠ACB=90°,CD是高,BE平分∠ABC.BE分别与AC,CD相交于点E,F.
(1)求证:△AEB∽△CFB;
(2)若CE=5,,BD=6.求AD的长.
22.(8分)【证明体验】
(1)如图1,为的角平分线,,点在线段上,,求证:平分;
【思考探究】
(2)如图2,在(1)的条件下,为上一点,连接交于点.若,
求证:;
【拓展延伸】
(3)如图3,在四边形中,对角线平分,,点在上,,若,,,求的长.
23.(8分)如图1,是等腰直角三角形,,先将边沿过点B的直线l对折得到,连接,然后以为边在左侧作,其中,,与交于点F,连接,.
(1)求证:;
(2)如图2,当点D在的斜边上时,请直接写出用表示的关系式;
(3)如图3,当点D在的内部时,若点F为的中点,且的面积为10,求的面积.
答案解析
一、选择题
1.B
【分析】对关系式化简为,分类讨论求出的值即可找出经过的象限.
【详解】 ,
,
当时,,
则,
此时直线为,过二、三、四象限.
当时,,
此时直线为,过一、二、三象限.
综上所述,过二、三象限.
故选B.
2.D
【分析】根据相似三角形的判定方法:两角分别对应相等的两个三角形相似;两边成比例且夹角相等的两个三角形相似;三边成比例的两个三角形相似;一条直角边与斜边成比例的两个直角三角形相似;逐一判断即可.
【详解】解∵,
∴,
若,,
∴,故A不符合题意;
若,,
∴,故B不符合题意;
若,,
∴,故C不符合题意;
∵,,
∴无法判断与相似,故D符合题意;
故选:D.
3.C
【分析】本题根据平行四边形的对边平行,再根据平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似找出相似三角形即可得解.
【详解】解:在 ABCD中,
∵AB∥CD,
∴△ABE∽△FDE,△ABG∽△FCG;
∵AD∥BC,
∴△ADE∽△GBE,△FDA∽△FCG,
∴△ABG∽△FDA,△ABD∽△BCD
∴图中相似三角形有6对.
故答案为6.
4.A
【分析】根据平行四边形的性质和平行线分线段成比例的性质进行解答即可.
【详解】解:四边形是平行四边形,
,,
,,故B错误,不符合题意;
,故A正确,符合题意;
如果,则有,
和不平行,
,故C错误,不符合题意;
如果,则有,
和不平行,
,故D错误,不符合题意;
故选:A.
5.B
【分析】如图,过点F作,交的延长线于点H,过点E作,交的延长线于点I,过点E作,垂足为G ,则四边形是矩形;运用勾股定理逆定理,求证,;求证从而求得 同理可证求得., 中,运用勾股定理求解.
【详解】解:如图,过点F作,交的延长线于点H,过点E作,交的延长线于点I,过点E作,垂足为G ,则四边形是矩形,
∴.
∵,
∴.
∴.
同理,.
∵,
∴.
∴
∴
∴
∴
同理,可证
∴.
∴.
∴.
∴中,.
故选:B
6.C
【分析】先根据折叠的性质与矩形性质,求得,设的长为x,则,再根据相似多边形性质得出,即,求解即可.
【详解】解:,由折叠可得:,,
∵矩形,
∴,
∴,
设的长为x,则,
∵矩形,
∴,
∵矩形与原矩形相似,
∴,即,
解得:(负值不符合题意,舍去)
∴,
故选:C.
7.A
【分析】先确定G点的坐标,再结合D点坐标和位似比为1:2,求出A点的坐标;然后再求出直线AG的解析式,直线AG与x的交点坐标,即为这两个三角形的位似中心的坐标..
【详解】解:∵△ADC与△EOG都是等腰直角三角形
∴OE=OG=1
∴G点的坐标分别为(0,-1)
∵D点坐标为D(2,0),位似比为1:2,
∴A点的坐标为(2,2)
∴直线AG的解析式为y=x-1
∴直线AG与x的交点坐标为(,0)
∴位似中心P点的坐标是.
故答案为A.
8.D
【分析】过点作于,过点作于点,则,根据相似三角形的性质得出,设,则,根据折叠的性质及矩形的性质推出,,,,则,根据三角形面积公式求解即可.
【详解】解:如图,过点作于,过点作于点,
,
,
,
,
,
设,则,
由折叠可知,,,,,,
,
四边形是矩形,
,,
,,,
,,
,
,
,
,
,,
,
故选:D.
9.D
【分析】连接BG,过点O作OT∥AE交BC于点T,首先证明,再利用平行线分线段成比例求解即可.
【详解】解:如图所示,连接BG,过点O作OT∥AE交BC于点T,
∵点O是AB的中点,
∴AO=OB,
∴,
∵,
∴,
∴,
∵OT∥AE,AO=BO,
∴ET=TB,
∴OT=AE,
∴,
∵AE⊥CD,CD平分∠BCO,
∴∠DCG=∠DCE,
∴∠CGE+∠DCG=90°,∠CEG+∠DCB=90°,
∴∠CGE=∠CEG,
∴CG=CE,
∵∠CGE=∠COT,∠CEG=∠CTD,
∴∠COT=∠CTD,
∴CO=CT,
∴OG=ET,
∵GE∥OT,
∴,
∴,
∴,
故选:D.
10.D
【分析】由折叠的性质、矩形的性质与角平分线的性质,可证得CF=FM=DF;易求得∠BFE=∠BFN,则可得BF⊥EN;证明∠EFM=∠EBF即可证明;易求得BM=2EM=2DE,即可得EB=3EM,根据等高三角形的面积比等于对应底的比,即可证明.
【详解】解:∵四边形ABCD是矩形,
∴∠D=∠BCD=90°,DF=MF,
由折叠的性质可得:∠EMF=∠D=90°,
即FM⊥BE,CF⊥BC,
∵BF平分∠EBC,
∴CF=MF,
∴DF=CF,在△DEF与△CFN中,
∴△DFE≌△CFN,
∴EF=FN,
∵∠BFM=90° ∠EBF,∠BFC=90° ∠CBF,
∴∠BFM=∠BFC,
∴BF平分∠MFC;故②正确;
∵∠MFE=∠DFE=∠CFN,
∴∠BFE=∠BFN,
∵∠BFE+∠BFN=180°,
∴∠BFE=90°,
即BF⊥EN,
∴BF垂直平分EN,故①正确;
∵∠BFE=∠D=∠FME=90°,
∴∠EFM+∠FEM=∠FEM+∠FBE=90°,
∴∠EFM=∠EBF,
∵∠DFE=∠EFM,
∴∠DFE=∠FBE,
∴;故③正确;
∵∠BFM=∠BFC,BM⊥FM,BC⊥CF,
∴BM=BC=AD=2DE=2EM,
∴BE=3EM,
∴S△BEF=3S△EMF=3S△DEF;
故④正确.
综上所述:①②③④都正确,
故答案选:D.
二.填空题
11.
【分析】根据题意,由矩形的性质综合判断得出∠ACB=∠ABF,∠BAF=∠BAC,从而证明△BFA∽△CBA,再利用相似三角形的性质列出方程,进而求解即可
【详解】解:∵BE⊥AC,
∴∠BAF+∠ABF=90°,
∵矩形ABCD中,∠ABC=90°,
∴∠ACB+∠BAF=90°,
∴∠ACB=∠ABF,
∵∠BAF=∠BAC,
∴△BFA∽△CBA,
∴,
∴AB2=AC AF=6×2=12,
∴.
故答案为.
12.+1
【详解】根据题意可知△DMN与△AME都是“黄金三角形”,AB=AE,DM=EM,
∴,,
∵MN=,
∴DM=2,
∴AE=,
∴AB=,
故答案为.
13. 2
【分析】当E为中点时,过点H作于点N,先证是的中位线,求出其长度,再根据三角形面积公式计算即可;连接,与交于点O,延长到点M,使,连接,根据正方形的性质先证点D、O、M、B在一条直线上,再证是的中位线,并推出当时,最小,根据正方形的性质得出,故点M与点O重合,求出对角线的长,即可得出的长,于是得出的长,再根据正方形的性质证,即可得出的最小值.
【详解】解:当E为中点时,过点H作于点N,如图1,
∵正方形的边长为4,
∴,
∴,
∵四边形是正方形,
∴,
∴,
∴,
∵点H是的中点,即,
∴,
∴点N是的中点,
∴是的中位线,
∴,
∴;
如图2,连接,与交于点O,延长到点M,使,连接,
∵四边形是正方形,
∴,
∴,
∴是等腰直角三角形,
∴,
∵四边形是正方形,
∴,
∴点D、O、M、B在一条直线上,
∵点E是的中点,点H是的中点,
∴是的中位线,
∴,
当最小时,最小,
即当时,最小,
∵,
∴M点与O点重合时,最小,
∵正方形的边长为4,
∴,
由勾股定理得,
∴,
∴,
∵四边形是正方形,
∴,
∵点H是的中点,
∴,
∴点H在的垂直平分线上,
∵四边形是正方形,
∴点H也在的垂直平分线上,
∴,
∴,
即的最小值为;
故答案为:2,.
14.2或或
【分析】由直角三角形的性质和勾股定理可得,,,分三种情况:当时,设垂足为;当时,作交于;当时,分别进行计算即可得到答案.
【详解】解:在中,,,
,
,
是的中点,
,
如图1,当时,设垂足为,
,
由折叠可知,,,,
,
,
,
,
,
,,
,
;
如图2,当时,
,
则,
由折叠可知:,
,
,
,
,
,
在中,,,
,
,,
作交于,则,
,
是等腰直角三角形,
,
设,则,
,
,
,即,
解得:,
,
在中,,,
;
如图3,当时,
,
由折叠的性质可得:,,,
,
,
,
,,
,
,
,
综上所述:的长为2或或,
故答案为:2或或.
15.
【分析】如图,先利用三角形的面积关系可得 ,,再结合比例的基本性质证明,可得,同理可得:, 可得, 从而可得结论.
【详解】解:如图,设AD,BE,CF相交于点,
, ,
,
,
同理可得: ,
,
,,
,
.
故答案为:
16.An(3n,0)
【分析】先根据菱形的性质求出A1的坐标,根据勾股定理求出OB1的长,再由锐角三角函数的定义求出OA2的长,故可得出A2的坐标,同理可得出A3的坐标,找出规律即可得出结论.
【详解】解:∵ 菱形的边长为6,,
∴OA1=A1B1·sin 30°=6×=3,OB1=A1B1·cos 30°=6×=,
∴A1(3,0),
∵ 菱形菱形,
∴OA2= ,
∴A2(9,0),
同理可得A3(27,0),
∴An(3n,0),
故答案为:An(3n,0).
三.解答题
17.(1)解:∵,
∴,
∴;
(2)解:∵,
∴,
∵,
∴,
∴.
18.(1)解:如下图,取格点C,连接和,
由题意可知:,
为;
(2)如下图,取格点E,F,连接交于点D,
由题意可知:,
,
,
点D即为所求.
19.(1)证明:∵,
∴,
在和中,,
∴,
∴;
(2)
证明:∵,
∴,,
∵,,
∴,即,
∴.
20.(1)解:如图,为所作;
(2)解:如图,为所作;
(3)解:点的坐标为,
∵沿x轴翻折后的,
∴,
∵按放大后的位似图形,
∴与的相似比为,
∴与的相似比为,
∴与的周长的比为,与的面积的比为.
故答案为:;;
21.(1)证明:,
,
为边上的高,
,
,
,
是的平分线,
,
.
(2)解:如图,作于.
∵∠BFD+∠ABE=90°,∠CEB+∠CBE=90°,∠ABE=∠CBE,
∴∠BFD=∠CEB,
∵∠BFD=∠CFE,
,
为等腰三角形,
,
,
∴点为的中点,
,
,
,
,
,
,
,,
,
,
根据,即,
,
,
,
,
.
22.(1)证明:∵为的角平分线
∴
∵,
∴
∴
∴
∴平分
(2)证明:∵
∴
∵
∴
∴,
由(1)可知:
∴
∴
(3)解:如图,在上取一点,使得,连接
∵平分
∴
∵
∴
∴
∵
∴
∵
∴
∴
∵
∴
∵,
∴
∴
∵
∴
解得:
∴
23.(1)证明:∵边沿过点B的直线l对折得到,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴;
(2)解:由(1)得:,
∴,
∴,
∵,
∴;
(3)解:如图,
设直线l交于点H,交于K,取的中点G,连接,
∵点F是的中点,
∴,
∴,
由折叠得:,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
由(1)知:,
∴,
∵点F是的中点,
∴,
∴.
