2024天津市中考数学模拟3(含答案)
图片预览




文档简介
中小学教育资源及组卷应用平台
2024年天津市初中学业水平考试数学模拟3
本试卷分为第Ⅰ卷(选择题)、第Ⅱ卷(非选择题)两部分。第Ⅰ卷为第1页至第3页,第Ⅱ卷为第4页至第8页。试卷满分120分。考试时间100分钟。
答卷前,请你务必将自己的姓名、考生号、考点校、考场号、座位号填写在“答题卡”上,并在规定位置粘贴考试用条形码。答题时,务必将答案涂写在“答题卡”上,答案答在试卷上无效。考试结束后,将本试卷和“答题卡”一并交回。
祝你考试顺利!
第Ⅰ卷
注意事项:
1.每题选出答案后,用2B铅笔把“答题卡”上对应题目的答案标号的信息点涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号的信息点。
2.本卷共12题,共36分。
一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.计算﹣6﹣12÷3的结果等于( )
A.6 B.﹣2 C.﹣6 D.﹣10
2.估计﹣2的值( )
A.在2到3之间 B.在3到4之间
C.在4到5之间 D.在5到6之间
3.如图,是由一个圆柱体和一个长方体组成的几何体,其俯视图是( )
A. B. C. D.
4.2022年4月16日神舟十三号载人飞船圆满完成全部既定任务,顺利返回地球家园.六个月的飞天之旅展现了中国航天科技的新高度下列航天图标,其文字上方的图案是中心对称图形的是( )
A.B.C. D.
5.2024年全国普通高校毕业生规模预计达到1179万人,将1179万用科学记数法表示为( )
A.1.179×107 B.1.179×108 C.1.179×103 D.1179×104
6.计算cos30°﹣的值( )
A.0 B. C.1 D.
7.计算的结果是( )
A. B. C. D.
8.已知关于x的一元二次方程x2+4x+3=0的两根分别为a、b,则的值为( )
A. B. C.﹣ D.﹣
9.若反比例函数的图象经过点(3,﹣5),则它的图象一定还经过点( )
A.(3,5) B.(﹣1,16) C.(﹣3,﹣5) D.(﹣15,1)
10.如图,已知在纸上有一点O.按下列尺规作图的步骤进行:
①以点O为圆心,以任意长r为半径,画半圆O,直径为AB;
②分别以点O,B为圆心,大于OB长为半径作弧,两弧交于点M,N,作直线MN,交半圆O于点C;
③连接OC,以点C为圆心,以OC长为半径作弧,交半圆O于点E,连接AE,CE.
下列结论不正确的是( )
A.四边形AOCE是菱形
B.四边形AOCE的面积为r2
C.∠EAB=60°
D.E是的中点
11.如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=114°,则∠α的大小是( )
A.68° B.20° C.24° D.22°
12.如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.若设AD的长度为x米,矩形菜园ABCD面积为S平方米.下列说法错误的是( )
A.S与x的关系式为
B.当a=20,S=450时,x=10
C.当a=60,x=50时,S=1250
D.不论a为何值,S的最大值均为1250
第Ⅱ卷
注意事项:
1.用黑色字迹的签字笔将答案写在“答题卡”上(作图可用2B铅笔)。
2.本卷共13题,共84分。
二、填空题(本大题共6小题,每小题3分,共18分)
13.一个不透明的袋子里装有4个红球和6个黑球,它们除颜色外其余都相同,从袋中任意摸出一个球是黑球的概率为 .
14.计算:(5x3)2= .
15.计算(4+)(4﹣)的结果等于 .
16.若将直线y=2x+1的图象先向左平移3个单位,再向下平移4个单位所得直线解析式是 .
17.如图,在正方形ABCD中,AC=,E,F分别是边AD,CD上的点,且AE=DF.AF,DE交于点O,P为AB的中点,则
1)∠AOB=___________°
2)OP=______________
18.如图,在每个小正方形的边长为1的网格中,△ABC内接于圆,且顶点A,B,C都是格点,点N在圆上且不在网格线上,连接AN.
(Ⅰ)线段AC的长等于 ;
(Ⅱ)在圆上找点M,满足弦AM=AN,请用无刻度的直尺,在如图所示的网格中,画出点M,并简要说明它的位置是如何找到的(不要求证明) _____________________________________
____________________________________________________________________________________
三、解答题(本大题共7小题,共66分.解答应写出文字说明、演算步骤或推理过程)
19.(本小题8分)
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得______;
(Ⅱ)解不等式②,得______;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
(Ⅳ)原不等式组的解集为______.
20.(本小题8分)
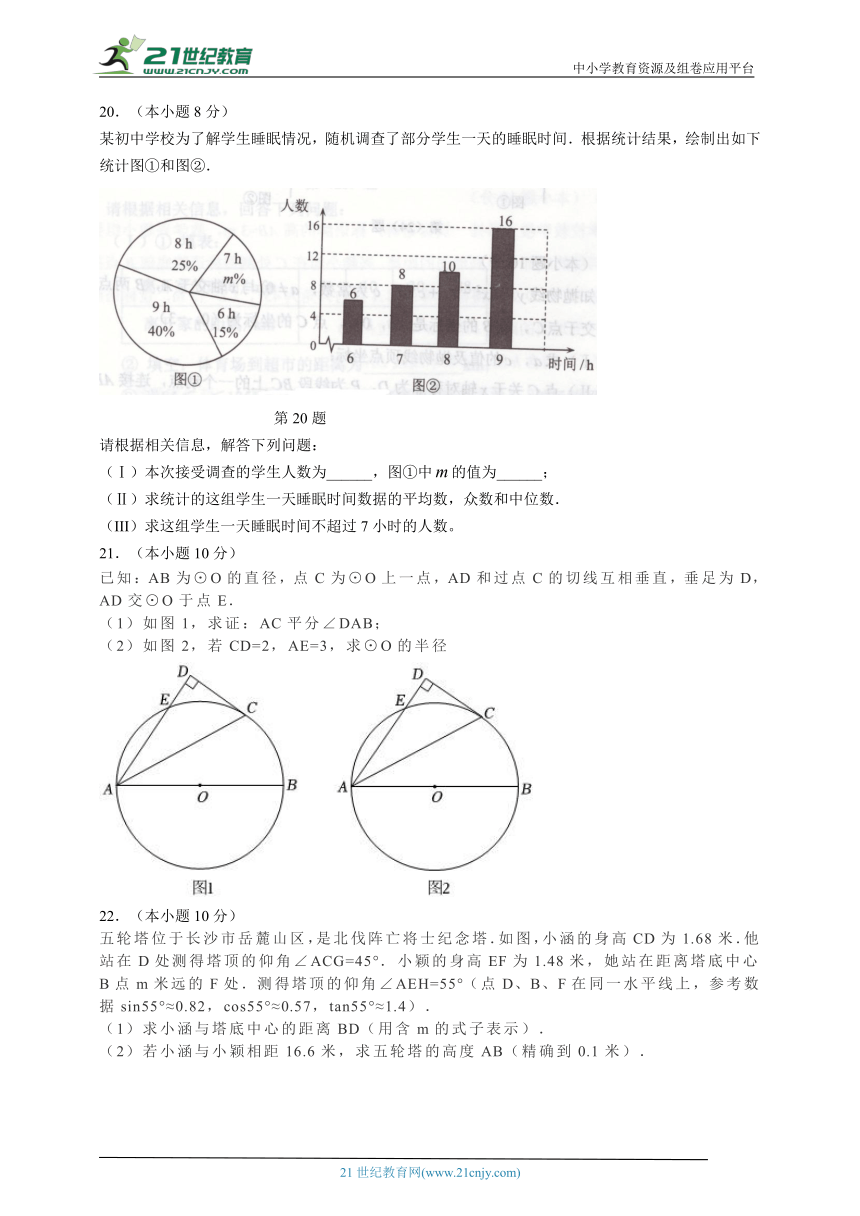
某初中学校为了解学生睡眠情况,随机调查了部分学生一天的睡眠时间.根据统计结果,绘制出如下统计图①和图②.
第20题
请根据相关信息,解答下列问题:
(Ⅰ)本次接受调查的学生人数为______,图①中的值为______;
(Ⅱ)求统计的这组学生一天睡眠时间数据的平均数,众数和中位数.
(III)求这组学生一天睡眠时间不超过7小时的人数。
21.(本小题10分)
已知:AB为⊙O的直径,点C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D,AD交⊙O于点E.
(1)如图1,求证:AC平分∠DAB;
(2)如图2,若CD=2,AE=3,求⊙O的半径
22.(本小题10分)
五轮塔位于长沙市岳麓山区,是北伐阵亡将士纪念塔.如图,小涵的身高CD为1.68米.他站在D处测得塔顶的仰角∠ACG=45°.小颖的身高EF为1.48米,她站在距离塔底中心B点m米远的F处.测得塔顶的仰角∠AEH=55°(点D、B、F在同一水平线上,参考数据sin55°≈0.82,cos55°≈0.57,tan55°≈1.4).
(1)求小涵与塔底中心的距离BD(用含m的式子表示).
(2)若小涵与小颖相距16.6米,求五轮塔的高度AB(精确到0.1米).
23.(本小题10分)
假定甲、乙、丙三地依次在一条直线上,甲乙两地间的距离为280km,乙丙两地之间的距离为140km.一艘游轮从甲地出发前往丙地,途中经过乙地停留时,一艘货轮也沿着同样的线路从甲地出发前往丙地.已知游轮的速度为20km/h,游轮从甲地到达丙地共用了23小时.若将游轮行驶的时间记为t(h),两艘轮船距离甲地的路程s(km)关于t(h)的图象如图所示(游轮在停靠前后的行驶速度不变).
(Ⅰ)写出游轮从甲地到乙地所用的时长__________;游轮在乙地停留的时长_______
(Ⅱ)直接写出游轮在行驶的过程中s关于t的函数解析式;
(Ⅲ)若货轮比游轮早36分钟到达丙地,则货轮出发后几小时追上游轮?
24.(本小题10分)
将一个矩形纸片ABCD放置在平面直角坐标系中,点O(0,0),点B(6,0),点D(﹣3,,AD与y轴相交于点M,点Q在边AD上(点Q不与点A,D重合),折叠该纸片,使折痕所在的直线经过点Q,并与x轴相交于点P,且∠QPB=60°,点A,B的对应点分别为点A′,B′.
(Ⅰ)如图①,当点B′落在线段OM上时,求∠OB′P的大小和点B′的坐标;
(Ⅱ)设BP=t,纸片折叠后与矩形OCDM的重叠部分的面积为S.
①如图②,若折叠后与矩形OCDM的重叠部分是四边形时,B′P与边OM相交于点E,试用含有t的式子表示B′E的长,并直接写出t的取值范围;
②当时,求S的取值范围(直接写出结果即可).
25.(本小题10分)
如图,抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于点C,顶点为D.其中A(﹣3,0),D(﹣1,﹣4).
(1)直接写出该抛物线的解析式;
(2)如图1,在第三象限内抛物线上找点E,使∠OCE=∠OAD,求点E的坐标;
(3)如图2,过抛物线对称轴上点P的直线交抛物线于F,G两点,线段FG的中点是M,过点M作y轴的平行线交抛物线于点N.若是一个定值,求点P的坐标.
2024年天津市初中学业水平考试数学模拟3
答案:1-5:D.B.C.B.A.6-10:A.A.D.D.B.11-12:C.D.
13. .14. 25x6 .15. 13 .16. y=2x+3 .
17.如图,在正方形ABCD中,AC=,E,F分别是边AD,CD上的点,且AE=DF.AF,DE交于点O,P为AB的中点,则1)∠AOB=90°2)OP= .
【解答】解:∵四边形ABCD是正方形,∴AD=AB,∠D=∠EAB=90°,AC=AB,
∴AB=AC=×=1,在△ADF和△BAE中,,
∴△ADF≌△BAE(SAS),∴∠DAF=∠ABE,∵∠DAF+∠BAO=90°,
∴∠ABE+∠BAO=90°,∴∠AOB=90°,∵P为AB的中点,∴OP=AB=;故答案为:.
18.如图,在每个小正方形的边长为1的网格中,△ABC内接于圆,且顶点A,B,C都是格点,点N在圆上且不在网格线上,连接AN.
(Ⅰ)线段AC的长等于 5 ;
(Ⅱ)在圆上找点M,满足弦AM=AN,请用无刻度的直尺,在如图所示的网格中,画出点M,并简要说明它的位置是如何找到的(不要求证明) 取格点P,连接BP与圆相交于点Q,连接BN与AC相交于点D,连接QD并延长与圆相交于点M,点M即为所求 .
【解答】解:(Ⅰ)由图知,,
故答案为:5.
(Ⅱ)所作点M如图所示:
取格点P,连接BP与圆相交于点Q,连接BN与AC相交于点D,连接QD并延长与圆相交于点M,点M即为所求.
故答案为:取格点P,连接BP与圆相交于点Q,连接BN与AC相交于点D,连接QD并延长与圆相交于点M,点M即为所求.
三、解答题(本大题共7小题,共66分.解答应写出文字说明、演算步骤或推理过程)
19.(本小题8分)
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得______;
(Ⅱ)解不等式②,得______;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
(Ⅳ)原不等式组的解集为______.
20.(本小题8分)
某初中学校为了解学生睡眠情况,随机调查了部分学生一天的睡眠时间.根据统计结果,绘制出如下统计图①和图②.
第20题
请根据相关信息,解答下列问题:
(Ⅰ)本次接受调查的学生人数为__40____,图①中的值为___20___;
(Ⅱ)求统计的这组学生一天睡眠时间数据的平均数,众数和中位数.
平均数:7.9h; 众数:9h; 中位数:8h;
21.(本小题10分)
已知:AB为⊙O的直径,点C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D,AD交⊙O于点E.
(1)如图1,求证:AC平分∠DAB;
(2)如图2,若CD=2,AE=3,求⊙O的半径
(1)证明:连接OC,如图1,∵CD为⊙O的切线,∴OC⊥CD,∵AD⊥CD,
∴OC∥AD,∵CD为⊙O的切线,∴OC⊥CD,∵AD⊥CD,∴OC∥AD,
∴∠DAC=∠OCA,∵OA=OC,∴∠OAC=∠OCA,∴∠DAC=∠OAC,∴AC平分∠DAB;
(2)解:连接BE交OC于F点,如图2,
∵AB为⊙O的直径,∴∠AEF=90°,∵∠DEF=∠D=∠FCD=90°,
∴四边形CDEF为矩形,∴EF=CD=2,∠CFE=90°,∴OF⊥BE,
∴BF=EF=2,在Rt△ABE中,AB=
√ AE2+BE2
=
√ 32+42
=5,
∴⊙O的半径为2.5
22.(本小题10分)
五轮塔位于长沙市岳麓山区,是北伐阵亡将士纪念塔.如图,小涵的身高CD为1.68米.他站在D处测得塔顶的仰角∠ACG=45°.小颖的身高EF为1.48米,她站在距离塔底中心B点m米远的F处.测得塔顶的仰角∠AEH=55°(点D、B、F在同一水平线上,参考数据sin55°≈0.82,cos55°≈0.57,tan55°≈1.4).
(1)求小涵与塔底中心的距离BD(用含m的式子表示).
(2)若小涵与小颖相距16.6米,求五轮塔的高度AB(精确到0.1米).
23.(本小题10分)
假定甲、乙、丙三地依次在一条直线上,甲乙两地间的距离为280km,乙丙两地之间的距离为140km.一艘游轮从甲地出发前往丙地,途中经过乙地停留时,一艘货轮也沿着同样的线路从甲地出发前往丙地.已知游轮的速度为20km/h,游轮从甲地到达丙地共用了23小时.若将游轮行驶的时间记为t(h),两艘轮船距离甲地的路程s(km)关于t(h)的图象如图所示(游轮在停靠前后的行驶速度不变).
(Ⅰ)写出游轮从甲地到乙地所用的时长__________;游轮在乙地停留的时长_______
(Ⅱ)直接写出游轮在行驶的过程中s关于t的函数解析式;
(Ⅲ)若货轮比游轮早36分钟到达丙地,则货轮出发后几小时追上游轮?
解:(1)游轮从甲地到乙地所用的时间为:280÷20=14(小时),
游轮从乙地到丙地所用的时间为:140÷20=7(小时),
∵游轮从甲地到丙地共用了23小时,
∴游轮在乙地停留的时间为:23-14-7=2(小时),
故答案为:14,2;
(2)由(1)得:A点坐标为:(14,280),
∵游轮到乙地后停留2小时,
∴B的坐标为:(16,280),C的坐标为:(23,420),
设OA段的解析式为:s=kt(k≠0),
∴280=14k,
解得:k=20,
∴s=20t(0≤t≤14),
AB段的解析式为:s=280(14≤t≤16),
设BC段的解析式为s=k1t+b(k1≠0),
∴
16k1+b=28023k1+b=420
,
解得:
k1=20b= 40
,
∴BC段的解析式为s=20t-40(16<t≤23);
(3)由题意得,游轮出发14小时后,货轮再出发,且比游轮早36分钟到达丙地,
36分钟=0.6小时,
∴货轮行驶的时间为:23-14-0.6=8.4(小时),
∴货轮的速度为:420÷8.4=50(km/h),
设货轮出发后x小时追上游轮,则游轮行驶的时间为:14+x-2=(12+x)小时,
∴20(12+x)=50x,
解得:x=8,
答:货轮出发8小时追上游轮.
24.(本小题10分)
将一个矩形纸片ABCD放置在平面直角坐标系中,点O(0,0),点B(6,0),点D(﹣3,,AD与y轴相交于点M,点Q在边AD上(点Q不与点A,D重合),折叠该纸片,使折痕所在的直线经过点Q,并与x轴相交于点P,且∠QPB=60°,点A,B的对应点分别为点A′,B′.
(Ⅰ)如图①,当点B′落在线段OM上时,求∠OB′P的大小和点B′的坐标;
(Ⅱ)设BP=t,纸片折叠后与矩形OCDM的重叠部分的面积为S.
①如图②,若折叠后与矩形OCDM的重叠部分是四边形时,B′P与边OM相交于点E,试用含有t的式子表示B′E的长,并直接写出t的取值范围;
②当时,求S的取值范围(直接写出结果即可).
【解答】解:(1)由折叠的性质可得:
∠BPQ=∠QPB=60°,PB'=PB,
∠OPB'=180°﹣∠B'PQ﹣∠QPB=60°
∠OB'P=90°﹣∠OPB'=30°,
在Rt△OPB'中,PB=2OP,OB'=OP,
∵OB=OP+PB=OP+PB'=3OP=6,
∴OP=2,0B'=OP=2,
∴点B'的坐标为:B'(0,2);
(2)①∵BP=t,
∴OP=OB﹣BP=6一t,
由折叠的性质可得:∠B'PQ=∠QPB=60°,
PB'=PB=t,
∠OPB'=180°﹣∠B'PQ﹣∠QPB=60°
∠OBP=90°﹣∠OPB'=30°,在Rt△OPE中,
PE=2OP=2(6﹣t)=12﹣2t,
OE=OP﹣(6﹣t)=6﹣t,
BE=PB'﹣PE=t﹣(12﹣2t)=3t﹣12
t的取值范围是:5<t<6;
②当t=时,S==,
当6≤t≤9时,
S=3×﹣(t﹣6)×(t﹣6)﹣(9﹣t)×(9﹣t)
=﹣(t﹣)2+
当t=时,S为最大值,
故答案为:.
25.(本小题10分)
如图,抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于点C,顶点为D.其中A(﹣3,0),D(﹣1,﹣4).
(1)直接写出该抛物线的解析式;
(2)如图1,在第三象限内抛物线上找点E,使∠OCE=∠OAD,求点E的坐标;
(3)如图2,过抛物线对称轴上点P的直线交抛物线于F,G两点,线段FG的中点是M,过点M作y轴的平行线交抛物线于点N.若是一个定值,求点P的坐标.
【解答】解:(1)抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于点C,顶点为D.其中A(﹣3,0),D(﹣1,﹣4),将A,D两点坐标代入得:
∴,
解得,
∴该抛物线的解析式为y=x2+2x﹣3;
(2)在第三象限内抛物线上找点E,使∠OCE=∠OAD,如图1,过点E作EF⊥y轴于F,过点D作DG⊥x轴于G,则∠EFC=∠DGA=90°,
∵A(﹣3,0),D(﹣1,﹣4),
∴AG=﹣1﹣(﹣3)=2,DG=4,
把x=0代入y=x2+2x﹣3得,y=﹣3,
∴C(0,﹣3),
∴OC=3,
设点E(m,m2+2m﹣3),则EF=﹣m,OF=﹣(m2+2m﹣3),
∴CF=OC﹣OF=3+(m2+2m﹣3)=m2+2m,
∵∠OCE=∠OAD,
∴tan∠OCE=tan∠OAD,
∴,
即,
整理得,2m2+5m=0,
解得或m2=0(不合,舍去),
∴;
(3)过抛物线对称轴上点P的直线交抛物线于F,G两点,线段FG的中点是M,过点M作y轴的平行线交抛物线于点N.如图2,设P(﹣1,t),
设直线FG的解析式为:y=kx+b,
∴t=﹣k+b,即b=k+t,
∴直线FG的解析式为:y=kx+k+t,
设F(x1,y1),G(x2,y2),
由,得x2+2x﹣3=kx+k+t,即:x2+(2﹣k)x﹣3﹣k﹣t=0,
∴x1+x2=k﹣2,x1x2=﹣3﹣k﹣t,
∴
=
∵线段FG的中点是M,
∴,,
∴,
∴,
∴,
∴当4t+15=0时,即时,是定值,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2024年天津市初中学业水平考试数学模拟3
本试卷分为第Ⅰ卷(选择题)、第Ⅱ卷(非选择题)两部分。第Ⅰ卷为第1页至第3页,第Ⅱ卷为第4页至第8页。试卷满分120分。考试时间100分钟。
答卷前,请你务必将自己的姓名、考生号、考点校、考场号、座位号填写在“答题卡”上,并在规定位置粘贴考试用条形码。答题时,务必将答案涂写在“答题卡”上,答案答在试卷上无效。考试结束后,将本试卷和“答题卡”一并交回。
祝你考试顺利!
第Ⅰ卷
注意事项:
1.每题选出答案后,用2B铅笔把“答题卡”上对应题目的答案标号的信息点涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号的信息点。
2.本卷共12题,共36分。
一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.计算﹣6﹣12÷3的结果等于( )
A.6 B.﹣2 C.﹣6 D.﹣10
2.估计﹣2的值( )
A.在2到3之间 B.在3到4之间
C.在4到5之间 D.在5到6之间
3.如图,是由一个圆柱体和一个长方体组成的几何体,其俯视图是( )
A. B. C. D.
4.2022年4月16日神舟十三号载人飞船圆满完成全部既定任务,顺利返回地球家园.六个月的飞天之旅展现了中国航天科技的新高度下列航天图标,其文字上方的图案是中心对称图形的是( )
A.B.C. D.
5.2024年全国普通高校毕业生规模预计达到1179万人,将1179万用科学记数法表示为( )
A.1.179×107 B.1.179×108 C.1.179×103 D.1179×104
6.计算cos30°﹣的值( )
A.0 B. C.1 D.
7.计算的结果是( )
A. B. C. D.
8.已知关于x的一元二次方程x2+4x+3=0的两根分别为a、b,则的值为( )
A. B. C.﹣ D.﹣
9.若反比例函数的图象经过点(3,﹣5),则它的图象一定还经过点( )
A.(3,5) B.(﹣1,16) C.(﹣3,﹣5) D.(﹣15,1)
10.如图,已知在纸上有一点O.按下列尺规作图的步骤进行:
①以点O为圆心,以任意长r为半径,画半圆O,直径为AB;
②分别以点O,B为圆心,大于OB长为半径作弧,两弧交于点M,N,作直线MN,交半圆O于点C;
③连接OC,以点C为圆心,以OC长为半径作弧,交半圆O于点E,连接AE,CE.
下列结论不正确的是( )
A.四边形AOCE是菱形
B.四边形AOCE的面积为r2
C.∠EAB=60°
D.E是的中点
11.如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=114°,则∠α的大小是( )
A.68° B.20° C.24° D.22°
12.如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.若设AD的长度为x米,矩形菜园ABCD面积为S平方米.下列说法错误的是( )
A.S与x的关系式为
B.当a=20,S=450时,x=10
C.当a=60,x=50时,S=1250
D.不论a为何值,S的最大值均为1250
第Ⅱ卷
注意事项:
1.用黑色字迹的签字笔将答案写在“答题卡”上(作图可用2B铅笔)。
2.本卷共13题,共84分。
二、填空题(本大题共6小题,每小题3分,共18分)
13.一个不透明的袋子里装有4个红球和6个黑球,它们除颜色外其余都相同,从袋中任意摸出一个球是黑球的概率为 .
14.计算:(5x3)2= .
15.计算(4+)(4﹣)的结果等于 .
16.若将直线y=2x+1的图象先向左平移3个单位,再向下平移4个单位所得直线解析式是 .
17.如图,在正方形ABCD中,AC=,E,F分别是边AD,CD上的点,且AE=DF.AF,DE交于点O,P为AB的中点,则
1)∠AOB=___________°
2)OP=______________
18.如图,在每个小正方形的边长为1的网格中,△ABC内接于圆,且顶点A,B,C都是格点,点N在圆上且不在网格线上,连接AN.
(Ⅰ)线段AC的长等于 ;
(Ⅱ)在圆上找点M,满足弦AM=AN,请用无刻度的直尺,在如图所示的网格中,画出点M,并简要说明它的位置是如何找到的(不要求证明) _____________________________________
____________________________________________________________________________________
三、解答题(本大题共7小题,共66分.解答应写出文字说明、演算步骤或推理过程)
19.(本小题8分)
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得______;
(Ⅱ)解不等式②,得______;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
(Ⅳ)原不等式组的解集为______.
20.(本小题8分)
某初中学校为了解学生睡眠情况,随机调查了部分学生一天的睡眠时间.根据统计结果,绘制出如下统计图①和图②.
第20题
请根据相关信息,解答下列问题:
(Ⅰ)本次接受调查的学生人数为______,图①中的值为______;
(Ⅱ)求统计的这组学生一天睡眠时间数据的平均数,众数和中位数.
(III)求这组学生一天睡眠时间不超过7小时的人数。
21.(本小题10分)
已知:AB为⊙O的直径,点C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D,AD交⊙O于点E.
(1)如图1,求证:AC平分∠DAB;
(2)如图2,若CD=2,AE=3,求⊙O的半径
22.(本小题10分)
五轮塔位于长沙市岳麓山区,是北伐阵亡将士纪念塔.如图,小涵的身高CD为1.68米.他站在D处测得塔顶的仰角∠ACG=45°.小颖的身高EF为1.48米,她站在距离塔底中心B点m米远的F处.测得塔顶的仰角∠AEH=55°(点D、B、F在同一水平线上,参考数据sin55°≈0.82,cos55°≈0.57,tan55°≈1.4).
(1)求小涵与塔底中心的距离BD(用含m的式子表示).
(2)若小涵与小颖相距16.6米,求五轮塔的高度AB(精确到0.1米).
23.(本小题10分)
假定甲、乙、丙三地依次在一条直线上,甲乙两地间的距离为280km,乙丙两地之间的距离为140km.一艘游轮从甲地出发前往丙地,途中经过乙地停留时,一艘货轮也沿着同样的线路从甲地出发前往丙地.已知游轮的速度为20km/h,游轮从甲地到达丙地共用了23小时.若将游轮行驶的时间记为t(h),两艘轮船距离甲地的路程s(km)关于t(h)的图象如图所示(游轮在停靠前后的行驶速度不变).
(Ⅰ)写出游轮从甲地到乙地所用的时长__________;游轮在乙地停留的时长_______
(Ⅱ)直接写出游轮在行驶的过程中s关于t的函数解析式;
(Ⅲ)若货轮比游轮早36分钟到达丙地,则货轮出发后几小时追上游轮?
24.(本小题10分)
将一个矩形纸片ABCD放置在平面直角坐标系中,点O(0,0),点B(6,0),点D(﹣3,,AD与y轴相交于点M,点Q在边AD上(点Q不与点A,D重合),折叠该纸片,使折痕所在的直线经过点Q,并与x轴相交于点P,且∠QPB=60°,点A,B的对应点分别为点A′,B′.
(Ⅰ)如图①,当点B′落在线段OM上时,求∠OB′P的大小和点B′的坐标;
(Ⅱ)设BP=t,纸片折叠后与矩形OCDM的重叠部分的面积为S.
①如图②,若折叠后与矩形OCDM的重叠部分是四边形时,B′P与边OM相交于点E,试用含有t的式子表示B′E的长,并直接写出t的取值范围;
②当时,求S的取值范围(直接写出结果即可).
25.(本小题10分)
如图,抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于点C,顶点为D.其中A(﹣3,0),D(﹣1,﹣4).
(1)直接写出该抛物线的解析式;
(2)如图1,在第三象限内抛物线上找点E,使∠OCE=∠OAD,求点E的坐标;
(3)如图2,过抛物线对称轴上点P的直线交抛物线于F,G两点,线段FG的中点是M,过点M作y轴的平行线交抛物线于点N.若是一个定值,求点P的坐标.
2024年天津市初中学业水平考试数学模拟3
答案:1-5:D.B.C.B.A.6-10:A.A.D.D.B.11-12:C.D.
13. .14. 25x6 .15. 13 .16. y=2x+3 .
17.如图,在正方形ABCD中,AC=,E,F分别是边AD,CD上的点,且AE=DF.AF,DE交于点O,P为AB的中点,则1)∠AOB=90°2)OP= .
【解答】解:∵四边形ABCD是正方形,∴AD=AB,∠D=∠EAB=90°,AC=AB,
∴AB=AC=×=1,在△ADF和△BAE中,,
∴△ADF≌△BAE(SAS),∴∠DAF=∠ABE,∵∠DAF+∠BAO=90°,
∴∠ABE+∠BAO=90°,∴∠AOB=90°,∵P为AB的中点,∴OP=AB=;故答案为:.
18.如图,在每个小正方形的边长为1的网格中,△ABC内接于圆,且顶点A,B,C都是格点,点N在圆上且不在网格线上,连接AN.
(Ⅰ)线段AC的长等于 5 ;
(Ⅱ)在圆上找点M,满足弦AM=AN,请用无刻度的直尺,在如图所示的网格中,画出点M,并简要说明它的位置是如何找到的(不要求证明) 取格点P,连接BP与圆相交于点Q,连接BN与AC相交于点D,连接QD并延长与圆相交于点M,点M即为所求 .
【解答】解:(Ⅰ)由图知,,
故答案为:5.
(Ⅱ)所作点M如图所示:
取格点P,连接BP与圆相交于点Q,连接BN与AC相交于点D,连接QD并延长与圆相交于点M,点M即为所求.
故答案为:取格点P,连接BP与圆相交于点Q,连接BN与AC相交于点D,连接QD并延长与圆相交于点M,点M即为所求.
三、解答题(本大题共7小题,共66分.解答应写出文字说明、演算步骤或推理过程)
19.(本小题8分)
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得______;
(Ⅱ)解不等式②,得______;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
(Ⅳ)原不等式组的解集为______.
20.(本小题8分)
某初中学校为了解学生睡眠情况,随机调查了部分学生一天的睡眠时间.根据统计结果,绘制出如下统计图①和图②.
第20题
请根据相关信息,解答下列问题:
(Ⅰ)本次接受调查的学生人数为__40____,图①中的值为___20___;
(Ⅱ)求统计的这组学生一天睡眠时间数据的平均数,众数和中位数.
平均数:7.9h; 众数:9h; 中位数:8h;
21.(本小题10分)
已知:AB为⊙O的直径,点C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D,AD交⊙O于点E.
(1)如图1,求证:AC平分∠DAB;
(2)如图2,若CD=2,AE=3,求⊙O的半径
(1)证明:连接OC,如图1,∵CD为⊙O的切线,∴OC⊥CD,∵AD⊥CD,
∴OC∥AD,∵CD为⊙O的切线,∴OC⊥CD,∵AD⊥CD,∴OC∥AD,
∴∠DAC=∠OCA,∵OA=OC,∴∠OAC=∠OCA,∴∠DAC=∠OAC,∴AC平分∠DAB;
(2)解:连接BE交OC于F点,如图2,
∵AB为⊙O的直径,∴∠AEF=90°,∵∠DEF=∠D=∠FCD=90°,
∴四边形CDEF为矩形,∴EF=CD=2,∠CFE=90°,∴OF⊥BE,
∴BF=EF=2,在Rt△ABE中,AB=
√ AE2+BE2
=
√ 32+42
=5,
∴⊙O的半径为2.5
22.(本小题10分)
五轮塔位于长沙市岳麓山区,是北伐阵亡将士纪念塔.如图,小涵的身高CD为1.68米.他站在D处测得塔顶的仰角∠ACG=45°.小颖的身高EF为1.48米,她站在距离塔底中心B点m米远的F处.测得塔顶的仰角∠AEH=55°(点D、B、F在同一水平线上,参考数据sin55°≈0.82,cos55°≈0.57,tan55°≈1.4).
(1)求小涵与塔底中心的距离BD(用含m的式子表示).
(2)若小涵与小颖相距16.6米,求五轮塔的高度AB(精确到0.1米).
23.(本小题10分)
假定甲、乙、丙三地依次在一条直线上,甲乙两地间的距离为280km,乙丙两地之间的距离为140km.一艘游轮从甲地出发前往丙地,途中经过乙地停留时,一艘货轮也沿着同样的线路从甲地出发前往丙地.已知游轮的速度为20km/h,游轮从甲地到达丙地共用了23小时.若将游轮行驶的时间记为t(h),两艘轮船距离甲地的路程s(km)关于t(h)的图象如图所示(游轮在停靠前后的行驶速度不变).
(Ⅰ)写出游轮从甲地到乙地所用的时长__________;游轮在乙地停留的时长_______
(Ⅱ)直接写出游轮在行驶的过程中s关于t的函数解析式;
(Ⅲ)若货轮比游轮早36分钟到达丙地,则货轮出发后几小时追上游轮?
解:(1)游轮从甲地到乙地所用的时间为:280÷20=14(小时),
游轮从乙地到丙地所用的时间为:140÷20=7(小时),
∵游轮从甲地到丙地共用了23小时,
∴游轮在乙地停留的时间为:23-14-7=2(小时),
故答案为:14,2;
(2)由(1)得:A点坐标为:(14,280),
∵游轮到乙地后停留2小时,
∴B的坐标为:(16,280),C的坐标为:(23,420),
设OA段的解析式为:s=kt(k≠0),
∴280=14k,
解得:k=20,
∴s=20t(0≤t≤14),
AB段的解析式为:s=280(14≤t≤16),
设BC段的解析式为s=k1t+b(k1≠0),
∴
16k1+b=28023k1+b=420
,
解得:
k1=20b= 40
,
∴BC段的解析式为s=20t-40(16<t≤23);
(3)由题意得,游轮出发14小时后,货轮再出发,且比游轮早36分钟到达丙地,
36分钟=0.6小时,
∴货轮行驶的时间为:23-14-0.6=8.4(小时),
∴货轮的速度为:420÷8.4=50(km/h),
设货轮出发后x小时追上游轮,则游轮行驶的时间为:14+x-2=(12+x)小时,
∴20(12+x)=50x,
解得:x=8,
答:货轮出发8小时追上游轮.
24.(本小题10分)
将一个矩形纸片ABCD放置在平面直角坐标系中,点O(0,0),点B(6,0),点D(﹣3,,AD与y轴相交于点M,点Q在边AD上(点Q不与点A,D重合),折叠该纸片,使折痕所在的直线经过点Q,并与x轴相交于点P,且∠QPB=60°,点A,B的对应点分别为点A′,B′.
(Ⅰ)如图①,当点B′落在线段OM上时,求∠OB′P的大小和点B′的坐标;
(Ⅱ)设BP=t,纸片折叠后与矩形OCDM的重叠部分的面积为S.
①如图②,若折叠后与矩形OCDM的重叠部分是四边形时,B′P与边OM相交于点E,试用含有t的式子表示B′E的长,并直接写出t的取值范围;
②当时,求S的取值范围(直接写出结果即可).
【解答】解:(1)由折叠的性质可得:
∠BPQ=∠QPB=60°,PB'=PB,
∠OPB'=180°﹣∠B'PQ﹣∠QPB=60°
∠OB'P=90°﹣∠OPB'=30°,
在Rt△OPB'中,PB=2OP,OB'=OP,
∵OB=OP+PB=OP+PB'=3OP=6,
∴OP=2,0B'=OP=2,
∴点B'的坐标为:B'(0,2);
(2)①∵BP=t,
∴OP=OB﹣BP=6一t,
由折叠的性质可得:∠B'PQ=∠QPB=60°,
PB'=PB=t,
∠OPB'=180°﹣∠B'PQ﹣∠QPB=60°
∠OBP=90°﹣∠OPB'=30°,在Rt△OPE中,
PE=2OP=2(6﹣t)=12﹣2t,
OE=OP﹣(6﹣t)=6﹣t,
BE=PB'﹣PE=t﹣(12﹣2t)=3t﹣12
t的取值范围是:5<t<6;
②当t=时,S==,
当6≤t≤9时,
S=3×﹣(t﹣6)×(t﹣6)﹣(9﹣t)×(9﹣t)
=﹣(t﹣)2+
当t=时,S为最大值,
故答案为:.
25.(本小题10分)
如图,抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于点C,顶点为D.其中A(﹣3,0),D(﹣1,﹣4).
(1)直接写出该抛物线的解析式;
(2)如图1,在第三象限内抛物线上找点E,使∠OCE=∠OAD,求点E的坐标;
(3)如图2,过抛物线对称轴上点P的直线交抛物线于F,G两点,线段FG的中点是M,过点M作y轴的平行线交抛物线于点N.若是一个定值,求点P的坐标.
【解答】解:(1)抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于点C,顶点为D.其中A(﹣3,0),D(﹣1,﹣4),将A,D两点坐标代入得:
∴,
解得,
∴该抛物线的解析式为y=x2+2x﹣3;
(2)在第三象限内抛物线上找点E,使∠OCE=∠OAD,如图1,过点E作EF⊥y轴于F,过点D作DG⊥x轴于G,则∠EFC=∠DGA=90°,
∵A(﹣3,0),D(﹣1,﹣4),
∴AG=﹣1﹣(﹣3)=2,DG=4,
把x=0代入y=x2+2x﹣3得,y=﹣3,
∴C(0,﹣3),
∴OC=3,
设点E(m,m2+2m﹣3),则EF=﹣m,OF=﹣(m2+2m﹣3),
∴CF=OC﹣OF=3+(m2+2m﹣3)=m2+2m,
∵∠OCE=∠OAD,
∴tan∠OCE=tan∠OAD,
∴,
即,
整理得,2m2+5m=0,
解得或m2=0(不合,舍去),
∴;
(3)过抛物线对称轴上点P的直线交抛物线于F,G两点,线段FG的中点是M,过点M作y轴的平行线交抛物线于点N.如图2,设P(﹣1,t),
设直线FG的解析式为:y=kx+b,
∴t=﹣k+b,即b=k+t,
∴直线FG的解析式为:y=kx+k+t,
设F(x1,y1),G(x2,y2),
由,得x2+2x﹣3=kx+k+t,即:x2+(2﹣k)x﹣3﹣k﹣t=0,
∴x1+x2=k﹣2,x1x2=﹣3﹣k﹣t,
∴
=
∵线段FG的中点是M,
∴,,
∴,
∴,
∴,
∴当4t+15=0时,即时,是定值,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
