21.1 锐角三角函数 课件(北京课改版九年级上)
文档属性
| 名称 | 21.1 锐角三角函数 课件(北京课改版九年级上) |

|
|
| 格式 | rar | ||
| 文件大小 | 60.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-21 00:00:00 | ||
图片预览






文档简介
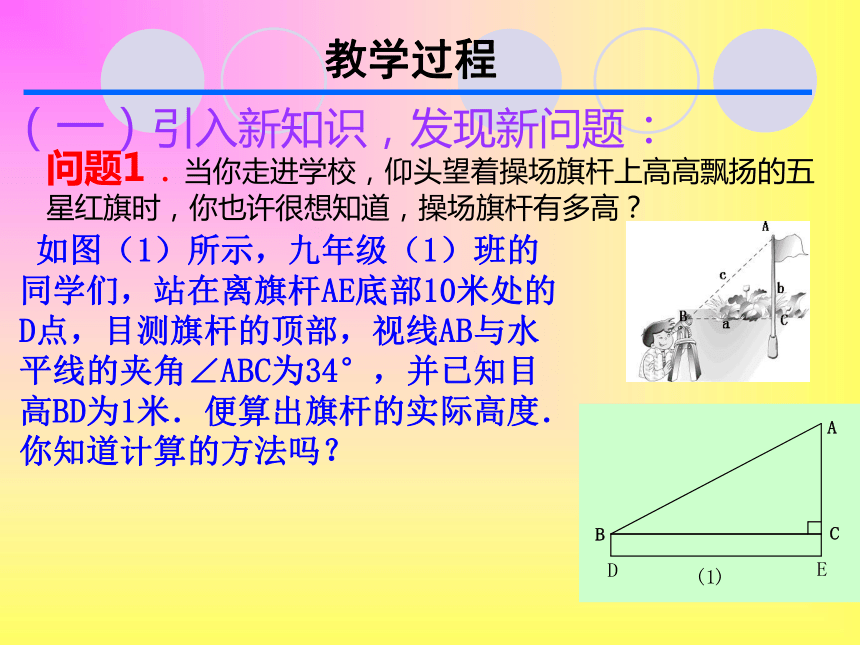
课件15张PPT。§21.1锐角三角函数(一)教学过程 (一)引入新知识,发现新问题:问题1.当你走进学校,仰头望着操场旗杆上高高飘扬的五星红旗时,你也许很想知道,操场旗杆有多高? 如图(1)所示,九年级(1)班的
同学们,站在离旗杆AE底部10米处的
D点,目测旗杆的顶部,视线AB与水
平线的夹角∠ABC为34°,并已知目
高BD为1米.便算出旗杆的实际高度.
你知道计算的方法吗? 问题2.九年级(2)班的同学们,来到天安门广场测量人民英雄纪念碑的高度.他们的方法是:如图:CD表示人民英雄纪念碑的高度,
首先用1.5米高的支架AA’、BB’和三角板确定点A和
点B的位置,使得A、B、C在同一条直线上,
∠DA’C’=45°, ∠DB’C’=60°, A’ B’交DC于点C’,
然后测量出AB的长为16米.根据这些
数据,他们就计算出了CD的长.你知
道他们是怎样计算的吗?
(二)整体感知新知识: 做一做: 已知:在Rt△ABC中,∠C=90°.
(1)若∠A =30°,则∠A所对的直角边与斜边
的比=_______.
(2)若∠A=45°, 则∠A所对的直角边与斜边之
比=_______.
(3)若∠A=60°, 则∠A所对的直角边与斜边之
比=_______. 教学过程 当∠A =30°时,当∠A =60°时,当∠A =45°时,教学过程 想一想:一般情况下,在Rt△ABC中,当锐角A取其他固定值时,∠A的对边与邻边的比值还会是一个固定值吗?明确:在Rt△ABC中,对于锐角任意的一个值,它
的对边与斜边的比都是一个固定不变的值,
与Rt△ABC的大小无关.(三)归纳概念:教学过程 在△ABC中,∠C=90°,我们把锐角A的对边与斜边的
比叫做∠A的正弦,记作sinA, 指出:“sinA”是一个完整的符号,不要误解成 ,记号
里习惯省去角的符号“∠”. 单独写出符号sin是没有意义的,
因为它离开了确定的锐角无法显示它的含义.例1:教学过程 已知:在Rt△ABC中,∠C=90°,AC=3,
BC=4,求sinA和sinB的值..例1的设置是为了巩固正弦概念,通过教师示范,使学生会求锐角的正弦.例2:已知:如图,在△ABC中,∠C=90°,
sinA= ,BC=3,求AB、AC的值. 说明:学生独立思考,小组交流解题思路,
师生共同寻求解题方法。 教学过程 变式:已知:如图,在△ABC中,∠C=90°,
sinA= ,求sinB的值。1.(03宁夏)在Rt△ABC中,如果各边长度都
扩大2倍,那么锐角A的正弦值( )
A.没有变化 B. 扩大2倍
C.缩小2倍 D. 不能确定教学过程 (四)熟练概念、灵活应用:中考链接(快速抢答): 2.(04海淀)在△ABC中,∠C=90°,BC=5,
AB=13,那么sinA的值等于( ).
A. B. C. D.教学过程 4.(03海南)在△ABC中,C=90°, ,则BC∶AC的值等于( )
A. 3∶4 B. 4∶3 C. 3∶5 D. 4∶5 3. (04年大连)在Rt△ABC中,∠C=90°,a = 1 ,
c = 4 , 则sinB的值是 ( )
A. B. C. D.教学过程 5.在Rt△ABC中,∠C=900,a:b=1: ,
则c= a,sinA= ,sinB= ;
6.在Rt△ABC中,∠C=900,a= ,三角形
的面积为 ,则斜边长是 ,sinA= ;教学过程 (五)课堂小结:学生小结本节课都学会了什么?还有什么疑问?你还想知道什么?
1.引导学生作知识总结:本节课通过动手实
验、证明,我们发现,只要直角三角形的
锐角固定,它的对边与斜边的比值是固定
的.
2.体会这种研究问题的方法。(六)布置作业
1.课本P92 练习 2,3
2.思考:结合右图,思考∠A的其他两边的比值是
不是也是唯一确定的?发挥你的聪明才智,动手
试一试.谢谢!
同学们,站在离旗杆AE底部10米处的
D点,目测旗杆的顶部,视线AB与水
平线的夹角∠ABC为34°,并已知目
高BD为1米.便算出旗杆的实际高度.
你知道计算的方法吗? 问题2.九年级(2)班的同学们,来到天安门广场测量人民英雄纪念碑的高度.他们的方法是:如图:CD表示人民英雄纪念碑的高度,
首先用1.5米高的支架AA’、BB’和三角板确定点A和
点B的位置,使得A、B、C在同一条直线上,
∠DA’C’=45°, ∠DB’C’=60°, A’ B’交DC于点C’,
然后测量出AB的长为16米.根据这些
数据,他们就计算出了CD的长.你知
道他们是怎样计算的吗?
(二)整体感知新知识: 做一做: 已知:在Rt△ABC中,∠C=90°.
(1)若∠A =30°,则∠A所对的直角边与斜边
的比=_______.
(2)若∠A=45°, 则∠A所对的直角边与斜边之
比=_______.
(3)若∠A=60°, 则∠A所对的直角边与斜边之
比=_______. 教学过程 当∠A =30°时,当∠A =60°时,当∠A =45°时,教学过程 想一想:一般情况下,在Rt△ABC中,当锐角A取其他固定值时,∠A的对边与邻边的比值还会是一个固定值吗?明确:在Rt△ABC中,对于锐角任意的一个值,它
的对边与斜边的比都是一个固定不变的值,
与Rt△ABC的大小无关.(三)归纳概念:教学过程 在△ABC中,∠C=90°,我们把锐角A的对边与斜边的
比叫做∠A的正弦,记作sinA, 指出:“sinA”是一个完整的符号,不要误解成 ,记号
里习惯省去角的符号“∠”. 单独写出符号sin是没有意义的,
因为它离开了确定的锐角无法显示它的含义.例1:教学过程 已知:在Rt△ABC中,∠C=90°,AC=3,
BC=4,求sinA和sinB的值..例1的设置是为了巩固正弦概念,通过教师示范,使学生会求锐角的正弦.例2:已知:如图,在△ABC中,∠C=90°,
sinA= ,BC=3,求AB、AC的值. 说明:学生独立思考,小组交流解题思路,
师生共同寻求解题方法。 教学过程 变式:已知:如图,在△ABC中,∠C=90°,
sinA= ,求sinB的值。1.(03宁夏)在Rt△ABC中,如果各边长度都
扩大2倍,那么锐角A的正弦值( )
A.没有变化 B. 扩大2倍
C.缩小2倍 D. 不能确定教学过程 (四)熟练概念、灵活应用:中考链接(快速抢答): 2.(04海淀)在△ABC中,∠C=90°,BC=5,
AB=13,那么sinA的值等于( ).
A. B. C. D.教学过程 4.(03海南)在△ABC中,C=90°, ,则BC∶AC的值等于( )
A. 3∶4 B. 4∶3 C. 3∶5 D. 4∶5 3. (04年大连)在Rt△ABC中,∠C=90°,a = 1 ,
c = 4 , 则sinB的值是 ( )
A. B. C. D.教学过程 5.在Rt△ABC中,∠C=900,a:b=1: ,
则c= a,sinA= ,sinB= ;
6.在Rt△ABC中,∠C=900,a= ,三角形
的面积为 ,则斜边长是 ,sinA= ;教学过程 (五)课堂小结:学生小结本节课都学会了什么?还有什么疑问?你还想知道什么?
1.引导学生作知识总结:本节课通过动手实
验、证明,我们发现,只要直角三角形的
锐角固定,它的对边与斜边的比值是固定
的.
2.体会这种研究问题的方法。(六)布置作业
1.课本P92 练习 2,3
2.思考:结合右图,思考∠A的其他两边的比值是
不是也是唯一确定的?发挥你的聪明才智,动手
试一试.谢谢!
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
