21.2锐角的三角函数值课件(北京教改版九年级上)
文档属性
| 名称 | 21.2锐角的三角函数值课件(北京教改版九年级上) |

|
|
| 格式 | rar | ||
| 文件大小 | 635.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-21 00:00:00 | ||
图片预览




文档简介
课件21张PPT。 21.2
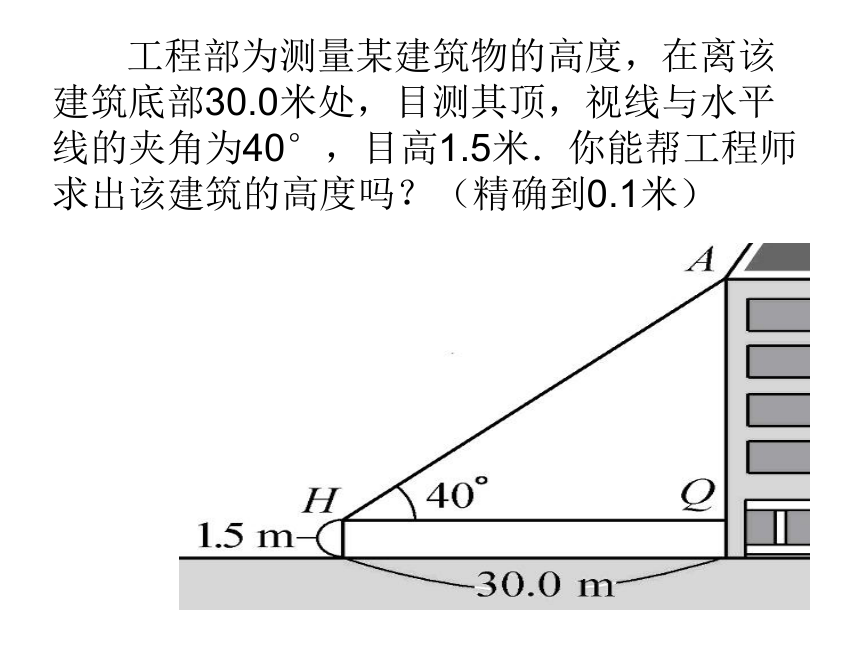
锐角的三角函数值 工程部为测量某建筑物的高度,在离该建筑底部30.0米处,目测其顶,视线与水平线的夹角为40°,目高1.5米.你能帮工程师求出该建筑的高度吗?(精确到0.1米)直角三角形中边角的再认识如图,Rt△ABC中: 找一找
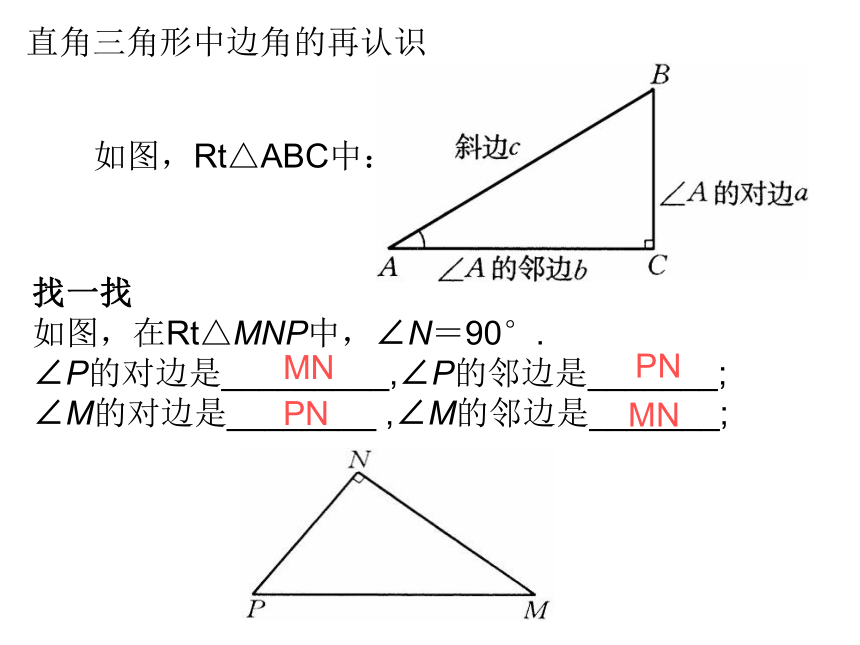
如图,在Rt△MNP中,∠N=90°.
∠P的对边是_________,∠P的邻边是_______;
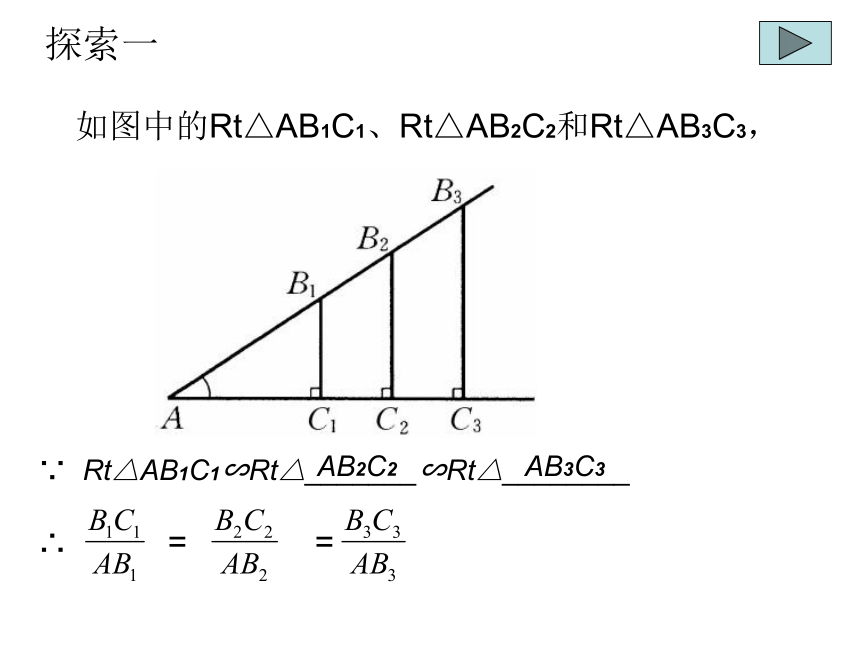
∠M的对边是________ ,∠M的邻边是_______;MNPNPNMN如图中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3,
∵ Rt△AB1C1∽Rt△_______∽Rt△________
∴ = =AB3C3AB2C2探索一思考:
在Rt△ABC中,对于锐角A的每一个确定的值,
①∠A的对边与斜边的比值与△ABC的边长大小有关系吗? ②∠A的邻边与斜边的比值呢?
③∠A的对边与邻边的比值呢?
④∠A的邻边与对边的比值呢?
由此可见:
在Rt△ABC中,对于锐角A的每一个确定的值,其对边与斜边、邻边与斜边、对边与邻边、邻边与对边的比值是惟一确定的.
在一个变化过程中,有两个变量X和Y,对于X的每一个值,Y都有惟一的值与之对应,我们就说X是自变量,Y是因变量,此时也称Y是X的函数。????????? 这几个比值都是锐角∠A的函数,记作
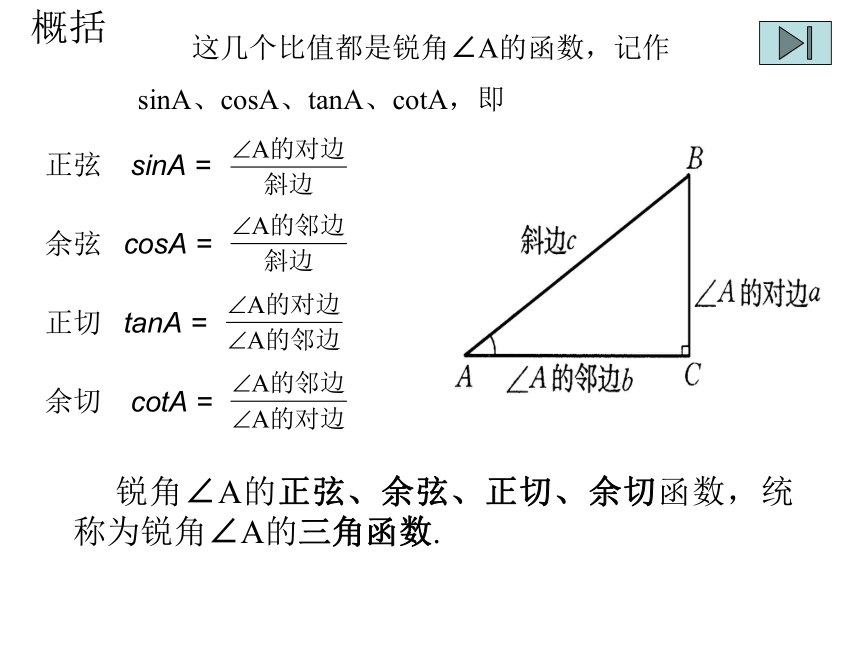
sinA、cosA、tanA、cotA,即
sinA = cosA = tanA = cotA = 锐角∠A的正弦、余弦、正切、余切函数,统称为锐角∠A的三角函数.
概括正弦余弦正切余切例 求出如图所示的Rt△ABC中∠A的四个三角函数值. 解:∵ ∴ sinA = cosA = tanA = cotA = 17 求出如图所示的Rt△DEC(∠E=90°)中∠D的四个三角函数值.
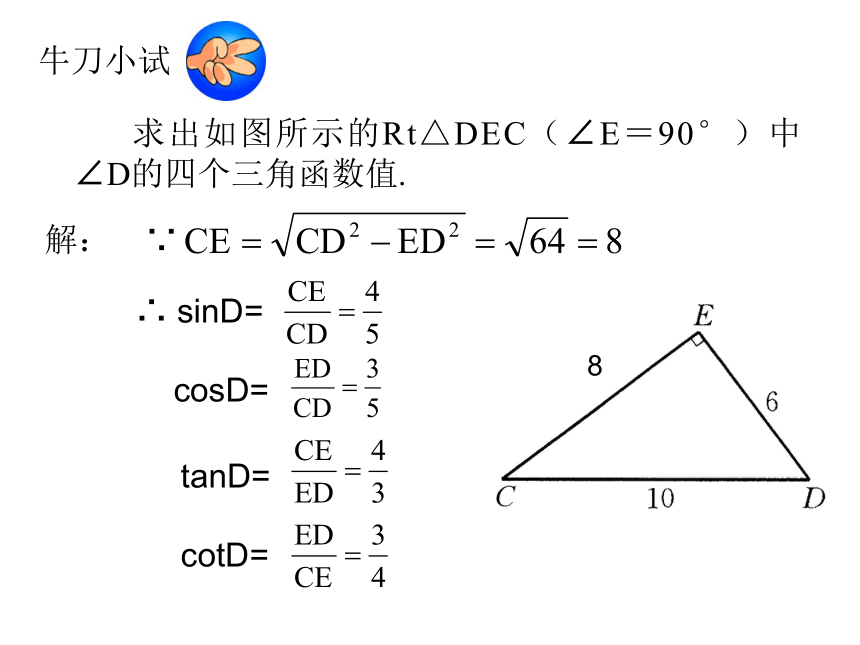
牛刀小试 解: ∵ ∴ sinD=
cosD= tanD= cotD= 8探索二(1)根据三角函数的定义,sin30°是一个常数.用刻度尺量出你所用的含30°的三角尺中,30°所对的直角边与斜边的长,与同桌交流,看看这个常数是什么.sin30°=
即斜边等于对边的2倍. 因此我们还可以得到:
在直角三角形中,如果一个锐角等于30°,
那么它所对的直角边等于斜边的一半.
∴ BC= ∵ ∠C=90 °, ∠A=30 °
AB(直角三角形中30 °角所对的直角边等于斜边的一半 )几何论证 (2)根据sin30°= , 怎样求cos30°、tan30°、cot30°的值呢?
cos30°= tan30°= cot30°= sin60°= cos60°= tan60°= cot60°= (3)== (4)用类似的方法求sin45°、cos45°、tan45°、 cot45°的值,并完成课本P109的表格。 sin45°= cos45°= tan45°=
cot45°= 11(5)根据表格,思考以下问题: 问题1:自变量α的取值范围是____________,各因变量的取值范围呢? ??
0°<α< 90° 正弦 0< sinα<1
余弦 0< cosα<1
正切 tanα>0
余切 cotα>0
问题2:各个函数值随着自变量α的增大而怎样变化? sinα、tanα随着自变量α的增大而增大
cosα、cotα随着自变量α的增大而减小
问题3:tanα与cotα有怎样的关系? tanα?cotα =1 问题4:当两角互余时,这两角的正弦和余 弦有怎样的关系?正切和余切呢?
sinα= cos(90°-α)
cosα= sin(90°-α)
tanα= cot(90°-α)
cotα= tan(90°-α) 挑战自我 1、求下列各直角三角形中字母的值. 2、如图,在直角坐标平面中,P是第一象限的点,其坐标是(3,y),且OP与x轴的正半轴的夹角a的正切值是 ,求: ?
(1) y的值; (2) 角a的正弦值. ?
(1)y=4(2)sina=情景再现
工程部为测量某建筑物的高度,在离该建筑底部30.0米处,目测其顶,视线与水平线的夹角为40°,目高1.5米.你能帮工程师求出该建筑的高度吗?(精确到0.1米)
∵tan∠AHQ= ∴AQ=HQ?tan∠AHQ
=30.0×tan40°
归纳小结
这堂课我们主要学到了什么?
1、锐角∠A的正弦、余弦、正切、余切函数,统称为 锐角∠A的三角函数。
2、30°、45°、60°角的三角函数值。
3、锐角α的三角函数值的取值范围 。4、三角函数的增减性:正弦 0< sinα<1 正切 tanα>0
余弦 0< cosα<1 余切 cotα>0
sinα、tanα随着自变量α的增大而增大
cosα、cotα随着自变量α的增大而减小
5、相关结论 tanα?cotα =1
sinα= cos(90°-α)
cosα= sin(90°-α)
tanα= cot(90°-α)
cotα= tan(90°-α)
作业
同步练习再见
锐角的三角函数值 工程部为测量某建筑物的高度,在离该建筑底部30.0米处,目测其顶,视线与水平线的夹角为40°,目高1.5米.你能帮工程师求出该建筑的高度吗?(精确到0.1米)直角三角形中边角的再认识如图,Rt△ABC中: 找一找
如图,在Rt△MNP中,∠N=90°.
∠P的对边是_________,∠P的邻边是_______;
∠M的对边是________ ,∠M的邻边是_______;MNPNPNMN如图中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3,
∵ Rt△AB1C1∽Rt△_______∽Rt△________
∴ = =AB3C3AB2C2探索一思考:
在Rt△ABC中,对于锐角A的每一个确定的值,
①∠A的对边与斜边的比值与△ABC的边长大小有关系吗? ②∠A的邻边与斜边的比值呢?
③∠A的对边与邻边的比值呢?
④∠A的邻边与对边的比值呢?
由此可见:
在Rt△ABC中,对于锐角A的每一个确定的值,其对边与斜边、邻边与斜边、对边与邻边、邻边与对边的比值是惟一确定的.
在一个变化过程中,有两个变量X和Y,对于X的每一个值,Y都有惟一的值与之对应,我们就说X是自变量,Y是因变量,此时也称Y是X的函数。????????? 这几个比值都是锐角∠A的函数,记作
sinA、cosA、tanA、cotA,即
sinA = cosA = tanA = cotA = 锐角∠A的正弦、余弦、正切、余切函数,统称为锐角∠A的三角函数.
概括正弦余弦正切余切例 求出如图所示的Rt△ABC中∠A的四个三角函数值. 解:∵ ∴ sinA = cosA = tanA = cotA = 17 求出如图所示的Rt△DEC(∠E=90°)中∠D的四个三角函数值.
牛刀小试 解: ∵ ∴ sinD=
cosD= tanD= cotD= 8探索二(1)根据三角函数的定义,sin30°是一个常数.用刻度尺量出你所用的含30°的三角尺中,30°所对的直角边与斜边的长,与同桌交流,看看这个常数是什么.sin30°=
即斜边等于对边的2倍. 因此我们还可以得到:
在直角三角形中,如果一个锐角等于30°,
那么它所对的直角边等于斜边的一半.
∴ BC= ∵ ∠C=90 °, ∠A=30 °
AB(直角三角形中30 °角所对的直角边等于斜边的一半 )几何论证 (2)根据sin30°= , 怎样求cos30°、tan30°、cot30°的值呢?
cos30°= tan30°= cot30°= sin60°= cos60°= tan60°= cot60°= (3)== (4)用类似的方法求sin45°、cos45°、tan45°、 cot45°的值,并完成课本P109的表格。 sin45°= cos45°= tan45°=
cot45°= 11(5)根据表格,思考以下问题: 问题1:自变量α的取值范围是____________,各因变量的取值范围呢? ??
0°<α< 90° 正弦 0< sinα<1
余弦 0< cosα<1
正切 tanα>0
余切 cotα>0
问题2:各个函数值随着自变量α的增大而怎样变化? sinα、tanα随着自变量α的增大而增大
cosα、cotα随着自变量α的增大而减小
问题3:tanα与cotα有怎样的关系? tanα?cotα =1 问题4:当两角互余时,这两角的正弦和余 弦有怎样的关系?正切和余切呢?
sinα= cos(90°-α)
cosα= sin(90°-α)
tanα= cot(90°-α)
cotα= tan(90°-α) 挑战自我 1、求下列各直角三角形中字母的值. 2、如图,在直角坐标平面中,P是第一象限的点,其坐标是(3,y),且OP与x轴的正半轴的夹角a的正切值是 ,求: ?
(1) y的值; (2) 角a的正弦值. ?
(1)y=4(2)sina=情景再现
工程部为测量某建筑物的高度,在离该建筑底部30.0米处,目测其顶,视线与水平线的夹角为40°,目高1.5米.你能帮工程师求出该建筑的高度吗?(精确到0.1米)
∵tan∠AHQ= ∴AQ=HQ?tan∠AHQ
=30.0×tan40°
归纳小结
这堂课我们主要学到了什么?
1、锐角∠A的正弦、余弦、正切、余切函数,统称为 锐角∠A的三角函数。
2、30°、45°、60°角的三角函数值。
3、锐角α的三角函数值的取值范围 。4、三角函数的增减性:正弦 0< sinα<1 正切 tanα>0
余弦 0< cosα<1 余切 cotα>0
sinα、tanα随着自变量α的增大而增大
cosα、cotα随着自变量α的增大而减小
5、相关结论 tanα?cotα =1
sinα= cos(90°-α)
cosα= sin(90°-α)
tanα= cot(90°-α)
cotα= tan(90°-α)
作业
同步练习再见
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
