21.5 应用举例(3)坡度、坡角问题 课件
文档属性
| 名称 | 21.5 应用举例(3)坡度、坡角问题 课件 |  | |
| 格式 | rar | ||
| 文件大小 | 32.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-21 20:56:00 | ||
图片预览

文档简介
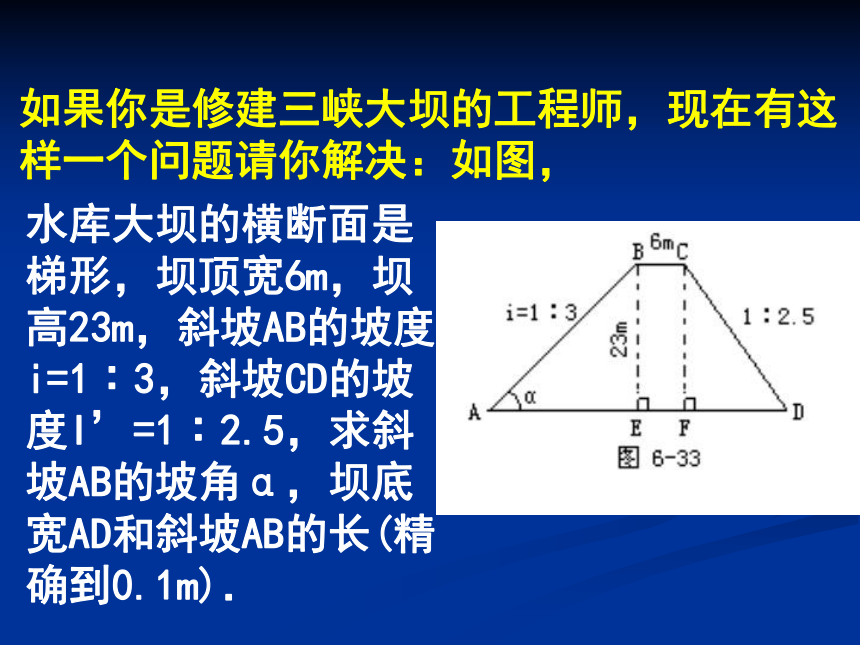
课件9张PPT。应用举例如果你是修建三峡大坝的工程师,现在有这样一个问题请你解决:如图,
水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度I’=1∶2.5,求斜坡AB的坡角α,坝底宽AD和斜坡AB的长(精确到0.1m).
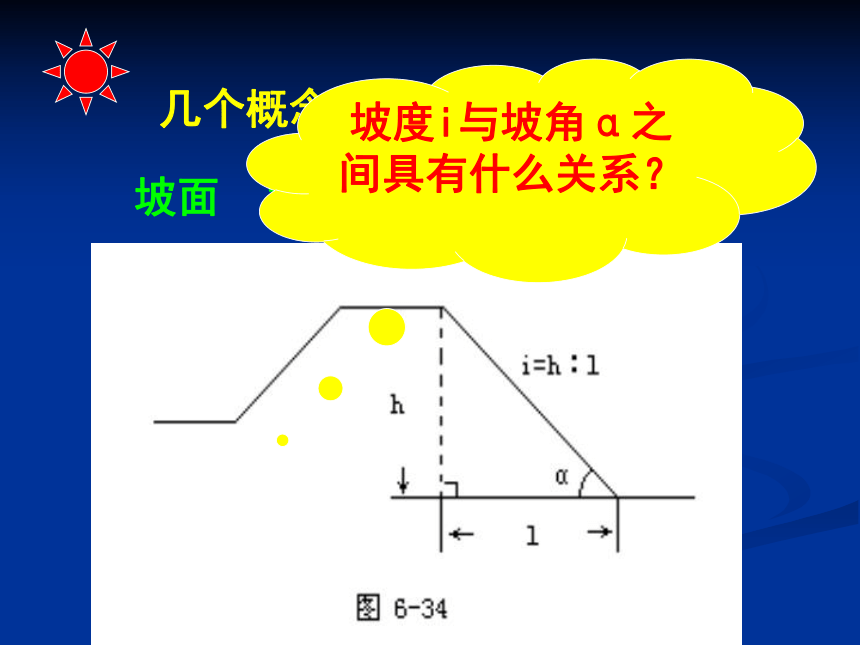
几个概念:坡面 坡度与坡角, 水平距离坡度i与坡角α之间具有什么关系?练习:
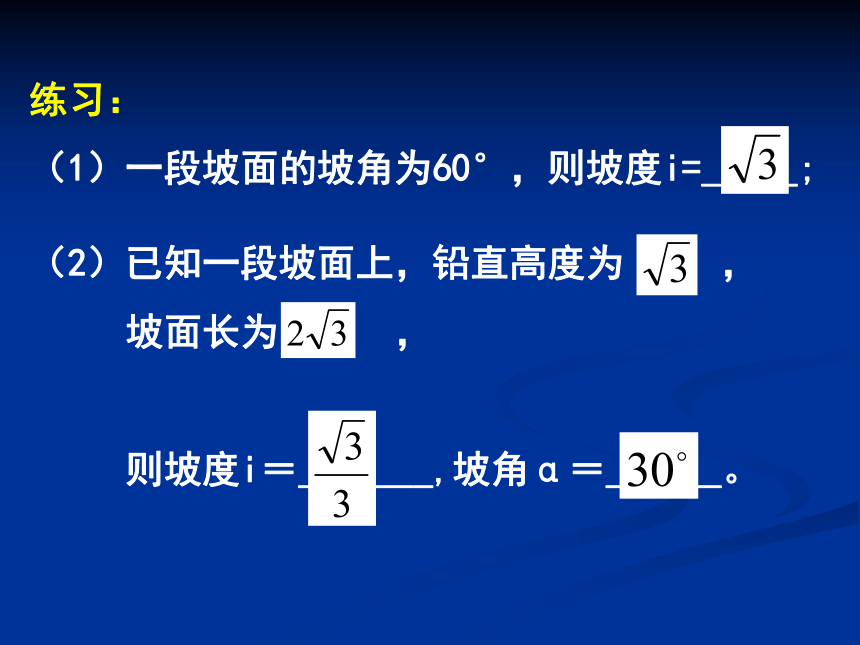
(1)一段坡面的坡角为60°,则坡度i=_____;(2)已知一段坡面上,铅直高度为 ,
坡面长为 ,
则坡度i=_______,坡角α=______。例1:水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i’= 1∶2.5,
求:斜坡AB的坡角α;
坝底宽AD和斜坡AB的长(精确到0.1m).例2:修建一条铁路要经过一座高山,需在山腰B处开凿一条隧道BC。经测量,西山坡的坡度i=5:3,由山顶A观测到点C的俯角为60°,AC的长为60m,如图所示,试求隧道BC的长(结果精确到0.1m)巩固练习: 利用土埂修筑一条渠道,在埂中间挖去深为0.6米的一块(图6-35阴影部分是挖去部分),已知渠道内坡度为1∶1.5,渠道底面宽BC为0.5米,求:
①横断面(等腰梯形)ABCD的面积;
②修一条长为100米的渠道要挖去的土方数. 分析:
1.引导学生将实际问题
转化为数学问题.
2.要求S等腰梯形ABCD,
首先要求 出AD,
如何利用条件求AD?
3.土方数=S·l
∴AE=1.5×0.6=0.9(米).
∵等腰梯形ABCD,
∴FD=AE=0.9(米).
∴AD=2×0.9+0.5=2.3(米).总土方数=截面积×渠长
=0.8×100=80(米3).
答:横断面ABCD面积为0.8平方米,修一条长为100米的渠道要挖出的土方数为80立方米.
课堂小结: 1.弄清俯角、仰角、株距、坡度、坡角、水平距离、垂直距离、水位等概念的意义,明确各术语与示意图中的什么元素对应,只有明确这些概念,才能恰当地把实际问题转化为数学问题. 2.认真分析题意、画图并找出要求的直角三角形,或通过添加辅助线构造直角三角形来解决问题. 3.选择合适的边角关系式,使计算尽可能简单,且不易出错.
4.按照题中的精确度进行计算,并按照题目中要求的精确度确定答案以及注明单位.
水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度I’=1∶2.5,求斜坡AB的坡角α,坝底宽AD和斜坡AB的长(精确到0.1m).
几个概念:坡面 坡度与坡角, 水平距离坡度i与坡角α之间具有什么关系?练习:
(1)一段坡面的坡角为60°,则坡度i=_____;(2)已知一段坡面上,铅直高度为 ,
坡面长为 ,
则坡度i=_______,坡角α=______。例1:水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i’= 1∶2.5,
求:斜坡AB的坡角α;
坝底宽AD和斜坡AB的长(精确到0.1m).例2:修建一条铁路要经过一座高山,需在山腰B处开凿一条隧道BC。经测量,西山坡的坡度i=5:3,由山顶A观测到点C的俯角为60°,AC的长为60m,如图所示,试求隧道BC的长(结果精确到0.1m)巩固练习: 利用土埂修筑一条渠道,在埂中间挖去深为0.6米的一块(图6-35阴影部分是挖去部分),已知渠道内坡度为1∶1.5,渠道底面宽BC为0.5米,求:
①横断面(等腰梯形)ABCD的面积;
②修一条长为100米的渠道要挖去的土方数. 分析:
1.引导学生将实际问题
转化为数学问题.
2.要求S等腰梯形ABCD,
首先要求 出AD,
如何利用条件求AD?
3.土方数=S·l
∴AE=1.5×0.6=0.9(米).
∵等腰梯形ABCD,
∴FD=AE=0.9(米).
∴AD=2×0.9+0.5=2.3(米).总土方数=截面积×渠长
=0.8×100=80(米3).
答:横断面ABCD面积为0.8平方米,修一条长为100米的渠道要挖出的土方数为80立方米.
课堂小结: 1.弄清俯角、仰角、株距、坡度、坡角、水平距离、垂直距离、水位等概念的意义,明确各术语与示意图中的什么元素对应,只有明确这些概念,才能恰当地把实际问题转化为数学问题. 2.认真分析题意、画图并找出要求的直角三角形,或通过添加辅助线构造直角三角形来解决问题. 3.选择合适的边角关系式,使计算尽可能简单,且不易出错.
4.按照题中的精确度进行计算,并按照题目中要求的精确度确定答案以及注明单位.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
