21.5 应用举例（2）航海问题 课件

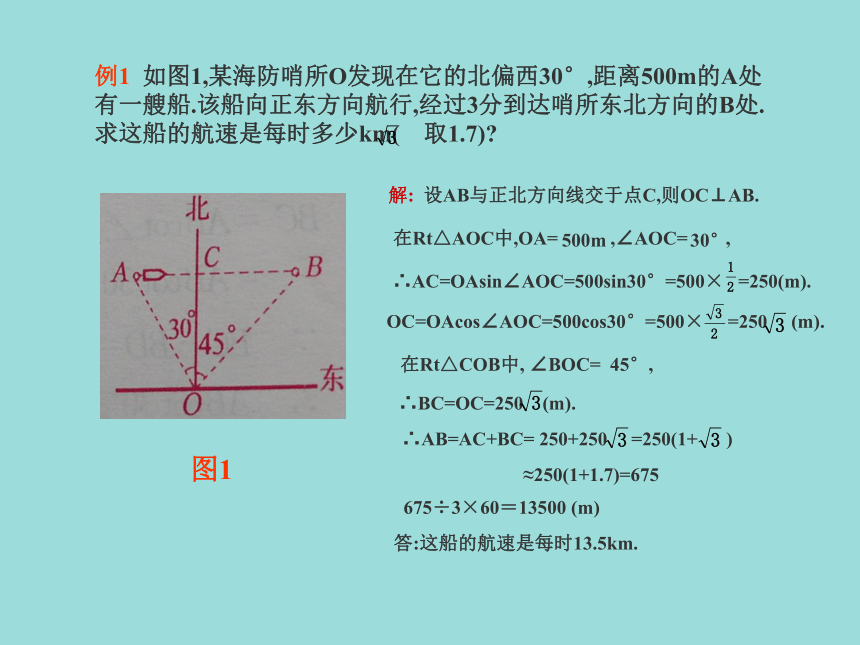
课件9张PPT。解直角三角形应用举例例1 如图1,某海防哨所O发现在它的北偏西30°,距离500m的A处有一艘船.该船向正东方向航行,经过3分到达哨所东北方向的B处.求这船的航速是每时多少km( 取1.7)? 图1解: 设AB与正北方向线交于点C,则OC⊥AB. 在Rt△AOC中,OA= ,∠AOC= ,?500m30°∴AC=OAsin∠AOC=500sin30°=500× =250(m). OC=OAcos∠AOC=500cos30°=500× =250 (m). ∴AB=AC+BC= 250+250 =250(1+ )
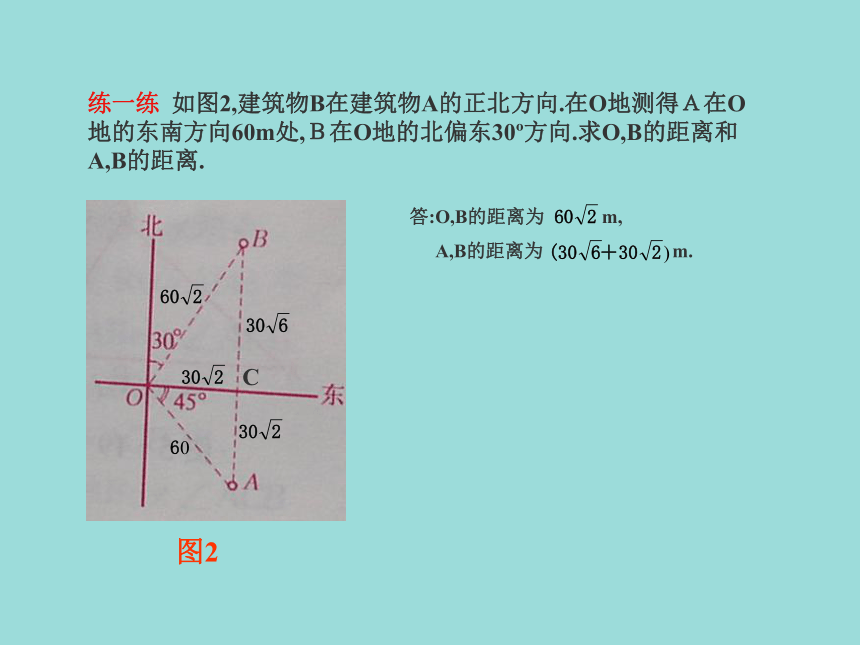
675÷3×60＝13500 (m)答:这船的航速是每时13.5km.≈250(1+1.7)=675练一练 如图2,建筑物B在建筑物A的正北方向.在O地测得Ａ在O地的东南方向60m处,Ｂ在O地的北偏东30o方向.求O,B的距离和A,B的距离.图2C答:O,B的距离为 m,
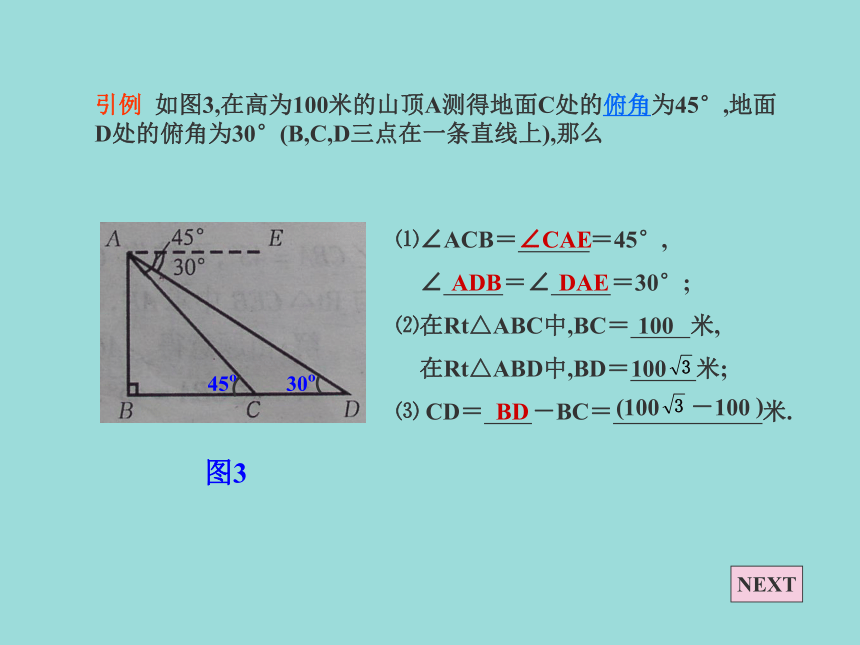
A,B的距离为 m. 引例 如图3,在高为100米的山顶A测得地面C处的俯角为45°,地面D处的俯角为30°(B,C,D三点在一条直线上),那么图3⑴∠ACB＝ ＝45°,
∠ ＝∠ ＝30°;
⑵在Rt△ABC中,BC＝ 米,
在Rt△ABD中,BD＝ 米;
⑶ CD＝ －BC＝ 米.100BD100NEXT仰角、俯角的定义:仰角和俯角:
指视线和水平线所成的角.
⑴仰角:视线在水平线上方时
⑵俯角:视线在水平线下方时BACK例2 如图4,河对岸有水塔AB.在C处测得塔顶A的仰角为30o,向塔前进12m到达D,在D处测得A的仰角为45o,求塔高.解: 在Rt△ADB中,
BD= ABcot∠ADB=ABcot45°. 在Rt△ACB中,
BC= ABcot∠ACB=ABcot30°. ∵ BC －BD=CD,CD = 12m,即 ABcot30o － ABcot45o = 12,∴答:塔高为( )m.想一想 :
还可以怎
么解?
图4评注: 因CD不是可解直角三角形的一边,
这时通常可考虑用线段的和或差这一间接方法.例2 如图4,河对岸有水塔AB.在C处测得塔顶A的仰角为30o,向塔前进12m到达D,在D处测得A的仰角为45o,求塔高.小结:本例告诉我们在应用解直角三角形解决测量问题时,一般要先画
出测量示意图, 然后借助示意图,利用直角三角形中角、边之间的
数量关系求出所要求的距离或角度.图4例3 如图6,公路MN和公路PQ在点P处交汇,且∠QPN=30o,点A处有一所中学,AP=160米,假设拖拉机行驶时,周围100米内会受到噪声的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受到噪声影响?说明理由;如果受影响,已知拖拉机速度为18千米/时,那么学校受到影响的时间为多少秒?B解: 作AB⊥MN于B,
在Rt△ABP中,
∵ ∠ABP=90o, ∠APB=30o,AP=160
∴ AB= ·AP=80
∵点A到直线MN的距离小于100米
∴这所中学会受到噪声的影响.?
. 假设拖拉机在公路MN上沿PN方向行驶到
点C处,学校开始受到噪声影响, 那么
AC＝100(米), 由勾股定理
BC＝ ＝60(米) 同理拖拉机行驶到点D处,学校开始脱离
噪声影响,那么BD＝60米. ∴CD＝120(米)＝0.12千米 ∴学校受噪声影响的时间t＝
1.解直角三角形,就是在直角三角形中,知道除直角外的其他
五个元素中的两个(其中至少有一个是边),求出其它元素的
过程.
2.与之相关的应用题有:求山高或建筑物的高;测量河的宽度
或物体的长度;航行航海问题等.解决这类问题的关键就是
把实际问题转化为数学问题,结合示意图,运用解直角三角
形的知识.
3.当遇到30o,45o,60o等特殊角时,常常添加合适的辅助线分割
出包含这些角度的直角三角形来解决某些斜三角形的问题.
4.应用解直角三角形知识解应用题时,可按以下思维过程进行:
⑴寻找直角三角形,若找不到,可构造;
⑵找到的直角三角形是否可解,若不可直接求解,利用题中
的数量关系,设x求解.【课堂点睛】 :