人教版八年级数学上册 第十三章《轴对称》单元测试卷(含解析)
文档属性
| 名称 | 人教版八年级数学上册 第十三章《轴对称》单元测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-19 11:27:16 | ||
图片预览

文档简介
第十三章《轴对称》单元测试卷
一、单选题(本大题共10小题,每小题3分,共30分)
1.下列图形是轴对称图形的是( )
A. B. C. D.
2.如图,射线与射线平行,点F为射线上的一定点,作直线,点P是射线上的一个动点(不包括端点C),将沿折叠,使点C落在点E处.若,当点E到点A的距离最大时,的度数为( )
A. B. C. D.
3.如图,在3×3的正方形网格中,点A、B在格点(网格线的交点)上,要找一个格点C,连接AC,BC,使ABC成为轴对称图形,则符合条件的格点C的个数是( )
A.5个 B.4个 C.3个 D.2个
4.如图,,和分别平分和,过点P且与垂直,若,,则的面积为( )
A.15 B.20 C.30 D.80
5.如图,,C为OB上的定点,M,N分别为射线OA、OB上的动点.当的值最小时,的度数为( )
A. B. C. D.
6.将长为2、宽为a(a大于1且小于2)的长方形纸片按如图①所示的方式折叠并压平,剪下一个边长等于长方形宽的正方形,称为第一次操作;再把剩下的长方形按如图②所示的方式折叠并压平,剪下个边长等于此时长方形宽的正方形,称为第二次操作;如此反复操作下去…,若在第n次操作后,剩下的长方形恰为正方形,则操作终止.当n=3时,a的值为( )
A.1.8或1.5 B.1.5或1.2 C.1.5 D.1.2
7.如图,AD是△ABC 的角平分线,DF⊥AB,垂足为F,且DE=DG,则∠AED+∠AGD和是( )
A.180° B.200° C.210° D.240°
8.如图,在中,,若D是边上的动点,则的最小值是( )
A.6 B.8 C.10 D.12
9.如图,中,,,.则为( )
A. B. C. D.
10.如图,在中,和的平分线相交于点,过点作直线交于点,交于点,过点作于,有下列四个结论:①;②;③点到各边的距离相等;④设,,则,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共8小题,每小题4分,共32分)
11.平面上的两条相交直线是轴对称图形,它有 条对称轴.
12.如图,的外角的平分线与内角的平分线交于点,若,则 .
13.如图,长方形纸片中,,,且,将长方形纸片沿直线翻折,使点C落在边上,记作点N,再将沿直线向左翻折,使点D落在射线上,记作点P,若点N,P,A三点中有一点是另外两点的中点,则的值为 .
14.如图,在中,.P是边上一点,,连接,以为边在的右上方作等边三角形.若,则点Q到边的距离为
15.如图,在中,D为中点,,,于点F,,,则的长为 .
16.在中,,平分,过A作的垂线交直线于点M,若,则的度数为 .
17.如图,边长为a的等边中,BF是AC上的中线且,点D在BF上,连接AD,在AD的右侧作等边,连接EF,则周长的最小值是 ,此时 .
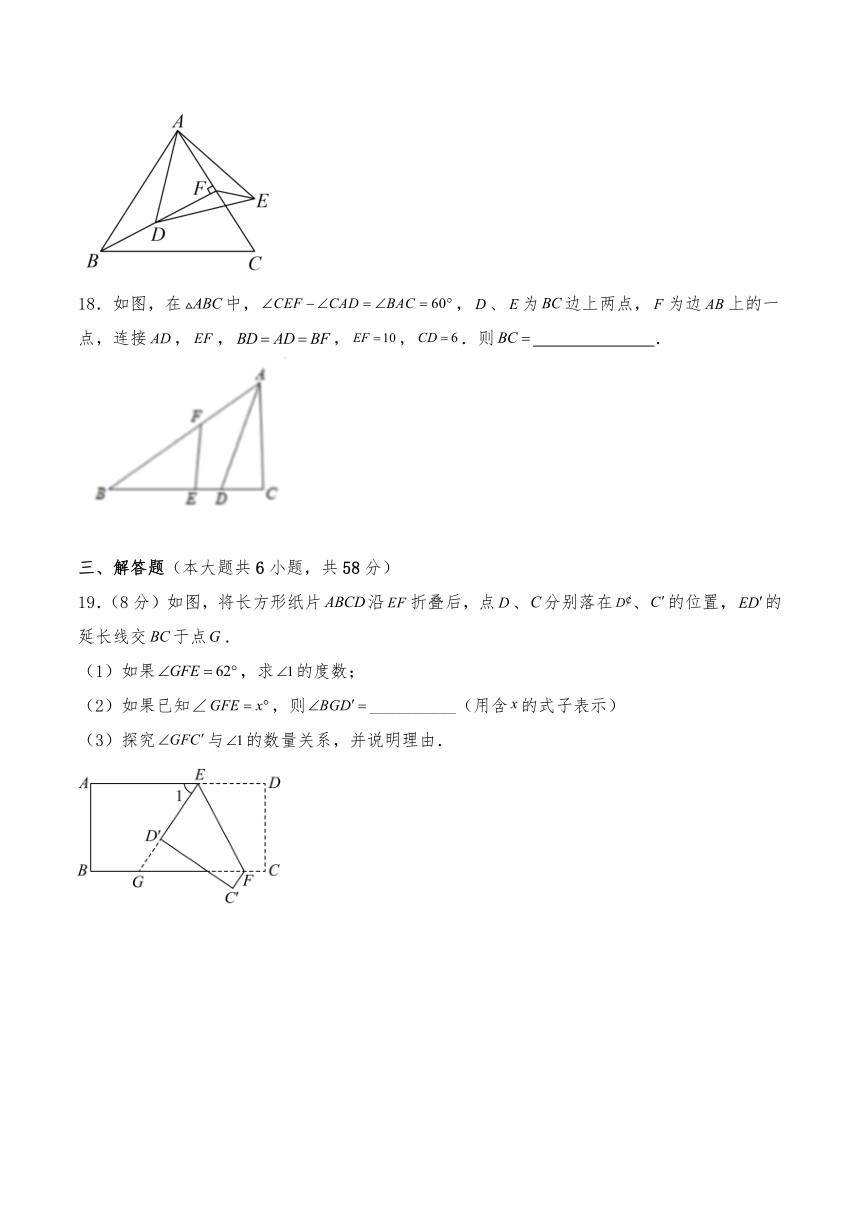
18.如图,在中,,、为边上两点,为边上的一点,连接,,,,.则 .
三、解答题(本大题共6小题,共58分)
19.(8分)如图,将长方形纸片沿折叠后,点、分别落在、的位置,的延长线交于点.
(1)如果,求的度数;
(2)如果已知∠,则__________(用含的式子表示)
(3)探究与的数量关系,并说明理由.
20.(8分)如图,在和中,,,,与交于点(不与点,重合),点,在异侧,,的平分线相交于点.
(1)当时,求的长;
(2)求证:;
(3)当时,求的取值范围.
21.(10分)如图,在中,为边上的高,是的角平分线,点F为上一点,连接,.
(1)求证:平分;
(2)连接交于点G,若,求证:;
(3)在(2)的条件下,当,时,求线段的长.
22.(10分)如图,已知∠ABC=∠ADC=90°,BC=CD,CA=CE.
(1)求证:∠ACB=∠ACD;
(2)过点E作ME∥AB,交AC的延长线于点M,过点M作MP⊥DC,交DC的延长线于点P.
①连接PE,交AM于点N,证明AM垂直平分PE;
②点O是直线AE上的动点,当MO+PO的值最小时,证明点O与点E重合.
23.(10分)如图①,在中,,,直线过点,且,点是直线上一点,不与点重合
(1)若点是图①中线段上一点,且,请判断线段与的位置关系,并说明理由;
(2)如图②,在(1)的条件下,连接,过点作交线段于点,求证:;
(3)如图③,在图①的基础上,改变点的位置后,连接,过点作交线段的延长线于点,请判断线段与的数量关系,并说明理由
24.(12分)已知,为等边三角形,点D在边上.
【基本图形】如图1,以为一边作等边三角形,连接.请直接写出之间的关系.
【迁移运用】如图2,点F是边上一点,以为一边作等边三角.求证:.
【类比探究】如图3,点F是边的延长线上一点,以为一边作等边三角形.试探究线段三条线段之间存在怎样的数量关系,请写出你的结论并说明理由.
答案
一、单选题
1.C
【分析】根据轴对称图形的定义判断即可.
【详解】∵ 不是轴对称图形,
∴A不符合题意;
∵ 不是轴对称图形,
∴B不符合题意;
∵ 是轴对称图形,
∴C符合题意;
∵ 不是轴对称图形,
∴D不符合题意;
故选C.
2.B
【分析】由平行线的性质得,由,当点E在上时,点E到点A的距离最大,然后可求出的度数.
解:∵,,
∴,
∵,
∴当点E在上时,点E到点A的距离最大,如图,
由折叠可知,,
∴,
故选B.
3.B
【分析】画出△ABC为轴对称图形时C点位置,解答即可.
解:C点落在网格中的4个格点使△ABC为轴对称图形,
故选:B.
【点拨】本题考查了轴对称图形,解题的关键是熟练掌握轴对称图形的性质.
4.A
【分析】过点P作于点E,根据平行线的性质证,再根据角平分线的性质得出,再根据三角形面积公式计算即可.
解:过点P作于点E,
∵,
∴,
∵,
∴,
∴,即,
∵,和分别平分和,
∴,,
∴,
∵,
∴,
∵,
∴,
故选:A.
5.B
【分析】作点C关于OA的对称点E,作EN⊥OC交OA于点M,此时CM+MN=EM+MN=EN最短,进而根据∠AOB=35°,和直角三角形两个锐角互余即可求解.
解:如图:
作点C关于OA的对称点E,过点E作EN⊥OC于点N,交OA于点M,
∴ME=MC,
∴CM+MN=EM+MN=EN,
根据垂线段最短,
EN最短,
∵∠AOB=35°,
∠ENO=CFM=90°,
∴∠OMN=55°,∠OCF=55°,
∴∠EMF=∠OMN=55°,
∴∠E=∠MCE=35°,
∴∠OCM=∠OCF -∠MCE=20°.
故选:B.
6.B
【分析】经过第一次操作可知剩下的长方形一边长为a,另一边长为2﹣a;若第二次操作后,剩下的长方形恰好是正方形,则所以剩下的长方形的两边分别为2﹣a、a﹣(2﹣a)=2a﹣2;根据第2次剩下的长方形分两种情况讨论,若第三次操作后,剩下的长方形恰好是正方形,由此可得出关于a的一元一次方程,解之即可得出结论.
解:第1次操作,剪下的正方形边长为a,剩下的长方形的长宽分别为a、2﹣a,由1<a<2,得a>2﹣a;第2次操作,剪下的正方形边长为2﹣a,所以剩下的长方形的两边分别为2﹣a、a﹣(2﹣a)=2a﹣2,
①当2a﹣2<2﹣a,即a<时,
则第3次操作时,剪下的正方形边长为2a﹣2,剩下的长方形的两边分别为2a﹣2、(2﹣a)﹣(2a﹣2)=4﹣3a,则2a﹣2=4﹣3a,解得a=1.2;
②2a﹣2>2﹣a,即a>时
则第3次操作时,剪下的正方形边长为2﹣a,剩下的长方形的两边分别为2﹣a、(2a﹣2)﹣(2﹣a)=3a﹣4,则2﹣a=3a﹣4,解得a=1.5.
故选:B.
7.A
【分析】过点作于,如图,根据角平分线的性质得到,则可根据“”判断,所以,然后利用得到.
解:过点作于,如图,
是的角平分线,,,
,
在和中,
,
,
,
,
.
故选:A.
8.D
【分析】过点C作射线,使,再过动点D作,垂足为点F,连接,在中,当A,D,F在同一直线上,即时,的值最小,最小值等于垂线段的长.
解:过点C作射线,使,再过动点D作,垂足为点F,连接,如图所示:
在中,,
∴,
∵
=,
∴当A,D,F在同一直线上,即时,的值最小,最小值等于垂线段的长,
此时,,
∴是等边三角形,
∴,
在中,,
∴,
∴,
∴,
∴,
∴,
∴的最小值为12,
故选:D.
9.B
【分析】可过C作于E,因为,则可得,可过C作于E,依据题意可得,进而得到,得到,再利用等腰三角形的判定可得,即可求得.
【详解】如图,可过C作于E,可过C作于E.
∵,
∴,
∴,
∵,,
∴,
∴,,且
∴,
∴,且
∴,且,
∴,
∴,
∴
∴
故选:B.
10.C
【分析】根据三角形的内角和与角平分线的性质可得,可判断①和②;过点作于点,过点作于点,连接,根据角平分线的性质可知,可判断③;将的面积转化成的面积与的面积之和,可判断④.
解:在中,,
∵,
∴,
∵和的平分线相交于点,
∴,,
∴,
∴,
∴结论①不正确,结论②正确;
过点作于点,过点作于点,连接,
∵平分,OC平分,
∴,
又∵,
∴,
∴,
∴结论③正确,
∵,,
∴,
设,,
∴,
∴结论④正确,
∴正确的结论有:②③④,
故选:C.
二、填空题
11.2
【分析】根据轴对称的性质即可解答.
【详解】平面内两条相交的两直线是轴对称图形,两对对顶角的角平分线所在的直线是这个图形的两条对称轴.
故答案为2.
12.
【分析】延长,作,,,设,,进而根据三角形的外角的性质得出,证明,即可求解.
【详解】延长,作,,,
设,
平分,
,,
平分,
,,
,
,
,
,
,
在和中,
,
,
.
故答案为:.
13.3或
【分析】分两种情况讨论,利用折叠的性质和矩形的性质可求解.
解:∵将长方形纸片沿直线翻折,
∴,
将沿直线向左起折,当点D落在线段上时,如图,
∴,
∵点P是的中点,
∴,
∴,
∴;
当点D落在线段的延长线上时,如图,
∴,
∵点A是的中点,
∴,
∴,
∴,
故答案为:3或.
14.
【分析】如图,过作于,则,,则,由等边三角形,可得,,,证明,根据,求解即可.
解:如图,过作于,则,
∵,
∴,
∴,
∵等边三角形,
∴,,
∴,即,
∵,,,
∴,
∴,
故答案为:.
15.
【分析】连接,过点E作,交的延长线于N,由,可得;由D为中点,,则可得;证明,再证明即可求得结果.
解:连接,过点E作,交的延长线于N,如图,
∵,,
∴;
∵D为中点,,
∴;
∵,,
∴,
∵,
∴,
∴;
∵,,,
∴,
∴,
∴,
即,
∴.
故答案为:.
16.或
【分析】分两种情况讨论:当点M在延长线上时,当点M在延长线上时,分别画出图形,作出辅助线,求出结果即可.
解:当点M在延长线上时,延长,在的延长线上截取,连接,如图所示:
∵,,
∴,
∴,
∵,平分,
∴,
∵,
∴,
∴,
∵,
∴,
∵,,
∴,
∴,
设,则,
∵,
∴,
解得:,
即;
当点M在延长线上时,延长,在的延长线上截取,连接,如图所示:
∵,,
∴,
∴,
∵,平分,
∴,
∵,
∴,
∴,
∵,
∴,
∵,,
∴,
∴,
设,则,,
∵,
∴,
解得:,
即;
故答案为:或.
17. /90度
【分析】通过分析点E的运动轨迹,点E在射线上运动(),作点A关于直线的对称点M,连接交于点,此时的值最小
解:∵,均为等边三角形,
∴,
∴,
∴,
∴,
∴,
∴
∴点E在射线上运动()
作点A关于直线的对称点M,连接交于点,此时的值最小,
∵
∴是等边三角形,
∴,
∵,
∴,
∴周长的最小值是,
故答案为:,
18.22
【分析】如图,在右侧作,交延长线于点K,过点D作,交于G,交于L,过L分别作、、的高,分别相交于H、I、J;由根据平行线和角的数量关系得到,,从而得到,将转到,利用角的关系和角平分线的性质可再证明,然后利用线段的关系计算从而得出结果.
【详解】如图,在右侧作,交延长线于点K,过点D作,交于G,交于L,过L分别作、、的高,分别相交于H、I、J;
,
,
是的平分线;
又
在与中,
;
又角平分线、交于L,
,,
在与中,
,
在与中,
,,
.
故答案为22.
三、解答题
19.(1)解:,
,
由折叠知,
,
;
(2),
,
由折叠的性质可得:,
;
(3),
,
,
,
.
20.(1)∵,
∴为直角三角形,,
∵,
∴;
∴;
(2)在和中,
∵
∴,
∴,
∵,
∴;
(3)∵
∴
设,则,
∵,
∴,
∵分别平分,
∴,,
∴
=
=,
∵,
∴.
21.(1)证明: 是的角平分线,
.
,
.
.
为边上的高,
.
.
平分.
(2)过点F作于点M,于点N,
平分,且,,
.
,
,
平分,
,
在和 CBF中,
,
,
,
,
,
(3),
,,
,
为边上的高,
,
,
.
在和中,
.
,
,
,
,
.
22.(1)证明:在Rt△ABC和Rt△ADC中,
BC=CD,AC=AC,
∴Rt△ABC≌Rt△ADC,
∴∠ACB=∠ACD;
(2)∵Rt△ABC≌Rt△ADC,
∴∠BAC=∠CAD,
∵CA=CE,
∴∠CAE=∠CED,
∵∠EBA=90°,
∴∠BEA=∠BAC=∠CAE=30°,
∵PD⊥AE,MP⊥PD,
∴AE∥MP,
∴∠PMC=∠MAE=30°,
∵ME∥AB,
∴∠MEB=90°,
∴∠MEA=120°,
∵∠MAE=30°,
∴∠EMA=30°,
∵CP⊥MP,CE⊥ME,
∴∠MCP=∠MCE=60°,
∴△NEC≌△NPC (SAS),
∴EN=PN,
∴ N是EP的中点,NC⊥PE,
∴AM垂直平分PE;
②作P点关于AE的对称点,连接M交AE于点O,
∵AM垂直平分PE,
∴ME=MP,
∵∠EMP=60°,
∴∠MPE=60°,
∴∠EPD=30°,
∴∠=30°,
∴∠ MP=30°,
∵∠MEP=60°,
∴O点与E点重合.
23.(1)解:.
证明:在中,,,
,
,
,
,
,
,
;
(2),
,
,
,,
,
是 ADE的外角,
,
,
,
在和中,
;
(3)如图:过点作交线段的延长线于点,
∴∠ADF=900,
,
,,
,
,
,
,
,
,
,
在和中,
,
.
24.
解:基本图形:
∵是等边三角形,等边三角形 ADE,
∴,
∴,
在与 CAE中
,
∴,
∴
∴,即;
迁移运用:
证明:过点作,交于点,
∵是等边三角形,
∴,
∵,
∴,,
又∵,
∴为等边三角形,
∴,
∵为等边三角形,
∴,,
∵,,
∴,
在与中
,
∴,
∴,
∴;
类比探究:
解:,理由如下:
过点作,交于点,
∵是等边三角形,
∴,
∵,
∴,,
又∵,
∴为等边三角形,
∴,
∵为等边三角形,
∴,,
∵,,
∴,
在与中
,
∴,
∴,
∵,
∴.
一、单选题(本大题共10小题,每小题3分,共30分)
1.下列图形是轴对称图形的是( )
A. B. C. D.
2.如图,射线与射线平行,点F为射线上的一定点,作直线,点P是射线上的一个动点(不包括端点C),将沿折叠,使点C落在点E处.若,当点E到点A的距离最大时,的度数为( )
A. B. C. D.
3.如图,在3×3的正方形网格中,点A、B在格点(网格线的交点)上,要找一个格点C,连接AC,BC,使ABC成为轴对称图形,则符合条件的格点C的个数是( )
A.5个 B.4个 C.3个 D.2个
4.如图,,和分别平分和,过点P且与垂直,若,,则的面积为( )
A.15 B.20 C.30 D.80
5.如图,,C为OB上的定点,M,N分别为射线OA、OB上的动点.当的值最小时,的度数为( )
A. B. C. D.
6.将长为2、宽为a(a大于1且小于2)的长方形纸片按如图①所示的方式折叠并压平,剪下一个边长等于长方形宽的正方形,称为第一次操作;再把剩下的长方形按如图②所示的方式折叠并压平,剪下个边长等于此时长方形宽的正方形,称为第二次操作;如此反复操作下去…,若在第n次操作后,剩下的长方形恰为正方形,则操作终止.当n=3时,a的值为( )
A.1.8或1.5 B.1.5或1.2 C.1.5 D.1.2
7.如图,AD是△ABC 的角平分线,DF⊥AB,垂足为F,且DE=DG,则∠AED+∠AGD和是( )
A.180° B.200° C.210° D.240°
8.如图,在中,,若D是边上的动点,则的最小值是( )
A.6 B.8 C.10 D.12
9.如图,中,,,.则为( )
A. B. C. D.
10.如图,在中,和的平分线相交于点,过点作直线交于点,交于点,过点作于,有下列四个结论:①;②;③点到各边的距离相等;④设,,则,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共8小题,每小题4分,共32分)
11.平面上的两条相交直线是轴对称图形,它有 条对称轴.
12.如图,的外角的平分线与内角的平分线交于点,若,则 .
13.如图,长方形纸片中,,,且,将长方形纸片沿直线翻折,使点C落在边上,记作点N,再将沿直线向左翻折,使点D落在射线上,记作点P,若点N,P,A三点中有一点是另外两点的中点,则的值为 .
14.如图,在中,.P是边上一点,,连接,以为边在的右上方作等边三角形.若,则点Q到边的距离为
15.如图,在中,D为中点,,,于点F,,,则的长为 .
16.在中,,平分,过A作的垂线交直线于点M,若,则的度数为 .
17.如图,边长为a的等边中,BF是AC上的中线且,点D在BF上,连接AD,在AD的右侧作等边,连接EF,则周长的最小值是 ,此时 .
18.如图,在中,,、为边上两点,为边上的一点,连接,,,,.则 .
三、解答题(本大题共6小题,共58分)
19.(8分)如图,将长方形纸片沿折叠后,点、分别落在、的位置,的延长线交于点.
(1)如果,求的度数;
(2)如果已知∠,则__________(用含的式子表示)
(3)探究与的数量关系,并说明理由.
20.(8分)如图,在和中,,,,与交于点(不与点,重合),点,在异侧,,的平分线相交于点.
(1)当时,求的长;
(2)求证:;
(3)当时,求的取值范围.
21.(10分)如图,在中,为边上的高,是的角平分线,点F为上一点,连接,.
(1)求证:平分;
(2)连接交于点G,若,求证:;
(3)在(2)的条件下,当,时,求线段的长.
22.(10分)如图,已知∠ABC=∠ADC=90°,BC=CD,CA=CE.
(1)求证:∠ACB=∠ACD;
(2)过点E作ME∥AB,交AC的延长线于点M,过点M作MP⊥DC,交DC的延长线于点P.
①连接PE,交AM于点N,证明AM垂直平分PE;
②点O是直线AE上的动点,当MO+PO的值最小时,证明点O与点E重合.
23.(10分)如图①,在中,,,直线过点,且,点是直线上一点,不与点重合
(1)若点是图①中线段上一点,且,请判断线段与的位置关系,并说明理由;
(2)如图②,在(1)的条件下,连接,过点作交线段于点,求证:;
(3)如图③,在图①的基础上,改变点的位置后,连接,过点作交线段的延长线于点,请判断线段与的数量关系,并说明理由
24.(12分)已知,为等边三角形,点D在边上.
【基本图形】如图1,以为一边作等边三角形,连接.请直接写出之间的关系.
【迁移运用】如图2,点F是边上一点,以为一边作等边三角.求证:.
【类比探究】如图3,点F是边的延长线上一点,以为一边作等边三角形.试探究线段三条线段之间存在怎样的数量关系,请写出你的结论并说明理由.
答案
一、单选题
1.C
【分析】根据轴对称图形的定义判断即可.
【详解】∵ 不是轴对称图形,
∴A不符合题意;
∵ 不是轴对称图形,
∴B不符合题意;
∵ 是轴对称图形,
∴C符合题意;
∵ 不是轴对称图形,
∴D不符合题意;
故选C.
2.B
【分析】由平行线的性质得,由,当点E在上时,点E到点A的距离最大,然后可求出的度数.
解:∵,,
∴,
∵,
∴当点E在上时,点E到点A的距离最大,如图,
由折叠可知,,
∴,
故选B.
3.B
【分析】画出△ABC为轴对称图形时C点位置,解答即可.
解:C点落在网格中的4个格点使△ABC为轴对称图形,
故选:B.
【点拨】本题考查了轴对称图形,解题的关键是熟练掌握轴对称图形的性质.
4.A
【分析】过点P作于点E,根据平行线的性质证,再根据角平分线的性质得出,再根据三角形面积公式计算即可.
解:过点P作于点E,
∵,
∴,
∵,
∴,
∴,即,
∵,和分别平分和,
∴,,
∴,
∵,
∴,
∵,
∴,
故选:A.
5.B
【分析】作点C关于OA的对称点E,作EN⊥OC交OA于点M,此时CM+MN=EM+MN=EN最短,进而根据∠AOB=35°,和直角三角形两个锐角互余即可求解.
解:如图:
作点C关于OA的对称点E,过点E作EN⊥OC于点N,交OA于点M,
∴ME=MC,
∴CM+MN=EM+MN=EN,
根据垂线段最短,
EN最短,
∵∠AOB=35°,
∠ENO=CFM=90°,
∴∠OMN=55°,∠OCF=55°,
∴∠EMF=∠OMN=55°,
∴∠E=∠MCE=35°,
∴∠OCM=∠OCF -∠MCE=20°.
故选:B.
6.B
【分析】经过第一次操作可知剩下的长方形一边长为a,另一边长为2﹣a;若第二次操作后,剩下的长方形恰好是正方形,则所以剩下的长方形的两边分别为2﹣a、a﹣(2﹣a)=2a﹣2;根据第2次剩下的长方形分两种情况讨论,若第三次操作后,剩下的长方形恰好是正方形,由此可得出关于a的一元一次方程,解之即可得出结论.
解:第1次操作,剪下的正方形边长为a,剩下的长方形的长宽分别为a、2﹣a,由1<a<2,得a>2﹣a;第2次操作,剪下的正方形边长为2﹣a,所以剩下的长方形的两边分别为2﹣a、a﹣(2﹣a)=2a﹣2,
①当2a﹣2<2﹣a,即a<时,
则第3次操作时,剪下的正方形边长为2a﹣2,剩下的长方形的两边分别为2a﹣2、(2﹣a)﹣(2a﹣2)=4﹣3a,则2a﹣2=4﹣3a,解得a=1.2;
②2a﹣2>2﹣a,即a>时
则第3次操作时,剪下的正方形边长为2﹣a,剩下的长方形的两边分别为2﹣a、(2a﹣2)﹣(2﹣a)=3a﹣4,则2﹣a=3a﹣4,解得a=1.5.
故选:B.
7.A
【分析】过点作于,如图,根据角平分线的性质得到,则可根据“”判断,所以,然后利用得到.
解:过点作于,如图,
是的角平分线,,,
,
在和中,
,
,
,
,
.
故选:A.
8.D
【分析】过点C作射线,使,再过动点D作,垂足为点F,连接,在中,当A,D,F在同一直线上,即时,的值最小,最小值等于垂线段的长.
解:过点C作射线,使,再过动点D作,垂足为点F,连接,如图所示:
在中,,
∴,
∵
=,
∴当A,D,F在同一直线上,即时,的值最小,最小值等于垂线段的长,
此时,,
∴是等边三角形,
∴,
在中,,
∴,
∴,
∴,
∴,
∴,
∴的最小值为12,
故选:D.
9.B
【分析】可过C作于E,因为,则可得,可过C作于E,依据题意可得,进而得到,得到,再利用等腰三角形的判定可得,即可求得.
【详解】如图,可过C作于E,可过C作于E.
∵,
∴,
∴,
∵,,
∴,
∴,,且
∴,
∴,且
∴,且,
∴,
∴,
∴
∴
故选:B.
10.C
【分析】根据三角形的内角和与角平分线的性质可得,可判断①和②;过点作于点,过点作于点,连接,根据角平分线的性质可知,可判断③;将的面积转化成的面积与的面积之和,可判断④.
解:在中,,
∵,
∴,
∵和的平分线相交于点,
∴,,
∴,
∴,
∴结论①不正确,结论②正确;
过点作于点,过点作于点,连接,
∵平分,OC平分,
∴,
又∵,
∴,
∴,
∴结论③正确,
∵,,
∴,
设,,
∴,
∴结论④正确,
∴正确的结论有:②③④,
故选:C.
二、填空题
11.2
【分析】根据轴对称的性质即可解答.
【详解】平面内两条相交的两直线是轴对称图形,两对对顶角的角平分线所在的直线是这个图形的两条对称轴.
故答案为2.
12.
【分析】延长,作,,,设,,进而根据三角形的外角的性质得出,证明,即可求解.
【详解】延长,作,,,
设,
平分,
,,
平分,
,,
,
,
,
,
,
在和中,
,
,
.
故答案为:.
13.3或
【分析】分两种情况讨论,利用折叠的性质和矩形的性质可求解.
解:∵将长方形纸片沿直线翻折,
∴,
将沿直线向左起折,当点D落在线段上时,如图,
∴,
∵点P是的中点,
∴,
∴,
∴;
当点D落在线段的延长线上时,如图,
∴,
∵点A是的中点,
∴,
∴,
∴,
故答案为:3或.
14.
【分析】如图,过作于,则,,则,由等边三角形,可得,,,证明,根据,求解即可.
解:如图,过作于,则,
∵,
∴,
∴,
∵等边三角形,
∴,,
∴,即,
∵,,,
∴,
∴,
故答案为:.
15.
【分析】连接,过点E作,交的延长线于N,由,可得;由D为中点,,则可得;证明,再证明即可求得结果.
解:连接,过点E作,交的延长线于N,如图,
∵,,
∴;
∵D为中点,,
∴;
∵,,
∴,
∵,
∴,
∴;
∵,,,
∴,
∴,
∴,
即,
∴.
故答案为:.
16.或
【分析】分两种情况讨论:当点M在延长线上时,当点M在延长线上时,分别画出图形,作出辅助线,求出结果即可.
解:当点M在延长线上时,延长,在的延长线上截取,连接,如图所示:
∵,,
∴,
∴,
∵,平分,
∴,
∵,
∴,
∴,
∵,
∴,
∵,,
∴,
∴,
设,则,
∵,
∴,
解得:,
即;
当点M在延长线上时,延长,在的延长线上截取,连接,如图所示:
∵,,
∴,
∴,
∵,平分,
∴,
∵,
∴,
∴,
∵,
∴,
∵,,
∴,
∴,
设,则,,
∵,
∴,
解得:,
即;
故答案为:或.
17. /90度
【分析】通过分析点E的运动轨迹,点E在射线上运动(),作点A关于直线的对称点M,连接交于点,此时的值最小
解:∵,均为等边三角形,
∴,
∴,
∴,
∴,
∴,
∴
∴点E在射线上运动()
作点A关于直线的对称点M,连接交于点,此时的值最小,
∵
∴是等边三角形,
∴,
∵,
∴,
∴周长的最小值是,
故答案为:,
18.22
【分析】如图,在右侧作,交延长线于点K,过点D作,交于G,交于L,过L分别作、、的高,分别相交于H、I、J;由根据平行线和角的数量关系得到,,从而得到,将转到,利用角的关系和角平分线的性质可再证明,然后利用线段的关系计算从而得出结果.
【详解】如图,在右侧作,交延长线于点K,过点D作,交于G,交于L,过L分别作、、的高,分别相交于H、I、J;
,
,
是的平分线;
又
在与中,
;
又角平分线、交于L,
,,
在与中,
,
在与中,
,,
.
故答案为22.
三、解答题
19.(1)解:,
,
由折叠知,
,
;
(2),
,
由折叠的性质可得:,
;
(3),
,
,
,
.
20.(1)∵,
∴为直角三角形,,
∵,
∴;
∴;
(2)在和中,
∵
∴,
∴,
∵,
∴;
(3)∵
∴
设,则,
∵,
∴,
∵分别平分,
∴,,
∴
=
=,
∵,
∴.
21.(1)证明: 是的角平分线,
.
,
.
.
为边上的高,
.
.
平分.
(2)过点F作于点M,于点N,
平分,且,,
.
,
,
平分,
,
在和 CBF中,
,
,
,
,
,
(3),
,,
,
为边上的高,
,
,
.
在和中,
.
,
,
,
,
.
22.(1)证明:在Rt△ABC和Rt△ADC中,
BC=CD,AC=AC,
∴Rt△ABC≌Rt△ADC,
∴∠ACB=∠ACD;
(2)∵Rt△ABC≌Rt△ADC,
∴∠BAC=∠CAD,
∵CA=CE,
∴∠CAE=∠CED,
∵∠EBA=90°,
∴∠BEA=∠BAC=∠CAE=30°,
∵PD⊥AE,MP⊥PD,
∴AE∥MP,
∴∠PMC=∠MAE=30°,
∵ME∥AB,
∴∠MEB=90°,
∴∠MEA=120°,
∵∠MAE=30°,
∴∠EMA=30°,
∵CP⊥MP,CE⊥ME,
∴∠MCP=∠MCE=60°,
∴△NEC≌△NPC (SAS),
∴EN=PN,
∴ N是EP的中点,NC⊥PE,
∴AM垂直平分PE;
②作P点关于AE的对称点,连接M交AE于点O,
∵AM垂直平分PE,
∴ME=MP,
∵∠EMP=60°,
∴∠MPE=60°,
∴∠EPD=30°,
∴∠=30°,
∴∠ MP=30°,
∵∠MEP=60°,
∴O点与E点重合.
23.(1)解:.
证明:在中,,,
,
,
,
,
,
,
;
(2),
,
,
,,
,
是 ADE的外角,
,
,
,
在和中,
;
(3)如图:过点作交线段的延长线于点,
∴∠ADF=900,
,
,,
,
,
,
,
,
,
,
在和中,
,
.
24.
解:基本图形:
∵是等边三角形,等边三角形 ADE,
∴,
∴,
在与 CAE中
,
∴,
∴
∴,即;
迁移运用:
证明:过点作,交于点,
∵是等边三角形,
∴,
∵,
∴,,
又∵,
∴为等边三角形,
∴,
∵为等边三角形,
∴,,
∵,,
∴,
在与中
,
∴,
∴,
∴;
类比探究:
解:,理由如下:
过点作,交于点,
∵是等边三角形,
∴,
∵,
∴,,
又∵,
∴为等边三角形,
∴,
∵为等边三角形,
∴,,
∵,,
∴,
在与中
,
∴,
∴,
∵,
∴.
