19.2平行四边形同步练习(含简单答案)沪科版数学八年级下册
文档属性
| 名称 | 19.2平行四边形同步练习(含简单答案)沪科版数学八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 615.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-19 11:35:37 | ||
图片预览

文档简介
19.2 平行四边形
一、单选题
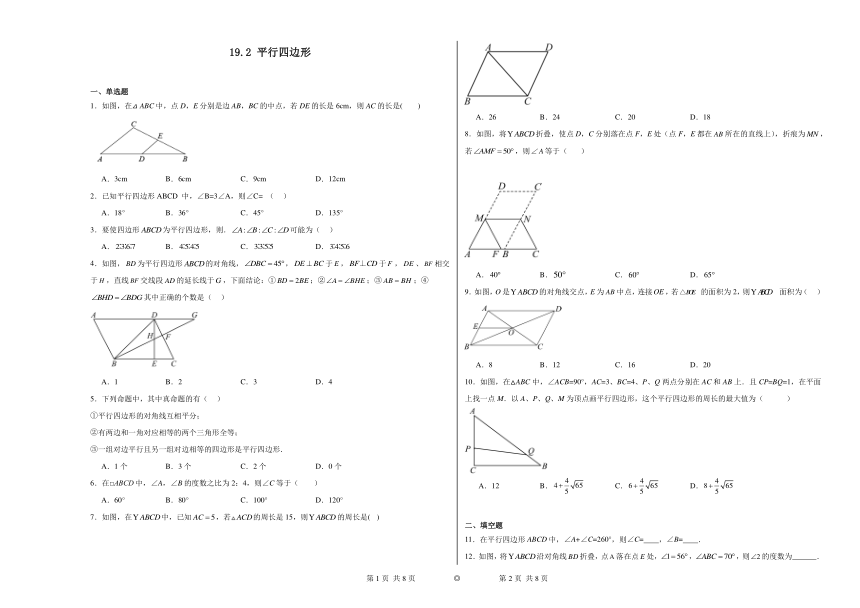
1.如图,在△ABC中,点D,E分别是边AB,BC的中点,若DE的长是6cm,则AC的长是( )
A.3cm B.6cm C.9cm D.12cm
2.已知平行四边形ABCD 中,∠B=3∠A,则∠C= ( )
A.18° B.36° C.45° D.135°
3.要使四边形为平行四边形,则.可能为( )
A. B. C. D.
4.如图,为平行四边形的对角线,,于,于,、相交于,直线交线段的延长线于,下面结论:①;②;③;④其中正确的个数是( )
A.1 B.2 C.3 D.4
5.下列命题中,其中真命题的有( )
①平行四边形的对角线互相平分;
②有两边和一角对应相等的两个三角形全等;
③一组对边平行且另一组对边相等的四边形是平行四边形.
A.1个 B.3个 C.2个 D.0个
6.在□ABCD中,∠A,∠B的度数之比为2:4,则∠C等于( )
A.60° B.80° C.100° D.120°
7.如图,在中,已知,若的周长是15,则的周长是( )
A.26 B.24 C.20 D.18
8.如图,将折叠,使点D,C分别落在点F,E处(点F,E都在所在的直线上),折痕为,若,则等于( )
A. B. C. D.
9.如图,O是的对角线交点,E为中点,连接,若的面积为2,则面积为( )
A.8 B.12 C.16 D.20
10.如图,在△ABC中,∠ACB=90°,AC=3、BC=4、P、Q两点分别在AC和AB上.且CP=BQ=1,在平面上找一点M.以A、P、Q、M为顶点画平行四边形,这个平行四边形的周长的最大值为( )
A.12 B. C. D.
二、填空题
11.在平行四边形ABCD中,∠A+∠C=260°,则∠C= ,∠B= .
12.如图,将沿对角线折叠,点落在点处,,,则的度数为 .
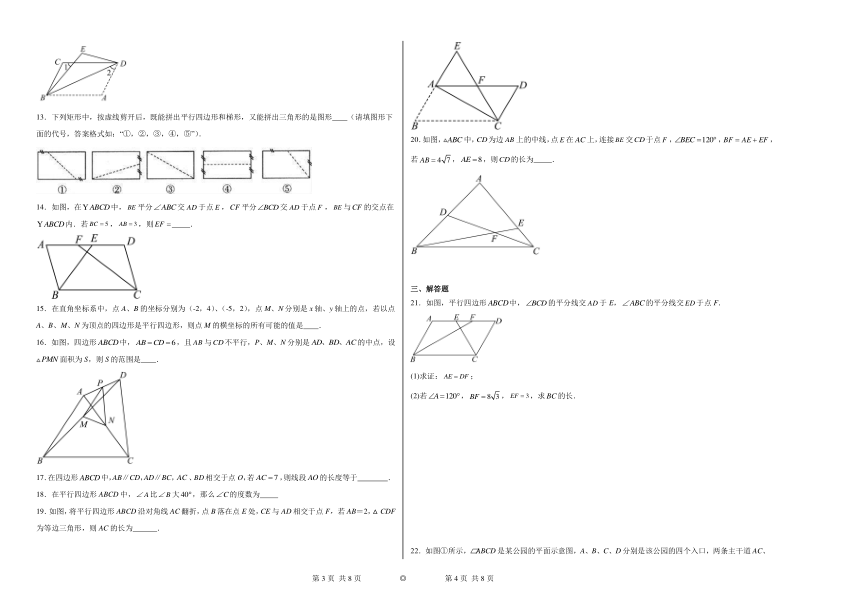
13.下列矩形中,按虚线剪开后,既能拼出平行四边形和梯形,又能拼出三角形的是图形 (请填图形下面的代号,答案格式如:“①,②,③,④,⑤”).
14.如图,在中,平分交于点,平分交于点,与的交点在内.若,,则 .
15.在直角坐标系中,点A、B的坐标分别为(-2,4)、(-5,2),点M、N分别是x轴、y轴上的点,若以点A、B、M、N为顶点的四边形是平行四边形,则点M的横坐标的所有可能的值是 .
16.如图,四边形中,,且与不平行,P、M、N分别是的中点,设面积为S,则S的范围是 .
17.在四边形中,AB∥CD,AD∥BC,、相交于点O,若,则线段的长度等于 .
18.在平行四边形ABCD中,比大,那么的度数为
19.如图,将平行四边形ABCD沿对角线AC翻折,点B落在点E处,CE与AD相交于点F,若AB=2,△CDF为等边三角形,则AC的长为 .
20.如图,中,为边上的中线,点在上,连接交于点,,,若,,则的长为 .
三、解答题
21.如图,平行四边形中,的平分线交于E,的平分线交于点F.
(1)求证:;
(2)若,,,求的长.
22.如图①所示, ABCD是某公园的平面示意图,A、B、C、D分别是该公园的四个入口,两条主干道AC、BD交于点O,经测量AB=0.5km,AC=1.2km,BD=1km,请你帮助公园的管理人员解决以下问题:
(1)公园的面积为 km2;
(2)如图②,公园管理人员在参观了武汉东湖绿道后,为提升游客游览的体验感,准备修建三条绿道AN、MN、CM,其中点M在OB上,点N在OD上,且BM=ON(点M与点O、B不重合),并计划在△AON与△COM两块绿地所在区域种植郁金香,求种植郁金香区域的面积;
(3)若修建(2)中的绿道每千米费用为10万元,请你计算该公园修建这三条绿道投入资金的最小值.
23.如图①所示,是某公园的平面示意图,分别是该公园的四个入口,两条主干道交于点,经测量,,,请你帮助公园的管理人员解决以下问题:
(1)公园的面积为 ;
(2)如图②,公园管理人员在参观了武汉东湖绿道后,为提升游客游览的体验感,准备修建三条绿道,其中点在上,点在上,且(点与点不重合),并计划在与两块绿地所在区域种植郁金香,求种植郁金香区域的面积;
(3)若修建(2)中的绿道每千米费用为10万元,请你画出该公园修建这三条绿道投入资金最小值时的图形.
24.如图,A、B两地被建筑物阻隔,为测量A、B两地的距离,连接、,分别取、的中点、.若的长为,求A、B两地的距离.
25.在一次数学探究活动中,小明用两条直线把平行四边形分割成四个部分,使含有一组对顶角的两个图形全等.
(1)请在图中的三个平行四边形中画出满足小明分割方法的直线;
(2)根据小明的分割方法,你认为把平行四边形分割成满足以上全等关系的直线有______组;由上述实验操作过程,你发现小明所画的两条直线的主要特点是______.
(3)拓展延伸:将一张平行四边形的纸片沿过对角线的中点的直线折叠,折痕交边、于点、,点落在点处,点落在点处.设交于点,分别交、于点、.求证:.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.D
2.C
3.B
4.B
5.A
6.A
7.C
8.D
9.C
10.D
11. 130° 50°
12./42度
13.②
14.1
15.-7,-3,3
16.
17.
18.
19.
20.
21.(1)略.
(2)13
22.(1)0.48;(2)0.12km2;(3)(+5)万元.
23.(1)(2)(3)略
24.
25.(1)略,(答案不唯一);
(2)无数,两条直线都经过平行四边形对角线的交点;
(3)略
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,在△ABC中,点D,E分别是边AB,BC的中点,若DE的长是6cm,则AC的长是( )
A.3cm B.6cm C.9cm D.12cm
2.已知平行四边形ABCD 中,∠B=3∠A,则∠C= ( )
A.18° B.36° C.45° D.135°
3.要使四边形为平行四边形,则.可能为( )
A. B. C. D.
4.如图,为平行四边形的对角线,,于,于,、相交于,直线交线段的延长线于,下面结论:①;②;③;④其中正确的个数是( )
A.1 B.2 C.3 D.4
5.下列命题中,其中真命题的有( )
①平行四边形的对角线互相平分;
②有两边和一角对应相等的两个三角形全等;
③一组对边平行且另一组对边相等的四边形是平行四边形.
A.1个 B.3个 C.2个 D.0个
6.在□ABCD中,∠A,∠B的度数之比为2:4,则∠C等于( )
A.60° B.80° C.100° D.120°
7.如图,在中,已知,若的周长是15,则的周长是( )
A.26 B.24 C.20 D.18
8.如图,将折叠,使点D,C分别落在点F,E处(点F,E都在所在的直线上),折痕为,若,则等于( )
A. B. C. D.
9.如图,O是的对角线交点,E为中点,连接,若的面积为2,则面积为( )
A.8 B.12 C.16 D.20
10.如图,在△ABC中,∠ACB=90°,AC=3、BC=4、P、Q两点分别在AC和AB上.且CP=BQ=1,在平面上找一点M.以A、P、Q、M为顶点画平行四边形,这个平行四边形的周长的最大值为( )
A.12 B. C. D.
二、填空题
11.在平行四边形ABCD中,∠A+∠C=260°,则∠C= ,∠B= .
12.如图,将沿对角线折叠,点落在点处,,,则的度数为 .
13.下列矩形中,按虚线剪开后,既能拼出平行四边形和梯形,又能拼出三角形的是图形 (请填图形下面的代号,答案格式如:“①,②,③,④,⑤”).
14.如图,在中,平分交于点,平分交于点,与的交点在内.若,,则 .
15.在直角坐标系中,点A、B的坐标分别为(-2,4)、(-5,2),点M、N分别是x轴、y轴上的点,若以点A、B、M、N为顶点的四边形是平行四边形,则点M的横坐标的所有可能的值是 .
16.如图,四边形中,,且与不平行,P、M、N分别是的中点,设面积为S,则S的范围是 .
17.在四边形中,AB∥CD,AD∥BC,、相交于点O,若,则线段的长度等于 .
18.在平行四边形ABCD中,比大,那么的度数为
19.如图,将平行四边形ABCD沿对角线AC翻折,点B落在点E处,CE与AD相交于点F,若AB=2,△CDF为等边三角形,则AC的长为 .
20.如图,中,为边上的中线,点在上,连接交于点,,,若,,则的长为 .
三、解答题
21.如图,平行四边形中,的平分线交于E,的平分线交于点F.
(1)求证:;
(2)若,,,求的长.
22.如图①所示, ABCD是某公园的平面示意图,A、B、C、D分别是该公园的四个入口,两条主干道AC、BD交于点O,经测量AB=0.5km,AC=1.2km,BD=1km,请你帮助公园的管理人员解决以下问题:
(1)公园的面积为 km2;
(2)如图②,公园管理人员在参观了武汉东湖绿道后,为提升游客游览的体验感,准备修建三条绿道AN、MN、CM,其中点M在OB上,点N在OD上,且BM=ON(点M与点O、B不重合),并计划在△AON与△COM两块绿地所在区域种植郁金香,求种植郁金香区域的面积;
(3)若修建(2)中的绿道每千米费用为10万元,请你计算该公园修建这三条绿道投入资金的最小值.
23.如图①所示,是某公园的平面示意图,分别是该公园的四个入口,两条主干道交于点,经测量,,,请你帮助公园的管理人员解决以下问题:
(1)公园的面积为 ;
(2)如图②,公园管理人员在参观了武汉东湖绿道后,为提升游客游览的体验感,准备修建三条绿道,其中点在上,点在上,且(点与点不重合),并计划在与两块绿地所在区域种植郁金香,求种植郁金香区域的面积;
(3)若修建(2)中的绿道每千米费用为10万元,请你画出该公园修建这三条绿道投入资金最小值时的图形.
24.如图,A、B两地被建筑物阻隔,为测量A、B两地的距离,连接、,分别取、的中点、.若的长为,求A、B两地的距离.
25.在一次数学探究活动中,小明用两条直线把平行四边形分割成四个部分,使含有一组对顶角的两个图形全等.
(1)请在图中的三个平行四边形中画出满足小明分割方法的直线;
(2)根据小明的分割方法,你认为把平行四边形分割成满足以上全等关系的直线有______组;由上述实验操作过程,你发现小明所画的两条直线的主要特点是______.
(3)拓展延伸:将一张平行四边形的纸片沿过对角线的中点的直线折叠,折痕交边、于点、,点落在点处,点落在点处.设交于点,分别交、于点、.求证:.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.D
2.C
3.B
4.B
5.A
6.A
7.C
8.D
9.C
10.D
11. 130° 50°
12./42度
13.②
14.1
15.-7,-3,3
16.
17.
18.
19.
20.
21.(1)略.
(2)13
22.(1)0.48;(2)0.12km2;(3)(+5)万元.
23.(1)(2)(3)略
24.
25.(1)略,(答案不唯一);
(2)无数,两条直线都经过平行四边形对角线的交点;
(3)略
答案第1页,共2页
答案第1页,共2页
