山东省烟台市莱州市第一中学2023-2024学年高一下学期6月月考试题 数学(含答案)
文档属性
| 名称 | 山东省烟台市莱州市第一中学2023-2024学年高一下学期6月月考试题 数学(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-19 13:23:11 | ||
图片预览



文档简介
2023级高一第四次质量检测数学试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知空间三条直线,若与垂直,与垂直,则( )
A.与异面 B.与相交
C.与平行 D.与平行、相交、异面均有可能
2.已知平面及空间中的任意一条直线,那么在平面内一定存在直线使得( )
A. B.与相交 C.与是异面直线 D.
3.如果数据的平均数是,方差是,则的平均数和方差分别是( )
A.与 B.和
C.和 D.和
4.如图,在三棱台中,从中取3个点确定平面,若平面平面,且,则所取的这3个点可以是( )
A. B. C. D.
5.是两个不同的平面,是两条不同的直线,下列命题中错误的是( )
A.若,则 B.若,则
C.若,则 D.若,则
6.某中学组织三个年级的学生进行党史知识竞赛.经统计,得到前200名学生分布的扇形图(如图)和前200名中高一学生排名分布的频率条形图(如图),则下列命题错误的是( )
A.成绩前200名的学生中,高一人数比高二人数多30人
B.成绩前100名的学生中,高一人数不超过50人
C.成绩前50名的学生中,高三人数不超过32人
D.成绩第51名到第100名的学生中,高二人数比高一人数多
7.已知在长方体中,,直线与平面所成角的正弦值为为线段的中点,则直线与直线所成角的余弦值为( )
A. B. C. D.
8.四棱锥中,,其余各棱的长均为2,则点到平面的距离为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.人均可支配收入和人均消费支出是两个非常重要的经济和民生指标,.常被用于衡量一个地区经济发展水平和群众生活水平.下图为2018~2023年前三季度全国城镇居民人均可支配收入及人均消费支出统计图,据此进行分析,则( )
A.2018~2023年前三季度全国城镇居民人均可支配收入逐年递增
B.2018~2023年前三季度全国城镇居民人均消费支出逐年递增
C.2018~2023年前三季度全国城镇居民人均可支配收入的极差比人均消费支出的极差大
D.2018~2023年前三季度全国城镇居民人均消费支出的中位数为20379元
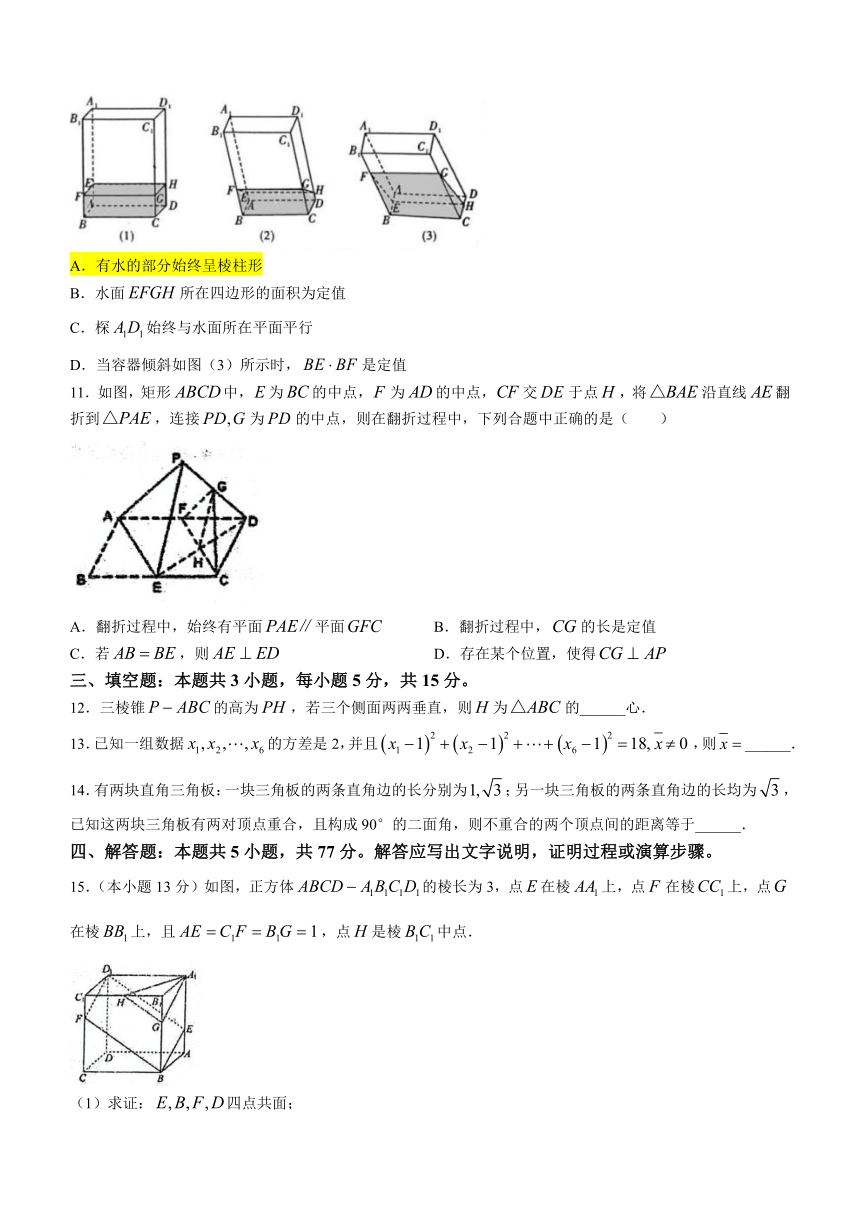
10.如下图,透明塑料制成的长方体容器内灌进一些水,固定容器底面一边于地面上,再将容器倾斜.随着倾斜度的不同,下列说法中正确的是( )
A.有水的部分始终呈棱柱形
B.水面所在四边形的面积为定值
C.棎始终与水面所在平面平行
D.当容器倾斜如图(3)所示时,是定值
11.如图,矩形中,为的中点,为的中点,交于点,将沿直线翻折到,连接为的中点,则在翻折过程中,下列合题中正确的是( )
A.翻折过程中,始终有平面平面 B.翻折过程中,的长是定值
C.若,则 D.存在某个位置,使得
三、填空题:本题共3小题,每小题5分,共15分。
12.三棱锥的高为,若三个侧面两两垂直,则为的______心.
13.已知一组数据的方差是2,并且,则______.
14.有两块直角三角板:一块三角板的两条直角边的长分别为;另一块三角板的两条直角边的长均为,已知这两块三角板有两对顶点重合,且构成90°的二面角,则不重合的两个顶点间的距离等于______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)如图,正方体的棱长为3,点在棱上,点在棱上,点在棱上,且,点是棱中点.
(1)求证:四点共面;
(2)求证:平面平面.
16.(本小题15分)如图所示,在直三棱柱中,分别为棱的中点.
(1)证明:平面;
(2)求与平面所成角的正弦值.
17.(本小题15分)某校高二年级的1000名学生参加了一次考试,考试成绩全部介于45分到95分之间,为统计学生的考试情况,从中随机抽取100名学生的考试成绩作为样本,得到的频率分布直方图如图所示.
(1)求m的值;
(2)估算这次考试成绩的平均分;
(3)从这1000名学生中选10名学生,已知他们上次考试成绩的平均分,标准差;记他们本次考试成绩的平均分,标准差,他们的本次考试成绩如表所示.判断他们的平均分是否显著提高(如果,则认为本次考试平均分较上次考试有显著提高,否则不认为显著提高).
这10名同学的本次考试成绩
70 72 72 72 74
71 72 72 72 73
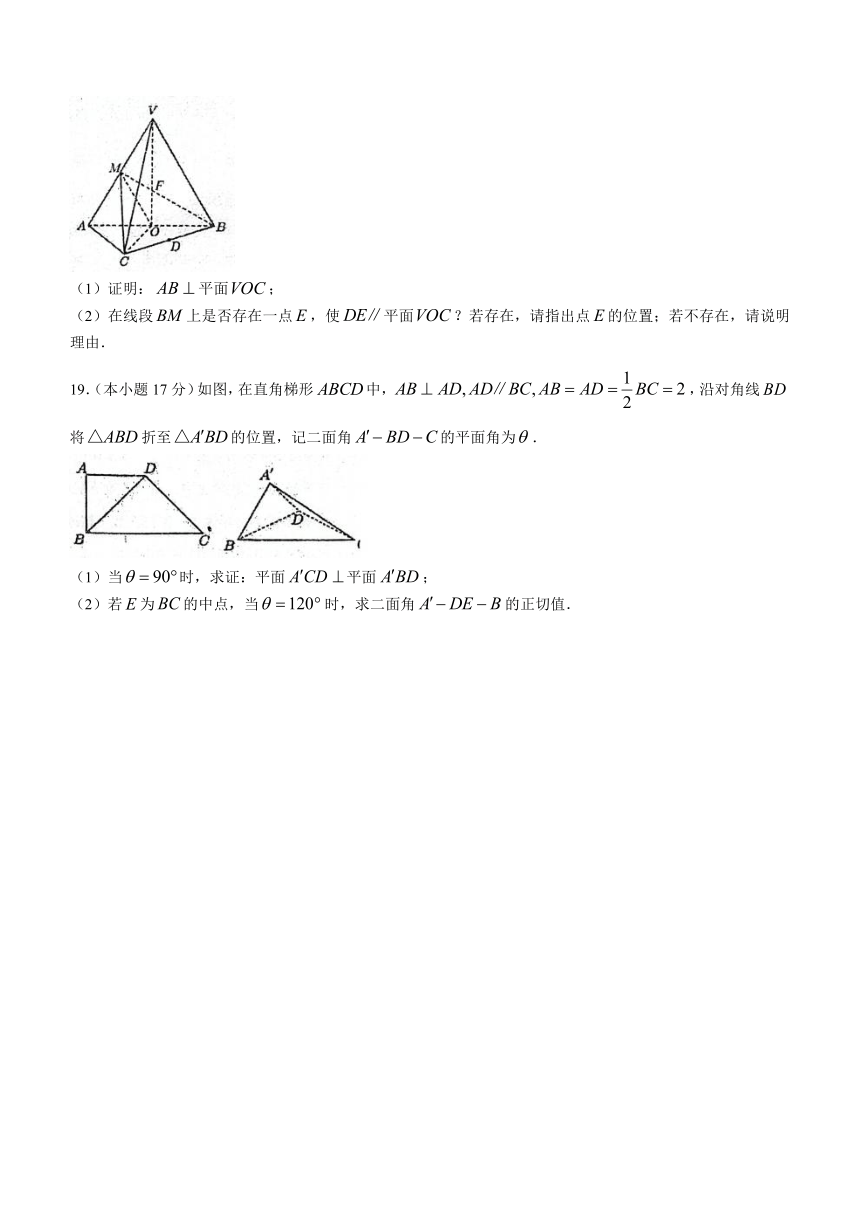
18.(本小题17分)如图,在三棱锥中,为等边三角形,且,分别为的中点,交于点.
(1)证明:平面;
(2)在线段上是否存在一点,使平面?若存在,请指出点的位置;若不存在,请说明理由.
19.(本小题17分)如图,在直角梯形中,,沿对角线将折至的位置,记二面角的平面角为.
(1)当时,求证:平面平面;
(2)若为的中点,当时,求二面角的正切值.
2023级高一第四次质量检测数学试题答案
一、DDCC CDAB
二、AC AC DABC
三、12.垂 13.2 14.2或
15.证明:(1)如图:在上取一点使得,
连接,则,
又因为,
所以四边形是平行四边形,
所以,
同理四边形是平行四边形,所以,且,
又,且,所以,
所以四边形是平行四边形,
所以,
所以,
所以四点共面;
(2)因为是的中点,所以,
因为,所以,
因为,且,
所以,
所以,
所以,
因为,
所以四边形为平行四边形,
所以,
因为平面平面,
平面平面,
所以平面平面
16.证明:(1)连接,取中点为点,连接,
分别为的中点,,
又为的中点,,
,则四边形为平行四边形,
,又平面平面,则平面;
(2)连接为中点,则,
又直三棱柱面,
面,则,
又面,
所以面,
由(1)知,面与平面所成角为,
易知:.∴,
则与平面所成角的正弦值为.
17.解:(1)由题可得,
解得.
(2)这次考试成绩的平均分约为.
(3),
,
则,
,
可以认为他们的平均分显著提高.
18.(1)证明:在三棱锥中,为等边三角形,且分别为的中点,
是的中点,
,
又是等边三角形,是的中点,
,
又平面,
平面;
解:(2)假设线段上存在一点使平面,连接,
平面,平面平面,
,
是的中点,
是的中点,
又是等边三角形的重心,
,
点是线段上靠近的三等分点.
19.解:(1)当时,平面平面.
在直角梯形中,,所以,所以,
因为平面平面平面,所以平面,
因为平面,所以平面平面,即证.
(2)取的中点,连接,因为,所以.
因为为的中点,连接,则为的中位线,所以.
因为,所以,
所以为二面角的平面角,即.
因为平面
所以平面.
因为平面,
所以平面平面.
因为平面平面,
所以过作,交于点,
则平面.
平面,过作与点,连结.
所以.
所以为二面角的平面角.
在中,.
在中,.
在中,,
所以,
故二面角的正切值为.
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知空间三条直线,若与垂直,与垂直,则( )
A.与异面 B.与相交
C.与平行 D.与平行、相交、异面均有可能
2.已知平面及空间中的任意一条直线,那么在平面内一定存在直线使得( )
A. B.与相交 C.与是异面直线 D.
3.如果数据的平均数是,方差是,则的平均数和方差分别是( )
A.与 B.和
C.和 D.和
4.如图,在三棱台中,从中取3个点确定平面,若平面平面,且,则所取的这3个点可以是( )
A. B. C. D.
5.是两个不同的平面,是两条不同的直线,下列命题中错误的是( )
A.若,则 B.若,则
C.若,则 D.若,则
6.某中学组织三个年级的学生进行党史知识竞赛.经统计,得到前200名学生分布的扇形图(如图)和前200名中高一学生排名分布的频率条形图(如图),则下列命题错误的是( )
A.成绩前200名的学生中,高一人数比高二人数多30人
B.成绩前100名的学生中,高一人数不超过50人
C.成绩前50名的学生中,高三人数不超过32人
D.成绩第51名到第100名的学生中,高二人数比高一人数多
7.已知在长方体中,,直线与平面所成角的正弦值为为线段的中点,则直线与直线所成角的余弦值为( )
A. B. C. D.
8.四棱锥中,,其余各棱的长均为2,则点到平面的距离为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.人均可支配收入和人均消费支出是两个非常重要的经济和民生指标,.常被用于衡量一个地区经济发展水平和群众生活水平.下图为2018~2023年前三季度全国城镇居民人均可支配收入及人均消费支出统计图,据此进行分析,则( )
A.2018~2023年前三季度全国城镇居民人均可支配收入逐年递增
B.2018~2023年前三季度全国城镇居民人均消费支出逐年递增
C.2018~2023年前三季度全国城镇居民人均可支配收入的极差比人均消费支出的极差大
D.2018~2023年前三季度全国城镇居民人均消费支出的中位数为20379元
10.如下图,透明塑料制成的长方体容器内灌进一些水,固定容器底面一边于地面上,再将容器倾斜.随着倾斜度的不同,下列说法中正确的是( )
A.有水的部分始终呈棱柱形
B.水面所在四边形的面积为定值
C.棎始终与水面所在平面平行
D.当容器倾斜如图(3)所示时,是定值
11.如图,矩形中,为的中点,为的中点,交于点,将沿直线翻折到,连接为的中点,则在翻折过程中,下列合题中正确的是( )
A.翻折过程中,始终有平面平面 B.翻折过程中,的长是定值
C.若,则 D.存在某个位置,使得
三、填空题:本题共3小题,每小题5分,共15分。
12.三棱锥的高为,若三个侧面两两垂直,则为的______心.
13.已知一组数据的方差是2,并且,则______.
14.有两块直角三角板:一块三角板的两条直角边的长分别为;另一块三角板的两条直角边的长均为,已知这两块三角板有两对顶点重合,且构成90°的二面角,则不重合的两个顶点间的距离等于______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)如图,正方体的棱长为3,点在棱上,点在棱上,点在棱上,且,点是棱中点.
(1)求证:四点共面;
(2)求证:平面平面.
16.(本小题15分)如图所示,在直三棱柱中,分别为棱的中点.
(1)证明:平面;
(2)求与平面所成角的正弦值.
17.(本小题15分)某校高二年级的1000名学生参加了一次考试,考试成绩全部介于45分到95分之间,为统计学生的考试情况,从中随机抽取100名学生的考试成绩作为样本,得到的频率分布直方图如图所示.
(1)求m的值;
(2)估算这次考试成绩的平均分;
(3)从这1000名学生中选10名学生,已知他们上次考试成绩的平均分,标准差;记他们本次考试成绩的平均分,标准差,他们的本次考试成绩如表所示.判断他们的平均分是否显著提高(如果,则认为本次考试平均分较上次考试有显著提高,否则不认为显著提高).
这10名同学的本次考试成绩
70 72 72 72 74
71 72 72 72 73
18.(本小题17分)如图,在三棱锥中,为等边三角形,且,分别为的中点,交于点.
(1)证明:平面;
(2)在线段上是否存在一点,使平面?若存在,请指出点的位置;若不存在,请说明理由.
19.(本小题17分)如图,在直角梯形中,,沿对角线将折至的位置,记二面角的平面角为.
(1)当时,求证:平面平面;
(2)若为的中点,当时,求二面角的正切值.
2023级高一第四次质量检测数学试题答案
一、DDCC CDAB
二、AC AC DABC
三、12.垂 13.2 14.2或
15.证明:(1)如图:在上取一点使得,
连接,则,
又因为,
所以四边形是平行四边形,
所以,
同理四边形是平行四边形,所以,且,
又,且,所以,
所以四边形是平行四边形,
所以,
所以,
所以四点共面;
(2)因为是的中点,所以,
因为,所以,
因为,且,
所以,
所以,
所以,
因为,
所以四边形为平行四边形,
所以,
因为平面平面,
平面平面,
所以平面平面
16.证明:(1)连接,取中点为点,连接,
分别为的中点,,
又为的中点,,
,则四边形为平行四边形,
,又平面平面,则平面;
(2)连接为中点,则,
又直三棱柱面,
面,则,
又面,
所以面,
由(1)知,面与平面所成角为,
易知:.∴,
则与平面所成角的正弦值为.
17.解:(1)由题可得,
解得.
(2)这次考试成绩的平均分约为.
(3),
,
则,
,
可以认为他们的平均分显著提高.
18.(1)证明:在三棱锥中,为等边三角形,且分别为的中点,
是的中点,
,
又是等边三角形,是的中点,
,
又平面,
平面;
解:(2)假设线段上存在一点使平面,连接,
平面,平面平面,
,
是的中点,
是的中点,
又是等边三角形的重心,
,
点是线段上靠近的三等分点.
19.解:(1)当时,平面平面.
在直角梯形中,,所以,所以,
因为平面平面平面,所以平面,
因为平面,所以平面平面,即证.
(2)取的中点,连接,因为,所以.
因为为的中点,连接,则为的中位线,所以.
因为,所以,
所以为二面角的平面角,即.
因为平面
所以平面.
因为平面,
所以平面平面.
因为平面平面,
所以过作,交于点,
则平面.
平面,过作与点,连结.
所以.
所以为二面角的平面角.
在中,.
在中,.
在中,,
所以,
故二面角的正切值为.
同课章节目录
