2025人教版高中物理必修第一册同步练习题(有解析)--第二章 匀变速直线运动的研究拔高练
文档属性
| 名称 | 2025人教版高中物理必修第一册同步练习题(有解析)--第二章 匀变速直线运动的研究拔高练 |

|
|
| 格式 | docx | ||
| 文件大小 | 579.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-06-20 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025人教版高中物理必修第一册
综合拔高练
五年高考练
考点1 匀变速直线运动规律的应用
1.(2023山东,6)如图所示,电动公交车做匀减速直线运动进站,连续经过R、S、T三点。已知ST段的距离是RS的两倍,RS段的平均速度是10 m/s,ST段的平均速度是5 m/s。则公交车经过T点时的瞬时速度为 ( )
A.3 m/s B.2 m/s C.1 m/s D.0.5 m/s
2.(2022全国甲,15)长为l的高速列车在平直轨道上正常行驶,速率为v0,要通过前方一长为L的隧道,当列车的任一部分处于隧道内时,列车速率都不允许超过v(vA. C.
3.(2022湖北,6)我国高铁技术全球领先,乘高铁极大节省了出行时间。假设两火车站W和G间的铁路里程为1 080 km,W和G之间还均匀分布了4个车站。列车从W站始发,经停4站后到达终点站G。设普通列车的最高速度为108 km/h,高铁列车的最高速度为324 km/h。若普通列车和高铁列车在进站和出站过程中,加速度大小均为0.5 m/s2,其余行驶时间内保持各自的最高速度匀速运动,两种列车在每个车站停车时间相同,则从W到G乘高铁列车出行比乘普通列车节省的时间为( )
A.6小时25分钟 B.6小时30分钟
C.6小时35分钟 D.6小时40分钟
考点2 x-t、v-t、a-t图像的综合应用
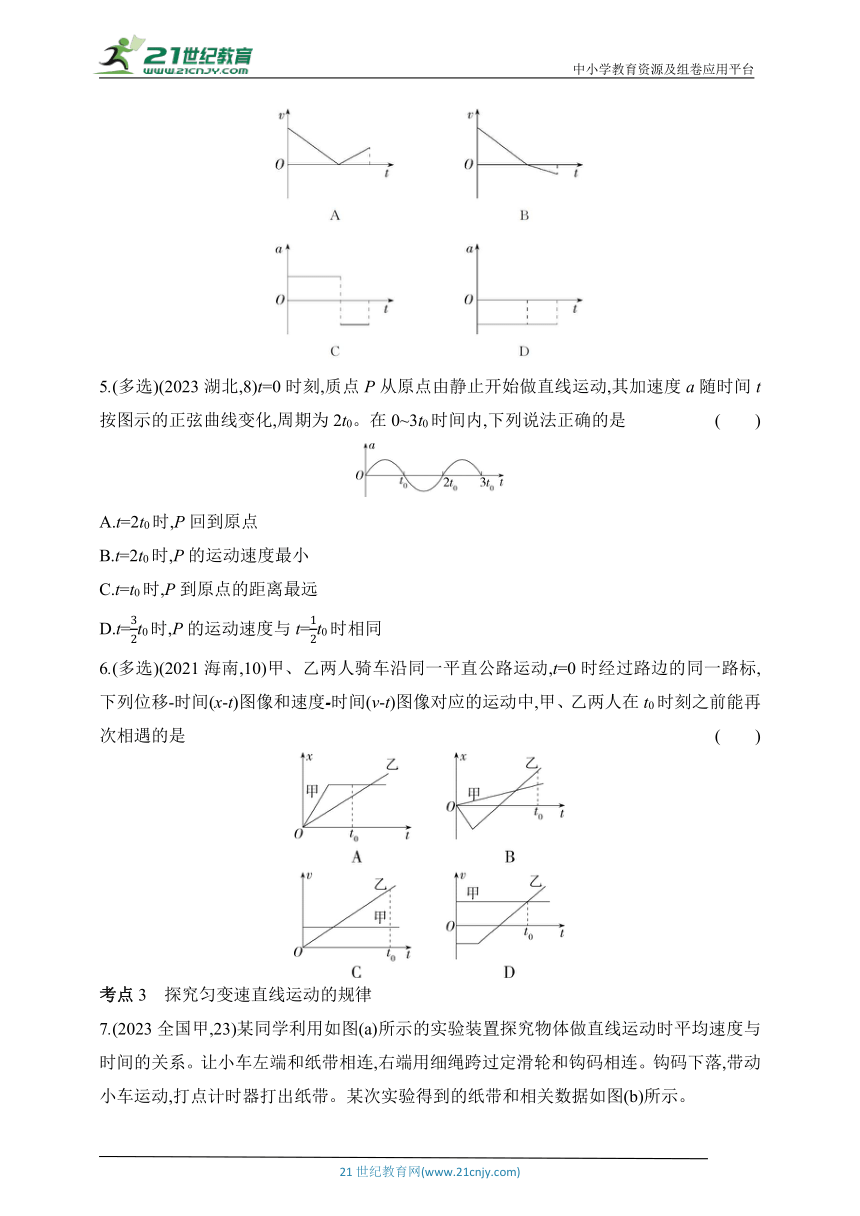
4.(2023广东,3)铯原子喷泉钟是定标“秒”的装置。在喷泉钟的真空系统中,可视为质点的铯原子团在激光的推动下,获得一定的初速度。随后激光关闭,铯原子团仅在重力的作用下做竖直上抛运动,到达最高点后再做一段自由落体运动。取竖直向上为正方向。下列可能表示激光关闭后铯原子团的速度v或加速度a随时间t变化的图像是 ( )
5.(多选)(2023湖北,8)t=0时刻,质点P从原点由静止开始做直线运动,其加速度a随时间t按图示的正弦曲线变化,周期为2t0。在0~3t0时间内,下列说法正确的是 ( )
A.t=2t0时,P回到原点
B.t=2t0时,P的运动速度最小
C.t=t0时,P到原点的距离最远
D.t=t0时,P的运动速度与t=t0时相同
6.(多选)(2021海南,10)甲、乙两人骑车沿同一平直公路运动,t=0时经过路边的同一路标,下列位移-时间(x-t)图像和速度 时间(v-t)图像对应的运动中,甲、乙两人在t0时刻之前能再次相遇的是 ( )
考点3 探究匀变速直线运动的规律
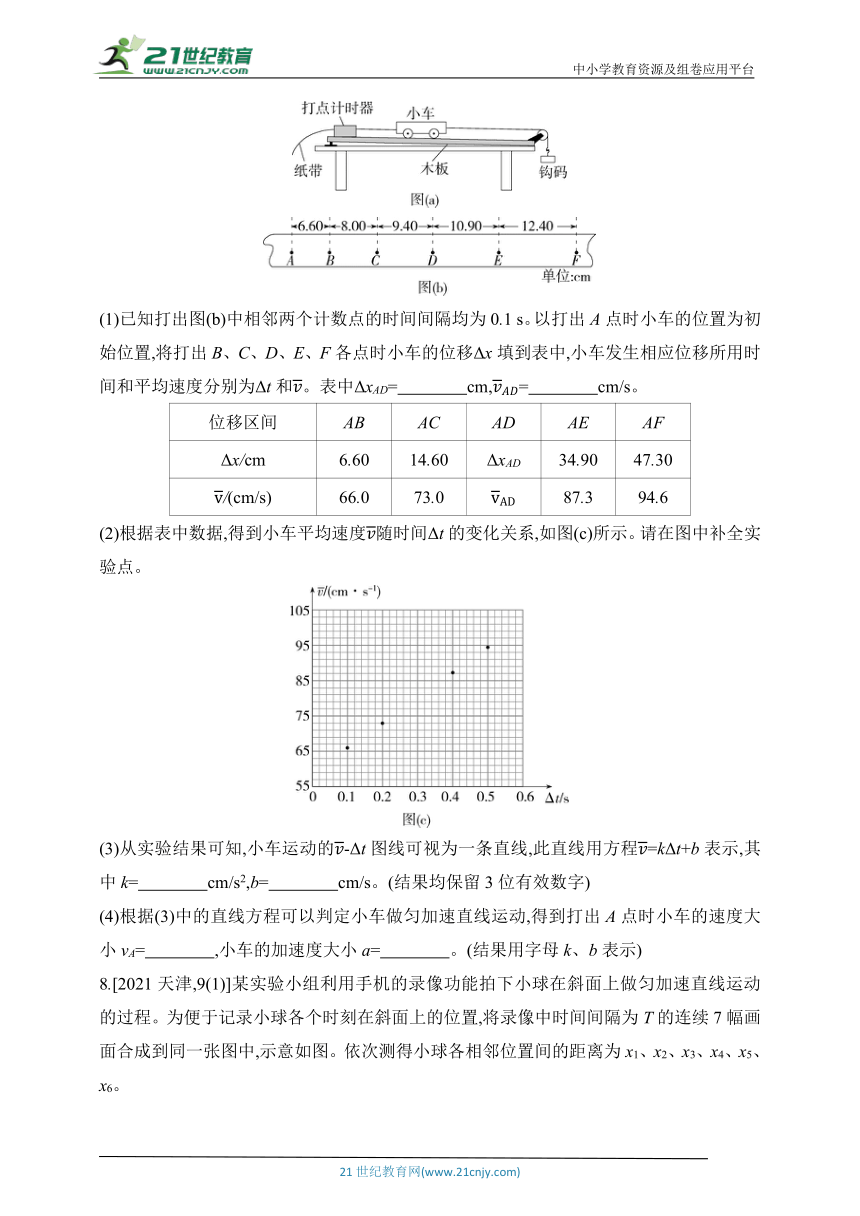
7.(2023全国甲,23)某同学利用如图(a)所示的实验装置探究物体做直线运动时平均速度与时间的关系。让小车左端和纸带相连,右端用细绳跨过定滑轮和钩码相连。钩码下落,带动小车运动,打点计时器打出纸带。某次实验得到的纸带和相关数据如图(b)所示。
(1)已知打出图(b)中相邻两个计数点的时间间隔均为0.1 s。以打出A点时小车的位置为初始位置,将打出B、C、D、E、F各点时小车的位移Δx填到表中,小车发生相应位移所用时间和平均速度分别为Δt和。表中ΔxAD= cm,= cm/s。
位移区间 AB AC AD AE AF
Δx/cm 6.60 14.60 ΔxAD 34.90 47.30
/(cm/s) 66.0 73.0 87.3 94.6
(2)根据表中数据,得到小车平均速度随时间Δt的变化关系,如图(c)所示。请在图中补全实验点。
(3)从实验结果可知,小车运动的-Δt图线可视为一条直线,此直线用方程=kΔt+b表示,其中k= cm/s2,b= cm/s。(结果均保留3位有效数字)
(4)根据(3)中的直线方程可以判定小车做匀加速直线运动,得到打出A点时小车的速度大小vA= ,小车的加速度大小a= 。(结果用字母k、b表示)
8.[2021天津,9(1)]某实验小组利用手机的录像功能拍下小球在斜面上做匀加速直线运动的过程。为便于记录小球各个时刻在斜面上的位置,将录像中时间间隔为T的连续7幅画面合成到同一张图中,示意如图。依次测得小球各相邻位置间的距离为x1、x2、x3、x4、x5、x6。
①写出小球在位置1的速度表达式 。
②要求充分利用测量数据,写出小球运动过程中的加速度表达式 。
③在测量小球相邻位置间距时由于实验者读数产生的误差是 误差。(填“偶然”或“系统”)
三年模拟练
应用实践
1.(2024河南普高联考月考)在某次百米赛跑中,甲、乙两个同学从同一起跑线同时起跑,前50 m的速度 时间图像如图所示,此后两个同学均做匀速直线运动至终点线,已知图中阴影Ⅰ的面积大于阴影Ⅱ的面积,由此可知( )
A.甲同学先做匀加速运动后做匀速运动
B.在t1时刻甲、乙两同学相遇
C.在t2时刻甲同学在乙同学前面
D.甲同学一定先到达终点线
2.(2024河南省实验中学期中)历史上有些科学家曾把在任意相等位移内速度变化量相等的单向直线运动称为“匀变速直线运动”(现称“另类匀变速直线运动”),“另类加速度”定义为A=,其中v0和vt分别表示某段位移s内的初速度和末速度。A>0表示物体做加速运动,A<0表示物体做减速运动。而现在物理学中加速度定义式为a=,下列说法正确的是 ( )
A.若A不变,则a也不变
B.若A>0且保持不变,则a逐渐变小
C.若A不变,则物体在中间位置处速度大小为
D.若A不变,则物体在中间位置处速度大小为
3.(多选)(2024广东东莞中学月考)有一种叫作“滚钱”的游戏,具体操作是在水平桌面放置不同金额的纸币,瓶子滚到哪张纸币就可以赢取此金额,如图甲所示。现用图乙来描述这个模型,滚瓶从水平桌面上O点出发,途中经过A、B、C、D、E 5个放钱的位置,相邻两个位置间的距离均为0.2 m。设滚瓶(可视为质点)在桌面上做匀变速运动,小马同学以v0=1 m/s的速度推出滚瓶,最后刚好停在E处。已知滚瓶在D点和E点之间滑行的时间为1 s,则下列说法正确的是( )
A.滚瓶从A到E的时间是从D到E的时间的2倍
B.滚瓶在各点的速度比满足vA∶vB∶vC∶vD=4∶3∶2∶1
C.滚瓶在桌面上运动的加速度大小为0.4 m/s2
D.若以0.9 m/s的速度将滚瓶推出,滚瓶最终将停在B、C之间
4.(多选)(2024四川成都第七中学月考)甲图为在同一直线上运动的M、N两质点的位置(x)随时间(t)变化的图像,乙图为质点N的速度(v)随时间(t)变化的图像,甲图中直线M与曲线N相切于c点,以下说法正确的是( )
A.质点N的加速度大小为2.5 m/s2
B.t=4 s时质点N的速度为零
C.t=0时,质点M、N之间的距离为75 m
D.当质点N的速度为零时,质点M、N之间的距离为51 m
5.(2024四川成都简阳实验中学等期中联考)在国庆节前,小华驾驶一辆汽车从成都通过高速收费站外出旅游。其过程可简化为如图:汽车以v0=15 m/s的速度匀速行驶,车头至位置A(图中未标出)时开始刹车到停止,此时发现前面还有3辆车排队等候,第一辆车车头刚好位于收费窗口停车线,司机开始领取通行卡。假设所有车辆的长度均为L=4.5 m,前后两车均相距L0=1.5 m。在收费窗口停车线前,所有车辆由静止同时开始加速,然后减速停止,依次至车头到达收费窗口停车线,前后两车间距保持不变,领取通行卡后立即加速离开,领卡时间均为t0=10 s,最后小华领取通行卡后将汽车加速到v0,此时车头到达位置B(图中未标出)。所有车辆加速和减速过程均视为匀变速直线运动,加速度大小均为a=1.5 m/s2。
(1)求第二辆车从启动至车头到达收费窗口停车线经过的时间。
(2)求位置A、B间的距离;
(3)在国庆节期间,小华驾驶的汽车可以免费通行。车头到达位置A时,汽车以v0=15 m/s的速度匀速行驶,至车头到达位置C(图中未标出)时开始减速,速度降到v=6 m/s,再匀速行驶d=12 m,至车头到达收费窗口停车线,然后加速到v0,再匀速行驶至车头到达位置B。设加速过程和减速过程的加速度大小仍为a=1.5 m/s2,求小华现在从位置A到位置B比之前排队节约的时间。
迁移创新
6.(2024北京交通大学附属中学期中)“科技让生活更美丽”,自动驾驶汽车呈现出接近实用化的趋势。图1为某型号无人驾驶的智能汽车的测试照,为了增加乘员乘坐舒适性,程序设定汽车制动时汽车加速度大小随位移均匀变化。某次测试汽车“a-x”关系图线如图2所示,汽车制动距离为12 m。
(1)判断汽车做什么运动;
(2)微元法是一种常用的研究方法,对于直线运动,教科书中讲解了如何由v-t图像来求位移。请你借鉴此方法,求汽车的初速度v0的大小。
(3)为了求汽车的制动时间t,某同学的求解过程如下:
在制动过程中加速度的平均值为 m/s2=3 m/s2
将减速过程看成反向加速过程,根据运动学公式x=t2,得t=2 s
请你判断该同学的做法是否正确,并说明理由。
答案与分层梯度式解析
五年高考练
1.C 2.C 3.B 4.D 5.BD 6.BC
1.C 在匀变速直线运动中,某段时间内的平均速度等于该段时间初末速度之和的一半,则有,由此知vS=10 m/s-vT,vR=10 m/s+vT,又有=2axRS,=2axST,2xRS=xST,知vT=1 m/s,故C正确。
一题多解 利用匀变速直线运动一段时间内的平均速度等于该段时间中间时刻的瞬时速度快速求解。电动公交车做匀减速直线运动,设加速度大小为a,RS间的距离为x,则ST段的距离为2x,根据题意有=10 m/s,=5 m/s,联立解得t2=4t1;RS中间时刻的速度=10 m/s,ST中间时刻的速度=5 m/s;从RS中间时刻减速到ST中间时刻过程,有5 m/s=10 m/s-a(+2t1),解得at1=2 m/s,从ST中间时刻减速到T位置过程,有vT=5 m/s-a·2t1=1 m/s,故选C。
2.C 图形剖析
根据题意画出所用时间最短时列车运动的示意图以及相应的v-t图像。
列车从减速开始至回到正常行驶速率v。所用时间最短时,列车车头到达隧道前减速时间Δt1=,在隧道中匀速行驶时间Δt2=,车尾离开隧道后,加速时间Δt3=,总时间t总=Δt1+Δt2+Δt3=,故C项正确。
3.B 设列车最高速度为v,匀加速及匀减速运动时间均为t1,匀速运动时间为t2,两相邻车站间距为L,则列车从W到G的运行时间为t=5(t2+2t1)=5×,由题意可知L= km=2.16×105 m,两列车在每站停车时间相同,故节省的时间Δt= s- s=6 h 30 min,故B正确。
方法技巧 画出列车在相邻两站间运动的v-t图像如图所示,将右侧阴影部分移到左侧,则原梯形可以转化为矩形,其面积表示相邻两站间的距离L,则vt=L,则列车在相邻两站间运动的时间为t+t1,相邻两站间节省的时间Δt=,将v=30 m/s,v'=90 m/s,t1==60 s,t1'==180 s代入,解得相邻两站间节省的时间Δt=4 680 s,因此总的节省时间Δt总=5Δt=5×4 680 s=6 h 30 min,故选B。
4.D 铯原子团仅受重力,加速度为g且竖直向下,故C错误,D正确。在v t图像中,图线的斜率表示加速度,故斜率不变,图线应是一条倾斜的直线,A、B均错误。
5.BD 0~2t0时间内,质点P一直沿着正方向运动,则t=2t0时P未回到原点,A错误;将a-t图像转化为如图所示的v-t图像,可以看出t=2t0时,P的运动速度最小,B正确;t=3t0时,P 到原点的距离最远,C错误;t=t0时P的运动速度与t=t0时的相同,D正确。
6.BC 甲、乙t=0时刻经过同一位置,t0前能再次相遇,说明t0前存在位移相等的时刻,反映到x-t图像中就是图线有交点,反映到v-t图像中就是图线与时间轴围成的面积相等。A项图中,在t0时刻之前甲、乙位移没有相等的时刻,即两人在t0时刻之前不能相遇,A不符合题意;B项图中,在t0时刻之前图线有交点(同一时间到达同一位置),即在交点对应的时刻甲、乙两人位移相等,即两人在t0时刻之前能再次相遇,B符合题意;v-t图像与横轴围成的面积表示位移,C项图中,甲、乙在t0时刻之前位移有相等的时刻,即两人能再次相遇,C符合题意;由D项图像可知在t0时刻之前,甲的位移始终大于乙的位移,则两人不能相遇,D不符合题意。
7.答案 (1)24.00 80.0 (2)见解析
(3)70.6(70.0~71.2均正确) 59.0 (4)b 2k
解析 (1)由纸带上的数据可得ΔxAD=6.60 cm+8.00 cm+9.40 cm=24.00 cm,平均速度=80.0 cm/s。
(2)描点连线,作出的图像如图所示。
(3)=kΔt+b中k表示图线斜率,b表示图线纵截距,由-Δt图线可得k≈70.6 cm/s2,b=59.0 cm/s。
(4)由=kΔt+b得Δx=k(Δt)2+bΔt,对比x=at2+v0t,可得初速度vA=b,加速度a=2k。
高考风向 利用打点计时器测量速度、加速度是高考的常考内容,如2023年浙江1月选考第16题Ⅰ、2022年北京卷第16题等,都考查了此类问题。一般以物体做直线运动来设计学习探索问题情境,考查学生分析打点计时器所打纸带的计数点间距离和小车位移、所用时间和平均速度大小的关系,在此基础上总结实验规律并求出相关的物理量。要用到的物理知识有:某段时间内中间时刻的瞬时速度用这段时间内的平均速度来表示、用逐差法计算加速度、图像法的利用等。
8.答案 ① ③偶然
解析 ①匀变速直线运动中,中间时刻速度等于平均速度,所以小球在位置1的速度为v1=
②题中要求充分利用数据,利用逐差法求解加速度,则x4-x1=3a1T2,x5-x2=3a2T2,x6-x3=3a3T2,解得加速度为a=
③读数产生的误差是人为因素造成的,属于偶然误差。
三年模拟练
1.C 2.D 3.AC 4.BC
1.C 在v-t图像中,图线的斜率表示加速度,由图可知,甲同学先做加速度减小的加速运动后做匀速运动,A错误。在v-t图像中图线与横轴所围的面积表示位移,甲、乙两个同学从同一起跑线同时起跑,t1时间内,甲运动的位移大于乙运动的位移,故t1时刻甲同学在乙同学前面;阴影Ⅰ的面积表示t1时间内甲比乙多运动的距离,阴影Ⅱ的面积表示t1到t2时间内乙比甲多运动的距离,由于阴影Ⅰ的面积大于阴影Ⅱ的面积,因此在t2时间内甲同学运动的位移大于乙同学运动的位移,所以在t2时刻甲同学在乙同学前面,B错误,C正确;t2时刻后乙的速度大于甲的速度,所以后50 m乙同学有可能超过甲同学先到达终点,D错误。
2.D 若A不变,有两种情况,第一种情况是A>0,相等位移内速度增加量相等,平均速度越来越大,所以相等位移内用的时间越来越短,由a=可知,a越来越大;第二种情况是A<0,在这种情况下,相等位移内速度减少量相等,平均速度越来越小,所以相等位移内用的时间越来越长,由a=可知,a越来越小,A、B错误;若A不变,即相等位移内速度变化量相等,所以通过前半段位移过程中,速度变化量为,所以中间位置的速度为,C错误,D正确。
3.AC
关键点拨
滚瓶做末速度为零的匀减速直线运动,采用逆向思维,利用等位移的运动规律求解。
设滚瓶依次经过A、B、C、D、E两相邻位置的时间间隔分别为t1、t2、t3和t4,根据逆向思维可知t4∶t3∶t2∶t1=1∶(-1)∶()∶(2-),而t4=1 s,故滚瓶由位置A到E所用的时间t=t4+t3+t2+t1=2 s,即滚瓶从A到E的时间是从D到E的时间的2倍,A正确。根据v2=2ax可知滚瓶在各点的速度比满足vA∶vB∶vC∶vD=2∶∶1,B错误。滚瓶由位置D到E,由x=可得a=0.4 m/s2,C正确。滚瓶从O点到位置E,有xOE= m=1.25 m,所以xOA=0.45 m,xOB=0.65 m,xOC=0.85 m,xOD=1.05 m;若以0.9 m/s的速度将滚瓶推出,滚瓶运动的位移为x'= m=1.012 5 m,xOC4.BC 根据题意,设质点N的加速度大小为a,初速度为v0,由速度公式v=v0+at结合题图乙有v0+10a=9 m/s;由位移公式x=v0t+at2结合题图甲有(21-6) m=10v0+×a×102,联立得v0=-6 m/s,a=1.5 m/s2,故A错误。根据速度公式v=v0+at可得,t=4 s时质点N的速度为v4=(-6+4×1.5) m/s=0,故B正确。题图甲中直线M与曲线N相切于c点,可知质点M的速度与质点N在t=10 s时的速度相等,即vM=v10=9 m/s;设质点M的初位置坐标为x1,则有vM=,解得x1=-69 m,则t=0时,质点M、N之间的距离为6 m-(-69 m)=75 m,C正确。由B项分析可知,t=4 s时质点N的速度为0,0~4 s内质点N的位移为x4N=-12 m,质点M的位移为x4M=vMt=36 m(点拨:M、N相向运动),可知t=4 s时质点M、N之间的距离为Δx=(75-12-36) m=27 m,D错误。
5.答案 (1)4 s (2)168 m (3)56 s
解析 (1)每一辆车做一次匀加速运动和一次匀减速运动的时间均相等,设为Δt,则有aΔt2,可得Δt=2 s
设第二辆车从启动至车头到达收费窗口停车线经过的时间为t1,则有t1=2Δt=4 s
(2)设小华从开始刹车到刚好停止的时间为t2,运动的位移大小为x1,则有t2==10 s
x1=t2=75 m
此时车头到收费窗口停车线的距离为d1=3(L+L0)=18 m
离开后汽车加速到v0,运动的位移大小x2=x1=75 m
位置A、B间的距离x3=x1+d1+x2=168 m
(3)小华在国庆节前从位置A到位置B运动的v-t图像如图所示:
从位置A到位置B的时间t3=2t2+4t0+3×2Δt=72 s
小华在国庆节期间从位置A到位置B运动的v-t图像如图所示:
速度从v0减到v的时间t4==6 s,位移大小x4=t4=63 m
匀速运动至停车线所用时间t5==2 s
汽车速度恢复到v0的时间t6=t4=6 s
故节约的时间Δt'=t3-(t4+t5+t6+)
可得Δt'=56 s。
6.答案 (1)加速度逐渐增大的减速运动
(2)6 m/s (3)见解析
解析 (1)由图2可知汽车制动过程,其加速度a随位移x均匀增大,汽车做加速度逐渐增大的减速运动。
(2)由匀变速直线运动的速度与位移的关系可得v2-=-2ax
汽车做非匀变速直线运动,运用“微元法”,可知“a-x”图线与x轴所围图形的“面积”即“速度平方变化量的一半”(破题关键),即 m2·s-2
解得v0=6 m/s
(3)该同学的做法不正确;汽车以大小为3 m/s2的加速度做匀减速运动时,v-t图像如图中直线所示;位移不变,即v-t图线与t轴围成的面积不变;由a-x图像可知,加速度随位移均匀增大,对应的v-t图线如图中曲线所示,可得实际制动时间一定小于2 s。
知识迁移 本题涉及微元法,将课本中“v-t”图线与t轴所围图形的“面积”表示物体的位移的方法进行知识迁移,得出“a-x”图线与x轴所围图形的“面积”的物理意义,从而得出汽车的初速度大小。由此可见,运用合适的物理方法,巧妙利用图像处理物理问题在物理学习中特别重要。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教版高中物理必修第一册
综合拔高练
五年高考练
考点1 匀变速直线运动规律的应用
1.(2023山东,6)如图所示,电动公交车做匀减速直线运动进站,连续经过R、S、T三点。已知ST段的距离是RS的两倍,RS段的平均速度是10 m/s,ST段的平均速度是5 m/s。则公交车经过T点时的瞬时速度为 ( )
A.3 m/s B.2 m/s C.1 m/s D.0.5 m/s
2.(2022全国甲,15)长为l的高速列车在平直轨道上正常行驶,速率为v0,要通过前方一长为L的隧道,当列车的任一部分处于隧道内时,列车速率都不允许超过v(v
3.(2022湖北,6)我国高铁技术全球领先,乘高铁极大节省了出行时间。假设两火车站W和G间的铁路里程为1 080 km,W和G之间还均匀分布了4个车站。列车从W站始发,经停4站后到达终点站G。设普通列车的最高速度为108 km/h,高铁列车的最高速度为324 km/h。若普通列车和高铁列车在进站和出站过程中,加速度大小均为0.5 m/s2,其余行驶时间内保持各自的最高速度匀速运动,两种列车在每个车站停车时间相同,则从W到G乘高铁列车出行比乘普通列车节省的时间为( )
A.6小时25分钟 B.6小时30分钟
C.6小时35分钟 D.6小时40分钟
考点2 x-t、v-t、a-t图像的综合应用
4.(2023广东,3)铯原子喷泉钟是定标“秒”的装置。在喷泉钟的真空系统中,可视为质点的铯原子团在激光的推动下,获得一定的初速度。随后激光关闭,铯原子团仅在重力的作用下做竖直上抛运动,到达最高点后再做一段自由落体运动。取竖直向上为正方向。下列可能表示激光关闭后铯原子团的速度v或加速度a随时间t变化的图像是 ( )
5.(多选)(2023湖北,8)t=0时刻,质点P从原点由静止开始做直线运动,其加速度a随时间t按图示的正弦曲线变化,周期为2t0。在0~3t0时间内,下列说法正确的是 ( )
A.t=2t0时,P回到原点
B.t=2t0时,P的运动速度最小
C.t=t0时,P到原点的距离最远
D.t=t0时,P的运动速度与t=t0时相同
6.(多选)(2021海南,10)甲、乙两人骑车沿同一平直公路运动,t=0时经过路边的同一路标,下列位移-时间(x-t)图像和速度 时间(v-t)图像对应的运动中,甲、乙两人在t0时刻之前能再次相遇的是 ( )
考点3 探究匀变速直线运动的规律
7.(2023全国甲,23)某同学利用如图(a)所示的实验装置探究物体做直线运动时平均速度与时间的关系。让小车左端和纸带相连,右端用细绳跨过定滑轮和钩码相连。钩码下落,带动小车运动,打点计时器打出纸带。某次实验得到的纸带和相关数据如图(b)所示。
(1)已知打出图(b)中相邻两个计数点的时间间隔均为0.1 s。以打出A点时小车的位置为初始位置,将打出B、C、D、E、F各点时小车的位移Δx填到表中,小车发生相应位移所用时间和平均速度分别为Δt和。表中ΔxAD= cm,= cm/s。
位移区间 AB AC AD AE AF
Δx/cm 6.60 14.60 ΔxAD 34.90 47.30
/(cm/s) 66.0 73.0 87.3 94.6
(2)根据表中数据,得到小车平均速度随时间Δt的变化关系,如图(c)所示。请在图中补全实验点。
(3)从实验结果可知,小车运动的-Δt图线可视为一条直线,此直线用方程=kΔt+b表示,其中k= cm/s2,b= cm/s。(结果均保留3位有效数字)
(4)根据(3)中的直线方程可以判定小车做匀加速直线运动,得到打出A点时小车的速度大小vA= ,小车的加速度大小a= 。(结果用字母k、b表示)
8.[2021天津,9(1)]某实验小组利用手机的录像功能拍下小球在斜面上做匀加速直线运动的过程。为便于记录小球各个时刻在斜面上的位置,将录像中时间间隔为T的连续7幅画面合成到同一张图中,示意如图。依次测得小球各相邻位置间的距离为x1、x2、x3、x4、x5、x6。
①写出小球在位置1的速度表达式 。
②要求充分利用测量数据,写出小球运动过程中的加速度表达式 。
③在测量小球相邻位置间距时由于实验者读数产生的误差是 误差。(填“偶然”或“系统”)
三年模拟练
应用实践
1.(2024河南普高联考月考)在某次百米赛跑中,甲、乙两个同学从同一起跑线同时起跑,前50 m的速度 时间图像如图所示,此后两个同学均做匀速直线运动至终点线,已知图中阴影Ⅰ的面积大于阴影Ⅱ的面积,由此可知( )
A.甲同学先做匀加速运动后做匀速运动
B.在t1时刻甲、乙两同学相遇
C.在t2时刻甲同学在乙同学前面
D.甲同学一定先到达终点线
2.(2024河南省实验中学期中)历史上有些科学家曾把在任意相等位移内速度变化量相等的单向直线运动称为“匀变速直线运动”(现称“另类匀变速直线运动”),“另类加速度”定义为A=,其中v0和vt分别表示某段位移s内的初速度和末速度。A>0表示物体做加速运动,A<0表示物体做减速运动。而现在物理学中加速度定义式为a=,下列说法正确的是 ( )
A.若A不变,则a也不变
B.若A>0且保持不变,则a逐渐变小
C.若A不变,则物体在中间位置处速度大小为
D.若A不变,则物体在中间位置处速度大小为
3.(多选)(2024广东东莞中学月考)有一种叫作“滚钱”的游戏,具体操作是在水平桌面放置不同金额的纸币,瓶子滚到哪张纸币就可以赢取此金额,如图甲所示。现用图乙来描述这个模型,滚瓶从水平桌面上O点出发,途中经过A、B、C、D、E 5个放钱的位置,相邻两个位置间的距离均为0.2 m。设滚瓶(可视为质点)在桌面上做匀变速运动,小马同学以v0=1 m/s的速度推出滚瓶,最后刚好停在E处。已知滚瓶在D点和E点之间滑行的时间为1 s,则下列说法正确的是( )
A.滚瓶从A到E的时间是从D到E的时间的2倍
B.滚瓶在各点的速度比满足vA∶vB∶vC∶vD=4∶3∶2∶1
C.滚瓶在桌面上运动的加速度大小为0.4 m/s2
D.若以0.9 m/s的速度将滚瓶推出,滚瓶最终将停在B、C之间
4.(多选)(2024四川成都第七中学月考)甲图为在同一直线上运动的M、N两质点的位置(x)随时间(t)变化的图像,乙图为质点N的速度(v)随时间(t)变化的图像,甲图中直线M与曲线N相切于c点,以下说法正确的是( )
A.质点N的加速度大小为2.5 m/s2
B.t=4 s时质点N的速度为零
C.t=0时,质点M、N之间的距离为75 m
D.当质点N的速度为零时,质点M、N之间的距离为51 m
5.(2024四川成都简阳实验中学等期中联考)在国庆节前,小华驾驶一辆汽车从成都通过高速收费站外出旅游。其过程可简化为如图:汽车以v0=15 m/s的速度匀速行驶,车头至位置A(图中未标出)时开始刹车到停止,此时发现前面还有3辆车排队等候,第一辆车车头刚好位于收费窗口停车线,司机开始领取通行卡。假设所有车辆的长度均为L=4.5 m,前后两车均相距L0=1.5 m。在收费窗口停车线前,所有车辆由静止同时开始加速,然后减速停止,依次至车头到达收费窗口停车线,前后两车间距保持不变,领取通行卡后立即加速离开,领卡时间均为t0=10 s,最后小华领取通行卡后将汽车加速到v0,此时车头到达位置B(图中未标出)。所有车辆加速和减速过程均视为匀变速直线运动,加速度大小均为a=1.5 m/s2。
(1)求第二辆车从启动至车头到达收费窗口停车线经过的时间。
(2)求位置A、B间的距离;
(3)在国庆节期间,小华驾驶的汽车可以免费通行。车头到达位置A时,汽车以v0=15 m/s的速度匀速行驶,至车头到达位置C(图中未标出)时开始减速,速度降到v=6 m/s,再匀速行驶d=12 m,至车头到达收费窗口停车线,然后加速到v0,再匀速行驶至车头到达位置B。设加速过程和减速过程的加速度大小仍为a=1.5 m/s2,求小华现在从位置A到位置B比之前排队节约的时间。
迁移创新
6.(2024北京交通大学附属中学期中)“科技让生活更美丽”,自动驾驶汽车呈现出接近实用化的趋势。图1为某型号无人驾驶的智能汽车的测试照,为了增加乘员乘坐舒适性,程序设定汽车制动时汽车加速度大小随位移均匀变化。某次测试汽车“a-x”关系图线如图2所示,汽车制动距离为12 m。
(1)判断汽车做什么运动;
(2)微元法是一种常用的研究方法,对于直线运动,教科书中讲解了如何由v-t图像来求位移。请你借鉴此方法,求汽车的初速度v0的大小。
(3)为了求汽车的制动时间t,某同学的求解过程如下:
在制动过程中加速度的平均值为 m/s2=3 m/s2
将减速过程看成反向加速过程,根据运动学公式x=t2,得t=2 s
请你判断该同学的做法是否正确,并说明理由。
答案与分层梯度式解析
五年高考练
1.C 2.C 3.B 4.D 5.BD 6.BC
1.C 在匀变速直线运动中,某段时间内的平均速度等于该段时间初末速度之和的一半,则有,由此知vS=10 m/s-vT,vR=10 m/s+vT,又有=2axRS,=2axST,2xRS=xST,知vT=1 m/s,故C正确。
一题多解 利用匀变速直线运动一段时间内的平均速度等于该段时间中间时刻的瞬时速度快速求解。电动公交车做匀减速直线运动,设加速度大小为a,RS间的距离为x,则ST段的距离为2x,根据题意有=10 m/s,=5 m/s,联立解得t2=4t1;RS中间时刻的速度=10 m/s,ST中间时刻的速度=5 m/s;从RS中间时刻减速到ST中间时刻过程,有5 m/s=10 m/s-a(+2t1),解得at1=2 m/s,从ST中间时刻减速到T位置过程,有vT=5 m/s-a·2t1=1 m/s,故选C。
2.C 图形剖析
根据题意画出所用时间最短时列车运动的示意图以及相应的v-t图像。
列车从减速开始至回到正常行驶速率v。所用时间最短时,列车车头到达隧道前减速时间Δt1=,在隧道中匀速行驶时间Δt2=,车尾离开隧道后,加速时间Δt3=,总时间t总=Δt1+Δt2+Δt3=,故C项正确。
3.B 设列车最高速度为v,匀加速及匀减速运动时间均为t1,匀速运动时间为t2,两相邻车站间距为L,则列车从W到G的运行时间为t=5(t2+2t1)=5×,由题意可知L= km=2.16×105 m,两列车在每站停车时间相同,故节省的时间Δt= s- s=6 h 30 min,故B正确。
方法技巧 画出列车在相邻两站间运动的v-t图像如图所示,将右侧阴影部分移到左侧,则原梯形可以转化为矩形,其面积表示相邻两站间的距离L,则vt=L,则列车在相邻两站间运动的时间为t+t1,相邻两站间节省的时间Δt=,将v=30 m/s,v'=90 m/s,t1==60 s,t1'==180 s代入,解得相邻两站间节省的时间Δt=4 680 s,因此总的节省时间Δt总=5Δt=5×4 680 s=6 h 30 min,故选B。
4.D 铯原子团仅受重力,加速度为g且竖直向下,故C错误,D正确。在v t图像中,图线的斜率表示加速度,故斜率不变,图线应是一条倾斜的直线,A、B均错误。
5.BD 0~2t0时间内,质点P一直沿着正方向运动,则t=2t0时P未回到原点,A错误;将a-t图像转化为如图所示的v-t图像,可以看出t=2t0时,P的运动速度最小,B正确;t=3t0时,P 到原点的距离最远,C错误;t=t0时P的运动速度与t=t0时的相同,D正确。
6.BC 甲、乙t=0时刻经过同一位置,t0前能再次相遇,说明t0前存在位移相等的时刻,反映到x-t图像中就是图线有交点,反映到v-t图像中就是图线与时间轴围成的面积相等。A项图中,在t0时刻之前甲、乙位移没有相等的时刻,即两人在t0时刻之前不能相遇,A不符合题意;B项图中,在t0时刻之前图线有交点(同一时间到达同一位置),即在交点对应的时刻甲、乙两人位移相等,即两人在t0时刻之前能再次相遇,B符合题意;v-t图像与横轴围成的面积表示位移,C项图中,甲、乙在t0时刻之前位移有相等的时刻,即两人能再次相遇,C符合题意;由D项图像可知在t0时刻之前,甲的位移始终大于乙的位移,则两人不能相遇,D不符合题意。
7.答案 (1)24.00 80.0 (2)见解析
(3)70.6(70.0~71.2均正确) 59.0 (4)b 2k
解析 (1)由纸带上的数据可得ΔxAD=6.60 cm+8.00 cm+9.40 cm=24.00 cm,平均速度=80.0 cm/s。
(2)描点连线,作出的图像如图所示。
(3)=kΔt+b中k表示图线斜率,b表示图线纵截距,由-Δt图线可得k≈70.6 cm/s2,b=59.0 cm/s。
(4)由=kΔt+b得Δx=k(Δt)2+bΔt,对比x=at2+v0t,可得初速度vA=b,加速度a=2k。
高考风向 利用打点计时器测量速度、加速度是高考的常考内容,如2023年浙江1月选考第16题Ⅰ、2022年北京卷第16题等,都考查了此类问题。一般以物体做直线运动来设计学习探索问题情境,考查学生分析打点计时器所打纸带的计数点间距离和小车位移、所用时间和平均速度大小的关系,在此基础上总结实验规律并求出相关的物理量。要用到的物理知识有:某段时间内中间时刻的瞬时速度用这段时间内的平均速度来表示、用逐差法计算加速度、图像法的利用等。
8.答案 ① ③偶然
解析 ①匀变速直线运动中,中间时刻速度等于平均速度,所以小球在位置1的速度为v1=
②题中要求充分利用数据,利用逐差法求解加速度,则x4-x1=3a1T2,x5-x2=3a2T2,x6-x3=3a3T2,解得加速度为a=
③读数产生的误差是人为因素造成的,属于偶然误差。
三年模拟练
1.C 2.D 3.AC 4.BC
1.C 在v-t图像中,图线的斜率表示加速度,由图可知,甲同学先做加速度减小的加速运动后做匀速运动,A错误。在v-t图像中图线与横轴所围的面积表示位移,甲、乙两个同学从同一起跑线同时起跑,t1时间内,甲运动的位移大于乙运动的位移,故t1时刻甲同学在乙同学前面;阴影Ⅰ的面积表示t1时间内甲比乙多运动的距离,阴影Ⅱ的面积表示t1到t2时间内乙比甲多运动的距离,由于阴影Ⅰ的面积大于阴影Ⅱ的面积,因此在t2时间内甲同学运动的位移大于乙同学运动的位移,所以在t2时刻甲同学在乙同学前面,B错误,C正确;t2时刻后乙的速度大于甲的速度,所以后50 m乙同学有可能超过甲同学先到达终点,D错误。
2.D 若A不变,有两种情况,第一种情况是A>0,相等位移内速度增加量相等,平均速度越来越大,所以相等位移内用的时间越来越短,由a=可知,a越来越大;第二种情况是A<0,在这种情况下,相等位移内速度减少量相等,平均速度越来越小,所以相等位移内用的时间越来越长,由a=可知,a越来越小,A、B错误;若A不变,即相等位移内速度变化量相等,所以通过前半段位移过程中,速度变化量为,所以中间位置的速度为,C错误,D正确。
3.AC
关键点拨
滚瓶做末速度为零的匀减速直线运动,采用逆向思维,利用等位移的运动规律求解。
设滚瓶依次经过A、B、C、D、E两相邻位置的时间间隔分别为t1、t2、t3和t4,根据逆向思维可知t4∶t3∶t2∶t1=1∶(-1)∶()∶(2-),而t4=1 s,故滚瓶由位置A到E所用的时间t=t4+t3+t2+t1=2 s,即滚瓶从A到E的时间是从D到E的时间的2倍,A正确。根据v2=2ax可知滚瓶在各点的速度比满足vA∶vB∶vC∶vD=2∶∶1,B错误。滚瓶由位置D到E,由x=可得a=0.4 m/s2,C正确。滚瓶从O点到位置E,有xOE= m=1.25 m,所以xOA=0.45 m,xOB=0.65 m,xOC=0.85 m,xOD=1.05 m;若以0.9 m/s的速度将滚瓶推出,滚瓶运动的位移为x'= m=1.012 5 m,xOC
5.答案 (1)4 s (2)168 m (3)56 s
解析 (1)每一辆车做一次匀加速运动和一次匀减速运动的时间均相等,设为Δt,则有aΔt2,可得Δt=2 s
设第二辆车从启动至车头到达收费窗口停车线经过的时间为t1,则有t1=2Δt=4 s
(2)设小华从开始刹车到刚好停止的时间为t2,运动的位移大小为x1,则有t2==10 s
x1=t2=75 m
此时车头到收费窗口停车线的距离为d1=3(L+L0)=18 m
离开后汽车加速到v0,运动的位移大小x2=x1=75 m
位置A、B间的距离x3=x1+d1+x2=168 m
(3)小华在国庆节前从位置A到位置B运动的v-t图像如图所示:
从位置A到位置B的时间t3=2t2+4t0+3×2Δt=72 s
小华在国庆节期间从位置A到位置B运动的v-t图像如图所示:
速度从v0减到v的时间t4==6 s,位移大小x4=t4=63 m
匀速运动至停车线所用时间t5==2 s
汽车速度恢复到v0的时间t6=t4=6 s
故节约的时间Δt'=t3-(t4+t5+t6+)
可得Δt'=56 s。
6.答案 (1)加速度逐渐增大的减速运动
(2)6 m/s (3)见解析
解析 (1)由图2可知汽车制动过程,其加速度a随位移x均匀增大,汽车做加速度逐渐增大的减速运动。
(2)由匀变速直线运动的速度与位移的关系可得v2-=-2ax
汽车做非匀变速直线运动,运用“微元法”,可知“a-x”图线与x轴所围图形的“面积”即“速度平方变化量的一半”(破题关键),即 m2·s-2
解得v0=6 m/s
(3)该同学的做法不正确;汽车以大小为3 m/s2的加速度做匀减速运动时,v-t图像如图中直线所示;位移不变,即v-t图线与t轴围成的面积不变;由a-x图像可知,加速度随位移均匀增大,对应的v-t图线如图中曲线所示,可得实际制动时间一定小于2 s。
知识迁移 本题涉及微元法,将课本中“v-t”图线与t轴所围图形的“面积”表示物体的位移的方法进行知识迁移,得出“a-x”图线与x轴所围图形的“面积”的物理意义,从而得出汽车的初速度大小。由此可见,运用合适的物理方法,巧妙利用图像处理物理问题在物理学习中特别重要。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
