2024年齐齐哈尔地区中考数学预测卷(八)(含解析)
文档属性
| 名称 | 2024年齐齐哈尔地区中考数学预测卷(八)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-19 15:05:41 | ||
图片预览




文档简介
2024年齐齐哈尔地区中考数学预测卷(八)
学校:___________姓名:___________班级:___________考号:___________
时间:120分钟 满分:120分
一、单选题(共10小题,每小题3分,共计30分)
1.的绝对值是( )
A. B. C. D.
2.(2024·四川内江·中考真题)2024年6月5日,是二十四节气的芒种,二十四节气是中国劳动人民独创的文化遗产,能反映季节的变化,指导农事活动.下面四副图片分别代表“芒种”、“白露”、“立夏”、“大雪”,其中是中心对称图形的是( )
A. B. C. D.
3.(2024·四川广安·中考真题)下列运算中,正确的是( )
A. B. C. D.
4.由相同的小正方体搭成的立体图形的部分视图如图所示,则搭成该立体图形的小正方体的最少个数为( )
A.6 B.9 C.10 D.14
5.随着科技发展,骑行共享单车这种“低碳”生活方式已融人人们的日常生活.如图是共享单车车架的示意图,线段分别为前叉、下管和立管(点C在上),为后下叉.已知,,则的度数为( )
A. B. C. D.
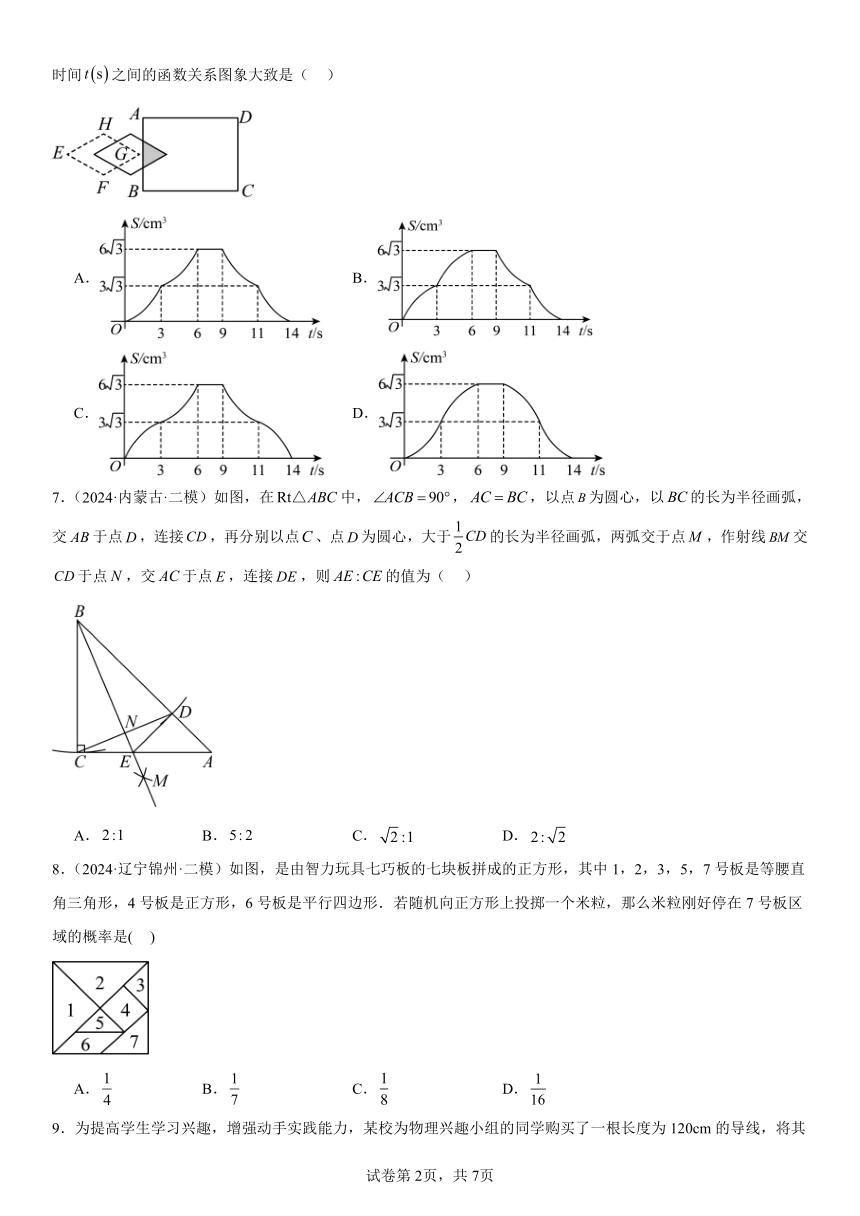
6.(2024·山东烟台·中考真题)如图,水平放置的矩形中,,,菱形的顶点,在同一水平线上,点与的中点重合,,,现将菱形以的速度沿方向匀速运动,当点运动到上时停止,在这个运动过程中,菱形与矩形重叠部分的面积与运动时间之间的函数关系图象大致是( )
A. B.
C. D.
7.(2024·内蒙古·二模)如图,在中,,,以点为圆心,以的长为半径画弧,交于点,连接,再分别以点、点为圆心,大于的长为半径画弧,两弧交于点,作射线交于点,交于点,连接,则的值为( )
A. B. C. D.
8.(2024·辽宁锦州·二模)如图,是由智力玩具七巧板的七块板拼成的正方形,其中1,2,3,5,7号板是等腰直角三角形,4号板是正方形,6号板是平行四边形.若随机向正方形上投掷一个米粒,那么米粒刚好停在7号板区域的概率是( )
A. B. C. D.
9.为提高学生学习兴趣,增强动手实践能力,某校为物理兴趣小组的同学购买了一根长度为120cm的导线,将其全部截成和两种长度的导线(每种长度的导线至少一根)用于实验操作,则截取方案共有( )
A.8 种 B.7种 C.6种 D.5种
10.(2024·四川遂宁·中考真题)如图,已知抛物线(a、b、c为常数,且)的对称轴为直线,且该抛物线与轴交于点,与轴的交点在,之间(不含端点),则下列结论正确的有多少个( )
①;
②;
③;
④若方程两根为,则.
A.1 B.2 C.3 D.4
二、填空题(共7小题,每小题3分,共计21分)
11.(2024·山东德州·二模)华为手机使用了自主研发的海思麒麟芯片,目前最新的型号是麒麟990.芯片是由很多晶体管组成的,而芯片技术追求是体积更小的晶体管,以便获得更小的芯片和更低的电力功耗,而麒麟990的晶体管栅极的宽度达到了0.000000007毫米,将数据0.000000007用科学记数法表示为 .
12.(2023·四川巴中·模拟预测)在函数中,自变量的取值范围是 .
13.(2024·陕西渭南·二模)如图,在和中,点D在上,,,请你再添加一个条件:______,使得,并说明理由.
14.(2024·云南昭通·二模)某盏路灯照射的空间可以看成如图所示的圆锥,它的高米,母线与底面半径的夹角为α,,则圆锥的侧面积是 平方米.(结果保留π)
15.关于的分式方程无解,则的值为 .
16.在中,的平分线交边于点E,于点M,N是的中点,连接.若,,,则的长度为 .
17.(2024·四川广安·中考真题)已知,直线与轴相交于点,以为边作等边三角形,点在第一象限内,过点作轴的平行线与直线交于点,与轴交于点,以为边作等边三角形(点在点的上方),以同样的方式依次作等边三角形,等边三角形,则点的横坐标为 .
三、解答题(共7小题,共计69分)
18.(1)(2024·湖南长沙·二模)(6分)计算:.
(2)(4分)因式分解:
19.(5分)解方程:(2).
20.(2024·江苏无锡·二模)(8分)我校举办了校园文创设计大赛,并从七年级学生中随机抽取部分学生进行问卷调查,要求每名学生从4个获奖作品中选择一个自己最喜欢的作品,根据调查结果绘制成如图所示的两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)参加此次问卷调查的学生人数是_______,并将条形统计图补充完整;
(2)在扇形统计图中,选择“作品1”的学生所对应扇形的圆心角的度数是_______;
(3)若我校七年级学生共有500名,请估计七年级学生中选择“作品3”的人数.
21.(2022·内蒙古鄂尔多斯·中考真题)(10分)如图,以AB为直径的⊙O与△ABC的边BC相切于点B,且与AC边交于点D,点E为BC中点,连接DE、BD.
(1)求证:DE是⊙O的切线;
(2)若DE=5,cos∠ABD=,求OE的长.
22.(10分)甲、乙两车分别从,两地同时出发,匀速行驶,先相向而行.途中乙车因故停留小时,然后以原速继续向地行驶,甲车到达地后,立即按原路原速返回地(甲车掉头的时间忽略不计),到达地后停止行驶,原地休息;甲、乙两车距地的路程(千米)与所用时间(时)之间的函数图象如图,请结合图象信息解答下列问题:
(1)乙车的速度为 千米/时,在图中的( )内应填上的数是 .
(2)求甲车从地返回地的过程中,与的函数关系式.
(3)两车出发后几小时相距千米,请直接写出答案: 时.
23.(2024·湖北恩施·三模)综合与探究(12分)
问题背景:如图3,四边形是矩形,,点G、H、E分别是线段、、上的动点,连接,过点E作的垂线交线段于点F(只考虑F在上的情况)
(1)①如图1,当点G运动到A点,点E运动到B点时,若,,,则的值为______(直接写答案)
②如图2,当点G不与A点重合,点E运动到B点时,若,试求的值.
问题探究:
(2)如图3,当G不与A重合,E不与B重合时,用含m的式子表示的值.
问题拓展:
(3)如图4,将背景问题中的矩形改成已知“在四边形中,,,,,则的值为______.(直接写答案)
24.(2023·贵州遵义·模拟预测)(14分)如图,抛物线(、为常数)与轴交于、两点,与轴交于点,直线的函数关系式为.
(1)求该抛物线的函数关系式与点坐标;
(2)已知点是线段上的一个动点,过点作轴的垂线分别与直线和抛物线交于、两点,当为何值时,恰好是以为底边的等腰三角形?
(3)在(2)问条件下,当恰好是以为底边的等腰三角形时,动点相应位置记为点,将绕原点顺时针旋转得到(旋转角在到之间);
①探究:线段上是否存在定点(不与、重合),无论如何旋转,始终保持不变,若存在,试求出点坐标;若不存在,请说明理由;
②试求出此旋转过程中,的最小值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】本题考查了绝对值.根据绝对值的性质可得答案.正数的绝对值等于它本身,负数的绝对值等于它的相反数,0的绝对值等于0.
【详解】解:的绝对值是.
故选:D.
2.D
【分析】根据中心对称图形的定义:把一个图形绕着某一个点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心,进行逐一判断即可.本题主要考查了中心对称图形,解题的关键在于能够熟练掌握中心对称图形的定义.
【详解】解:A.不是中心对称图形,故A选项不合题意;
B.不是中心对称图形,故B选项不合题意;
C.不是中心对称图形,故C选项不合题意;
D.是中心对称图形,故D选项合题意;
故选:D.
3.B
【分析】本题考查整式的运算,根据合并同类项法则、积的乘方运算法则、完全平方公式和同底数幂的除法运算法则逐项判断即可解答.
【详解】解:A、和不是同类项,不能加减,故原计算错误,不符合题意;
B、,计算正确,符合题意;
C、,故原计算错误,不符合题意;
D、,故原计算错误,不符合题意;
故选:B.
4.B
【分析】本题考查了由三视图判断小立方体的个数.根据俯视图可得底层最少有6个,再结合主视图可得第二层最少有2个,即可解答.
【详解】解:根据俯视图可得搭成该立体图形的小正方体底层最少为6个,
根据主视图可得第二层最少为2个,
根据主视图可得第三层最少为1个,
故搭成该立体图形的小正方体最少为个,
故选:B.
5.D
【分析】本题考查平行线的性质,关键是由平行线的性质推出.
由平行线的性质推出,求出.即可得到的度数.
【详解】解:∵,
,
,
,
,
,
故选:D.
6.D
【分析】本题考查了解直角三角形的应用,菱形的性质,动点问题的函数图象,二次函数的图象的性质,先求得菱形的面积为,进而分三种情形讨论,重合部分为三角形,重合部分为五边形,重合部分为菱形,分别求得面积与运动时间的函数关系式,结合选项,即可求解.
【详解】解:如图所示,设交于点,
∵菱形,,
∴
又∵,
∴是等边三角形,
∵,,
∴
∴
∴
当时,重合部分为,
如图所示,
依题意,为等边三角形,
运动时间为,则,
∴
当时,如图所示,
依题意,,则
∴
∴
∵
∴当时,
当时,同理可得,
当时,同理可得,
综上所述,当时,函数图象为开口向上的一段抛物线,当时,函数图象为开口向下的一段抛物线,当时,函数图象为一条线段,当时,函数图象为开口向下的一段抛物线,当时,函数图象为开口向上的一段抛物线;
故选:D.
7.C
【分析】本题考查基本作图,等腰直角三角形的性质及勾股定理应用等知识,根据尺规作图可得,是的平分线,可证明得,根据直角三角形的性质可得,可推出,进而求出结论.
【详解】解:由尺规作图可得,是的平分线,,
∴,
∵,
∴,
∴,
在中,,
∴,
在中,,
,
∴,
故选:C.
8.C
【分析】本题考查几何概型概率的求法,勾股定理,正方形的性质;设号板正方形的边长为,则号板直角边长为,号板斜边长为,号板斜边长为,直角边长为,则大正方形边长为,据此知大正方形的面积为,号板的面积为,再根据概率公式求解可得.
【详解】解:设号板正方形的边长为,则号板直角边长为,号板斜边长为,
号板斜边长为,直角边长为,则大正方形边长为,
号板的面积为,
大正方形的面积为,
从这个正方形内任取一点,则刚好停在号板区域的概率是,
故选:C.
9.B
【分析】本题考查了二元一次方程的应用.设和两种长度的导线分别为根,根据题意,得出,进而根据为正整数,即可求解.
【详解】解:设和两种长度的导线分别为根,根据题意得,
,
即,
∵为正整数,
∴,3,5,7,9,11,13,
则,6,5,4,3,2,1,
故有7种方案,
故选:B.
10.B
【分析】本题主要考查二次函数和一次函数的性质,根据题干可得,,,即可判断①错误;根据对称轴和一个交点求得另一个交点为,即可判断②错误;将c和b用a表示,即可得到,即可判断③正确;结合抛物线和直线与轴得交点,即可判断④正确.
【详解】解:由图可知,
∵抛物线的对称轴为直线,且该抛物线与轴交于点,
∴,,
则,
∵抛物线与轴的交点在,之间,
∴,
则,故①错误;
设抛物线与轴另一个交点,
∵对称轴为直线,且该抛物线与轴交于点,
∴,解得,
则,故②错误;
∵,,,
∴,解得,故③正确;
根据抛物线与轴交于点和,直线过点和,如图,
方程两根为满足,故④正确;
故选:B.
11.
【分析】本题考查了科学记数法的表示方法.根据科学记数法的表示形式为的形式,其中为整数,表示时关键要正确确定a的值以及n的值.
【详解】解:将数据0.000000007用科学记数法表示为,
故答案为:.
12.且
【分析】本题考查了函数自变量的取值范围的确定,根据二次根式,分式有意义的条件及非零指数幂列出不等式,解不等式即可求解,熟练掌握二次根式,分式有意义的条件及非零指数幂的概念是解题的关键.
【详解】解:由题意得,且
∴且,
故答案为:且.
13.,理由见解析
【分析】本题考查了三角形全等的判定条件,判定三角形全等的定理有:,熟练掌握三角形全等的判定定理是解题的关键.
根据已知条件可推知,两个三角形有一组角、一组边分别对应相等,只需要再添加一组对应角相等,构成或即可证得两三角形全等(也可添加条件,构成).
【详解】解:添加的条件是:.
理由:∵,
∴,即.
在和中,,,,
∴.
注:答案不唯一,添加或均可.
14.
【分析】本题考查求圆锥的侧面积,解直角三角形,根据三角函数求出和的长,再利用圆锥的侧面积公式进行求解即可.
【详解】解:在中,,,
∴,
∴,
∴圆锥的侧面积;
故答案为:.
15.或
【分析】本题考查了解分式方程无解的情况,先将分式方程去分母,化为整式方程,再分和两种情况解答即可求解,理解分式方程无解的意义是解题的关键.
【详解】解:方程两边同乘以得,,
整理的,,
当,即时,方程无解;
当,即时,,
∵方程无解,
∴是方程的增根,
∴,
解得;
∴的值为或,
故答案为:或.
16.或
【分析】根据题意画出示意图,当点G在线段上时,延长交于点F,连接过点B作于点G,过点A作于点H,证明,进而证明四边形是菱形,得到,点M是的中点,由N是的中点,易得是的中位线,从而得到,,再根据,利用勾股定理,利用勾股定理求出,从而得到,由三角形面积公式,求出,由等腰三角形的性质得到,从而得到,利用勾股定理即可求出的长;当点G在延长线上时,同理进行解答即可.
【详解】解;如图,当点G在线段上时,延长交于点F,连接过点B作于点G,过点A作于点H,
在中,,
四边形是平行四边形,
是的平分线,,
,,
,
,
,
,
四边形是菱形,
,点M是的中点,
N是的中点,
是的中位线,
,
,
,,
,
,
(负值舍去),
,
,
,
,
,
,
;
如图,当点G在延长线上时,
同理,得到,
,
,
,
,
,
,
;
综上,的长度为或.
【点睛】本题考查平行四边形的性质,菱形的判定与性质,等腰直角三角形的性质,勾股定理,三角形面积公式,根据题意画出示意图并正确作出辅助线是解题的关键.
17.
【分析】直线直线可知,点坐标为,可得,由于是等边三角形,可得点,把代入直线解析式即可求得的横坐标,可得,由于是等边三角形,可得点;同理,,发现规律即可得解,准确发现坐标与字母的序号之间的规律是解题的关键.
【详解】解:∵直线l:与x轴负半轴交于点,
∴点坐标为,
∴,
过,,作轴交x轴于点M,轴交于点D,交x轴于点N,
∵为等边三角形,
∴
∴,
∴
∴,
当时,,解得:,
∴,,
∴,
∴,
∴,
∴当时,,解得:,
∴;
而,
同理可得:的横坐标为,
∴点的横坐标为,
故答案为:.
【点睛】本题主要考查了一次函数图象上点的坐标的特征,勾股定理的应用,等边三角形的性质,特殊图形点的坐标的规律,掌握探究的方法是解本题的关键.
18.(1)0;(2)
【详解】(1)
.
(2)解:原式
.
19.
【详解】,
整理得:,
∴,
或,
.
20.(1)50,图见解析
(2)
(3)180名
【分析】本题考查了条形统计图与扇形统计图信息相关联,求扇形统计图中圆心角的度数,用样本估计总体的数量等知识;善于从统计图中获取相关信息是解题的关键.
(1)根据喜欢作品4的人数及所占的百分比即可求得调查的人数,则可求得喜欢作品2的人数,进而补充完整条形统计图;
(2)根据喜欢作品1所占的百分比与周角的乘积即可求得圆心角的度数;
(3)喜欢作品3所上占的百分比与全校七年级学生人数的乘积,即是估计喜欢作品3的人数.
【详解】(1)解:参加调查问卷的学生人数为:(名);
喜欢作品2的人数为:(名),
补充后的条形统计图如下:
故答案为:50;
(2)解:;
故答案为:;
(3)解:(名)
答:估计七年级学生中选择作品3的有180名.
21.(1)见解析
(2)
【分析】(1)连接OD,可推出∠BDC=90°,进而得出DE=BE,然后证明△DOE≌△BOE,求出∠ODE=∠ABC=90°即可得出结论;
(2 )可推出∠C=∠ABD,解直角△ABC求得AC,进而根据三角形中位线定理求得OE.
【详解】(1)证明:如图,连接OD,
∵AB为⊙O的直径,BC为⊙O的切线,
∴∠BDC=∠ADB=90°,∠ABC=90°,
∵E是BC的中点,
∴DE=BE=EC=,
在△DOE和△BOE中,,
∴△DOE≌△BOE(SSS),
∴∠ODE=∠ABC=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)解:∵∠ABC=90°,
∴∠ABD+∠CBD=90°,
由(1)知:∠BDC=90°,BC=2DE,
∴∠C+∠DBC=90°,BC=2DE=10,
∴∠C=∠ABD,
在Rt△ABC中,AC==,
∵OA=OB,BE=CE,
∴OE=.
【点睛】本题考查了切线的判定和性质,直角三角形斜边中线的性质,全等三角形的判定和性质,解直角三角形,三角形中位线定理等知识,解决问题的关键是灵活运用有关基础知识.
22.(1),;
(2)与的函数解析式为;
(3)或或.
【分析】()结合函数图象,根据行程问题的数量关系:速度=路程时间,路程速度时间就可以求解;
()由()的结论可以求出点的坐标,再由题意可得点的坐标,由待定系数法求出的解析式;
()分当两车第一次相遇前相距千米的路程;当两车第一次相遇后,甲车到达地前,相距千米的路程;当甲车到达地后返回地,两车第二次相遇后,甲车到地距离共有千米,所以两车不可能再相距千米;分别求解即可.
【详解】(1)由函数图象可得:,两地相距路程是千米,
乙车行驶的速度是(千米/时),
图中括号内的数为:,
故答案为:,;
(2),甲车的速度为千米/时,
甲车从地到地需(小时),故点坐标,
设甲车从地返回地过程中与的函数解析式为,
将,代入上式,得
,
解得,
∴与的函数解析式为;
(3)设两车出发后小时相距千米的路程,
当两车第一次相遇前相距千米的路程,根据题意,得
,
解得:,
当两车第一次相遇后,甲车到达地前,相距千米的路程,根据题意,得
,
解得:,
当甲车到达地后返回甲地,两车第二次相遇时相距千米的路程,
∵,
∴乙在停留时两车第二次相遇时相距120千米,
根据题意,得,
解得:,
当甲车到达地后返回地,两车第二次相遇后,甲车到地距离共有千米,所以两车不可能再相距千米;
综上,两车出发后小时或小时或小时相距千米的路程.
故答案为:2或或.
【点睛】此题考查了待定系数法求一次函数的解析式,函数图象,一次函数与一元一次方程的运用,解答时从函数图象获取信息是解题的关键.
23.(1)①2;②2;(2);(3).
【分析】(1)①如图, 证明,可得,结合,,,从而可得答案;②如图,过作交于, 而,可得,再利用①的结论即可;
(2)如图,过作交于, 而,可得,同理可得:,过作交于,同理可得:四边形为平行四边形,可得,,结合①可得答案;
(3)如图,过作的平行线交的延长线于,过作的垂线交于,而,证明四边形为矩形,,设,则,求解,再结合(1)的结论可得答案.
【详解】解:(1)①如图,
∵矩形,
∴,
∴,
∵,
∴,
∴,
∴,
∴
∵,,,
∴,
∴;
②如图,过作交于, 而
∴,
∵矩形,
∴,
∴四边形是平行四边形,
∴,
由①可得:,
∴;
(2)如图,过作交于, 而
∴,
同理可得:,
过作交于,
同理可得:四边形为平行四边形,
∴,,
由①可得:,
∴;
(3)如图,过作的平行线交的延长线于,过作的垂线交于,而,
∴,,,
∴四边形为矩形,
∴,
∵,
∴,
设,则,
∵,
∴,
∵,
结合(1)的结论可得:.
【点睛】本题考查的是矩形的判定与性质,平行四边形的判定与性质,相似三角形的判定与性质,锐角三角函数的应用,熟练的利用类比的数学方法解题是关键.
24.(1),
(2)
(3)①存在,;②
【分析】(1)先求出,再运用待定系数法求出抛物线的函数关系式,即,再令,解出,即可作答.
(2)先表达,结合“恰好是以为底边的等腰三角形”得出,代入数值,运用因式分解法解方程,即可作答.
(3)①证明,根据,得出不变,则,即可作答.②在以为圆心,4为半径的半圆上,,结合运动轨迹,得出的最小值,再运用勾股定理列式计算,即可作答.
【详解】(1)解:在中,
令,则,
令,则,
,
把代入
得,
,
抛物线的函数关系式为:,
令,则,
,
;
(2)解:点,过点作轴的垂线分别与直线和抛物线交于、两点,
,
当为底时,作于,
则,
,
,
解得:(不合题意,舍去),
当时,恰好是以为底边的等腰三角形;
(3)解:①存在,,过程如下:
,
,
当时,,
不变,
即,
②将绕原点顺时针旋转得到(旋转角在到之间);
∴在以为圆心,4为半径的半圆上,
由①知,,
,
的最小值,
此时三点共线,
∵
的最小值.
【点睛】本题考查了二次函数的几何综合,解一元二次方程,相似三角形的判定与性质,勾股定理,正确掌握相关性质内容是解题的关键.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
时间:120分钟 满分:120分
一、单选题(共10小题,每小题3分,共计30分)
1.的绝对值是( )
A. B. C. D.
2.(2024·四川内江·中考真题)2024年6月5日,是二十四节气的芒种,二十四节气是中国劳动人民独创的文化遗产,能反映季节的变化,指导农事活动.下面四副图片分别代表“芒种”、“白露”、“立夏”、“大雪”,其中是中心对称图形的是( )
A. B. C. D.
3.(2024·四川广安·中考真题)下列运算中,正确的是( )
A. B. C. D.
4.由相同的小正方体搭成的立体图形的部分视图如图所示,则搭成该立体图形的小正方体的最少个数为( )
A.6 B.9 C.10 D.14
5.随着科技发展,骑行共享单车这种“低碳”生活方式已融人人们的日常生活.如图是共享单车车架的示意图,线段分别为前叉、下管和立管(点C在上),为后下叉.已知,,则的度数为( )
A. B. C. D.
6.(2024·山东烟台·中考真题)如图,水平放置的矩形中,,,菱形的顶点,在同一水平线上,点与的中点重合,,,现将菱形以的速度沿方向匀速运动,当点运动到上时停止,在这个运动过程中,菱形与矩形重叠部分的面积与运动时间之间的函数关系图象大致是( )
A. B.
C. D.
7.(2024·内蒙古·二模)如图,在中,,,以点为圆心,以的长为半径画弧,交于点,连接,再分别以点、点为圆心,大于的长为半径画弧,两弧交于点,作射线交于点,交于点,连接,则的值为( )
A. B. C. D.
8.(2024·辽宁锦州·二模)如图,是由智力玩具七巧板的七块板拼成的正方形,其中1,2,3,5,7号板是等腰直角三角形,4号板是正方形,6号板是平行四边形.若随机向正方形上投掷一个米粒,那么米粒刚好停在7号板区域的概率是( )
A. B. C. D.
9.为提高学生学习兴趣,增强动手实践能力,某校为物理兴趣小组的同学购买了一根长度为120cm的导线,将其全部截成和两种长度的导线(每种长度的导线至少一根)用于实验操作,则截取方案共有( )
A.8 种 B.7种 C.6种 D.5种
10.(2024·四川遂宁·中考真题)如图,已知抛物线(a、b、c为常数,且)的对称轴为直线,且该抛物线与轴交于点,与轴的交点在,之间(不含端点),则下列结论正确的有多少个( )
①;
②;
③;
④若方程两根为,则.
A.1 B.2 C.3 D.4
二、填空题(共7小题,每小题3分,共计21分)
11.(2024·山东德州·二模)华为手机使用了自主研发的海思麒麟芯片,目前最新的型号是麒麟990.芯片是由很多晶体管组成的,而芯片技术追求是体积更小的晶体管,以便获得更小的芯片和更低的电力功耗,而麒麟990的晶体管栅极的宽度达到了0.000000007毫米,将数据0.000000007用科学记数法表示为 .
12.(2023·四川巴中·模拟预测)在函数中,自变量的取值范围是 .
13.(2024·陕西渭南·二模)如图,在和中,点D在上,,,请你再添加一个条件:______,使得,并说明理由.
14.(2024·云南昭通·二模)某盏路灯照射的空间可以看成如图所示的圆锥,它的高米,母线与底面半径的夹角为α,,则圆锥的侧面积是 平方米.(结果保留π)
15.关于的分式方程无解,则的值为 .
16.在中,的平分线交边于点E,于点M,N是的中点,连接.若,,,则的长度为 .
17.(2024·四川广安·中考真题)已知,直线与轴相交于点,以为边作等边三角形,点在第一象限内,过点作轴的平行线与直线交于点,与轴交于点,以为边作等边三角形(点在点的上方),以同样的方式依次作等边三角形,等边三角形,则点的横坐标为 .
三、解答题(共7小题,共计69分)
18.(1)(2024·湖南长沙·二模)(6分)计算:.
(2)(4分)因式分解:
19.(5分)解方程:(2).
20.(2024·江苏无锡·二模)(8分)我校举办了校园文创设计大赛,并从七年级学生中随机抽取部分学生进行问卷调查,要求每名学生从4个获奖作品中选择一个自己最喜欢的作品,根据调查结果绘制成如图所示的两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)参加此次问卷调查的学生人数是_______,并将条形统计图补充完整;
(2)在扇形统计图中,选择“作品1”的学生所对应扇形的圆心角的度数是_______;
(3)若我校七年级学生共有500名,请估计七年级学生中选择“作品3”的人数.
21.(2022·内蒙古鄂尔多斯·中考真题)(10分)如图,以AB为直径的⊙O与△ABC的边BC相切于点B,且与AC边交于点D,点E为BC中点,连接DE、BD.
(1)求证:DE是⊙O的切线;
(2)若DE=5,cos∠ABD=,求OE的长.
22.(10分)甲、乙两车分别从,两地同时出发,匀速行驶,先相向而行.途中乙车因故停留小时,然后以原速继续向地行驶,甲车到达地后,立即按原路原速返回地(甲车掉头的时间忽略不计),到达地后停止行驶,原地休息;甲、乙两车距地的路程(千米)与所用时间(时)之间的函数图象如图,请结合图象信息解答下列问题:
(1)乙车的速度为 千米/时,在图中的( )内应填上的数是 .
(2)求甲车从地返回地的过程中,与的函数关系式.
(3)两车出发后几小时相距千米,请直接写出答案: 时.
23.(2024·湖北恩施·三模)综合与探究(12分)
问题背景:如图3,四边形是矩形,,点G、H、E分别是线段、、上的动点,连接,过点E作的垂线交线段于点F(只考虑F在上的情况)
(1)①如图1,当点G运动到A点,点E运动到B点时,若,,,则的值为______(直接写答案)
②如图2,当点G不与A点重合,点E运动到B点时,若,试求的值.
问题探究:
(2)如图3,当G不与A重合,E不与B重合时,用含m的式子表示的值.
问题拓展:
(3)如图4,将背景问题中的矩形改成已知“在四边形中,,,,,则的值为______.(直接写答案)
24.(2023·贵州遵义·模拟预测)(14分)如图,抛物线(、为常数)与轴交于、两点,与轴交于点,直线的函数关系式为.
(1)求该抛物线的函数关系式与点坐标;
(2)已知点是线段上的一个动点,过点作轴的垂线分别与直线和抛物线交于、两点,当为何值时,恰好是以为底边的等腰三角形?
(3)在(2)问条件下,当恰好是以为底边的等腰三角形时,动点相应位置记为点,将绕原点顺时针旋转得到(旋转角在到之间);
①探究:线段上是否存在定点(不与、重合),无论如何旋转,始终保持不变,若存在,试求出点坐标;若不存在,请说明理由;
②试求出此旋转过程中,的最小值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】本题考查了绝对值.根据绝对值的性质可得答案.正数的绝对值等于它本身,负数的绝对值等于它的相反数,0的绝对值等于0.
【详解】解:的绝对值是.
故选:D.
2.D
【分析】根据中心对称图形的定义:把一个图形绕着某一个点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心,进行逐一判断即可.本题主要考查了中心对称图形,解题的关键在于能够熟练掌握中心对称图形的定义.
【详解】解:A.不是中心对称图形,故A选项不合题意;
B.不是中心对称图形,故B选项不合题意;
C.不是中心对称图形,故C选项不合题意;
D.是中心对称图形,故D选项合题意;
故选:D.
3.B
【分析】本题考查整式的运算,根据合并同类项法则、积的乘方运算法则、完全平方公式和同底数幂的除法运算法则逐项判断即可解答.
【详解】解:A、和不是同类项,不能加减,故原计算错误,不符合题意;
B、,计算正确,符合题意;
C、,故原计算错误,不符合题意;
D、,故原计算错误,不符合题意;
故选:B.
4.B
【分析】本题考查了由三视图判断小立方体的个数.根据俯视图可得底层最少有6个,再结合主视图可得第二层最少有2个,即可解答.
【详解】解:根据俯视图可得搭成该立体图形的小正方体底层最少为6个,
根据主视图可得第二层最少为2个,
根据主视图可得第三层最少为1个,
故搭成该立体图形的小正方体最少为个,
故选:B.
5.D
【分析】本题考查平行线的性质,关键是由平行线的性质推出.
由平行线的性质推出,求出.即可得到的度数.
【详解】解:∵,
,
,
,
,
,
故选:D.
6.D
【分析】本题考查了解直角三角形的应用,菱形的性质,动点问题的函数图象,二次函数的图象的性质,先求得菱形的面积为,进而分三种情形讨论,重合部分为三角形,重合部分为五边形,重合部分为菱形,分别求得面积与运动时间的函数关系式,结合选项,即可求解.
【详解】解:如图所示,设交于点,
∵菱形,,
∴
又∵,
∴是等边三角形,
∵,,
∴
∴
∴
当时,重合部分为,
如图所示,
依题意,为等边三角形,
运动时间为,则,
∴
当时,如图所示,
依题意,,则
∴
∴
∵
∴当时,
当时,同理可得,
当时,同理可得,
综上所述,当时,函数图象为开口向上的一段抛物线,当时,函数图象为开口向下的一段抛物线,当时,函数图象为一条线段,当时,函数图象为开口向下的一段抛物线,当时,函数图象为开口向上的一段抛物线;
故选:D.
7.C
【分析】本题考查基本作图,等腰直角三角形的性质及勾股定理应用等知识,根据尺规作图可得,是的平分线,可证明得,根据直角三角形的性质可得,可推出,进而求出结论.
【详解】解:由尺规作图可得,是的平分线,,
∴,
∵,
∴,
∴,
在中,,
∴,
在中,,
,
∴,
故选:C.
8.C
【分析】本题考查几何概型概率的求法,勾股定理,正方形的性质;设号板正方形的边长为,则号板直角边长为,号板斜边长为,号板斜边长为,直角边长为,则大正方形边长为,据此知大正方形的面积为,号板的面积为,再根据概率公式求解可得.
【详解】解:设号板正方形的边长为,则号板直角边长为,号板斜边长为,
号板斜边长为,直角边长为,则大正方形边长为,
号板的面积为,
大正方形的面积为,
从这个正方形内任取一点,则刚好停在号板区域的概率是,
故选:C.
9.B
【分析】本题考查了二元一次方程的应用.设和两种长度的导线分别为根,根据题意,得出,进而根据为正整数,即可求解.
【详解】解:设和两种长度的导线分别为根,根据题意得,
,
即,
∵为正整数,
∴,3,5,7,9,11,13,
则,6,5,4,3,2,1,
故有7种方案,
故选:B.
10.B
【分析】本题主要考查二次函数和一次函数的性质,根据题干可得,,,即可判断①错误;根据对称轴和一个交点求得另一个交点为,即可判断②错误;将c和b用a表示,即可得到,即可判断③正确;结合抛物线和直线与轴得交点,即可判断④正确.
【详解】解:由图可知,
∵抛物线的对称轴为直线,且该抛物线与轴交于点,
∴,,
则,
∵抛物线与轴的交点在,之间,
∴,
则,故①错误;
设抛物线与轴另一个交点,
∵对称轴为直线,且该抛物线与轴交于点,
∴,解得,
则,故②错误;
∵,,,
∴,解得,故③正确;
根据抛物线与轴交于点和,直线过点和,如图,
方程两根为满足,故④正确;
故选:B.
11.
【分析】本题考查了科学记数法的表示方法.根据科学记数法的表示形式为的形式,其中为整数,表示时关键要正确确定a的值以及n的值.
【详解】解:将数据0.000000007用科学记数法表示为,
故答案为:.
12.且
【分析】本题考查了函数自变量的取值范围的确定,根据二次根式,分式有意义的条件及非零指数幂列出不等式,解不等式即可求解,熟练掌握二次根式,分式有意义的条件及非零指数幂的概念是解题的关键.
【详解】解:由题意得,且
∴且,
故答案为:且.
13.,理由见解析
【分析】本题考查了三角形全等的判定条件,判定三角形全等的定理有:,熟练掌握三角形全等的判定定理是解题的关键.
根据已知条件可推知,两个三角形有一组角、一组边分别对应相等,只需要再添加一组对应角相等,构成或即可证得两三角形全等(也可添加条件,构成).
【详解】解:添加的条件是:.
理由:∵,
∴,即.
在和中,,,,
∴.
注:答案不唯一,添加或均可.
14.
【分析】本题考查求圆锥的侧面积,解直角三角形,根据三角函数求出和的长,再利用圆锥的侧面积公式进行求解即可.
【详解】解:在中,,,
∴,
∴,
∴圆锥的侧面积;
故答案为:.
15.或
【分析】本题考查了解分式方程无解的情况,先将分式方程去分母,化为整式方程,再分和两种情况解答即可求解,理解分式方程无解的意义是解题的关键.
【详解】解:方程两边同乘以得,,
整理的,,
当,即时,方程无解;
当,即时,,
∵方程无解,
∴是方程的增根,
∴,
解得;
∴的值为或,
故答案为:或.
16.或
【分析】根据题意画出示意图,当点G在线段上时,延长交于点F,连接过点B作于点G,过点A作于点H,证明,进而证明四边形是菱形,得到,点M是的中点,由N是的中点,易得是的中位线,从而得到,,再根据,利用勾股定理,利用勾股定理求出,从而得到,由三角形面积公式,求出,由等腰三角形的性质得到,从而得到,利用勾股定理即可求出的长;当点G在延长线上时,同理进行解答即可.
【详解】解;如图,当点G在线段上时,延长交于点F,连接过点B作于点G,过点A作于点H,
在中,,
四边形是平行四边形,
是的平分线,,
,,
,
,
,
,
四边形是菱形,
,点M是的中点,
N是的中点,
是的中位线,
,
,
,,
,
,
(负值舍去),
,
,
,
,
,
,
;
如图,当点G在延长线上时,
同理,得到,
,
,
,
,
,
,
;
综上,的长度为或.
【点睛】本题考查平行四边形的性质,菱形的判定与性质,等腰直角三角形的性质,勾股定理,三角形面积公式,根据题意画出示意图并正确作出辅助线是解题的关键.
17.
【分析】直线直线可知,点坐标为,可得,由于是等边三角形,可得点,把代入直线解析式即可求得的横坐标,可得,由于是等边三角形,可得点;同理,,发现规律即可得解,准确发现坐标与字母的序号之间的规律是解题的关键.
【详解】解:∵直线l:与x轴负半轴交于点,
∴点坐标为,
∴,
过,,作轴交x轴于点M,轴交于点D,交x轴于点N,
∵为等边三角形,
∴
∴,
∴
∴,
当时,,解得:,
∴,,
∴,
∴,
∴,
∴当时,,解得:,
∴;
而,
同理可得:的横坐标为,
∴点的横坐标为,
故答案为:.
【点睛】本题主要考查了一次函数图象上点的坐标的特征,勾股定理的应用,等边三角形的性质,特殊图形点的坐标的规律,掌握探究的方法是解本题的关键.
18.(1)0;(2)
【详解】(1)
.
(2)解:原式
.
19.
【详解】,
整理得:,
∴,
或,
.
20.(1)50,图见解析
(2)
(3)180名
【分析】本题考查了条形统计图与扇形统计图信息相关联,求扇形统计图中圆心角的度数,用样本估计总体的数量等知识;善于从统计图中获取相关信息是解题的关键.
(1)根据喜欢作品4的人数及所占的百分比即可求得调查的人数,则可求得喜欢作品2的人数,进而补充完整条形统计图;
(2)根据喜欢作品1所占的百分比与周角的乘积即可求得圆心角的度数;
(3)喜欢作品3所上占的百分比与全校七年级学生人数的乘积,即是估计喜欢作品3的人数.
【详解】(1)解:参加调查问卷的学生人数为:(名);
喜欢作品2的人数为:(名),
补充后的条形统计图如下:
故答案为:50;
(2)解:;
故答案为:;
(3)解:(名)
答:估计七年级学生中选择作品3的有180名.
21.(1)见解析
(2)
【分析】(1)连接OD,可推出∠BDC=90°,进而得出DE=BE,然后证明△DOE≌△BOE,求出∠ODE=∠ABC=90°即可得出结论;
(2 )可推出∠C=∠ABD,解直角△ABC求得AC,进而根据三角形中位线定理求得OE.
【详解】(1)证明:如图,连接OD,
∵AB为⊙O的直径,BC为⊙O的切线,
∴∠BDC=∠ADB=90°,∠ABC=90°,
∵E是BC的中点,
∴DE=BE=EC=,
在△DOE和△BOE中,,
∴△DOE≌△BOE(SSS),
∴∠ODE=∠ABC=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)解:∵∠ABC=90°,
∴∠ABD+∠CBD=90°,
由(1)知:∠BDC=90°,BC=2DE,
∴∠C+∠DBC=90°,BC=2DE=10,
∴∠C=∠ABD,
在Rt△ABC中,AC==,
∵OA=OB,BE=CE,
∴OE=.
【点睛】本题考查了切线的判定和性质,直角三角形斜边中线的性质,全等三角形的判定和性质,解直角三角形,三角形中位线定理等知识,解决问题的关键是灵活运用有关基础知识.
22.(1),;
(2)与的函数解析式为;
(3)或或.
【分析】()结合函数图象,根据行程问题的数量关系:速度=路程时间,路程速度时间就可以求解;
()由()的结论可以求出点的坐标,再由题意可得点的坐标,由待定系数法求出的解析式;
()分当两车第一次相遇前相距千米的路程;当两车第一次相遇后,甲车到达地前,相距千米的路程;当甲车到达地后返回地,两车第二次相遇后,甲车到地距离共有千米,所以两车不可能再相距千米;分别求解即可.
【详解】(1)由函数图象可得:,两地相距路程是千米,
乙车行驶的速度是(千米/时),
图中括号内的数为:,
故答案为:,;
(2),甲车的速度为千米/时,
甲车从地到地需(小时),故点坐标,
设甲车从地返回地过程中与的函数解析式为,
将,代入上式,得
,
解得,
∴与的函数解析式为;
(3)设两车出发后小时相距千米的路程,
当两车第一次相遇前相距千米的路程,根据题意,得
,
解得:,
当两车第一次相遇后,甲车到达地前,相距千米的路程,根据题意,得
,
解得:,
当甲车到达地后返回甲地,两车第二次相遇时相距千米的路程,
∵,
∴乙在停留时两车第二次相遇时相距120千米,
根据题意,得,
解得:,
当甲车到达地后返回地,两车第二次相遇后,甲车到地距离共有千米,所以两车不可能再相距千米;
综上,两车出发后小时或小时或小时相距千米的路程.
故答案为:2或或.
【点睛】此题考查了待定系数法求一次函数的解析式,函数图象,一次函数与一元一次方程的运用,解答时从函数图象获取信息是解题的关键.
23.(1)①2;②2;(2);(3).
【分析】(1)①如图, 证明,可得,结合,,,从而可得答案;②如图,过作交于, 而,可得,再利用①的结论即可;
(2)如图,过作交于, 而,可得,同理可得:,过作交于,同理可得:四边形为平行四边形,可得,,结合①可得答案;
(3)如图,过作的平行线交的延长线于,过作的垂线交于,而,证明四边形为矩形,,设,则,求解,再结合(1)的结论可得答案.
【详解】解:(1)①如图,
∵矩形,
∴,
∴,
∵,
∴,
∴,
∴,
∴
∵,,,
∴,
∴;
②如图,过作交于, 而
∴,
∵矩形,
∴,
∴四边形是平行四边形,
∴,
由①可得:,
∴;
(2)如图,过作交于, 而
∴,
同理可得:,
过作交于,
同理可得:四边形为平行四边形,
∴,,
由①可得:,
∴;
(3)如图,过作的平行线交的延长线于,过作的垂线交于,而,
∴,,,
∴四边形为矩形,
∴,
∵,
∴,
设,则,
∵,
∴,
∵,
结合(1)的结论可得:.
【点睛】本题考查的是矩形的判定与性质,平行四边形的判定与性质,相似三角形的判定与性质,锐角三角函数的应用,熟练的利用类比的数学方法解题是关键.
24.(1),
(2)
(3)①存在,;②
【分析】(1)先求出,再运用待定系数法求出抛物线的函数关系式,即,再令,解出,即可作答.
(2)先表达,结合“恰好是以为底边的等腰三角形”得出,代入数值,运用因式分解法解方程,即可作答.
(3)①证明,根据,得出不变,则,即可作答.②在以为圆心,4为半径的半圆上,,结合运动轨迹,得出的最小值,再运用勾股定理列式计算,即可作答.
【详解】(1)解:在中,
令,则,
令,则,
,
把代入
得,
,
抛物线的函数关系式为:,
令,则,
,
;
(2)解:点,过点作轴的垂线分别与直线和抛物线交于、两点,
,
当为底时,作于,
则,
,
,
解得:(不合题意,舍去),
当时,恰好是以为底边的等腰三角形;
(3)解:①存在,,过程如下:
,
,
当时,,
不变,
即,
②将绕原点顺时针旋转得到(旋转角在到之间);
∴在以为圆心,4为半径的半圆上,
由①知,,
,
的最小值,
此时三点共线,
∵
的最小值.
【点睛】本题考查了二次函数的几何综合,解一元二次方程,相似三角形的判定与性质,勾股定理,正确掌握相关性质内容是解题的关键.
答案第1页,共2页
答案第1页,共2页
同课章节目录
