【沪科版八上同步练习】第13章 三角形中的边角关系命题和证明(基础知识)检测题(含答案)
文档属性
| 名称 | 【沪科版八上同步练习】第13章 三角形中的边角关系命题和证明(基础知识)检测题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-19 15:09:37 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【沪科版八上同步练习】
第13章三角形中的边角关系命题和证明(基础知识)检测题
一、单选题
1.对于命题“如果,那么”,下面四组关于a,b的值中,能说明这个命题是假命题的是( )
A., B., C., D.,
2.现有两根小木棒,它们的长度分别为 和 ,若要钉成一个三角形架,下列长度不可以作为第三根木棒长度的是( )
A. B. C. D.
3.设三角形三边之长分别为3,8,,则的值可能为( )
A.11 B.9 C.5 D.3
4.如图,在中,,、三等分,D、E在边上,则其中的相似三角形有( )
A.1对 B.2对 C.3对 D.6对
5.如图是两个全等的三角形纸片,其三边长之比为,按图中方法分别将其对折,使折痕(图中虚线)过其中的一个顶点,且使该顶点所在两边重合,记折叠后不重叠部分面积分别为,已知,则纸片的面积是( )
A.102 B.104 C.106 D.108
二、判断题
6.长度分别是6厘米、8厘米、10厘米的三根小棒,可以围成一个三角形。( )
7.一个三角形的三个内角之比是3∶1∶4,这是一个直角三角形.
三、填空题
8.命题:“如果|a|=|b|,那么a=b”的逆命题是: (填“真命题”或“假命题”).
9.在△ABC中,AB=AC, ,则∠C= °.
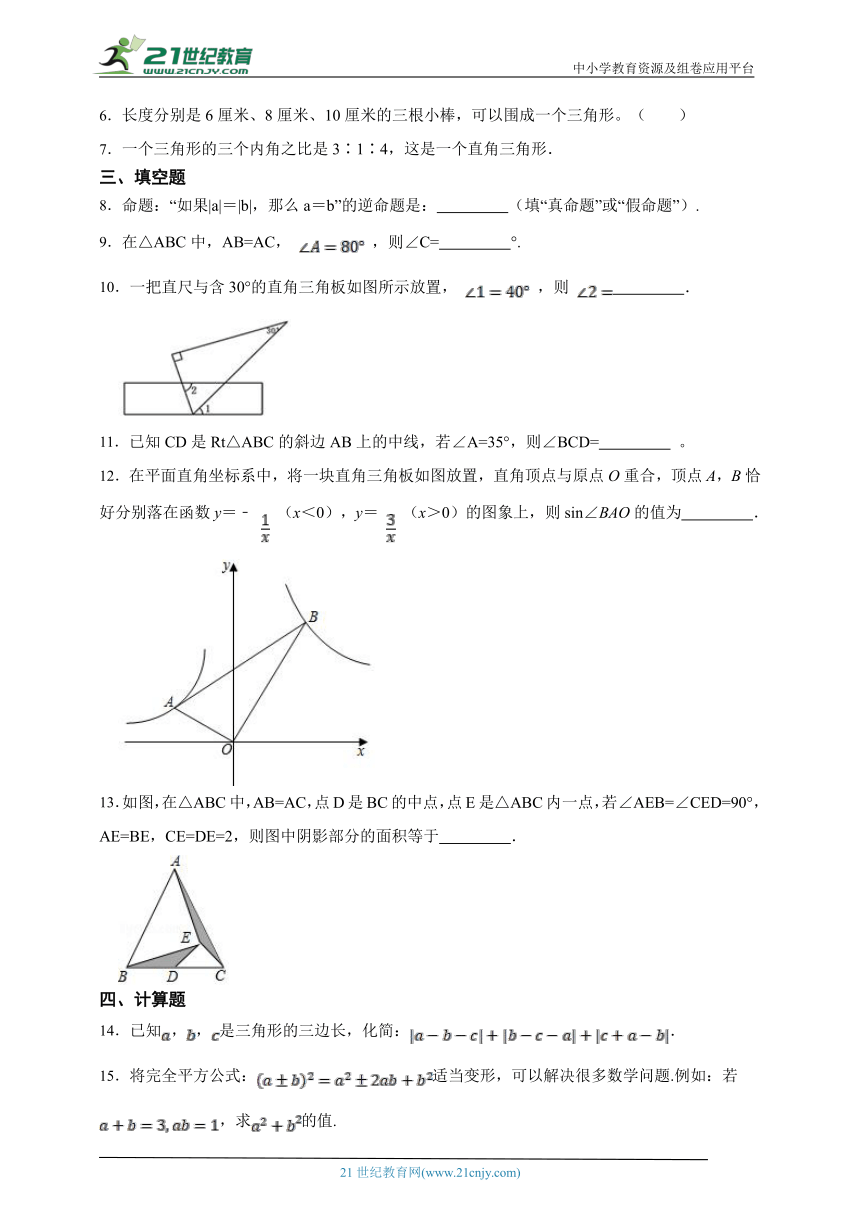
10.一把直尺与含30°的直角三角板如图所示放置, ,则 .
11.已知CD是Rt△ABC的斜边AB上的中线,若∠A=35°,则∠BCD= 。
12.在平面直角坐标系中,将一块直角三角板如图放置,直角顶点与原点O重合,顶点A,B恰好分别落在函数y=﹣ (x<0),y= (x>0)的图象上,则sin∠BAO的值为 .
13.如图,在△ABC中,AB=AC,点D是BC的中点,点E是△ABC内一点,若∠AEB=∠CED=90°,AE=BE,CE=DE=2,则图中阴影部分的面积等于 .
四、计算题
14.已知,,是三角形的三边长,化简:.
15.将完全平方公式:适当变形,可以解决很多数学问题.例如:若,求的值.
解:
又
根据上面的解题思路与方法,解决下列问题:
(1)若x-y=5,xy=2,求的值;
(2)若,求xy的值;
(3)如图,点C是线段AB上的一点,以AC,BC为边向两边作正方形,两正方形的面积分别为.若,求图中阴影部分的面积.【提示:可设】
16.在平面直角坐标系xOy中描出下列两组点,分别将每组里的点用线段依次连接起来.
第一组:A(﹣3,3)、C(4,3);
第二组:D(﹣2,﹣1)、E(2,﹣1).
(1)直接写出线段AC与线段DE的位置关系;
(2)在(1)的条件下,线段AC,DE分别与y轴交于点B,F.若点M为射线OB上一动点(不与点O,B重合).
①当点M在线段OB上运动时,连接AM、DM,补全图形,用等式表示∠CAM、∠AMD、∠MDE之间的数量关系,并证明.
②当△ACM与△DEM面积相等时,求点M的坐标.
五、解答题
17. 如图,Rt△ABC中,∠C = 90°,把Rt△ABC绕着B点逆时针旋转,得到Rt△DBE,点E在AB上.
(1)若∠BDA = 70°,求∠BAC的度数.
(2)若BC = 8,AC = 6,求△ABD中AD边上的高.
18.如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=40°,∠C=70°,
求:∠AEC和∠DAE的度数.
19.如果一个三角形中最大角是最小角的4倍,求它的最小角的取值范围.
六、综合题
20.如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
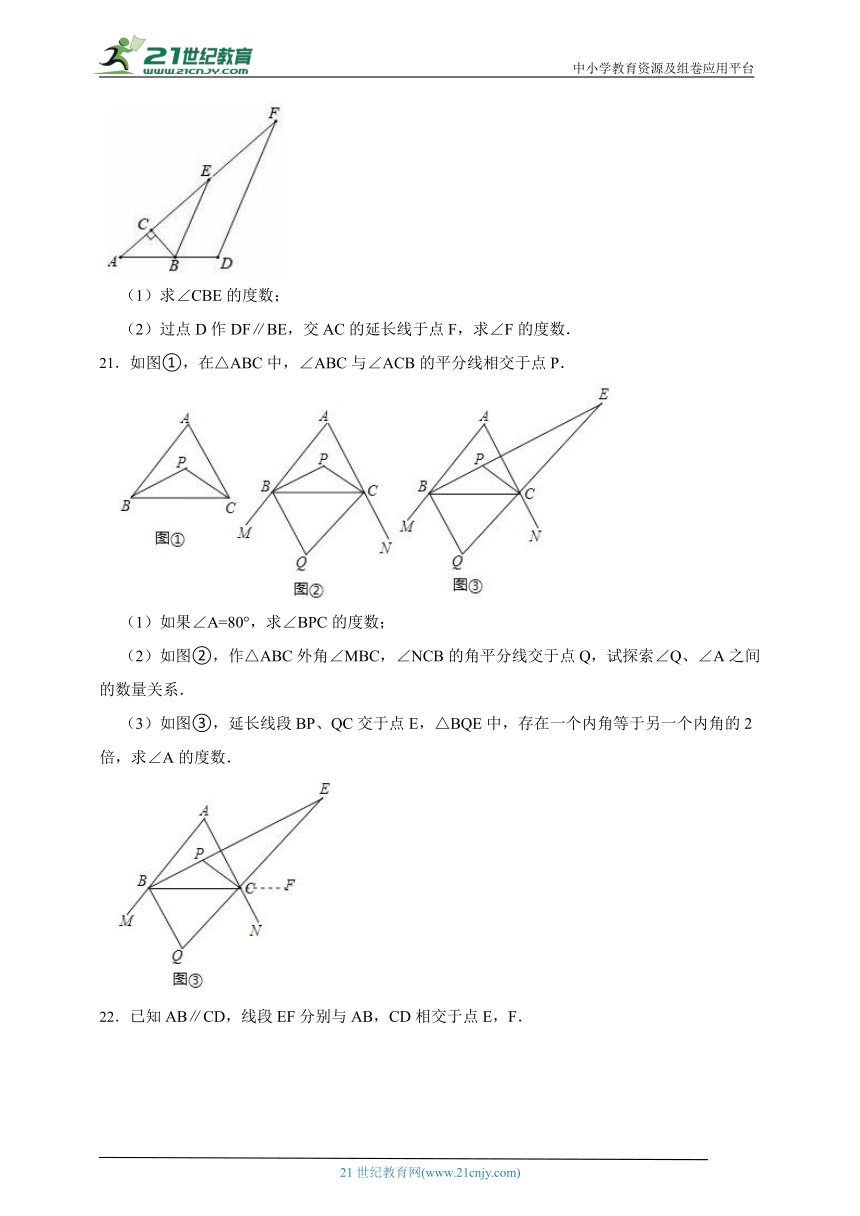
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
21.如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.
22.已知AB∥CD,线段EF分别与AB,CD相交于点E,F.
(1)请在横线上填上合适的内容,完成下面的解答:
如图1,当点P在线段EF上时,已知∠A=35°,∠C=62°,求∠APC的度数;
解:过点P作直线PH∥AB,
所以∠A=∠APH,依据是 ▲ ;
因为AB∥CD,PH∥AB,
所以PH∥CD,依据是 ▲ ;
所以∠C=( ),
所以∠APC=( ▲ )+( ▲ )=∠A+∠C=97°.
(2)当点P,Q在线段EF上移动时(不包括E,F两点):
①如图2,∠APQ+∠PQC=∠A+∠C+180°成立吗?请说明理由;
②如图3,∠APM=2∠MPQ,∠CQM=2∠MQP,∠M+∠MPQ+∠PQM=180°,请直接写出∠M,∠A与∠C的数量关系.
七、实践探究题
23.将三角形纸片 沿 折叠,使点 落在点 处.
(1)(感知)如图①,若点 落在四边形 的边 上,则 与 之间的数量关系是 .
(2)(探究)如图②,若点 落在四边形 的内部,则 与 之间存在怎样的数量关系?请说明理由.
(3)(拓展)如图③,若点 落在四边形 的外部, , ,则 的大小为 度.
答案解析部分
1.【答案】D
【知识点】真命题与假命题
2.【答案】D
【知识点】三角形三边关系
3.【答案】B
【知识点】三角形三边关系
4.【答案】D
【知识点】三角形内角和定理;等腰三角形的性质;相似三角形的判定
5.【答案】D
【知识点】三角形的面积;勾股定理;翻折变换(折叠问题)
6.【答案】正确
【知识点】三角形三边关系
7.【答案】正确
【知识点】三角形内角和定理
8.【答案】真命题
【知识点】真命题与假命题;逆命题
9.【答案】50
【知识点】三角形内角和定理;等腰三角形的性质
10.【答案】80°
【知识点】平行线的性质;三角形内角和定理
11.【答案】55°
【知识点】三角形的角平分线、中线和高;等腰三角形的性质
12.【答案】
【知识点】反比例函数系数k的几何意义;三角形的面积;勾股定理;相似三角形的判定与性质
13.【答案】4
【知识点】三角形的面积;三角形全等的判定
14.【答案】
【知识点】整式的加减运算;三角形三边关系;化简含绝对值有理数
15.【答案】(1)解:∵x-y=5,
∴(x-y)2=25,
又,
,
.
(2)解:,
又,
,
.
(3)解:设,则
又
【知识点】完全平方公式及运用;三角形的面积
16.【答案】(1)解:∵A(﹣3,3)、C(4,3),
∴AC∥x轴,
∵D(﹣2,﹣1)、E(2,﹣1),
∴DE∥x轴,
∴AC∥DE;
(2)①如图,∠CAM+∠MDE=∠AMD.
理由如下:
过点M作MN∥AC,
∵MN∥AC(作图),
∴∠CAM=∠AMN(两直线平行,内错角相等),
∵AC∥DE(已知),
∴MN∥DE(平行公理推论),
∴∠MDE=∠NMD(两直线平行,内错角相等),
∴∠CAM+∠MDE=∠AMN+∠NMD=∠AMD(等量代换).
②由题意,得:AC=7,DE=4,
设M(0,m),
(i)当点M在线段OB上时,BM=3﹣m,FM=m+1,
∴S△ACM= AC BM= ×7×(3﹣m)= ,
S△DEM= DE FM= ×4×(m+1)=2m+2,
∵S△ACM=S△DEM,
∴ =2m+2,
解得:m= ,
∴M(0, );
(ii)当点M在线段OB的延长线上时,BM=m﹣3,FM=m+1,
∴S△ACM= AC BM= ×7×(m﹣3)= ,
S△DEM= DE FM= ×4×(m+1)=2m+2,
∵S△ACM=S△DEM,
∴ =2m+2,
解得:m= ,
∴M(0, );
综上所述,点M的坐标为(0, )或(0, ).
【知识点】角的运算;平行线的判定与性质;三角形的面积
17.【答案】解:(1) 由旋转得△ACB≌△DEB
∴BD = BA
∴∠BAD =∠BDA =70°
∴∠ABD =40°
∴∠ABC =∠ABD =40°
∵∠C =90°
∴∠BAC =50°
(2) ∵BC = 8,AC = 6,∠C =90°
∴
∵∠DEB =∠C =且BE = BC = 8,DE ="AC" = 6
∴AE =" AB" – BE = 2
在Rt△DEA中,
设AD边上的高为h
∴
∴
【知识点】三角形的面积;三角形内角和定理;勾股定理;旋转的性质
18.【答案】解:∵∠B=40°,∠C=70°,
∴∠BAC=180°-∠B-∠C=70°,
∵AE是角平分线,
∴∠EAC= ∠BAC=35°.
∵AD是高,∠C=70°,
∴∠DAC=90°-∠C=20°,
∴∠DAE=∠EAC-∠DAC=35°-20°=15°,
∠AEC=90°-15°=75°.
【知识点】三角形内角和定理
19.【答案】解:设∠A是它的最小角,∠C是最大角,∠B是中间的角,则∠A≤∠B≤∠C,又∠C=4∠A.由可得∠A+∠A+4∠A≤180°,即么A≤30°.可得∠A+4∠A+4∠A≥180°,即∠A≥20°.所以最小角的取值范围为20°≤4≤30°.
【知识点】三角形内角和定理
20.【答案】(1)解:∵在Rt△ABC中,∠ACB=90°,∠A=40°,∴∠ABC=90°﹣∠A=50°,
∴∠CBD=130°.
∵BE是∠CBD的平分线,
∴∠CBE= ∠CBD=65°
(2)解:∵∠ACB=90°,∠CBE=65°,∴∠CEB=90°﹣65°=25°.∵DF∥BE,
∴∠F=∠CEB=25°
【知识点】平行线的性质;三角形内角和定理
21.【答案】(1)解:∵∠A=80°.
∴∠ABC+∠ACB=100°,
∵点P是∠ABC和∠ACB的平分线的交点,
∴∠P=180°﹣ (∠ABC+∠ACB)=180°﹣ ×100°=130°,
(2)解:∵外角∠MBC,∠NCB的角平分线交于点Q,
∴∠QBC+∠QCB= (∠MBC+∠NCB)
= (360°﹣∠ABC﹣∠ACB)
= (180°+∠A)
=90°+ ∠A
∴∠Q=90°﹣ ∠A;
(3)解:∵CQ为△ABC的外角∠NCB的角平分线,
∴CE是△ABC的外角∠ACF的平分线,
∴∠ACF=2∠ECF,
∵BE平分∠ABC,
∴∠ABC=2∠EBC,
∵∠ECF=∠EBC+∠E,
∴2∠ECF=2∠EBC+2∠E,
即∠ACF=∠ABC+2∠E,
又∵∠ACF=∠ABC+∠A,
∴∠A=2∠E,即∠E= ∠A;
∵∠EBQ=∠EBC+∠CBQ
= ∠ABC+ ∠MBC
= (∠ABC+∠A+∠ACB)=90°.
如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况:
①∠EBQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;
②∠EBQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;
③∠Q=2∠E,则90°﹣ ∠A=∠A,解得∠A=60°;
④∠E=2∠Q,则 ∠A=2(90°﹣ ∠A),解得∠A=120°.
综上所述,∠A的度数是90°或60°或120°.
【知识点】三角形内角和定理;三角形的外角性质
22.【答案】(1)解:过点P作直线PH∥AB,
所以∠A=∠APH,依据是两直线平行,内错角相等;
因为AB∥CD,PH∥AB,
所以PH∥CD,依据是平行于同一条直线的两条直线平行;
所以∠C=(∠CPH),
所以∠APC=(∠APH)+(∠CPH)=∠A+∠C=97°.
(2)解:①如图2,∠APQ+∠PQC=∠A+∠C+180°成立,理由如下:
过点P作直线PH∥AB,QG∥AB,
∵AB∥CD,
∴AB∥CD∥PH∥QG,
∴∠A=∠APH,∠C=∠CQG,∠HPQ+∠GQP=180°,
∴∠APQ+∠PQC=∠APH+∠HPQ+∠GQP+∠CQG=∠A+∠C+180°.
∴∠APQ+∠PQC=∠A+∠C+180°成立;
②如图3,
过点P作直线PH∥AB,QG∥AB,MN∥AB,
∵AB∥CD,
∴AB∥CD∥PH∥QG∥MN,
∴∠A=∠APH,∠C=∠CQG,∠HPQ+∠GQP=180°,∠HPM=∠PMN,∠GQM=∠QMN,
∴∠PMQ=∠HPM+∠GQM,
∵∠APM=2∠MPQ,∠CQM=2∠MQP,∠PMQ+∠MPQ+∠PQM=180°,
∴∠APM+∠CQM=∠A+∠C+∠PMQ=2∠MPQ+2∠MQP=2(180°﹣∠PMQ),
∴3∠PMQ+∠A+∠C=360°.
【知识点】角的运算;平行线的判定与性质;推理与论证
23.【答案】(1)2∠A=∠1
(2)解: .
理由:连结 .
∵ ,
∴
∴ .
由翻折,得
∴
∴2∠A=∠1+∠2
(3)28
【知识点】角的运算;三角形的外角性质;翻折变换(折叠问题)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【沪科版八上同步练习】
第13章三角形中的边角关系命题和证明(基础知识)检测题
一、单选题
1.对于命题“如果,那么”,下面四组关于a,b的值中,能说明这个命题是假命题的是( )
A., B., C., D.,
2.现有两根小木棒,它们的长度分别为 和 ,若要钉成一个三角形架,下列长度不可以作为第三根木棒长度的是( )
A. B. C. D.
3.设三角形三边之长分别为3,8,,则的值可能为( )
A.11 B.9 C.5 D.3
4.如图,在中,,、三等分,D、E在边上,则其中的相似三角形有( )
A.1对 B.2对 C.3对 D.6对
5.如图是两个全等的三角形纸片,其三边长之比为,按图中方法分别将其对折,使折痕(图中虚线)过其中的一个顶点,且使该顶点所在两边重合,记折叠后不重叠部分面积分别为,已知,则纸片的面积是( )
A.102 B.104 C.106 D.108
二、判断题
6.长度分别是6厘米、8厘米、10厘米的三根小棒,可以围成一个三角形。( )
7.一个三角形的三个内角之比是3∶1∶4,这是一个直角三角形.
三、填空题
8.命题:“如果|a|=|b|,那么a=b”的逆命题是: (填“真命题”或“假命题”).
9.在△ABC中,AB=AC, ,则∠C= °.
10.一把直尺与含30°的直角三角板如图所示放置, ,则 .
11.已知CD是Rt△ABC的斜边AB上的中线,若∠A=35°,则∠BCD= 。
12.在平面直角坐标系中,将一块直角三角板如图放置,直角顶点与原点O重合,顶点A,B恰好分别落在函数y=﹣ (x<0),y= (x>0)的图象上,则sin∠BAO的值为 .
13.如图,在△ABC中,AB=AC,点D是BC的中点,点E是△ABC内一点,若∠AEB=∠CED=90°,AE=BE,CE=DE=2,则图中阴影部分的面积等于 .
四、计算题
14.已知,,是三角形的三边长,化简:.
15.将完全平方公式:适当变形,可以解决很多数学问题.例如:若,求的值.
解:
又
根据上面的解题思路与方法,解决下列问题:
(1)若x-y=5,xy=2,求的值;
(2)若,求xy的值;
(3)如图,点C是线段AB上的一点,以AC,BC为边向两边作正方形,两正方形的面积分别为.若,求图中阴影部分的面积.【提示:可设】
16.在平面直角坐标系xOy中描出下列两组点,分别将每组里的点用线段依次连接起来.
第一组:A(﹣3,3)、C(4,3);
第二组:D(﹣2,﹣1)、E(2,﹣1).
(1)直接写出线段AC与线段DE的位置关系;
(2)在(1)的条件下,线段AC,DE分别与y轴交于点B,F.若点M为射线OB上一动点(不与点O,B重合).
①当点M在线段OB上运动时,连接AM、DM,补全图形,用等式表示∠CAM、∠AMD、∠MDE之间的数量关系,并证明.
②当△ACM与△DEM面积相等时,求点M的坐标.
五、解答题
17. 如图,Rt△ABC中,∠C = 90°,把Rt△ABC绕着B点逆时针旋转,得到Rt△DBE,点E在AB上.
(1)若∠BDA = 70°,求∠BAC的度数.
(2)若BC = 8,AC = 6,求△ABD中AD边上的高.
18.如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=40°,∠C=70°,
求:∠AEC和∠DAE的度数.
19.如果一个三角形中最大角是最小角的4倍,求它的最小角的取值范围.
六、综合题
20.如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
21.如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.
22.已知AB∥CD,线段EF分别与AB,CD相交于点E,F.
(1)请在横线上填上合适的内容,完成下面的解答:
如图1,当点P在线段EF上时,已知∠A=35°,∠C=62°,求∠APC的度数;
解:过点P作直线PH∥AB,
所以∠A=∠APH,依据是 ▲ ;
因为AB∥CD,PH∥AB,
所以PH∥CD,依据是 ▲ ;
所以∠C=( ),
所以∠APC=( ▲ )+( ▲ )=∠A+∠C=97°.
(2)当点P,Q在线段EF上移动时(不包括E,F两点):
①如图2,∠APQ+∠PQC=∠A+∠C+180°成立吗?请说明理由;
②如图3,∠APM=2∠MPQ,∠CQM=2∠MQP,∠M+∠MPQ+∠PQM=180°,请直接写出∠M,∠A与∠C的数量关系.
七、实践探究题
23.将三角形纸片 沿 折叠,使点 落在点 处.
(1)(感知)如图①,若点 落在四边形 的边 上,则 与 之间的数量关系是 .
(2)(探究)如图②,若点 落在四边形 的内部,则 与 之间存在怎样的数量关系?请说明理由.
(3)(拓展)如图③,若点 落在四边形 的外部, , ,则 的大小为 度.
答案解析部分
1.【答案】D
【知识点】真命题与假命题
2.【答案】D
【知识点】三角形三边关系
3.【答案】B
【知识点】三角形三边关系
4.【答案】D
【知识点】三角形内角和定理;等腰三角形的性质;相似三角形的判定
5.【答案】D
【知识点】三角形的面积;勾股定理;翻折变换(折叠问题)
6.【答案】正确
【知识点】三角形三边关系
7.【答案】正确
【知识点】三角形内角和定理
8.【答案】真命题
【知识点】真命题与假命题;逆命题
9.【答案】50
【知识点】三角形内角和定理;等腰三角形的性质
10.【答案】80°
【知识点】平行线的性质;三角形内角和定理
11.【答案】55°
【知识点】三角形的角平分线、中线和高;等腰三角形的性质
12.【答案】
【知识点】反比例函数系数k的几何意义;三角形的面积;勾股定理;相似三角形的判定与性质
13.【答案】4
【知识点】三角形的面积;三角形全等的判定
14.【答案】
【知识点】整式的加减运算;三角形三边关系;化简含绝对值有理数
15.【答案】(1)解:∵x-y=5,
∴(x-y)2=25,
又,
,
.
(2)解:,
又,
,
.
(3)解:设,则
又
【知识点】完全平方公式及运用;三角形的面积
16.【答案】(1)解:∵A(﹣3,3)、C(4,3),
∴AC∥x轴,
∵D(﹣2,﹣1)、E(2,﹣1),
∴DE∥x轴,
∴AC∥DE;
(2)①如图,∠CAM+∠MDE=∠AMD.
理由如下:
过点M作MN∥AC,
∵MN∥AC(作图),
∴∠CAM=∠AMN(两直线平行,内错角相等),
∵AC∥DE(已知),
∴MN∥DE(平行公理推论),
∴∠MDE=∠NMD(两直线平行,内错角相等),
∴∠CAM+∠MDE=∠AMN+∠NMD=∠AMD(等量代换).
②由题意,得:AC=7,DE=4,
设M(0,m),
(i)当点M在线段OB上时,BM=3﹣m,FM=m+1,
∴S△ACM= AC BM= ×7×(3﹣m)= ,
S△DEM= DE FM= ×4×(m+1)=2m+2,
∵S△ACM=S△DEM,
∴ =2m+2,
解得:m= ,
∴M(0, );
(ii)当点M在线段OB的延长线上时,BM=m﹣3,FM=m+1,
∴S△ACM= AC BM= ×7×(m﹣3)= ,
S△DEM= DE FM= ×4×(m+1)=2m+2,
∵S△ACM=S△DEM,
∴ =2m+2,
解得:m= ,
∴M(0, );
综上所述,点M的坐标为(0, )或(0, ).
【知识点】角的运算;平行线的判定与性质;三角形的面积
17.【答案】解:(1) 由旋转得△ACB≌△DEB
∴BD = BA
∴∠BAD =∠BDA =70°
∴∠ABD =40°
∴∠ABC =∠ABD =40°
∵∠C =90°
∴∠BAC =50°
(2) ∵BC = 8,AC = 6,∠C =90°
∴
∵∠DEB =∠C =且BE = BC = 8,DE ="AC" = 6
∴AE =" AB" – BE = 2
在Rt△DEA中,
设AD边上的高为h
∴
∴
【知识点】三角形的面积;三角形内角和定理;勾股定理;旋转的性质
18.【答案】解:∵∠B=40°,∠C=70°,
∴∠BAC=180°-∠B-∠C=70°,
∵AE是角平分线,
∴∠EAC= ∠BAC=35°.
∵AD是高,∠C=70°,
∴∠DAC=90°-∠C=20°,
∴∠DAE=∠EAC-∠DAC=35°-20°=15°,
∠AEC=90°-15°=75°.
【知识点】三角形内角和定理
19.【答案】解:设∠A是它的最小角,∠C是最大角,∠B是中间的角,则∠A≤∠B≤∠C,又∠C=4∠A.由可得∠A+∠A+4∠A≤180°,即么A≤30°.可得∠A+4∠A+4∠A≥180°,即∠A≥20°.所以最小角的取值范围为20°≤4≤30°.
【知识点】三角形内角和定理
20.【答案】(1)解:∵在Rt△ABC中,∠ACB=90°,∠A=40°,∴∠ABC=90°﹣∠A=50°,
∴∠CBD=130°.
∵BE是∠CBD的平分线,
∴∠CBE= ∠CBD=65°
(2)解:∵∠ACB=90°,∠CBE=65°,∴∠CEB=90°﹣65°=25°.∵DF∥BE,
∴∠F=∠CEB=25°
【知识点】平行线的性质;三角形内角和定理
21.【答案】(1)解:∵∠A=80°.
∴∠ABC+∠ACB=100°,
∵点P是∠ABC和∠ACB的平分线的交点,
∴∠P=180°﹣ (∠ABC+∠ACB)=180°﹣ ×100°=130°,
(2)解:∵外角∠MBC,∠NCB的角平分线交于点Q,
∴∠QBC+∠QCB= (∠MBC+∠NCB)
= (360°﹣∠ABC﹣∠ACB)
= (180°+∠A)
=90°+ ∠A
∴∠Q=90°﹣ ∠A;
(3)解:∵CQ为△ABC的外角∠NCB的角平分线,
∴CE是△ABC的外角∠ACF的平分线,
∴∠ACF=2∠ECF,
∵BE平分∠ABC,
∴∠ABC=2∠EBC,
∵∠ECF=∠EBC+∠E,
∴2∠ECF=2∠EBC+2∠E,
即∠ACF=∠ABC+2∠E,
又∵∠ACF=∠ABC+∠A,
∴∠A=2∠E,即∠E= ∠A;
∵∠EBQ=∠EBC+∠CBQ
= ∠ABC+ ∠MBC
= (∠ABC+∠A+∠ACB)=90°.
如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况:
①∠EBQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;
②∠EBQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;
③∠Q=2∠E,则90°﹣ ∠A=∠A,解得∠A=60°;
④∠E=2∠Q,则 ∠A=2(90°﹣ ∠A),解得∠A=120°.
综上所述,∠A的度数是90°或60°或120°.
【知识点】三角形内角和定理;三角形的外角性质
22.【答案】(1)解:过点P作直线PH∥AB,
所以∠A=∠APH,依据是两直线平行,内错角相等;
因为AB∥CD,PH∥AB,
所以PH∥CD,依据是平行于同一条直线的两条直线平行;
所以∠C=(∠CPH),
所以∠APC=(∠APH)+(∠CPH)=∠A+∠C=97°.
(2)解:①如图2,∠APQ+∠PQC=∠A+∠C+180°成立,理由如下:
过点P作直线PH∥AB,QG∥AB,
∵AB∥CD,
∴AB∥CD∥PH∥QG,
∴∠A=∠APH,∠C=∠CQG,∠HPQ+∠GQP=180°,
∴∠APQ+∠PQC=∠APH+∠HPQ+∠GQP+∠CQG=∠A+∠C+180°.
∴∠APQ+∠PQC=∠A+∠C+180°成立;
②如图3,
过点P作直线PH∥AB,QG∥AB,MN∥AB,
∵AB∥CD,
∴AB∥CD∥PH∥QG∥MN,
∴∠A=∠APH,∠C=∠CQG,∠HPQ+∠GQP=180°,∠HPM=∠PMN,∠GQM=∠QMN,
∴∠PMQ=∠HPM+∠GQM,
∵∠APM=2∠MPQ,∠CQM=2∠MQP,∠PMQ+∠MPQ+∠PQM=180°,
∴∠APM+∠CQM=∠A+∠C+∠PMQ=2∠MPQ+2∠MQP=2(180°﹣∠PMQ),
∴3∠PMQ+∠A+∠C=360°.
【知识点】角的运算;平行线的判定与性质;推理与论证
23.【答案】(1)2∠A=∠1
(2)解: .
理由:连结 .
∵ ,
∴
∴ .
由翻折,得
∴
∴2∠A=∠1+∠2
(3)28
【知识点】角的运算;三角形的外角性质;翻折变换(折叠问题)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
