小升初常考易错卷(试题)2023-2024学年数学六年级下册人教版(含解析)
文档属性
| 名称 | 小升初常考易错卷(试题)2023-2024学年数学六年级下册人教版(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 496.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-20 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
小升初常考易错卷(试题)2023-2024学年数学六年级下册人教版
一、选择题
1.下图中共有( )条线段。
A.8 B.10 C.5 D.4
2.一个三位数,既是2、3的倍数,也是5的倍数,这个数最小是( )。
A.120 B.102 C.105 D.150
3.如果甲×0.25=乙÷0.25(甲、乙都不为0),那么甲( )乙。
A.> B.= C.< D.无法确定
4.圆柱的底面半径和高都扩大到原来的2倍,它的体积扩大到原来的( )倍。
A.2 B.4 C.6 D.8
5.甲住一楼,乙住三楼,丙住五楼。昨天下午,甲先到乙家,等乙扫完地后他们去找丙;刚上五楼就遇到了丙,于是三人立即一起下楼去玩。下面( )比较准确地描述了甲的活动。
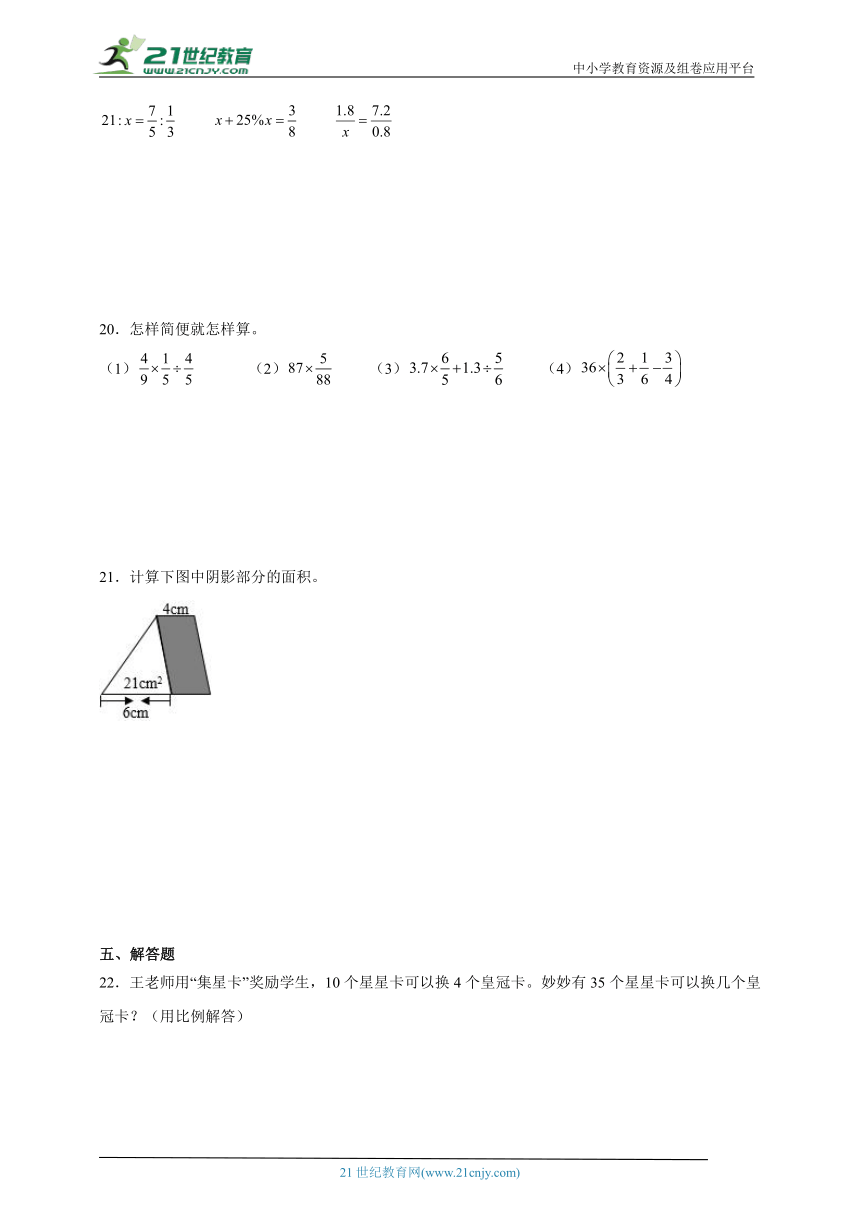
A. B.
C. D.
6.下列说法中,正确的有( )句。
①用四个圆心角为90°的扇形,一定可以拼成一个圆。
②修一条公路,如果由甲工程队单独修,65天可以完成;如果由乙工程队单独修,75天可以完成。现在由甲、乙两个工程队合修,40天一定能修完。
③在一块长2米、宽1.6米的长方形铁板上,最多能截取40个半径是2分米的圆形铁板。
④水果店的香蕉10月第一周比上一周涨价10%,第二周比第一周涨价10%,两周以来共涨价20%。
A.3 B.2 C.1 D.0
二、填空题
7.六(1)班有38人,他们中至少有( )人在同一个月过生日。
8.在括号里填上合适的数或单位。
2460米=( )千米;1时20分=( )分;2公顷=( )平方米。
9.一个长6cm,宽4cm的长方形按5∶1放大,得到的图形面积是( )cm2。
10.一块长方形的地,长60米,宽40米,用1∶100的比例尺把它画在图纸上,图纸上这个长方形的周长是( )厘米。
11.把一根总长6m的圆柱形木料截成3段小圆柱,表面积比原木料增加12.4m2,这根圆柱形木料的体积是( )m3。
12.如图,两个同心圆中间有一个正方形,正方形的面积是10平方厘米,外圆的面积是( )平方厘米,外圆的面积与内圆的面积比是( )∶( )。
三、判断题
13.如果一个长方体四个面完全一样,那么另外两个面是正方形。( )
14.圆柱的体积一定,圆柱的高与底面积成正比例关系。( )
15.一个三角形3个内角的度数比是1∶4∶5,那么这一定是个直角三角形。( )
16.a是一个整数,它的倒数一定是。( )
17.如果a×=b×80%(a,b均不为),那么a∶b=6∶5。( )
四、计算题
18.直接等结果。
3.5÷0.07= 10÷10%= 10-10%=
19.求未知数。
20.怎样简便就怎样算。
(1) (2) (3) (4)
21.计算下图中阴影部分的面积。
五、解答题
22.王老师用“集星卡”奖励学生,10个星星卡可以换4个皇冠卡。妙妙有35个星星卡可以换几个皇冠卡?(用比例解答)
23.小明养成了喜欢读书的好习惯。妈妈给他买回一本课外书,第一天看了,第二天看了95页,第三天又看了,正好看完。这本书共有多少页?
24.为了鼓励市民节约用水,某市采用了分段计费的方式,收费标准如下表:
每月用水量 收费标准
第一阶梯 0-17吨(含) 3.4元/吨
第二阶梯 超过17吨的部分 5.3元/吨
(1)小丽家本月用水15吨,需要交水费多少元?
(2)小涛家本月交水费79元,他家这个月用了多少吨水?
25.一定时间内,降落在水平地面上的水,在未经蒸发、渗漏、流失情况下所累积的高度称为降雨量(通常以毫米作单位)。测定降雨量常用的容器是量筒和雨量器。我国气象规定,按24小时降水量为标准,降水级别如下表。某地区的土地面积大约是1000平方千米,每年用于绿化用水4000万立方米。2021年7月23日该地区的日平均降雨量是220毫米,这一天整个地区的降水量能满足一年的绿化用水量吗?
级别 小雨 中雨 大雨 暴雨 大暴雨 特大暴雨
降水量/mm 10以下 10~24.9 25~49.9 50~99.9 100-199.9 200以上
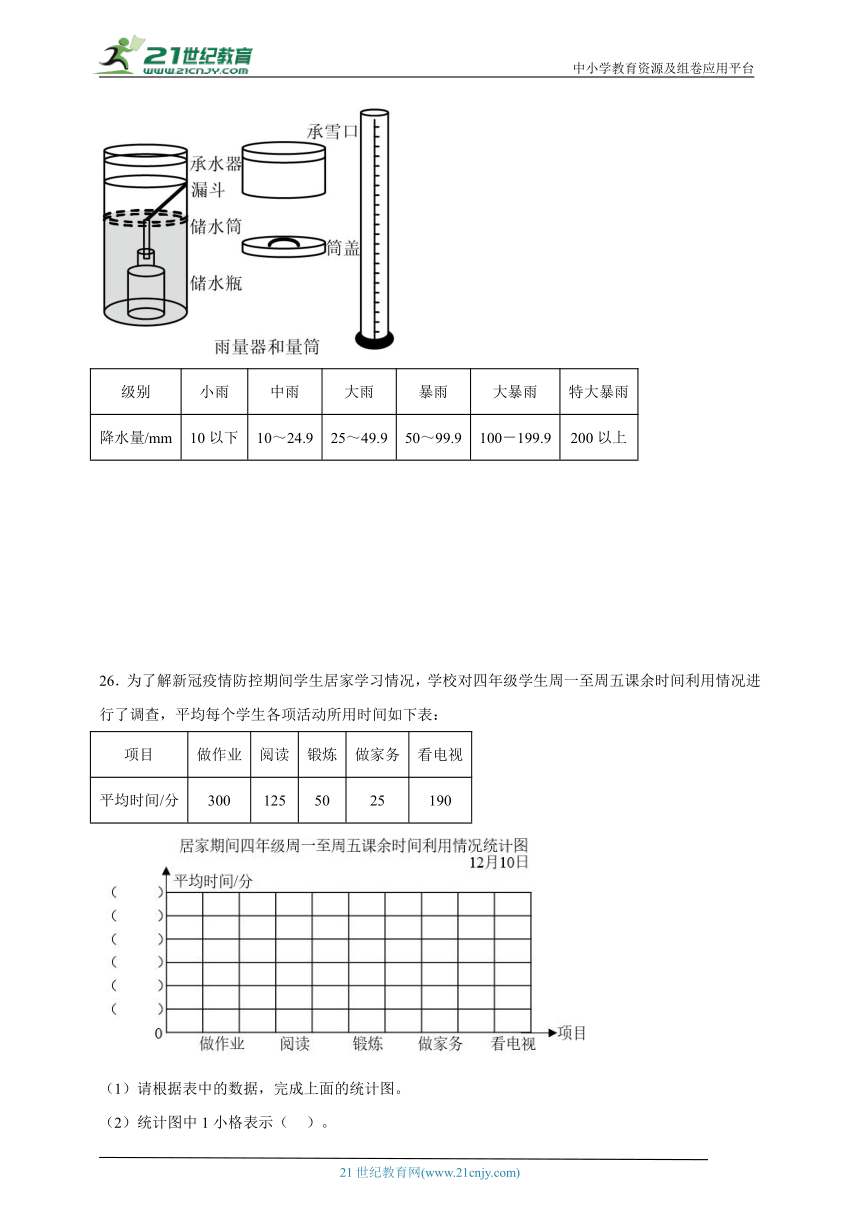
26.为了解新冠疫情防控期间学生居家学习情况,学校对四年级学生周一至周五课余时间利用情况进行了调查,平均每个学生各项活动所用时间如下表:
项目 做作业 阅读 锻炼 做家务 看电视
平均时间/分 300 125 50 25 190
(1)请根据表中的数据,完成上面的统计图。
(2)统计图中1小格表示( )。
(3)你有什么好的建议吗?(至少提两条)
参考答案:
1.B
【分析】含2个端点的线段有4条,含3个端点的线段有3条,含4个端点的线段有2条,含5个端点的线段有1条,依此计算出线段的总条数即可。
【详解】4+3+2+1=10(条),即图中共有10条线段。
故答案为:B
【点睛】熟练掌握线段的特点是解答此题的关键。
2.A
【分析】个位数字是0或者5的数,是5的倍数,根据2的特征,个位数字只能为0,这个三位数三个数位上的数字之和是3的倍数,那么这个数就是3的倍数,据此综合判断即可。
【详解】由分析可得:
该三位数既满足2、3、5倍数特征,又要求最小,所以百位上的数字是1,同时个位上的数字是0,此时百位和个位的数字之和为:
1+0=1
十位上的数字可以是2、5、8,满足三位数最小,所以十位上的数字是2,即该三位数为120,
各个数位的和为:
1+2+0
=3+0
=3
满足3的倍数,同时也满足2和5的倍数。
故答案为:A
【点睛】本题考查了2、3和5的倍数特征,该数是2、3和5的倍数,也就是既要符合2、3的倍数特征,也要符合5的倍数特征,缺一不可。
3.A
【分析】假设甲×0.25=乙÷0.25=1(甲数、乙数都不为0),则甲数=4、乙数=0.25,由此即可得出甲数、乙数的大小。
【详解】假设甲×0.25=乙÷0.25=1(甲数、乙数都不为0)
则甲数=4、乙数=0.25
因为4>0.25
则甲数>乙数
故答案为:A
【点睛】本题运用假设法,分别求出甲数、乙数的值,再比较大小,做出选择。
4.D
【分析】根据圆柱特征,圆柱底面是一个圆,圆的面积公式为:S=r2,圆柱体积公式:V=Sh,由此可得出圆柱体积公式可以表示为:V=r2h,圆柱的底面半径和高都扩大到原来的2倍,根据积的变化规律:两数相乘,其中一个因数乘m或者除以m(0除外),另一个因数乘n或者除以n(0除外),积就乘mn或者除以mn(0除外),据此判断即可。
【详解】由分析可得:
因为V=r2h,因数r扩大到原来的2倍,则r2扩大到原来的倍数为:2×2=4,另一个因数h扩大到原来的2倍,则体积扩大的倍数为:
4×2=8
即体积扩大到原来的8倍。
故答案为:D
【点睛】本题考查了圆柱体积公式的应用,以及积的变化规律的应用。
5.B
【分析】首先甲家在一楼,所以在0时,甲的楼层为0,甲先到乙家,等乙扫完地后,所以在上升一个高度后要有横着的一段时间,等乙扫完地后,他们去找丙,楼层高度再增加,刚上五楼就遇到丙,于是三人立即一起下楼去玩,那么没有停留,没有横着的时间,楼层高度在下降直至为0。据此解答。
【详解】根据分析可知,较准确地描述了甲的活动的折线统计图是:
故答案为:B
【点睛】解答此题的关键是根据题意分析折线统计图,进而得出答案。
6.C
【分析】①半径决定圆的大小,如果半径不一样,扇形无法拼成一个圆;
②把这项工程看作单位“1”,甲工程队单独修,65天可以完成,甲每天修,乙工程队单独修,75天可以完成,乙每天修,根据工作时间=工作总量÷工作效率和,1÷(+)即可求出两队合作需要的天数;
③先把长和宽的单位化为分米,然后用除法计算长有多少(2×2)分米,宽有多少个(2×2)分米,然后根据乘法计算出最多可以截取多少个半径是2分米的圆形铁板;
④把上一周香蕉的价格看作单位“1”,已知第一周比上一周涨价10%,则第一周的价格是上一周的(1+10%),再把第一周的价格看作单位“1”,又已知第二周比第一周涨价10%,则第二周的价格是第一周的(1+10%),根据百分数乘法的意义,用1×(1+10%)×(1+10%)即可求出第二周的价格,再根据求一个数比另一个数多百分之几,用相差数除以另一个数再×100%,则用第二周的价格减去上一周的价格,然后用它们的差除以上一周的价格再乘100%,据此求出两周涨价的幅度;
【详解】①半径不能确定是否一样,那就说明扇形的大小不一样,就不一定可以拼成一个圆,所以原题说法错误;
②1÷(+)
=1÷
≈34.8(天)
所以原题说法正确;
③2米=20分米
1.6米=16分米
2×2=4(分米)
直径是4分米,
长可以截取20÷4=5(个)
宽可以截取16÷4=4(个)
5×4=20(个)
所以原题说法错误。
④[1×(1+10%)×(1+10%)-1]÷1×100%
=[1×1.1×1.1-1] ÷1×100%
=[1.21-1] ÷1×100%
=0.21÷1×100%
=21%
原题说法错误。
由此可知正确的有1句。
故答案为:C
【点睛】本题考查了工程问题、百分数的应用以及剪拼问题等,结合题意分析解答即可。
7.4
【分析】在此类抽屉问题中,至少数=被分配的物体数除以抽屉数的商+1(有余的情况下)。在本题中,被分配的物体数是38,抽屉数是12(一年有12个月),据此计算即可。
【详解】38÷12=3(人)……2(人)
3+1=4(人)
六(1)班有38人,他们中至少有4人在同一个月过生日。
【点睛】抽屉原理问题的解答思路是:要从最不利情况考虑,准确地建立抽屉和确定元素的总个数,然后根据“至少数=元素的总个数÷抽屉的个数+1(有余数的情况下)”解答。
8. 2.46 80 20000
【分析】1千米=1000米,1时=60分,1公顷=10000平方米,据此进率,根据单位之间的换算,大单位换算成小单位要乘它们之间的进率;小单位换算成大单位要除以它们之间的进率。
【详解】2460米=2.46千米
1时20分=80分
2公顷=20000平方米
【点睛】本题考查了长度单位及面积单位的换算。
9.600
【分析】因为按5∶1放大,所以长方形的长是6×5=30(cm),宽是4×5=20(cm),根据长方形的面积=长×宽,求出扩大后的长方形的面积即可。
【详解】6×5=30(cm)
4×5=20(cm)
30×20=600(cm2)
得到的图形的面积是600cm2。
【点睛】此题考查的图形的放大与缩小,求出放大后的长方形的长和宽,是解答此题的关键。
10.200
【分析】根据比例尺先求图上长方形的长,再求图上长方形的宽,最后根据长方形周长的计算公式计算长方形的周长。
【详解】因为60米=6000厘米,40米=4000厘米
则6000×=60(厘米)
4000×=40(厘米)
(60+40)×2=100×2=200(厘米)
所以图纸上这个长方形的周长是200厘米。
【点睛】重点是将长方形的长和宽进行单位换算。
11.18.6
【分析】根据圆柱的切割特点可知,切成3段后,表面积比原来增加了4个圆柱的底面的面积,由此利用增加的表面积12.4m2除以4即可得出圆柱的一个底面的面积,再利用圆柱的体积公式:V=Sh,即可求出这根木料的体积。
【详解】12.4÷4×6
=3.1×6
=18.6(m3)
所以,这根圆柱形木料的体积是18.6m3。
【点睛】抓住圆柱的切割特点和增加的表面积,先求出圆柱的底面积是解决此类问题的关键。
12. 15.7 2 1
【分析】因为正方形面积是边长的平方,正方形的边长又是内圆的直径,正方形的对角线又是外圆的直径,由此可求出内外圆的面积。
【详解】解:设正方形的边长为a厘米,a×a=10平方厘米
S内圆=3.14
=7.85(平方厘米)
设外圆半径为r厘米。
2r×r÷2×2=10
2r×r=10
r×r=5
S外圆=3.14×r×r
=3.14×5
=15.7(平方厘米)
15.7∶7.85
=(15.7÷7.85)∶(7.85÷7.85)
=2∶1
【点睛】本学生题主要考查了学生的观察能力,以及对圆与正方形特征的掌握。
13.√
【分析】长方体中如有两个面是正方形,那么这两个面一定是相对的面,这两个相对的面上的8条棱长度一定相等,剩下的也就是4个长方形不在正方形面上的4条棱也相等,所以一个长方体中有四个面完全一样,那么另外两个面一定是正方形。
【详解】假如长方体中两个正方形面是左右面,那么这个长方体的宽和高的长度相等,进而可得出4个长方形面的宽都相等,又由于剩下的4条长相等,所以一个长方体中有四个面完全一样,那么另外两个面是正方形;
故答案为:√
【点睛】此题考查的长方体是一种特殊的长方体,需要记住:“有两个面是正方形的长方体,另外四个长方形的面一定完全相同”这个结论,现实生活中很多包装盒都是做成这种形状。
14.×
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例。
【详解】底面积×高=圆柱的体积(一定)
乘积一定,那么圆柱的高与底面积成反比例关系。
原题说法错误。
故答案为:×
【点睛】掌握正、反比例的意义及辨识方法是解题的关键。
15.√
【分析】三角形3个内角的度数比是1∶4∶5,进而可得最大角的度数占三角形内角和的,三角形的内角和是180°,接下来利用乘法的意义,按照求一个数的几分之几是多少的方法,即可求出这个三角形的最大角的度数,再去判断三角形的类型。
【详解】180°×
=180°×
=90°
最大角是90°,有一个角是直角的三角形是直角三角形。
故答案为:√
【点睛】此题重点考查对比的意义的理解和根据角对三角形分类的方法。
16.×
【分析】根据乘积是1的两个数互为倒数,举例说明即可。
【详解】0是整数,但是0没有倒数。
故答案为:×
【点睛】找非0自然数的倒数,可以用1除以这个数。
17.√
【分析】比例的基本性质:外项之积=内项之积,所以如果a×=b×80%,则a∶b=80%∶,再把百分数化成分数,最后进行化简分数比,化简时把比号改为除号,用求比值的方法进行化简即可。
【详解】因为a×=b×80%
所以a∶b=80%∶=∶==6∶5
故答案为:√
【点睛】掌握比例的基本性质和分数比的化简方法是关键。
18.50;;9.9;0.65;
0.2;;;0.01;
【详解】略
19.;;
【分析】根据比例的性质,将原式化成,然后根据等式的性质,方程两边同时除以;
将原式化简成,然后根据等式的性质,方程两边同时除以1.25;
根据比例的性质,将原式化成,然后根据等式的性质,方程两边同时除以7.2。
【详解】
解:
解:
解:
20.(1);(2);(3)6;(4)3
【分析】(1)先把分数除法化为分数乘法,再利用乘法结合律简便计算;
(2)先把87化为(88-1),再利用乘法分配律简便计算;
(3)先把分数除法化为分数乘法,再利用乘法分配律简便计算;
(4)利用乘法分配律简便计算。
【详解】(1)
=
=
=
=
(2)
=
=
=
=
(3)
=
=
=
=6
(4)
=
=
=3
21.28()
【分析】阴影部分是一个平行四边形,它的高和三角形的高相等,据公式:三角形的面积=底×高÷2,推出三角形的高=三角形的面积×2÷底,再利用公式:平行四边形的面积=底×高,据此求出阴影部分的面积即可。
【详解】21×2÷6×4
=42÷6×4
=7×4
=28()
【点睛】知道阴影部分的高和三角形的高相等,根据三角形面积公式计算出高,这是解决此题的关键。
22.14个
【分析】根据题意可知,星星卡的个数和皇冠卡的比值一定,因此星星卡的个数和皇冠卡成正比例,假设35个星星卡可以换x个皇冠卡,据此列方程为:35∶x=10∶4,然后解出方程即可。
【详解】解:设35个星星卡可以换x个皇冠卡。
35∶x=10∶4
10x=35×4
10x=140
x=140÷10
x=14
答:妙妙有35个星星卡可以换14个皇冠卡。
【点睛】本题考查了正比例的应用,找出题目中的等量关系,是解答此题的关键。
23.150页
【分析】根据题意可知,小明读完这本书的过程可分为3部分,①第一天看了;②第二天看了95页;③第三天又看了。其中两部分用分率表示,一部分用具体数量表示。则可知这部分具体数量占单位“1”减去其中两部分的分率,再用具体数量除以对应的分率,就得到这本书共有多少页;可列式为95÷(1--)。
【详解】95÷(1--)
=95÷(1--)
=95÷
=95×
=150(页)
答:这本书共有150页。
【点睛】本题是把整本书的页数看作单位“1”,明确单位“1”未知,用除法计算,且能够熟练计算出具体数量所对应的分率,是解题关键。
24.(1)51元;
(2)21吨
【分析】(1)当用水量为15吨时,按每吨3.4元收费,根据“总价=单价×数量”求出小丽家本月的水费;
(2)先根据“总价=单价×数量”表示用水量为17吨时需要交的水费,再表示超过17吨的部分交的水费,利用“数量=总价÷单价”计算超过17吨的用水量,最后加上17吨,据此解答。
【详解】(1)15×3.4=51(元)
答:需要交水费51元。
(2)(79-17×3.4)÷5.3+17
=(79-57.8)÷5.3+17
=21.2÷5.3+17
=4+17
=21(吨)
答:他家这个月用了21吨水。
【点睛】本题主要考查分段计费,明确不同用水量对应的收费标准是解答题目的关键。
25.能满足
【分析】根据1平方千米=1000000平方米,1米=1000毫米,将单位统一,用7月23日平均降水量乘上该地区的土地面积,类似于长方体,用底面积×高即可得到体积,就是总降水量;再和4000万立方米比较即可。
【详解】1000平方千米=1000000000平方米
220毫米=0.22米
0.22×1000000000=220000000(立方米)
220000000立方米=22000万立方米
22000万立方米>4000万立方米
答:这一天整个地区的降水量能满足一年的绿化用水量。
【点睛】完成本题要细心,注意前后单位的不同及单位之间的换算。
26.(1)见详解;(2)50;(3)建议老师少留一些作业;建议减少看电视时间,增加锻炼时间
【分析】(1)条形统计图是用一个单位长度表示一定的数量,根据数量的多少画成长短不同的直条,然后把这些直条按一定的顺序排列起来。从条形统计图中很容易看出各种数量的多少,直条越长表示数量越多,直条越短表示数量越少。条形统计图一般简称条形图,也叫长条图或直条图。
(2)做作业时间最长是300分钟,图中最高是6个格,300÷6=50,每个格可表示50分钟。
(3)做作业时间最长可建议老师少留一些作业;看电视时间过长,可建议减少看电视时间,增加锻炼时间(答案不唯一)。
【详解】(1)
(2)统计图中1小格表示(50)。
(3)建议老师少留一些作业;建议减少看电视时间,增加锻炼时间。
【点睛】条形统计图的特点是能够使人们一眼看出各个数据的大小,易于比较数据之间的差别,能清楚地表示出数量的多少。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
小升初常考易错卷(试题)2023-2024学年数学六年级下册人教版
一、选择题
1.下图中共有( )条线段。
A.8 B.10 C.5 D.4
2.一个三位数,既是2、3的倍数,也是5的倍数,这个数最小是( )。
A.120 B.102 C.105 D.150
3.如果甲×0.25=乙÷0.25(甲、乙都不为0),那么甲( )乙。
A.> B.= C.< D.无法确定
4.圆柱的底面半径和高都扩大到原来的2倍,它的体积扩大到原来的( )倍。
A.2 B.4 C.6 D.8
5.甲住一楼,乙住三楼,丙住五楼。昨天下午,甲先到乙家,等乙扫完地后他们去找丙;刚上五楼就遇到了丙,于是三人立即一起下楼去玩。下面( )比较准确地描述了甲的活动。
A. B.
C. D.
6.下列说法中,正确的有( )句。
①用四个圆心角为90°的扇形,一定可以拼成一个圆。
②修一条公路,如果由甲工程队单独修,65天可以完成;如果由乙工程队单独修,75天可以完成。现在由甲、乙两个工程队合修,40天一定能修完。
③在一块长2米、宽1.6米的长方形铁板上,最多能截取40个半径是2分米的圆形铁板。
④水果店的香蕉10月第一周比上一周涨价10%,第二周比第一周涨价10%,两周以来共涨价20%。
A.3 B.2 C.1 D.0
二、填空题
7.六(1)班有38人,他们中至少有( )人在同一个月过生日。
8.在括号里填上合适的数或单位。
2460米=( )千米;1时20分=( )分;2公顷=( )平方米。
9.一个长6cm,宽4cm的长方形按5∶1放大,得到的图形面积是( )cm2。
10.一块长方形的地,长60米,宽40米,用1∶100的比例尺把它画在图纸上,图纸上这个长方形的周长是( )厘米。
11.把一根总长6m的圆柱形木料截成3段小圆柱,表面积比原木料增加12.4m2,这根圆柱形木料的体积是( )m3。
12.如图,两个同心圆中间有一个正方形,正方形的面积是10平方厘米,外圆的面积是( )平方厘米,外圆的面积与内圆的面积比是( )∶( )。
三、判断题
13.如果一个长方体四个面完全一样,那么另外两个面是正方形。( )
14.圆柱的体积一定,圆柱的高与底面积成正比例关系。( )
15.一个三角形3个内角的度数比是1∶4∶5,那么这一定是个直角三角形。( )
16.a是一个整数,它的倒数一定是。( )
17.如果a×=b×80%(a,b均不为),那么a∶b=6∶5。( )
四、计算题
18.直接等结果。
3.5÷0.07= 10÷10%= 10-10%=
19.求未知数。
20.怎样简便就怎样算。
(1) (2) (3) (4)
21.计算下图中阴影部分的面积。
五、解答题
22.王老师用“集星卡”奖励学生,10个星星卡可以换4个皇冠卡。妙妙有35个星星卡可以换几个皇冠卡?(用比例解答)
23.小明养成了喜欢读书的好习惯。妈妈给他买回一本课外书,第一天看了,第二天看了95页,第三天又看了,正好看完。这本书共有多少页?
24.为了鼓励市民节约用水,某市采用了分段计费的方式,收费标准如下表:
每月用水量 收费标准
第一阶梯 0-17吨(含) 3.4元/吨
第二阶梯 超过17吨的部分 5.3元/吨
(1)小丽家本月用水15吨,需要交水费多少元?
(2)小涛家本月交水费79元,他家这个月用了多少吨水?
25.一定时间内,降落在水平地面上的水,在未经蒸发、渗漏、流失情况下所累积的高度称为降雨量(通常以毫米作单位)。测定降雨量常用的容器是量筒和雨量器。我国气象规定,按24小时降水量为标准,降水级别如下表。某地区的土地面积大约是1000平方千米,每年用于绿化用水4000万立方米。2021年7月23日该地区的日平均降雨量是220毫米,这一天整个地区的降水量能满足一年的绿化用水量吗?
级别 小雨 中雨 大雨 暴雨 大暴雨 特大暴雨
降水量/mm 10以下 10~24.9 25~49.9 50~99.9 100-199.9 200以上
26.为了解新冠疫情防控期间学生居家学习情况,学校对四年级学生周一至周五课余时间利用情况进行了调查,平均每个学生各项活动所用时间如下表:
项目 做作业 阅读 锻炼 做家务 看电视
平均时间/分 300 125 50 25 190
(1)请根据表中的数据,完成上面的统计图。
(2)统计图中1小格表示( )。
(3)你有什么好的建议吗?(至少提两条)
参考答案:
1.B
【分析】含2个端点的线段有4条,含3个端点的线段有3条,含4个端点的线段有2条,含5个端点的线段有1条,依此计算出线段的总条数即可。
【详解】4+3+2+1=10(条),即图中共有10条线段。
故答案为:B
【点睛】熟练掌握线段的特点是解答此题的关键。
2.A
【分析】个位数字是0或者5的数,是5的倍数,根据2的特征,个位数字只能为0,这个三位数三个数位上的数字之和是3的倍数,那么这个数就是3的倍数,据此综合判断即可。
【详解】由分析可得:
该三位数既满足2、3、5倍数特征,又要求最小,所以百位上的数字是1,同时个位上的数字是0,此时百位和个位的数字之和为:
1+0=1
十位上的数字可以是2、5、8,满足三位数最小,所以十位上的数字是2,即该三位数为120,
各个数位的和为:
1+2+0
=3+0
=3
满足3的倍数,同时也满足2和5的倍数。
故答案为:A
【点睛】本题考查了2、3和5的倍数特征,该数是2、3和5的倍数,也就是既要符合2、3的倍数特征,也要符合5的倍数特征,缺一不可。
3.A
【分析】假设甲×0.25=乙÷0.25=1(甲数、乙数都不为0),则甲数=4、乙数=0.25,由此即可得出甲数、乙数的大小。
【详解】假设甲×0.25=乙÷0.25=1(甲数、乙数都不为0)
则甲数=4、乙数=0.25
因为4>0.25
则甲数>乙数
故答案为:A
【点睛】本题运用假设法,分别求出甲数、乙数的值,再比较大小,做出选择。
4.D
【分析】根据圆柱特征,圆柱底面是一个圆,圆的面积公式为:S=r2,圆柱体积公式:V=Sh,由此可得出圆柱体积公式可以表示为:V=r2h,圆柱的底面半径和高都扩大到原来的2倍,根据积的变化规律:两数相乘,其中一个因数乘m或者除以m(0除外),另一个因数乘n或者除以n(0除外),积就乘mn或者除以mn(0除外),据此判断即可。
【详解】由分析可得:
因为V=r2h,因数r扩大到原来的2倍,则r2扩大到原来的倍数为:2×2=4,另一个因数h扩大到原来的2倍,则体积扩大的倍数为:
4×2=8
即体积扩大到原来的8倍。
故答案为:D
【点睛】本题考查了圆柱体积公式的应用,以及积的变化规律的应用。
5.B
【分析】首先甲家在一楼,所以在0时,甲的楼层为0,甲先到乙家,等乙扫完地后,所以在上升一个高度后要有横着的一段时间,等乙扫完地后,他们去找丙,楼层高度再增加,刚上五楼就遇到丙,于是三人立即一起下楼去玩,那么没有停留,没有横着的时间,楼层高度在下降直至为0。据此解答。
【详解】根据分析可知,较准确地描述了甲的活动的折线统计图是:
故答案为:B
【点睛】解答此题的关键是根据题意分析折线统计图,进而得出答案。
6.C
【分析】①半径决定圆的大小,如果半径不一样,扇形无法拼成一个圆;
②把这项工程看作单位“1”,甲工程队单独修,65天可以完成,甲每天修,乙工程队单独修,75天可以完成,乙每天修,根据工作时间=工作总量÷工作效率和,1÷(+)即可求出两队合作需要的天数;
③先把长和宽的单位化为分米,然后用除法计算长有多少(2×2)分米,宽有多少个(2×2)分米,然后根据乘法计算出最多可以截取多少个半径是2分米的圆形铁板;
④把上一周香蕉的价格看作单位“1”,已知第一周比上一周涨价10%,则第一周的价格是上一周的(1+10%),再把第一周的价格看作单位“1”,又已知第二周比第一周涨价10%,则第二周的价格是第一周的(1+10%),根据百分数乘法的意义,用1×(1+10%)×(1+10%)即可求出第二周的价格,再根据求一个数比另一个数多百分之几,用相差数除以另一个数再×100%,则用第二周的价格减去上一周的价格,然后用它们的差除以上一周的价格再乘100%,据此求出两周涨价的幅度;
【详解】①半径不能确定是否一样,那就说明扇形的大小不一样,就不一定可以拼成一个圆,所以原题说法错误;
②1÷(+)
=1÷
≈34.8(天)
所以原题说法正确;
③2米=20分米
1.6米=16分米
2×2=4(分米)
直径是4分米,
长可以截取20÷4=5(个)
宽可以截取16÷4=4(个)
5×4=20(个)
所以原题说法错误。
④[1×(1+10%)×(1+10%)-1]÷1×100%
=[1×1.1×1.1-1] ÷1×100%
=[1.21-1] ÷1×100%
=0.21÷1×100%
=21%
原题说法错误。
由此可知正确的有1句。
故答案为:C
【点睛】本题考查了工程问题、百分数的应用以及剪拼问题等,结合题意分析解答即可。
7.4
【分析】在此类抽屉问题中,至少数=被分配的物体数除以抽屉数的商+1(有余的情况下)。在本题中,被分配的物体数是38,抽屉数是12(一年有12个月),据此计算即可。
【详解】38÷12=3(人)……2(人)
3+1=4(人)
六(1)班有38人,他们中至少有4人在同一个月过生日。
【点睛】抽屉原理问题的解答思路是:要从最不利情况考虑,准确地建立抽屉和确定元素的总个数,然后根据“至少数=元素的总个数÷抽屉的个数+1(有余数的情况下)”解答。
8. 2.46 80 20000
【分析】1千米=1000米,1时=60分,1公顷=10000平方米,据此进率,根据单位之间的换算,大单位换算成小单位要乘它们之间的进率;小单位换算成大单位要除以它们之间的进率。
【详解】2460米=2.46千米
1时20分=80分
2公顷=20000平方米
【点睛】本题考查了长度单位及面积单位的换算。
9.600
【分析】因为按5∶1放大,所以长方形的长是6×5=30(cm),宽是4×5=20(cm),根据长方形的面积=长×宽,求出扩大后的长方形的面积即可。
【详解】6×5=30(cm)
4×5=20(cm)
30×20=600(cm2)
得到的图形的面积是600cm2。
【点睛】此题考查的图形的放大与缩小,求出放大后的长方形的长和宽,是解答此题的关键。
10.200
【分析】根据比例尺先求图上长方形的长,再求图上长方形的宽,最后根据长方形周长的计算公式计算长方形的周长。
【详解】因为60米=6000厘米,40米=4000厘米
则6000×=60(厘米)
4000×=40(厘米)
(60+40)×2=100×2=200(厘米)
所以图纸上这个长方形的周长是200厘米。
【点睛】重点是将长方形的长和宽进行单位换算。
11.18.6
【分析】根据圆柱的切割特点可知,切成3段后,表面积比原来增加了4个圆柱的底面的面积,由此利用增加的表面积12.4m2除以4即可得出圆柱的一个底面的面积,再利用圆柱的体积公式:V=Sh,即可求出这根木料的体积。
【详解】12.4÷4×6
=3.1×6
=18.6(m3)
所以,这根圆柱形木料的体积是18.6m3。
【点睛】抓住圆柱的切割特点和增加的表面积,先求出圆柱的底面积是解决此类问题的关键。
12. 15.7 2 1
【分析】因为正方形面积是边长的平方,正方形的边长又是内圆的直径,正方形的对角线又是外圆的直径,由此可求出内外圆的面积。
【详解】解:设正方形的边长为a厘米,a×a=10平方厘米
S内圆=3.14
=7.85(平方厘米)
设外圆半径为r厘米。
2r×r÷2×2=10
2r×r=10
r×r=5
S外圆=3.14×r×r
=3.14×5
=15.7(平方厘米)
15.7∶7.85
=(15.7÷7.85)∶(7.85÷7.85)
=2∶1
【点睛】本学生题主要考查了学生的观察能力,以及对圆与正方形特征的掌握。
13.√
【分析】长方体中如有两个面是正方形,那么这两个面一定是相对的面,这两个相对的面上的8条棱长度一定相等,剩下的也就是4个长方形不在正方形面上的4条棱也相等,所以一个长方体中有四个面完全一样,那么另外两个面一定是正方形。
【详解】假如长方体中两个正方形面是左右面,那么这个长方体的宽和高的长度相等,进而可得出4个长方形面的宽都相等,又由于剩下的4条长相等,所以一个长方体中有四个面完全一样,那么另外两个面是正方形;
故答案为:√
【点睛】此题考查的长方体是一种特殊的长方体,需要记住:“有两个面是正方形的长方体,另外四个长方形的面一定完全相同”这个结论,现实生活中很多包装盒都是做成这种形状。
14.×
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例。
【详解】底面积×高=圆柱的体积(一定)
乘积一定,那么圆柱的高与底面积成反比例关系。
原题说法错误。
故答案为:×
【点睛】掌握正、反比例的意义及辨识方法是解题的关键。
15.√
【分析】三角形3个内角的度数比是1∶4∶5,进而可得最大角的度数占三角形内角和的,三角形的内角和是180°,接下来利用乘法的意义,按照求一个数的几分之几是多少的方法,即可求出这个三角形的最大角的度数,再去判断三角形的类型。
【详解】180°×
=180°×
=90°
最大角是90°,有一个角是直角的三角形是直角三角形。
故答案为:√
【点睛】此题重点考查对比的意义的理解和根据角对三角形分类的方法。
16.×
【分析】根据乘积是1的两个数互为倒数,举例说明即可。
【详解】0是整数,但是0没有倒数。
故答案为:×
【点睛】找非0自然数的倒数,可以用1除以这个数。
17.√
【分析】比例的基本性质:外项之积=内项之积,所以如果a×=b×80%,则a∶b=80%∶,再把百分数化成分数,最后进行化简分数比,化简时把比号改为除号,用求比值的方法进行化简即可。
【详解】因为a×=b×80%
所以a∶b=80%∶=∶==6∶5
故答案为:√
【点睛】掌握比例的基本性质和分数比的化简方法是关键。
18.50;;9.9;0.65;
0.2;;;0.01;
【详解】略
19.;;
【分析】根据比例的性质,将原式化成,然后根据等式的性质,方程两边同时除以;
将原式化简成,然后根据等式的性质,方程两边同时除以1.25;
根据比例的性质,将原式化成,然后根据等式的性质,方程两边同时除以7.2。
【详解】
解:
解:
解:
20.(1);(2);(3)6;(4)3
【分析】(1)先把分数除法化为分数乘法,再利用乘法结合律简便计算;
(2)先把87化为(88-1),再利用乘法分配律简便计算;
(3)先把分数除法化为分数乘法,再利用乘法分配律简便计算;
(4)利用乘法分配律简便计算。
【详解】(1)
=
=
=
=
(2)
=
=
=
=
(3)
=
=
=
=6
(4)
=
=
=3
21.28()
【分析】阴影部分是一个平行四边形,它的高和三角形的高相等,据公式:三角形的面积=底×高÷2,推出三角形的高=三角形的面积×2÷底,再利用公式:平行四边形的面积=底×高,据此求出阴影部分的面积即可。
【详解】21×2÷6×4
=42÷6×4
=7×4
=28()
【点睛】知道阴影部分的高和三角形的高相等,根据三角形面积公式计算出高,这是解决此题的关键。
22.14个
【分析】根据题意可知,星星卡的个数和皇冠卡的比值一定,因此星星卡的个数和皇冠卡成正比例,假设35个星星卡可以换x个皇冠卡,据此列方程为:35∶x=10∶4,然后解出方程即可。
【详解】解:设35个星星卡可以换x个皇冠卡。
35∶x=10∶4
10x=35×4
10x=140
x=140÷10
x=14
答:妙妙有35个星星卡可以换14个皇冠卡。
【点睛】本题考查了正比例的应用,找出题目中的等量关系,是解答此题的关键。
23.150页
【分析】根据题意可知,小明读完这本书的过程可分为3部分,①第一天看了;②第二天看了95页;③第三天又看了。其中两部分用分率表示,一部分用具体数量表示。则可知这部分具体数量占单位“1”减去其中两部分的分率,再用具体数量除以对应的分率,就得到这本书共有多少页;可列式为95÷(1--)。
【详解】95÷(1--)
=95÷(1--)
=95÷
=95×
=150(页)
答:这本书共有150页。
【点睛】本题是把整本书的页数看作单位“1”,明确单位“1”未知,用除法计算,且能够熟练计算出具体数量所对应的分率,是解题关键。
24.(1)51元;
(2)21吨
【分析】(1)当用水量为15吨时,按每吨3.4元收费,根据“总价=单价×数量”求出小丽家本月的水费;
(2)先根据“总价=单价×数量”表示用水量为17吨时需要交的水费,再表示超过17吨的部分交的水费,利用“数量=总价÷单价”计算超过17吨的用水量,最后加上17吨,据此解答。
【详解】(1)15×3.4=51(元)
答:需要交水费51元。
(2)(79-17×3.4)÷5.3+17
=(79-57.8)÷5.3+17
=21.2÷5.3+17
=4+17
=21(吨)
答:他家这个月用了21吨水。
【点睛】本题主要考查分段计费,明确不同用水量对应的收费标准是解答题目的关键。
25.能满足
【分析】根据1平方千米=1000000平方米,1米=1000毫米,将单位统一,用7月23日平均降水量乘上该地区的土地面积,类似于长方体,用底面积×高即可得到体积,就是总降水量;再和4000万立方米比较即可。
【详解】1000平方千米=1000000000平方米
220毫米=0.22米
0.22×1000000000=220000000(立方米)
220000000立方米=22000万立方米
22000万立方米>4000万立方米
答:这一天整个地区的降水量能满足一年的绿化用水量。
【点睛】完成本题要细心,注意前后单位的不同及单位之间的换算。
26.(1)见详解;(2)50;(3)建议老师少留一些作业;建议减少看电视时间,增加锻炼时间
【分析】(1)条形统计图是用一个单位长度表示一定的数量,根据数量的多少画成长短不同的直条,然后把这些直条按一定的顺序排列起来。从条形统计图中很容易看出各种数量的多少,直条越长表示数量越多,直条越短表示数量越少。条形统计图一般简称条形图,也叫长条图或直条图。
(2)做作业时间最长是300分钟,图中最高是6个格,300÷6=50,每个格可表示50分钟。
(3)做作业时间最长可建议老师少留一些作业;看电视时间过长,可建议减少看电视时间,增加锻炼时间(答案不唯一)。
【详解】(1)
(2)统计图中1小格表示(50)。
(3)建议老师少留一些作业;建议减少看电视时间,增加锻炼时间。
【点睛】条形统计图的特点是能够使人们一眼看出各个数据的大小,易于比较数据之间的差别,能清楚地表示出数量的多少。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
