小升初常考易错卷(试题)2023-2024学年数学六年级下册(重庆市适用)(含解析)
文档属性
| 名称 | 小升初常考易错卷(试题)2023-2024学年数学六年级下册(重庆市适用)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 609.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-20 21:18:14 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
小升初常考易错卷(试题)2023-2024学年数学六年级下册(重庆市适用)
一、选择题
1.一个一位小数,十位上的数是8,个位上的数是a,十分位上的数是b,表示这个数的式子是( )。
A.8+a+b B.8ab C.80+a+b D.以上答案都不对
2.改写成数字比例尺,正确的答案是( )。
A.1∶40 B.1∶4000000 C.1∶8000000 D.1∶12000000
3.如果规定从原点出发,向南走为正,那么﹣100m表示的意义是( )。
A.向东走100m B.向西走100m C.向北走100m D.向南走100m
4.a、b和c是三个非零自然数,且a=b×c,下面说法正确的是( )。
A.b和c是互质数 B.b和c都是a的质因数
C.b和c都是a的因数 D.b一定是c的倍数
5.某班同学去划船,他们算了一下,如果增加1条船,正好每条船坐6人;如果减少1条船,正好每条船坐9人,则该班有( )名同学。
A.32 B.36 C.40 D.48
6.如果a÷=b÷=c×(a、b、c均不为0),那a、b、c中,哪个最小?( )
A.a B.b C.c D.无法确定
二、填空题
7.在括号里填上合适的单位名称。
一个叫洋洋的小学生,他的身高大约145( ),他每天需要饮水1500( ),体育课上跑100米需要16( ),他的数学课本面积约是4( )
8.长方形有( )条对称轴,正方形有( )条对称轴,圆有( )条对称轴。
9.把5米长的铁丝平均分成8段,每段占全长的( )%,每段长( )米。
10.根据8x=3y组成一个比例x∶y=( )∶( )。找出24的因数,并利用其中的数组成比值最大的比例( )。
11.一根1米长圆柱形钢材,沿横截面截去2分米长的一段后。表面积减少了50.24平方分米。原来这根钢材的体积是( )立方分米。
12.某鞋店推出“买一送一”的活动(不同价格的两双鞋子按价格高的那双付款),王叔叔看中了两双鞋子,价格分别是300元和200元,他同时买下这两双鞋子,相当于打( )折。
三、判断题
13.把10个苹果放进三个果盘中,总有一个果盘中至少放4个苹果。( )
14.一个直角三角形,绕它的任何一边旋转一周形成的图形都是一个圆锥。( )
15.王师傅加工了100个零件,合格率是99%,如果他再加工1个合格的零件,合格率就达到了100%。( )
16.学校十月份的用电量比九月份节约了,也可以说九月份的用电量是十月份的。( )
17.如果正方形的周长等于圆的周长,那么正方形的面积一定小于圆的面积。( )
四、计算题
18.直接写得数。
19.用简便方法计算。(写出简要的计算过程)
20.解方程。
(1)1-60%x=0.4 (2)x-10=35 (3)50%x-33%x=34
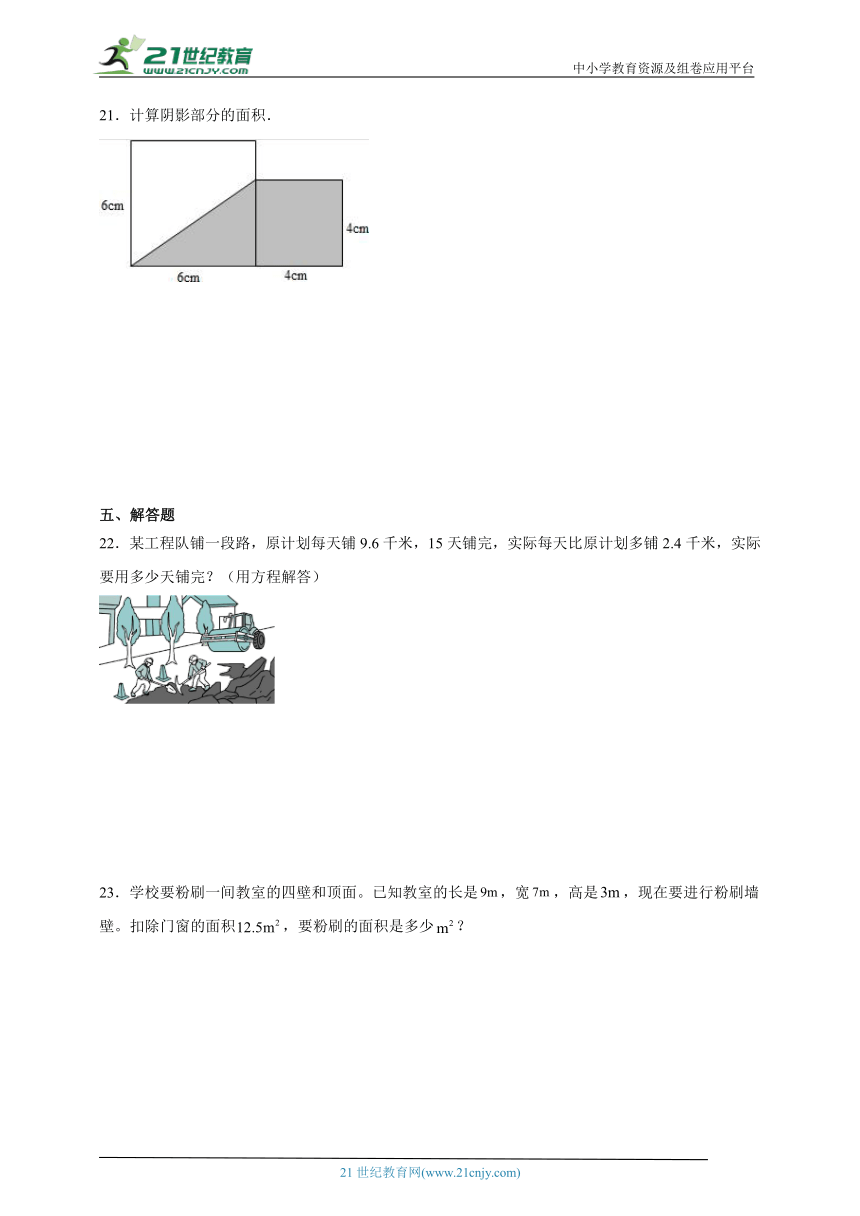
21.计算阴影部分的面积.
五、解答题
22.某工程队铺一段路,原计划每天铺9.6千米,15天铺完,实际每天比原计划多铺2.4千米,实际要用多少天铺完?(用方程解答)
23.学校要粉刷一间教室的四壁和顶面。已知教室的长是,宽,高是,现在要进行粉刷墙壁。扣除门窗的面积,要粉刷的面积是多少?
24.客车从甲地开往乙地,每小时行全程的,货车同时从乙地开往甲地,经过3小时与客车相遇,相遇时货车行了。甲、乙两地相距多少千米?
25.按要求在方格纸上画图。(每个小方格的面积表示1平方厘米)
1.用数对表示图中A点的位置是( );画出平行四边形绕A点顺时针旋转90°后的图形,旋转后C点的位置是( )。
2.按1∶2的比画出圆缩小后的图形,使得缩小后的图形与原来的圆组成一个有无数条对称轴的图形。缩小后图形的面积是原来圆面积的( )。
3.画一个面积是6平方厘米的轴对称图形,并画出对称轴。
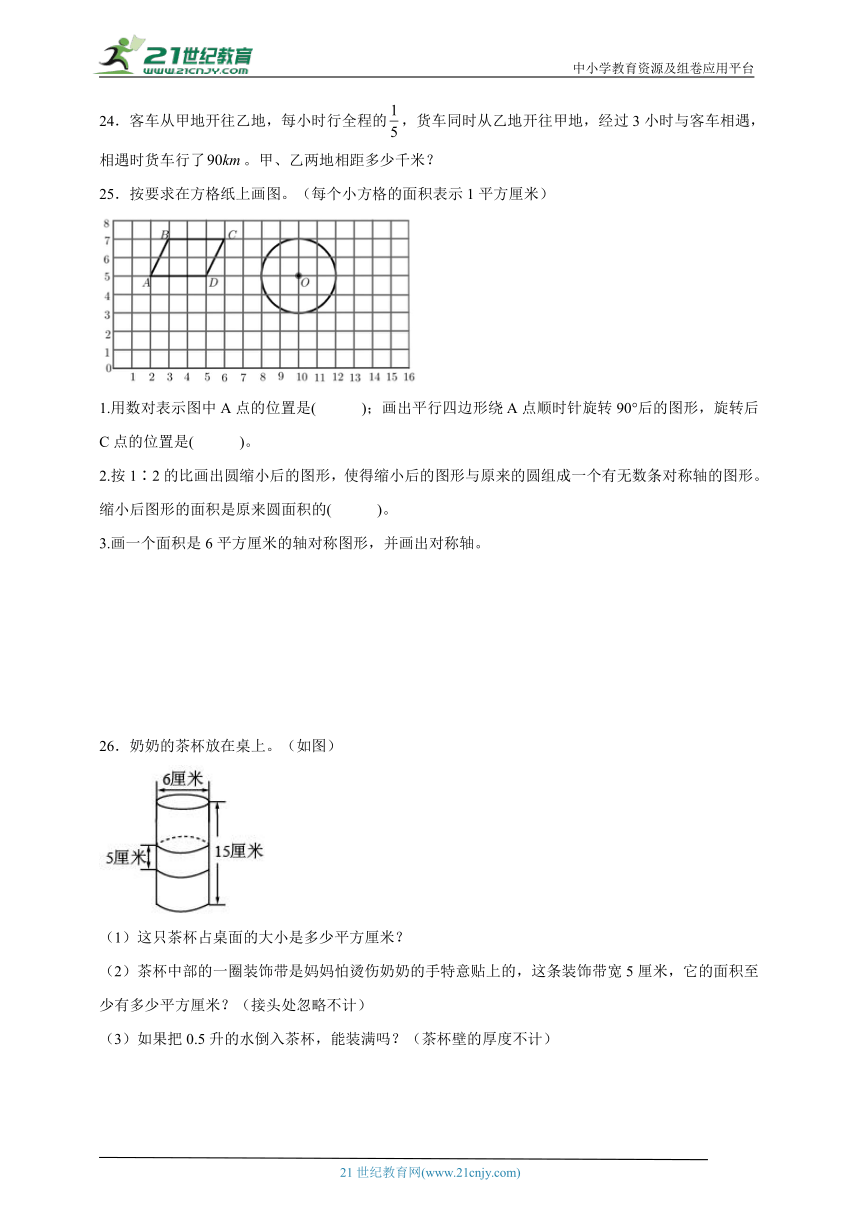
26.奶奶的茶杯放在桌上。(如图)
(1)这只茶杯占桌面的大小是多少平方厘米?
(2)茶杯中部的一圈装饰带是妈妈怕烫伤奶奶的手特意贴上的,这条装饰带宽5厘米,它的面积至少有多少平方厘米?(接头处忽略不计)
(3)如果把0.5升的水倒入茶杯,能装满吗?(茶杯壁的厚度不计)
参考答案:
1.D
【分析】十位上是几表示有几个10,个位上是几表示有几个一,十分位上是几表示有几个0.1,据此解答即可。
【详解】8×10+a+0.1b
所以这个数的式子是80+a+0.1b;
故答案为:D
【点睛】解题关键是明确每个数位上数字的意义,注意基础知识的积累。
2.B
【分析】由线段比例尺可知,图上1厘米表示实际距离40千米,比例尺=图上距离∶实际距离,据此解答。
【详解】40千米=4000000厘米,所以改成数字比例尺为:1∶4000000;
故答案为:B
【点睛】此题考查了比例尺的意义,换算单位时注意0的个数。
3.C
【分析】如果向南走记为正,那么向北走记为负,据此分析。
【详解】如果规定从原点出发,向南走为正,那么﹣100m表示的意义是向北走100m。
故答案为:C
【点睛】关键是理解正负数的意义,正负数可以表示相反意义的量。
4.C
【分析】a=b×c,b和c不一定是互质数,b和c也不一定是a的质因数,如:8=4×2;
在乘数和积都是整数的乘法算式中,积是乘数的倍数,乘数是积的因数,由此解答即可。
【详解】A.b和c不一定是互质数,原题说法错误 ;
B.b和c不一定是a的质因数,原题说法错误;
C.b和c是a的因数,a是b和c的倍数,说法正确;
D.b不一定是c的倍数,如:20=4×5,原题说法错误。
故答案为:C。
【点睛】注意因数与倍数都是表达两个数之间的关系,所以一定要说清楚谁是谁的因数,谁是谁的倍数。
5.B
【分析】无论同学们用多少条船,总人数不变。可以设计划准备的船是x条,如果增加1条船,可以乘坐的人数是(x+1)×6(人);如果减少1条船,可以乘坐的人数是(x-1)×9(人)。据此列出方程算出计划准备多少条船,再求出总人数。
【详解】解:设计划准备x条船。
(x-1)×9=(x+1)×6
9x-9=6x+6
9x-9+9=6x+6+9
9x=6x+15
9x-6x=6x+15-6x
3x=15
3x÷3=15÷3
x=5
(5+1)×6
=6×6
=36(人)
故答案为:B
【点睛】列方程解决实际问题时,有时可以不设问题为未知数。
6.C
【详解】假设a÷=b÷=c×=1,则a=,b=,c=,只有c是真分数小于1。
故答案为:C
7. 厘米 毫升 秒 平方分米
【分析】根据实际生活与长度单位、面积单位、容积单位的联系,填入合适的单位即可。
【详解】一个叫洋洋的小学生,他的身高大约145( 厘米 ),他每天需要饮水1500( 毫升 ),体育课上跑100米需要16( 秒 ),他的数学课本面积约是4( 平方分米 )。
【点睛】本题考查选择合适的单位,联系生活实际是解题的关键。
8. 2 4 无数
【分析】将图形沿着一条直线对折,如果直线两侧的部分能够完全重合,折痕所在的直线叫做它的对称轴,根据对称轴定义找出各图形对称轴的数量。
【详解】长方形的对称轴:每组对边中点连线所在的直线,共有2条对称轴;
正方形的对称轴:每组对边中点连线所在的直线,对角线所在的直线,共有4条对称轴;
圆形的对称轴:将一张圆形纸片对折,折线两侧的部分可以完全重合,圆有无数条对称轴。
由上可知,长方形有2条对称轴,正方形有4条对称轴,圆有无数条对称轴。
【点睛】本题主要考查轴对称图形的认识,掌握对称轴的意义是解答题目的关键。
9. 12.5
【分析】根据分数的意义,把5米长的铁丝平均分成8段,即把这根铁丝的长度看作单位“1”,将它平均分成8份,那么每份长度就是全长的,将分数化成百分数。
每段的长度=铁丝总长度÷所分的段数。
【详解】1÷8==12.5%,5÷8=(米)
每段占全长的12.5%,每段长米。
【点睛】求一个数是另一个数的几分之几/百分之几,用除法。
10. 3 8 24∶2=12∶1
【分析】(1)将乘积形式的等式改写成比例时,要根据比例的基本性质:两外项积等于两内项积,在8x=3y中,8、x是外项,3、y就是内项,由此即可写出比例:x∶y=3∶8;
(2)根据找一个数的因数的方法,可以一对一对地找,最小的是1,最大的是它本身;然后根据求比值的方法和比例的意义,写出两个比值最大的比,进而组成比例即可。
【详解】(1)因为8x=3y,所以x∶y=3∶8;
(2)24的因数有:1,2,3,4,6,8,12,24。
比值最大的比例为24∶2=12∶1。
【点睛】此题主要考查了比例的基本性质的应用及求一个数的因数,从24的因数中可以写出几个不同的比例是解题关键。
11.502.4
【分析】截去2分米的一段后,表面积减少的部分正好是这段2分米钢材的侧面积,用侧面积除以高,求出底面圆的周长,利用圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,求出底面半径,再根据圆柱的体积公式:体积=底面积×高,计算出体积。
【详解】1米=10分米
50.24÷2÷3.14÷2=4(分米)
3.14×4×4×10=502.4(立方分米)
原来这根钢材的体积是502.4立方分米。
【点睛】本题考查圆柱表面积及体积的计算方法,根据表面积减少情况计算出原钢材的底面半径,再结合钢材的长进一步计算出体积,注意单位名数的换算。
12.六
【分析】用两双鞋子中价格高的鞋的价格除以两双鞋子价格和即可解答。
【详解】300÷(300+200)×100%
=300÷500×100%
=0.6×100%
=60%
=六折
相当于打(六)折。
【点评】解答此题的关键需明确是原价的百分之几十即打几折。
13.√
【分析】从最坏的情况考虑,如果三个果盘中各放3个苹果,那么剩下的1个苹果无论放在哪个盘子里,总有一个果盘中至少放4个苹果。
【详解】10÷3=3……1,3+1=4,所以把10个苹果放进三个果盘中,总有一个果盘中至少放4个苹果。原题说法正确。
故答案为:√。
【点睛】此题考查的是抽屉原理,一定要从从最不利情况考虑。
14.×
【分析】绕着直角三角形的一条直角边旋转一周会形成一个圆锥,绕着直角三角形的斜边旋转一周不会形成一个圆锥。
【详解】根据分析可知,原题说法错误。
故答案为:×。
【点睛】本题考查了学生对立体图形的空间想象能力及分析问题、解决问题的能力。
15.×
【分析】合格率=合格零件个数÷零件总数×100%,再加工1个合格零件后,合格零件数是(100×99%+1)个,零件总数是(100+1)个,计算出合格率后再判断即可。
【详解】(100×99%+1)÷(100+1)×100%
=100÷101×100%
≈99%
合格率达到99%,原题说法错误。
故答案为:×。
【点睛】考查了合格率,学生要理解并掌握公式。
16.×
【分析】学校十月份的用电量比九月份节约了,九月份用电量是单位“1”,十月份用电量是九月份的1-10%,求九月份是十月份的百分之几,用九月份用电量÷十月份用电量。
【详解】1÷(1-10%)
=1÷0.9
≈1.111
=111.1%
九月份用电量是十月份的111.1%,所以原题说法错误。
【点睛】本题考查了百分数复合应用题,关键是确定单位“1”。
17.√
【分析】周长相等的圆和正方形,根据圆的面积公式S=πr2,正方形的面积公式:边长×边长,设圆和正方形的周长为4π,求出它们的面积进行比较即可。
【详解】设圆和正方形的周长为4π,则圆的半径为2,正方形的边长为π
圆的面积:π×2×2=4π
正方形的面积:π×π=π2
正方形的面积和圆的面积的比是:π2∶4π=π∶4;
所以正方形的面积小于圆的面积
故答案为:√。
【点睛】此题主要考查周长相等的圆和正方形的面积的比较,灵活掌握正方形和圆的面积公式,发现并掌握规律,从而较好的解决这类问题。
18.;20;0;
20;10;;6
【详解】略
19.20;8;35
【分析】(1)运用乘法分配律进行计算即可。
(2)把除以化为乘80%,然后运用乘法分配律进行计算即可。
(3)运用乘法结合律进行计算即可。
【详解】
=
=
=
=
=
=
=8
=
=
=35
20.(1)x=1;(2)x=180;(3)x=200
【分析】(1)根据等式的性质,方程两边同时加60%x,再同时减去0.4,最后同时除以60%即可;
(2)根据等式的性质,方程两边同时加10,再同时除以即可;
(3)先化简方程,再根据等式的性质,方程两边同时除以17%即可。
【详解】(1)1-60%x=0.4
解:1-60%x+60%x=0.4+60%x
1=0.4+60%x
0.4+60%x-0.4=1-0.4
60%x=0.6
60%x÷60%=0.6÷60%
x=1
(2)x-10=35
解:x-10+10=35+10
x=45
x÷=45÷
x×4=45×4
x=180
(3)50%x-33%x=34
解:17%x=34
17%x÷17%=34÷17%
x=200
21.28平方厘米
【详解】(4+6+4)×4÷2,
=14×4÷2,
=28(平方厘米);
答:阴影部分的面积是28平方厘米.
【点睛】由图意可知:阴影部分是一个梯形,上底、下底和高已知,利用梯形的面积公式即可求解.
22.12天
【分析】设实际要用x天铺完,根据实际每天铺的长度×天数=计划每天铺的长度×天数,列出方程解答即可。
【详解】解:设实际要用x天铺完。
(2.4+9.6)x=9.6×15
12x÷12=144÷12
x=12
答:实际要用12天铺完。
【点睛】本题考查了列方程解决问题,关键是找到等量关系。
23.146.5
【分析】求出教室前、后、左、右、上面,5个面的面积和,减去门窗面积即可。
【详解】9×7+9×3×2+7×3×2-12.5
=63+54+42-12.5
=146.5(平方米)
答:要粉刷的面积是146.5。
【点睛】关键是掌握长方体表面积求法,长方体表面积=(长×宽+长×高+宽×高)×2。
24.千米
【分析】根据题意可知,3小时客车行驶了全长的×3,则货车行了全长的,正好是90千米,再根据分数除法的意义解答即可。
【详解】
=1-
=;
(千米);
答:甲、乙两地相距千米。
【点睛】求出货车行了全长的几分之几是解答本题的关键。
25. (2,5); (4,1)
1.2.3.图形略
【分析】1.在数对中,横坐标表示第一个数字,纵坐标表示第二个数字;点A的位置不变,其它各部分均绕点A顺时针旋转90°,作出旋转后的图形,进而表示出C点的位置。
2.缩小后的圆与原来的圆圆心位置相同,按1∶2的比缩小,则半径是原来圆半径的 ,缩小后后图形的面积是原来圆面积的()2。
3.可画一个长是3厘米,宽是2厘米的长方形,合理即可。
【详解】1.用数对表示图中A点的位置是(2,5);旋转后C点的位置是(4,1)。
2.缩小后图形的面积是原来圆面积的×= 。
1.2.3作图如下:
(3答案不唯一)
【点睛】此题考查了图形的放缩、作旋转后的图形、轴对称图形以及数对的综合应用。
26.(1)平方厘米;
(2)平方厘米;
(3)不能
【分析】(1)占桌面的面积也就是圆柱的底面积,根据圆的面积S=πr2,代入数据计算即可。
(2)装饰带的面积=底面周长×宽度;
(3)根据圆柱的体积V=πr2h,求出茶杯的容积与0.5升比较即可。
【详解】(1)
=9×3.14
=28.26(平方厘米)
答:这只茶杯占桌面的大小是28.26平方厘米。
(2)
=3.14×30
=94.2(平方厘米)
答:面积至少有平方厘米。
(3)
=3.14×9×15
=28.26×15
=423.9(立方厘米)
423.9立方厘米=0.4239升
答:不能装满。
【点睛】此题考查了圆柱体的相关应用,明确圆柱的体积和侧面积计算公式,并能灵活运用是解题关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
小升初常考易错卷(试题)2023-2024学年数学六年级下册(重庆市适用)
一、选择题
1.一个一位小数,十位上的数是8,个位上的数是a,十分位上的数是b,表示这个数的式子是( )。
A.8+a+b B.8ab C.80+a+b D.以上答案都不对
2.改写成数字比例尺,正确的答案是( )。
A.1∶40 B.1∶4000000 C.1∶8000000 D.1∶12000000
3.如果规定从原点出发,向南走为正,那么﹣100m表示的意义是( )。
A.向东走100m B.向西走100m C.向北走100m D.向南走100m
4.a、b和c是三个非零自然数,且a=b×c,下面说法正确的是( )。
A.b和c是互质数 B.b和c都是a的质因数
C.b和c都是a的因数 D.b一定是c的倍数
5.某班同学去划船,他们算了一下,如果增加1条船,正好每条船坐6人;如果减少1条船,正好每条船坐9人,则该班有( )名同学。
A.32 B.36 C.40 D.48
6.如果a÷=b÷=c×(a、b、c均不为0),那a、b、c中,哪个最小?( )
A.a B.b C.c D.无法确定
二、填空题
7.在括号里填上合适的单位名称。
一个叫洋洋的小学生,他的身高大约145( ),他每天需要饮水1500( ),体育课上跑100米需要16( ),他的数学课本面积约是4( )
8.长方形有( )条对称轴,正方形有( )条对称轴,圆有( )条对称轴。
9.把5米长的铁丝平均分成8段,每段占全长的( )%,每段长( )米。
10.根据8x=3y组成一个比例x∶y=( )∶( )。找出24的因数,并利用其中的数组成比值最大的比例( )。
11.一根1米长圆柱形钢材,沿横截面截去2分米长的一段后。表面积减少了50.24平方分米。原来这根钢材的体积是( )立方分米。
12.某鞋店推出“买一送一”的活动(不同价格的两双鞋子按价格高的那双付款),王叔叔看中了两双鞋子,价格分别是300元和200元,他同时买下这两双鞋子,相当于打( )折。
三、判断题
13.把10个苹果放进三个果盘中,总有一个果盘中至少放4个苹果。( )
14.一个直角三角形,绕它的任何一边旋转一周形成的图形都是一个圆锥。( )
15.王师傅加工了100个零件,合格率是99%,如果他再加工1个合格的零件,合格率就达到了100%。( )
16.学校十月份的用电量比九月份节约了,也可以说九月份的用电量是十月份的。( )
17.如果正方形的周长等于圆的周长,那么正方形的面积一定小于圆的面积。( )
四、计算题
18.直接写得数。
19.用简便方法计算。(写出简要的计算过程)
20.解方程。
(1)1-60%x=0.4 (2)x-10=35 (3)50%x-33%x=34
21.计算阴影部分的面积.
五、解答题
22.某工程队铺一段路,原计划每天铺9.6千米,15天铺完,实际每天比原计划多铺2.4千米,实际要用多少天铺完?(用方程解答)
23.学校要粉刷一间教室的四壁和顶面。已知教室的长是,宽,高是,现在要进行粉刷墙壁。扣除门窗的面积,要粉刷的面积是多少?
24.客车从甲地开往乙地,每小时行全程的,货车同时从乙地开往甲地,经过3小时与客车相遇,相遇时货车行了。甲、乙两地相距多少千米?
25.按要求在方格纸上画图。(每个小方格的面积表示1平方厘米)
1.用数对表示图中A点的位置是( );画出平行四边形绕A点顺时针旋转90°后的图形,旋转后C点的位置是( )。
2.按1∶2的比画出圆缩小后的图形,使得缩小后的图形与原来的圆组成一个有无数条对称轴的图形。缩小后图形的面积是原来圆面积的( )。
3.画一个面积是6平方厘米的轴对称图形,并画出对称轴。
26.奶奶的茶杯放在桌上。(如图)
(1)这只茶杯占桌面的大小是多少平方厘米?
(2)茶杯中部的一圈装饰带是妈妈怕烫伤奶奶的手特意贴上的,这条装饰带宽5厘米,它的面积至少有多少平方厘米?(接头处忽略不计)
(3)如果把0.5升的水倒入茶杯,能装满吗?(茶杯壁的厚度不计)
参考答案:
1.D
【分析】十位上是几表示有几个10,个位上是几表示有几个一,十分位上是几表示有几个0.1,据此解答即可。
【详解】8×10+a+0.1b
所以这个数的式子是80+a+0.1b;
故答案为:D
【点睛】解题关键是明确每个数位上数字的意义,注意基础知识的积累。
2.B
【分析】由线段比例尺可知,图上1厘米表示实际距离40千米,比例尺=图上距离∶实际距离,据此解答。
【详解】40千米=4000000厘米,所以改成数字比例尺为:1∶4000000;
故答案为:B
【点睛】此题考查了比例尺的意义,换算单位时注意0的个数。
3.C
【分析】如果向南走记为正,那么向北走记为负,据此分析。
【详解】如果规定从原点出发,向南走为正,那么﹣100m表示的意义是向北走100m。
故答案为:C
【点睛】关键是理解正负数的意义,正负数可以表示相反意义的量。
4.C
【分析】a=b×c,b和c不一定是互质数,b和c也不一定是a的质因数,如:8=4×2;
在乘数和积都是整数的乘法算式中,积是乘数的倍数,乘数是积的因数,由此解答即可。
【详解】A.b和c不一定是互质数,原题说法错误 ;
B.b和c不一定是a的质因数,原题说法错误;
C.b和c是a的因数,a是b和c的倍数,说法正确;
D.b不一定是c的倍数,如:20=4×5,原题说法错误。
故答案为:C。
【点睛】注意因数与倍数都是表达两个数之间的关系,所以一定要说清楚谁是谁的因数,谁是谁的倍数。
5.B
【分析】无论同学们用多少条船,总人数不变。可以设计划准备的船是x条,如果增加1条船,可以乘坐的人数是(x+1)×6(人);如果减少1条船,可以乘坐的人数是(x-1)×9(人)。据此列出方程算出计划准备多少条船,再求出总人数。
【详解】解:设计划准备x条船。
(x-1)×9=(x+1)×6
9x-9=6x+6
9x-9+9=6x+6+9
9x=6x+15
9x-6x=6x+15-6x
3x=15
3x÷3=15÷3
x=5
(5+1)×6
=6×6
=36(人)
故答案为:B
【点睛】列方程解决实际问题时,有时可以不设问题为未知数。
6.C
【详解】假设a÷=b÷=c×=1,则a=,b=,c=,只有c是真分数小于1。
故答案为:C
7. 厘米 毫升 秒 平方分米
【分析】根据实际生活与长度单位、面积单位、容积单位的联系,填入合适的单位即可。
【详解】一个叫洋洋的小学生,他的身高大约145( 厘米 ),他每天需要饮水1500( 毫升 ),体育课上跑100米需要16( 秒 ),他的数学课本面积约是4( 平方分米 )。
【点睛】本题考查选择合适的单位,联系生活实际是解题的关键。
8. 2 4 无数
【分析】将图形沿着一条直线对折,如果直线两侧的部分能够完全重合,折痕所在的直线叫做它的对称轴,根据对称轴定义找出各图形对称轴的数量。
【详解】长方形的对称轴:每组对边中点连线所在的直线,共有2条对称轴;
正方形的对称轴:每组对边中点连线所在的直线,对角线所在的直线,共有4条对称轴;
圆形的对称轴:将一张圆形纸片对折,折线两侧的部分可以完全重合,圆有无数条对称轴。
由上可知,长方形有2条对称轴,正方形有4条对称轴,圆有无数条对称轴。
【点睛】本题主要考查轴对称图形的认识,掌握对称轴的意义是解答题目的关键。
9. 12.5
【分析】根据分数的意义,把5米长的铁丝平均分成8段,即把这根铁丝的长度看作单位“1”,将它平均分成8份,那么每份长度就是全长的,将分数化成百分数。
每段的长度=铁丝总长度÷所分的段数。
【详解】1÷8==12.5%,5÷8=(米)
每段占全长的12.5%,每段长米。
【点睛】求一个数是另一个数的几分之几/百分之几,用除法。
10. 3 8 24∶2=12∶1
【分析】(1)将乘积形式的等式改写成比例时,要根据比例的基本性质:两外项积等于两内项积,在8x=3y中,8、x是外项,3、y就是内项,由此即可写出比例:x∶y=3∶8;
(2)根据找一个数的因数的方法,可以一对一对地找,最小的是1,最大的是它本身;然后根据求比值的方法和比例的意义,写出两个比值最大的比,进而组成比例即可。
【详解】(1)因为8x=3y,所以x∶y=3∶8;
(2)24的因数有:1,2,3,4,6,8,12,24。
比值最大的比例为24∶2=12∶1。
【点睛】此题主要考查了比例的基本性质的应用及求一个数的因数,从24的因数中可以写出几个不同的比例是解题关键。
11.502.4
【分析】截去2分米的一段后,表面积减少的部分正好是这段2分米钢材的侧面积,用侧面积除以高,求出底面圆的周长,利用圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,求出底面半径,再根据圆柱的体积公式:体积=底面积×高,计算出体积。
【详解】1米=10分米
50.24÷2÷3.14÷2=4(分米)
3.14×4×4×10=502.4(立方分米)
原来这根钢材的体积是502.4立方分米。
【点睛】本题考查圆柱表面积及体积的计算方法,根据表面积减少情况计算出原钢材的底面半径,再结合钢材的长进一步计算出体积,注意单位名数的换算。
12.六
【分析】用两双鞋子中价格高的鞋的价格除以两双鞋子价格和即可解答。
【详解】300÷(300+200)×100%
=300÷500×100%
=0.6×100%
=60%
=六折
相当于打(六)折。
【点评】解答此题的关键需明确是原价的百分之几十即打几折。
13.√
【分析】从最坏的情况考虑,如果三个果盘中各放3个苹果,那么剩下的1个苹果无论放在哪个盘子里,总有一个果盘中至少放4个苹果。
【详解】10÷3=3……1,3+1=4,所以把10个苹果放进三个果盘中,总有一个果盘中至少放4个苹果。原题说法正确。
故答案为:√。
【点睛】此题考查的是抽屉原理,一定要从从最不利情况考虑。
14.×
【分析】绕着直角三角形的一条直角边旋转一周会形成一个圆锥,绕着直角三角形的斜边旋转一周不会形成一个圆锥。
【详解】根据分析可知,原题说法错误。
故答案为:×。
【点睛】本题考查了学生对立体图形的空间想象能力及分析问题、解决问题的能力。
15.×
【分析】合格率=合格零件个数÷零件总数×100%,再加工1个合格零件后,合格零件数是(100×99%+1)个,零件总数是(100+1)个,计算出合格率后再判断即可。
【详解】(100×99%+1)÷(100+1)×100%
=100÷101×100%
≈99%
合格率达到99%,原题说法错误。
故答案为:×。
【点睛】考查了合格率,学生要理解并掌握公式。
16.×
【分析】学校十月份的用电量比九月份节约了,九月份用电量是单位“1”,十月份用电量是九月份的1-10%,求九月份是十月份的百分之几,用九月份用电量÷十月份用电量。
【详解】1÷(1-10%)
=1÷0.9
≈1.111
=111.1%
九月份用电量是十月份的111.1%,所以原题说法错误。
【点睛】本题考查了百分数复合应用题,关键是确定单位“1”。
17.√
【分析】周长相等的圆和正方形,根据圆的面积公式S=πr2,正方形的面积公式:边长×边长,设圆和正方形的周长为4π,求出它们的面积进行比较即可。
【详解】设圆和正方形的周长为4π,则圆的半径为2,正方形的边长为π
圆的面积:π×2×2=4π
正方形的面积:π×π=π2
正方形的面积和圆的面积的比是:π2∶4π=π∶4;
所以正方形的面积小于圆的面积
故答案为:√。
【点睛】此题主要考查周长相等的圆和正方形的面积的比较,灵活掌握正方形和圆的面积公式,发现并掌握规律,从而较好的解决这类问题。
18.;20;0;
20;10;;6
【详解】略
19.20;8;35
【分析】(1)运用乘法分配律进行计算即可。
(2)把除以化为乘80%,然后运用乘法分配律进行计算即可。
(3)运用乘法结合律进行计算即可。
【详解】
=
=
=
=
=
=
=8
=
=
=35
20.(1)x=1;(2)x=180;(3)x=200
【分析】(1)根据等式的性质,方程两边同时加60%x,再同时减去0.4,最后同时除以60%即可;
(2)根据等式的性质,方程两边同时加10,再同时除以即可;
(3)先化简方程,再根据等式的性质,方程两边同时除以17%即可。
【详解】(1)1-60%x=0.4
解:1-60%x+60%x=0.4+60%x
1=0.4+60%x
0.4+60%x-0.4=1-0.4
60%x=0.6
60%x÷60%=0.6÷60%
x=1
(2)x-10=35
解:x-10+10=35+10
x=45
x÷=45÷
x×4=45×4
x=180
(3)50%x-33%x=34
解:17%x=34
17%x÷17%=34÷17%
x=200
21.28平方厘米
【详解】(4+6+4)×4÷2,
=14×4÷2,
=28(平方厘米);
答:阴影部分的面积是28平方厘米.
【点睛】由图意可知:阴影部分是一个梯形,上底、下底和高已知,利用梯形的面积公式即可求解.
22.12天
【分析】设实际要用x天铺完,根据实际每天铺的长度×天数=计划每天铺的长度×天数,列出方程解答即可。
【详解】解:设实际要用x天铺完。
(2.4+9.6)x=9.6×15
12x÷12=144÷12
x=12
答:实际要用12天铺完。
【点睛】本题考查了列方程解决问题,关键是找到等量关系。
23.146.5
【分析】求出教室前、后、左、右、上面,5个面的面积和,减去门窗面积即可。
【详解】9×7+9×3×2+7×3×2-12.5
=63+54+42-12.5
=146.5(平方米)
答:要粉刷的面积是146.5。
【点睛】关键是掌握长方体表面积求法,长方体表面积=(长×宽+长×高+宽×高)×2。
24.千米
【分析】根据题意可知,3小时客车行驶了全长的×3,则货车行了全长的,正好是90千米,再根据分数除法的意义解答即可。
【详解】
=1-
=;
(千米);
答:甲、乙两地相距千米。
【点睛】求出货车行了全长的几分之几是解答本题的关键。
25. (2,5); (4,1)
1.2.3.图形略
【分析】1.在数对中,横坐标表示第一个数字,纵坐标表示第二个数字;点A的位置不变,其它各部分均绕点A顺时针旋转90°,作出旋转后的图形,进而表示出C点的位置。
2.缩小后的圆与原来的圆圆心位置相同,按1∶2的比缩小,则半径是原来圆半径的 ,缩小后后图形的面积是原来圆面积的()2。
3.可画一个长是3厘米,宽是2厘米的长方形,合理即可。
【详解】1.用数对表示图中A点的位置是(2,5);旋转后C点的位置是(4,1)。
2.缩小后图形的面积是原来圆面积的×= 。
1.2.3作图如下:
(3答案不唯一)
【点睛】此题考查了图形的放缩、作旋转后的图形、轴对称图形以及数对的综合应用。
26.(1)平方厘米;
(2)平方厘米;
(3)不能
【分析】(1)占桌面的面积也就是圆柱的底面积,根据圆的面积S=πr2,代入数据计算即可。
(2)装饰带的面积=底面周长×宽度;
(3)根据圆柱的体积V=πr2h,求出茶杯的容积与0.5升比较即可。
【详解】(1)
=9×3.14
=28.26(平方厘米)
答:这只茶杯占桌面的大小是28.26平方厘米。
(2)
=3.14×30
=94.2(平方厘米)
答:面积至少有平方厘米。
(3)
=3.14×9×15
=28.26×15
=423.9(立方厘米)
423.9立方厘米=0.4239升
答:不能装满。
【点睛】此题考查了圆柱体的相关应用,明确圆柱的体积和侧面积计算公式,并能灵活运用是解题关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
