10.1相交线同步练习题(含解析)沪科版七年级数学下册
文档属性
| 名称 | 10.1相交线同步练习题(含解析)沪科版七年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 168.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-20 06:55:42 | ||
图片预览




文档简介
沪科版七年级数学下册《10.1相交线》同步练习题
一.选择题
1.若四条直线在平面内交点的个数为a,则a的可能取值有( )
A.3个 B.4个 C.5个 D.6个
2.平面内两两相交的8条直线,其交点个数最少为m个,最多为n个,则m+n等于( )
A.16 B.18 C.29 D.28
3.下列说法中正确的有( )
①过两点有且只有一条直线;
②连接两点的线段叫做两点的距离;
③平角是一条直线;
④若∠AOC=2∠BOC,则OB是∠AOC的平分线;
⑤三条直线两两相交,只有1个交点.
A.1个 B.2个 C.3个 D.4个
4.如图,直线AB、CD、EF相交于O,图中对顶角共有( )
A.3对 B.4对 C.5对 D.6对
5.如图,直线AB、CD相交于点O,作射线OE,则图中邻补角有( )
A.4对 B.6对 C.7对 D.8对
6.如图,直线AB与CD相交于点E,∠CEB=50°,EF⊥AE,则∠DEF的度数为( )
A.130° B.140° C.150° D.160°
7.给出下列说法:
(1)两条直线被第三条直线所截,同位角相等;
(2)不相等的两个角不是同位角;
(3)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;
(4)从直线外一点到这条直线的垂线段的长度,叫做该点到直线的距离;
其中正确的说法有( )
A.0个 B.1个 C.2个 D.3个
8.如图所示,同位角共有( )
A.6对 B.8对 C.10对 D.12对
9.下列说法正确的是( )
A.若两条直线被第三条直线所截,则同旁内角互补
B.相等的角是对顶角
C.有一条公共边并且和为180°的两个角互为邻补角
D.若三条直线两两相交,则共有6对对顶角
10.如图,∠ABD的同旁内角共有( )
A.1个 B.2个 C.3个 D.4个
二.填空题
11.如图,下列结论:①∠2与∠3是内错角;②∠2与∠B是同位角;③∠A与∠B是同旁内角;④∠A与∠ACB不是同旁内角,其中正确的是 (只填序号).
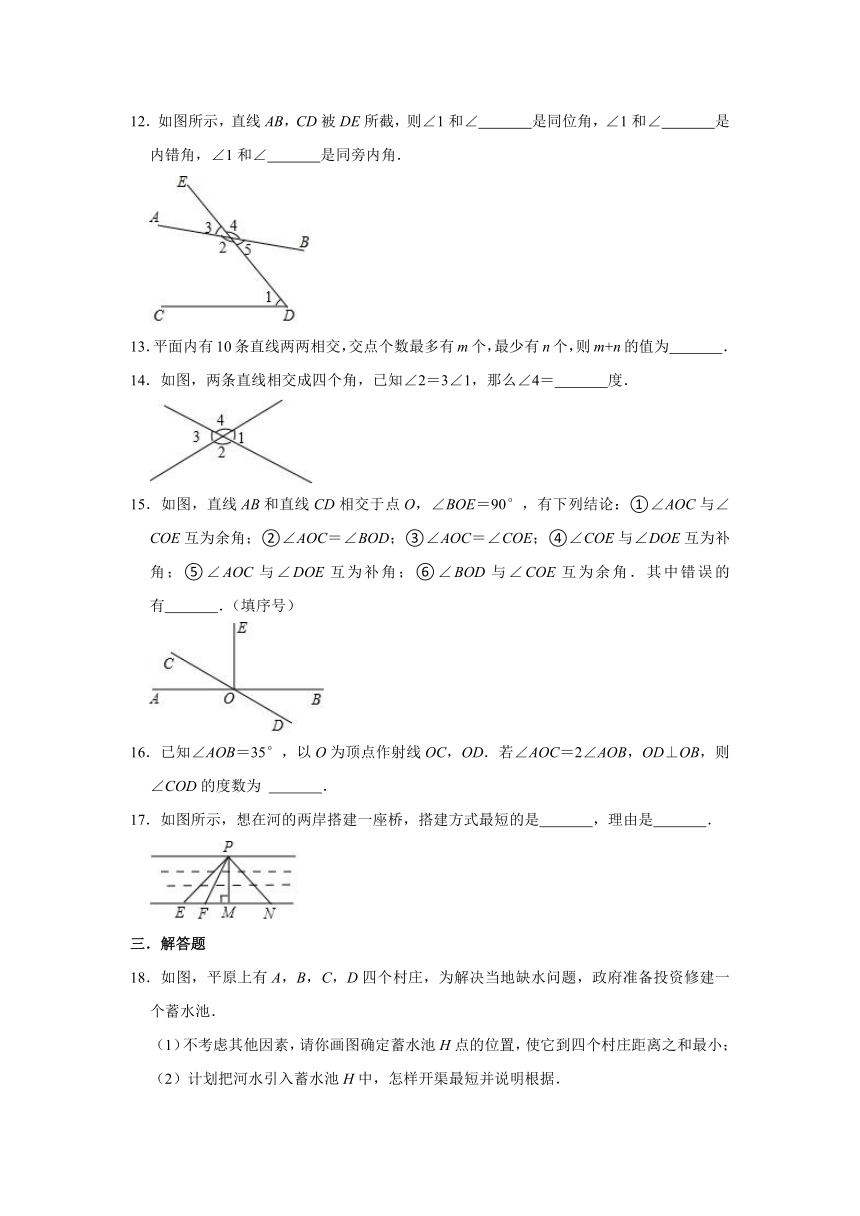
12.如图所示,直线AB,CD被DE所截,则∠1和∠ 是同位角,∠1和∠ 是内错角,∠1和∠ 是同旁内角.
13.平面内有10条直线两两相交,交点个数最多有m个,最少有n个,则m+n的值为 .
14.如图,两条直线相交成四个角,已知∠2=3∠1,那么∠4= 度.
15.如图,直线AB和直线CD相交于点O,∠BOE=90°,有下列结论:①∠AOC与∠COE互为余角;②∠AOC=∠BOD;③∠AOC=∠COE;④∠COE与∠DOE互为补角;⑤∠AOC与∠DOE互为补角;⑥∠BOD与∠COE互为余角.其中错误的有 .(填序号)
16.已知∠AOB=35°,以O为顶点作射线OC,OD.若∠AOC=2∠AOB,OD⊥OB,则∠COD的度数为 .
17.如图所示,想在河的两岸搭建一座桥,搭建方式最短的是 ,理由是 .
三.解答题
18.如图,平原上有A,B,C,D四个村庄,为解决当地缺水问题,政府准备投资修建一个蓄水池.
(1)不考虑其他因素,请你画图确定蓄水池H点的位置,使它到四个村庄距离之和最小;
(2)计划把河水引入蓄水池H中,怎样开渠最短并说明根据.
19.如图,P是∠AOB的边OB上一点.
(1)过点P画OA的垂线,垂足为H;
(2)过点P画OB的垂线,交OA于点C;
(3)点O到直线PC的距离是线段 的长度;
(4)比较PH与CO的大小,并说明理由.
20.如图,在△ABC中,∠ABC=90,过点B作三角形ABC的AC边上的高BD,过D点作三角形ABD的AB边上的高DE.
∠A的同位角是 .
∠ABD的内错角是 .
点B到直线AC的距离是线段 的长度.
点D到直线AB的距离是线段 的长度.
21.如图,AB、CD相交于点O,OM平分∠BOD,∠MON是直角,∠AOC=50°.
(1)求∠AON的度数;
(2)求∠DON的邻补角的度数.
22.已知如图,直线AB、CD相交于点O,∠COE=90°.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数;
(3)在(2)的条件下,过点O作OF⊥AB,请直接写出∠EOF的度数.
23.如图,直线CD与EF相交于点O,∠COE=60°,将一直角三角尺AOB的直角顶点与O重合,OA平分∠COE.
(1)求∠BOD的度数;
(2)将三角尺AOB以每秒3°的速度绕点O顺时针旋转,同时直线EF也以每秒9°的速度绕点O顺时针旋转,设运动时间为t秒(0≤t≤40).
①当t为何值时,直线EF平分∠AOB;
②若直线EF平分∠BOD,直接写出t的值.
参考答案
一.选择题
1.解:如图所示:
∴则a的可能取值有0,1,3,4,5,6,共6个.
故选:D.
2.解:根据题意可得:8条直线相交于一点时交点最少,此时交点为1个,即m=1;
任意两直线相交都产生一个交点时交点最多,
∵任意三条直线不过同一点,
∴此时交点为:8×(8﹣1)÷2=28,即n=28;
则m+n=29.
故选:C.
3.解:①两点确定一条直线,那么过两点有且只有一条直线,故①正确.
②根据两点间的距离的定义,连接两点的线段的长度叫做两点的距离,故②不正确.
③根据平角定义,平角具有共同顶点且两边在一条直线上,故③不正确.
④根据角平分线的定义,角平分线是从这个角的顶点出发并将这个分成两个相等的角的一条射线,那么若∠AOC=2∠BOC,则OB不一定是∠AOC的平分线,故④不正确.
⑤三条直线两两相交,有3个或1个交点,故⑤不正确.
综上:正确的有①,共1个.
故选:A.
4.解:图中对顶角有:∠AOF与∠BOE、∠AOD与∠BOC、∠FOD与∠EOC、∠FOB与∠AOE、∠DOB与∠AOC、∠DOE与∠COF,共6对.
故选:D.
5.解:如图,邻补角有:∠AOC与∠AOD,∠AOD与∠BOD,∠BOD与∠BOC,∠BOE与∠AOE,∠BOC与∠AOC,∠COE与∠DOE.
所以共6对.
故选:B.
6.解:∵∠CEB=50°,
∴∠AED=50°,
∵EF⊥AE,
∴∠DEF=∠AED+∠AEF=50°+90°=140°,
故选:B.
7.解:(1)两条平行的直线被第三条直线所截,同位角才相等,故(1)不正确.
(2)若两条直线被第三条直线所截,在截线的同一侧且在被截线的同一方向的两个角是同位角.两直线平行,同位角相等.不平行的两条直线被第三条直线所截,则同位角不相等.那么,(2)不正确.
(3)当平面内的一条直线l和两条平行线AB与CD中的一条AB相交,若l与CD不相交,则l∥CD,故推断出l∥AB,即l与AB不相交与题干矛盾.那么,l与CD也相较,故(3)正确.
(4)根据点到直线的距离定义,可知(4)正确.
∴正确的说法有2个.
故选:C.
8.解:如图,由AB、CD、EF组成的“三线八角”中同位角有四对,
射线GM和直线CD被直线EF所截,形成2对同位角;
射线GM和直线HN被直线EF所截,形成2对同位角;
射线HN和直线AB被直线EF所截,形成2对同位角.
则总共10对.
故选:C.
9.解:A、应该是“若两条平行直线被第三条直线所截,则同旁内角互补”,故错误;
B、相等的角不一定都是对顶角,如两直线平行,其中的同位角相等但不是对顶角,故错误;
C、如果这两个角在公共边的同侧,则不是邻补角,故错误;
D、正确.
故选:D.
10.解:∠ABD与∠ADB是直线AB、AD,被直线BD所截而成的同旁内角,
∠ABD与∠AEB是直线AB、AC,被直线BD所截而成的同旁内角,
∠ABD与∠BAE是直线AC、BD,被直线AB所截而成的同旁内角,
∠ABD与∠BAD是直线AD、BD,被直线AB所截而成的同旁内角,
故选:D.
二.填空题
11.解:∠2与∠3是直线AB、直线BC,被直线CD所截的一对内错角,因此①符合题意;
∠2与∠B是直线CD、直线BC,被直线AB所截的一对同位角,因此②符合题意;
∠A与∠B是直线AC、直线BC,被直线AB所截的一对同旁内角,因此③符合题意,
∠A与∠ACB是直线AB、直线BC,被直线AC所截的一对同旁内角,因此④不符合题意,
故答案为:①②③.
12.解:如图所示,直线AB,CD被DE所截,则∠1和∠3是同位角,∠1和∠5是内错角,∠1和∠2是同旁内角,
故答案为:3,5,2
13.解:根据题意可得:10条直线相交于一点时交点最少,此时交点为1个,
即n=1;
任意两直线相交都产生一个交点时,交点最多,
∴此时交点为:10×(10﹣1)÷2=45,
即m=45;
则m+n=45+1=46.
故答案为:46.
14.解:∵∠2=3∠1,∠1+∠2=180°,
∴∠2=135°,
则∠4=∠2=135°,
故答案为:135
15.解:∵∠BOE=90°,
∴∠AOE=180°﹣∠BOE=180°﹣90°=90°=∠AOC+∠COE,
因此①不符合题意;
由对顶角相等可得②不符合题意;
∵∠AOE=90°=∠AOC+∠COE,但∠AOC与∠COE不一定相等,因此③符合题意;
∠COE+∠DOE=180°,因此④不符合题意;
∠EOC+∠DOE=180°,但∠AOC与∠COE不一定相等,因此⑤符合题意;
∠BOD=∠AOC,且∠COE+∠AOC=90°,因此⑥不符合题意;
故答案为:③⑤
16.解:(1)OC、OD在直线OB同侧,
当OC、OD在直线OB上方时,如图,
∵∠AOB=35°,
∴∠AOC=2∠AOB=70°,
∴∠BOC=35°+70°=105°,
∵OD⊥OB,
∴∠BOD=90°,
∴∠COD=105°﹣90°=15°.
当OC、OD在直线OB下方时,如图,
∵∠AOB=35°,
∴∠BOC=∠AOB=35°,
∵OD⊥OB,
∴∠BOD=90°,
∴∠COD=90°﹣35°=55°.
(2)OC、OD在直线OB同侧,
当OC在直线OB上方、OD在直线OB下方时,如图,
∵∠AOB=35°,
∴∠AOC=2∠AOB=70°,
∵OD⊥OB,
∴∠BOD=90°,
∴∠COD=360°﹣90°﹣70°﹣35°=165°.
当OC在直线OB下方、OD在直线OB上方时,如图,
∵∠AOB=35°,
∴∠BOC=∠AOB=35°,
∵OD⊥OB,
∴∠BOD=90°,
∴∠COD=90°+35°=125°.
故答案为:15°,55°,125°,165°.
17.解:
∵PM⊥MN,
∴由垂线段最短可知PM是最短的,
故答案为:PM,垂线段最短.
三.解答题
18.解:(1)∵两点之间线段最短,
∴连接AD,BC交于H,则H为蓄水池位置,它到四个村庄距离之和最小.
(2)过H作HG⊥EF,垂足为G.
“过直线外一点与直线上各点的连线中,垂线段最短”是把河水引入蓄水池H中开渠最短的根据.
19.解:(1)作图,
(2)作图,
(3)OP,
故答案为:OP;
(4)PH<CO,
∵垂线段最短,
∴PH<PO,PO<OC,
∴PH<CO.
20.解:∠A的同位角是∠BDC、∠BED、∠EDC,
∠ABD的内错角是∠BDC,
点B到直线AC的距离是线段 BD的长度,
点D到直线AB的距离是线段 DE的长度,
故答案为:∠BDC、∠BED,BD,DE.
21.解:(1)∵OM平分∠BOD,∠BOD=∠AOC=50°,
∴∠BOM=∠DOM=25°,
又由∠MON=90°,
∴∠AON=180°﹣(∠MON+∠BOM)=180°﹣(90°+25°)=65°;
(2)∵∠AON=65°,∠AOC=50°,
∴∠CON=∠AON+∠AOC=115°,即∠DON的邻补角的度数为115°.
22.解:(1)∵∠AOC=36°,∠COE=90°,
∴∠BOE=180°﹣∠AOC﹣∠COE=54°;
(2)∵∠BOD:∠BOC=1:5,
∴∠BOD=180°×=30°,
∴∠AOC=30°,
∴∠AOE=30°+90°=120°;
(3)如图1,∠EOF=120°﹣90°=30°,
或如图2,∠EOF=360°﹣120°﹣90°=150°.
故∠EOF的度数是30°或150°.
23.解:(1)∵∠COE=60°,OA平分∠COE,
∴∠AOC=30°,
又∵∠AOB=90°,
∴∠BOD=180°﹣30°﹣90°=60°;
(2)①分两种情况:
①当OE平分∠AOB时,∠AOE=45°,
即9°t+30°﹣3°t=45°,
解得t=2.5;
②当OF平分∠AOB时,∠AOF=45°,
即9°t﹣150°﹣3°t=45°,
解得t=32.5;
综上所述,当t=2.5s或32.5s时,直线EF平分∠AOB;
②t的值为12s或36s.
分两种情况:
①当OE平分∠BOD时,∠BOE=∠BOD,
即9°t﹣60°﹣3°t=(60°﹣3°t),
解得t=12;
②当OF平分∠BOD时,∠DOF=∠BOD,
即9°t﹣300°=(3°t﹣60°),
解得t=36;
综上所述,若直线EF平分∠BOD,t的值为12s或36s.
一.选择题
1.若四条直线在平面内交点的个数为a,则a的可能取值有( )
A.3个 B.4个 C.5个 D.6个
2.平面内两两相交的8条直线,其交点个数最少为m个,最多为n个,则m+n等于( )
A.16 B.18 C.29 D.28
3.下列说法中正确的有( )
①过两点有且只有一条直线;
②连接两点的线段叫做两点的距离;
③平角是一条直线;
④若∠AOC=2∠BOC,则OB是∠AOC的平分线;
⑤三条直线两两相交,只有1个交点.
A.1个 B.2个 C.3个 D.4个
4.如图,直线AB、CD、EF相交于O,图中对顶角共有( )
A.3对 B.4对 C.5对 D.6对
5.如图,直线AB、CD相交于点O,作射线OE,则图中邻补角有( )
A.4对 B.6对 C.7对 D.8对
6.如图,直线AB与CD相交于点E,∠CEB=50°,EF⊥AE,则∠DEF的度数为( )
A.130° B.140° C.150° D.160°
7.给出下列说法:
(1)两条直线被第三条直线所截,同位角相等;
(2)不相等的两个角不是同位角;
(3)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;
(4)从直线外一点到这条直线的垂线段的长度,叫做该点到直线的距离;
其中正确的说法有( )
A.0个 B.1个 C.2个 D.3个
8.如图所示,同位角共有( )
A.6对 B.8对 C.10对 D.12对
9.下列说法正确的是( )
A.若两条直线被第三条直线所截,则同旁内角互补
B.相等的角是对顶角
C.有一条公共边并且和为180°的两个角互为邻补角
D.若三条直线两两相交,则共有6对对顶角
10.如图,∠ABD的同旁内角共有( )
A.1个 B.2个 C.3个 D.4个
二.填空题
11.如图,下列结论:①∠2与∠3是内错角;②∠2与∠B是同位角;③∠A与∠B是同旁内角;④∠A与∠ACB不是同旁内角,其中正确的是 (只填序号).
12.如图所示,直线AB,CD被DE所截,则∠1和∠ 是同位角,∠1和∠ 是内错角,∠1和∠ 是同旁内角.
13.平面内有10条直线两两相交,交点个数最多有m个,最少有n个,则m+n的值为 .
14.如图,两条直线相交成四个角,已知∠2=3∠1,那么∠4= 度.
15.如图,直线AB和直线CD相交于点O,∠BOE=90°,有下列结论:①∠AOC与∠COE互为余角;②∠AOC=∠BOD;③∠AOC=∠COE;④∠COE与∠DOE互为补角;⑤∠AOC与∠DOE互为补角;⑥∠BOD与∠COE互为余角.其中错误的有 .(填序号)
16.已知∠AOB=35°,以O为顶点作射线OC,OD.若∠AOC=2∠AOB,OD⊥OB,则∠COD的度数为 .
17.如图所示,想在河的两岸搭建一座桥,搭建方式最短的是 ,理由是 .
三.解答题
18.如图,平原上有A,B,C,D四个村庄,为解决当地缺水问题,政府准备投资修建一个蓄水池.
(1)不考虑其他因素,请你画图确定蓄水池H点的位置,使它到四个村庄距离之和最小;
(2)计划把河水引入蓄水池H中,怎样开渠最短并说明根据.
19.如图,P是∠AOB的边OB上一点.
(1)过点P画OA的垂线,垂足为H;
(2)过点P画OB的垂线,交OA于点C;
(3)点O到直线PC的距离是线段 的长度;
(4)比较PH与CO的大小,并说明理由.
20.如图,在△ABC中,∠ABC=90,过点B作三角形ABC的AC边上的高BD,过D点作三角形ABD的AB边上的高DE.
∠A的同位角是 .
∠ABD的内错角是 .
点B到直线AC的距离是线段 的长度.
点D到直线AB的距离是线段 的长度.
21.如图,AB、CD相交于点O,OM平分∠BOD,∠MON是直角,∠AOC=50°.
(1)求∠AON的度数;
(2)求∠DON的邻补角的度数.
22.已知如图,直线AB、CD相交于点O,∠COE=90°.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数;
(3)在(2)的条件下,过点O作OF⊥AB,请直接写出∠EOF的度数.
23.如图,直线CD与EF相交于点O,∠COE=60°,将一直角三角尺AOB的直角顶点与O重合,OA平分∠COE.
(1)求∠BOD的度数;
(2)将三角尺AOB以每秒3°的速度绕点O顺时针旋转,同时直线EF也以每秒9°的速度绕点O顺时针旋转,设运动时间为t秒(0≤t≤40).
①当t为何值时,直线EF平分∠AOB;
②若直线EF平分∠BOD,直接写出t的值.
参考答案
一.选择题
1.解:如图所示:
∴则a的可能取值有0,1,3,4,5,6,共6个.
故选:D.
2.解:根据题意可得:8条直线相交于一点时交点最少,此时交点为1个,即m=1;
任意两直线相交都产生一个交点时交点最多,
∵任意三条直线不过同一点,
∴此时交点为:8×(8﹣1)÷2=28,即n=28;
则m+n=29.
故选:C.
3.解:①两点确定一条直线,那么过两点有且只有一条直线,故①正确.
②根据两点间的距离的定义,连接两点的线段的长度叫做两点的距离,故②不正确.
③根据平角定义,平角具有共同顶点且两边在一条直线上,故③不正确.
④根据角平分线的定义,角平分线是从这个角的顶点出发并将这个分成两个相等的角的一条射线,那么若∠AOC=2∠BOC,则OB不一定是∠AOC的平分线,故④不正确.
⑤三条直线两两相交,有3个或1个交点,故⑤不正确.
综上:正确的有①,共1个.
故选:A.
4.解:图中对顶角有:∠AOF与∠BOE、∠AOD与∠BOC、∠FOD与∠EOC、∠FOB与∠AOE、∠DOB与∠AOC、∠DOE与∠COF,共6对.
故选:D.
5.解:如图,邻补角有:∠AOC与∠AOD,∠AOD与∠BOD,∠BOD与∠BOC,∠BOE与∠AOE,∠BOC与∠AOC,∠COE与∠DOE.
所以共6对.
故选:B.
6.解:∵∠CEB=50°,
∴∠AED=50°,
∵EF⊥AE,
∴∠DEF=∠AED+∠AEF=50°+90°=140°,
故选:B.
7.解:(1)两条平行的直线被第三条直线所截,同位角才相等,故(1)不正确.
(2)若两条直线被第三条直线所截,在截线的同一侧且在被截线的同一方向的两个角是同位角.两直线平行,同位角相等.不平行的两条直线被第三条直线所截,则同位角不相等.那么,(2)不正确.
(3)当平面内的一条直线l和两条平行线AB与CD中的一条AB相交,若l与CD不相交,则l∥CD,故推断出l∥AB,即l与AB不相交与题干矛盾.那么,l与CD也相较,故(3)正确.
(4)根据点到直线的距离定义,可知(4)正确.
∴正确的说法有2个.
故选:C.
8.解:如图,由AB、CD、EF组成的“三线八角”中同位角有四对,
射线GM和直线CD被直线EF所截,形成2对同位角;
射线GM和直线HN被直线EF所截,形成2对同位角;
射线HN和直线AB被直线EF所截,形成2对同位角.
则总共10对.
故选:C.
9.解:A、应该是“若两条平行直线被第三条直线所截,则同旁内角互补”,故错误;
B、相等的角不一定都是对顶角,如两直线平行,其中的同位角相等但不是对顶角,故错误;
C、如果这两个角在公共边的同侧,则不是邻补角,故错误;
D、正确.
故选:D.
10.解:∠ABD与∠ADB是直线AB、AD,被直线BD所截而成的同旁内角,
∠ABD与∠AEB是直线AB、AC,被直线BD所截而成的同旁内角,
∠ABD与∠BAE是直线AC、BD,被直线AB所截而成的同旁内角,
∠ABD与∠BAD是直线AD、BD,被直线AB所截而成的同旁内角,
故选:D.
二.填空题
11.解:∠2与∠3是直线AB、直线BC,被直线CD所截的一对内错角,因此①符合题意;
∠2与∠B是直线CD、直线BC,被直线AB所截的一对同位角,因此②符合题意;
∠A与∠B是直线AC、直线BC,被直线AB所截的一对同旁内角,因此③符合题意,
∠A与∠ACB是直线AB、直线BC,被直线AC所截的一对同旁内角,因此④不符合题意,
故答案为:①②③.
12.解:如图所示,直线AB,CD被DE所截,则∠1和∠3是同位角,∠1和∠5是内错角,∠1和∠2是同旁内角,
故答案为:3,5,2
13.解:根据题意可得:10条直线相交于一点时交点最少,此时交点为1个,
即n=1;
任意两直线相交都产生一个交点时,交点最多,
∴此时交点为:10×(10﹣1)÷2=45,
即m=45;
则m+n=45+1=46.
故答案为:46.
14.解:∵∠2=3∠1,∠1+∠2=180°,
∴∠2=135°,
则∠4=∠2=135°,
故答案为:135
15.解:∵∠BOE=90°,
∴∠AOE=180°﹣∠BOE=180°﹣90°=90°=∠AOC+∠COE,
因此①不符合题意;
由对顶角相等可得②不符合题意;
∵∠AOE=90°=∠AOC+∠COE,但∠AOC与∠COE不一定相等,因此③符合题意;
∠COE+∠DOE=180°,因此④不符合题意;
∠EOC+∠DOE=180°,但∠AOC与∠COE不一定相等,因此⑤符合题意;
∠BOD=∠AOC,且∠COE+∠AOC=90°,因此⑥不符合题意;
故答案为:③⑤
16.解:(1)OC、OD在直线OB同侧,
当OC、OD在直线OB上方时,如图,
∵∠AOB=35°,
∴∠AOC=2∠AOB=70°,
∴∠BOC=35°+70°=105°,
∵OD⊥OB,
∴∠BOD=90°,
∴∠COD=105°﹣90°=15°.
当OC、OD在直线OB下方时,如图,
∵∠AOB=35°,
∴∠BOC=∠AOB=35°,
∵OD⊥OB,
∴∠BOD=90°,
∴∠COD=90°﹣35°=55°.
(2)OC、OD在直线OB同侧,
当OC在直线OB上方、OD在直线OB下方时,如图,
∵∠AOB=35°,
∴∠AOC=2∠AOB=70°,
∵OD⊥OB,
∴∠BOD=90°,
∴∠COD=360°﹣90°﹣70°﹣35°=165°.
当OC在直线OB下方、OD在直线OB上方时,如图,
∵∠AOB=35°,
∴∠BOC=∠AOB=35°,
∵OD⊥OB,
∴∠BOD=90°,
∴∠COD=90°+35°=125°.
故答案为:15°,55°,125°,165°.
17.解:
∵PM⊥MN,
∴由垂线段最短可知PM是最短的,
故答案为:PM,垂线段最短.
三.解答题
18.解:(1)∵两点之间线段最短,
∴连接AD,BC交于H,则H为蓄水池位置,它到四个村庄距离之和最小.
(2)过H作HG⊥EF,垂足为G.
“过直线外一点与直线上各点的连线中,垂线段最短”是把河水引入蓄水池H中开渠最短的根据.
19.解:(1)作图,
(2)作图,
(3)OP,
故答案为:OP;
(4)PH<CO,
∵垂线段最短,
∴PH<PO,PO<OC,
∴PH<CO.
20.解:∠A的同位角是∠BDC、∠BED、∠EDC,
∠ABD的内错角是∠BDC,
点B到直线AC的距离是线段 BD的长度,
点D到直线AB的距离是线段 DE的长度,
故答案为:∠BDC、∠BED,BD,DE.
21.解:(1)∵OM平分∠BOD,∠BOD=∠AOC=50°,
∴∠BOM=∠DOM=25°,
又由∠MON=90°,
∴∠AON=180°﹣(∠MON+∠BOM)=180°﹣(90°+25°)=65°;
(2)∵∠AON=65°,∠AOC=50°,
∴∠CON=∠AON+∠AOC=115°,即∠DON的邻补角的度数为115°.
22.解:(1)∵∠AOC=36°,∠COE=90°,
∴∠BOE=180°﹣∠AOC﹣∠COE=54°;
(2)∵∠BOD:∠BOC=1:5,
∴∠BOD=180°×=30°,
∴∠AOC=30°,
∴∠AOE=30°+90°=120°;
(3)如图1,∠EOF=120°﹣90°=30°,
或如图2,∠EOF=360°﹣120°﹣90°=150°.
故∠EOF的度数是30°或150°.
23.解:(1)∵∠COE=60°,OA平分∠COE,
∴∠AOC=30°,
又∵∠AOB=90°,
∴∠BOD=180°﹣30°﹣90°=60°;
(2)①分两种情况:
①当OE平分∠AOB时,∠AOE=45°,
即9°t+30°﹣3°t=45°,
解得t=2.5;
②当OF平分∠AOB时,∠AOF=45°,
即9°t﹣150°﹣3°t=45°,
解得t=32.5;
综上所述,当t=2.5s或32.5s时,直线EF平分∠AOB;
②t的值为12s或36s.
分两种情况:
①当OE平分∠BOD时,∠BOE=∠BOD,
即9°t﹣60°﹣3°t=(60°﹣3°t),
解得t=12;
②当OF平分∠BOD时,∠DOF=∠BOD,
即9°t﹣300°=(3°t﹣60°),
解得t=36;
综上所述,若直线EF平分∠BOD,t的值为12s或36s.
