初中数学人教版八年级下册20.2数据的波动程度作业(含简单答案)
文档属性
| 名称 | 初中数学人教版八年级下册20.2数据的波动程度作业(含简单答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 740.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-20 00:00:00 | ||
图片预览



文档简介
初中数学数据的波动程度作业
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.甲、乙、丙、丁四人进行10次射击测试,他们的平均数相同,方差分别是,,,,则这四人中成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
2.为了学生的身心健康,提高学生就餐满意度,某学校对全体学生开展了食堂满意度问卷调查,满意度以分数呈现,从低到高为1分,2分,3分,4分,5分共五档,调查人员随机抽取了40份调查问卷,将数据整理成如图统计图.下列说法错误的是( )
平均数是分 B.众数是16分
C.中位数是分 D.极差为4
3.已知一组数据4,5,6,7,a的平均数为5,则这组数据的方差为( )
A.1 B. C. D.2
4.下表记录了甲、乙、丙、丁四名跳远运动员几次选拔赛成绩的平均数与方差.根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
甲 乙 丙 丁
平均数
方差
A.甲 B.乙 C.丙 D.丁
5.科学家同时培育了甲乙丙丁四种花,从甲乙丙丁选个开花时间最短的并且最平稳的.
种类 甲种类 乙种类 丙种类 丁种类
平均数 2.3 2.3 2.8 3.1
方差 1.05 0.78 1.05 0.78
A.甲种类 B.乙种类 C.丙种类 D.丁种类
6.“爱护环境,人人有责”.为减少塑料垃圾袋的使用,小明统计了他家某一周每天使用塑料垃圾袋的数量(单位:个):2,2,3,3,3,4,4.则对这组数据说法错误的是( )
A.众数是3 B.中位数是3 C.平均数是3 D.方差是3
7.蛟蛟同学在计算出6个数的平均数后,不小心将这个数也混到数据中了,那么重新计算这些新数据后一定不变的量是( )
A.平均数 B.中位数 C.众数 D.方差
8.为贯彻落实教育部办公厅关于“保障学生每天校内、校外各1小时体育活动时间”的要求,学校要求学生每天坚持体育锻炼.小亮记录了自己一周内每天校外锻炼的时间(单位:分钟),并制作了如图所示的统计图.
根据统计图,下列关于小亮该周每天校外锻炼时间的描述,正确的是( )
平均数为70分钟 B.众数为67分钟
C.中位数为67分钟 D.方差为0
9.某小组在一次“在线测试”中做对的题数分别是,对于这组数据,下列判断错误的是( )
A.众数是 B.中位数是 C.平均数是 D.方差是
10.A,B两名射击运动员进行了相同次数的射击,下列关于他们射击成绩的平均数和方差的描述中,能说明A成绩较好且更稳定的是( )
A.且. B.且.
C.且 D.且.
二、填空题
11.小颖参加“歌唱祖国”歌咏比赛,六位评委对小颖的打分(单位:分)如下:7,8,7,9,8,.这六个分数的极差是 分.
12.在甲、乙两位射击运动员的10次考核成绩中,两人的考核成绩的平均数相同, 方差分别为,,则考核成绩更为稳定的运动员是 (填“甲”、“乙”中的一个)
13.生物学研究表明,植物光合作用速率越高,单位时间内合成的有机物越多,为了解甲、乙两个品种大豆的光合作用速率,科研人员从甲、乙两个品种的大豆中各选五株,在同等实验条件下,测量它们的光合作用速率(单位:),结果统计如下:
品种 第一株 第二株 第三株 第四株 第五株 平均数
甲 32 30 25 18 20 25
乙 28 25 26 24 22 25
则两个大豆品种中光合作用速率更稳定的是 (填“甲”或“乙”).
14.某班进行了轮数学知识竞赛模拟赛,甲、乙、丙、丁名同学次模拟竞赛成绩的平均分分别是:甲分,乙分,丙分,丁分,方差分别是,,,,若要从这名同学中,选取一位同学参加学校比赛,选 最合适.
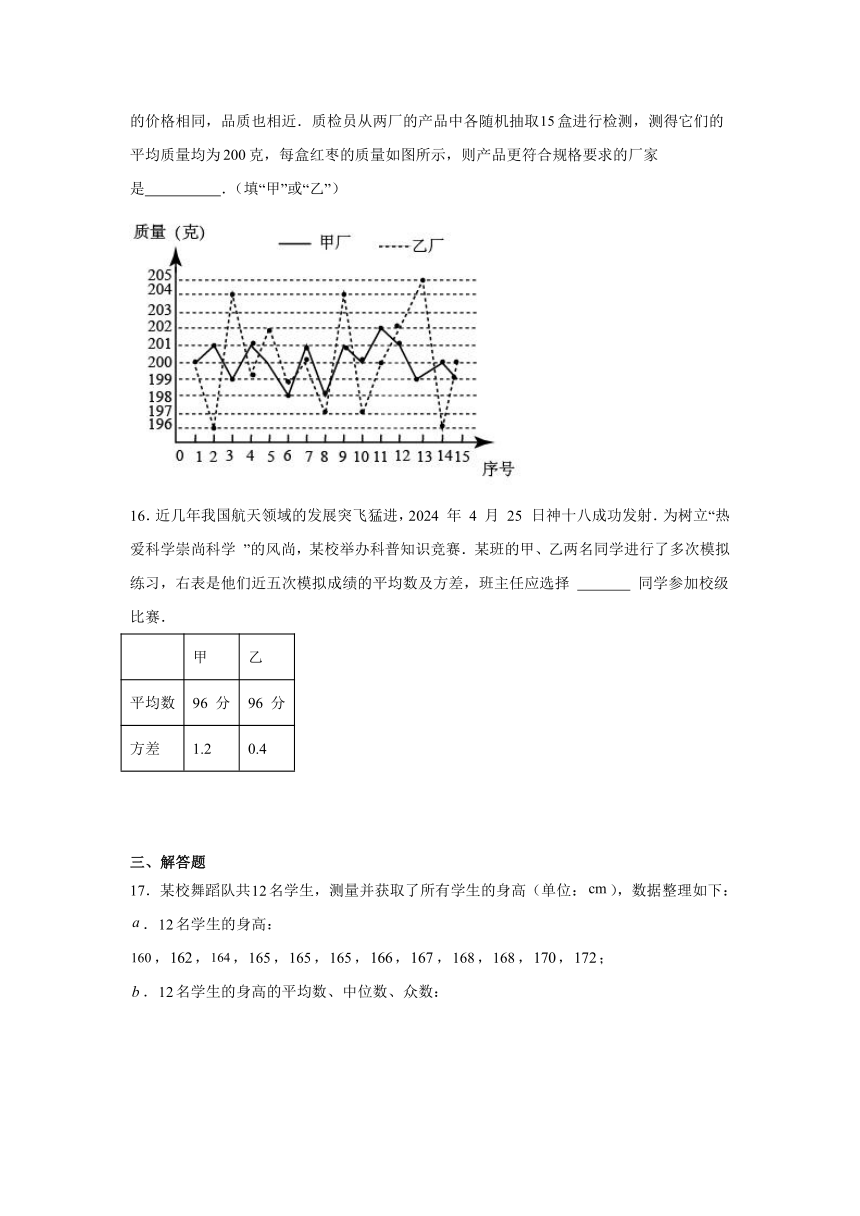
15.某外贸公司要出口一批规格为克/盒的红枣,现有甲、乙两个厂家提供货源,它们的价格相同,品质也相近.质检员从两厂的产品中各随机抽取盒进行检测,测得它们的平均质量均为克,每盒红枣的质量如图所示,则产品更符合规格要求的厂家是 .(填“甲”或“乙”)
16.近几年我国航天领域的发展突飞猛进,2024 年 4 月 25 日神十八成功发射.为树立“热 爱科学崇尚科学 ”的风尚,某校举办科普知识竞赛.某班的甲、乙两名同学进行了多次模拟练习,右表是他们近五次模拟成绩的平均数及方差,班主任应选择 同学参加校级比赛.
甲 乙
平均数 96 分 96 分
方差 1.2 0.4
三、解答题
17.某校舞蹈队共名学生,测量并获取了所有学生的身高(单位:),数据整理如下:
.名学生的身高:
,,,,,,,,,,,;
.名学生的身高的平均数、中位数、众数:
平均数 中位数 众数
表中 , ;
(2)对于不同组的学生,如果一组学生的身高的方差越小,则认为该组舞台呈现效果越好,据此推断:在下列两组学生中,舞台呈现效果更好的是 (填“甲组”或“乙组”);
甲组学生的身高
乙组学生的身高
(3)该舞蹈队要选五名学生参加比赛,已确定三名学生参赛,他们的身高分别为,,,他们的身高的方差为在选另外两名学生时,首先要求所选的两名学生与已确定的三名学生所组成的五名学生的身高的方差小于其次要求所选的两名学生与已确定的三名学生所组成的五名学生的身高的平均数尽可能大,则选出的另外两名学生的身高分别为 和 .
18.跳绳是一项有效的有氧运动,因其便捷特效被学校广泛选为促进学生体质健康的运动项目,某校八年级400名学生在“跳绳提升”训练前后各参加了一次规格相同的测试,测试成绩为整数,满分10分.
【收集整理数据】两次测试结果显示所有学生成绩都不低于6分,用抽样调查的方式从中抽取了50名学生训练前后的测试成绩.
【描述数据】根据抽取的学生成绩,绘制出了如下统计图.
【分析数据】抽取的样本数据的平均数、中位数、众数、方差如下表:
平均数 中位数 众数 方差
训练前 7.6 7 a 1.84
训练后 8.8 b 10 1.62
根据以上信息,解答下列问题:
(1) , ;
(2)补全条形统计图;
(3)估计八年级学生在训练后比训练前跳绳成绩满分的增加了多少人?
请从平均数、中位数、众数和方差这四个统计量中任意选一个,说明其在本题中的意义.
19.小红家到学校有两条公共汽车线路,为了解两条线路的乘车所用时间,小红做了试验,第一周(5个工作日)选择A线路,第二周(5个工作日)选择B线路,每天在固定时间段内乘车2次并分别记录所用时间,数据统计如下:(单位:min)
数据统计表
试验序号 1 2 3 4 5 6 7 8 9 10
A线路所用时间 15 32 15 16 34 18 21 14 35 20
B线路所用时间 25 29 23 25 27 26 31 28 30 24
数据折线统计图
根据以上信息解答下列问题:
平均数 中位数 众数 方差
A线路所用时间 22 a 15 63.2
B线路所用时间 b 26.5 c 6.36
(1)填空:__________;___________;___________;
(2)应用你所学的统计知识,帮助小红分析如何选择乘车线路.
20.蓬勃发展的快递业,为全国各地的新鲜水果及时走进千家万户提供了极大便利.不同的快递公司在配送、服务、收费和投递范围等方面各具优势.樱桃种植户小丽经过初步了解,打算从甲、乙两家快递公司中选择一家合作,为此,小丽收集了10家樱桃种植户对两家公司的相关评价,并整理、描述、分析如下:
a.配送速度得分(满分10分):
甲:6 6 7 7 7 8 9 9 9 10
乙:6 7 7 8 8 8 8 9 9 10
b.服务质量得分统计图(满分10分):
c.配送速度和服务质量得分统计表:
项目 统计量快递公司 配送速度得分 服务质量得分
平均数 中位数 平均数 方差
甲 7.8 m 7
乙 8 8 7
根据以上信息,回答下列问题:
(1)表格中的______;______(填“>”“=”或“<”).
(2)综合上表中的统计量,你认为小丽应选择哪家公司?请说明理由.
(3)为了从甲、乙两家公司中选出更合适的公司,你认为还应收集什么信息(列出一条即可)?
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.甲、乙、丙、丁四人进行10次射击测试,他们的平均数相同,方差分别是,,,,则这四人中成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
2.为了学生的身心健康,提高学生就餐满意度,某学校对全体学生开展了食堂满意度问卷调查,满意度以分数呈现,从低到高为1分,2分,3分,4分,5分共五档,调查人员随机抽取了40份调查问卷,将数据整理成如图统计图.下列说法错误的是( )
平均数是分 B.众数是16分
C.中位数是分 D.极差为4
3.已知一组数据4,5,6,7,a的平均数为5,则这组数据的方差为( )
A.1 B. C. D.2
4.下表记录了甲、乙、丙、丁四名跳远运动员几次选拔赛成绩的平均数与方差.根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
甲 乙 丙 丁
平均数
方差
A.甲 B.乙 C.丙 D.丁
5.科学家同时培育了甲乙丙丁四种花,从甲乙丙丁选个开花时间最短的并且最平稳的.
种类 甲种类 乙种类 丙种类 丁种类
平均数 2.3 2.3 2.8 3.1
方差 1.05 0.78 1.05 0.78
A.甲种类 B.乙种类 C.丙种类 D.丁种类
6.“爱护环境,人人有责”.为减少塑料垃圾袋的使用,小明统计了他家某一周每天使用塑料垃圾袋的数量(单位:个):2,2,3,3,3,4,4.则对这组数据说法错误的是( )
A.众数是3 B.中位数是3 C.平均数是3 D.方差是3
7.蛟蛟同学在计算出6个数的平均数后,不小心将这个数也混到数据中了,那么重新计算这些新数据后一定不变的量是( )
A.平均数 B.中位数 C.众数 D.方差
8.为贯彻落实教育部办公厅关于“保障学生每天校内、校外各1小时体育活动时间”的要求,学校要求学生每天坚持体育锻炼.小亮记录了自己一周内每天校外锻炼的时间(单位:分钟),并制作了如图所示的统计图.
根据统计图,下列关于小亮该周每天校外锻炼时间的描述,正确的是( )
平均数为70分钟 B.众数为67分钟
C.中位数为67分钟 D.方差为0
9.某小组在一次“在线测试”中做对的题数分别是,对于这组数据,下列判断错误的是( )
A.众数是 B.中位数是 C.平均数是 D.方差是
10.A,B两名射击运动员进行了相同次数的射击,下列关于他们射击成绩的平均数和方差的描述中,能说明A成绩较好且更稳定的是( )
A.且. B.且.
C.且 D.且.
二、填空题
11.小颖参加“歌唱祖国”歌咏比赛,六位评委对小颖的打分(单位:分)如下:7,8,7,9,8,.这六个分数的极差是 分.
12.在甲、乙两位射击运动员的10次考核成绩中,两人的考核成绩的平均数相同, 方差分别为,,则考核成绩更为稳定的运动员是 (填“甲”、“乙”中的一个)
13.生物学研究表明,植物光合作用速率越高,单位时间内合成的有机物越多,为了解甲、乙两个品种大豆的光合作用速率,科研人员从甲、乙两个品种的大豆中各选五株,在同等实验条件下,测量它们的光合作用速率(单位:),结果统计如下:
品种 第一株 第二株 第三株 第四株 第五株 平均数
甲 32 30 25 18 20 25
乙 28 25 26 24 22 25
则两个大豆品种中光合作用速率更稳定的是 (填“甲”或“乙”).
14.某班进行了轮数学知识竞赛模拟赛,甲、乙、丙、丁名同学次模拟竞赛成绩的平均分分别是:甲分,乙分,丙分,丁分,方差分别是,,,,若要从这名同学中,选取一位同学参加学校比赛,选 最合适.
15.某外贸公司要出口一批规格为克/盒的红枣,现有甲、乙两个厂家提供货源,它们的价格相同,品质也相近.质检员从两厂的产品中各随机抽取盒进行检测,测得它们的平均质量均为克,每盒红枣的质量如图所示,则产品更符合规格要求的厂家是 .(填“甲”或“乙”)
16.近几年我国航天领域的发展突飞猛进,2024 年 4 月 25 日神十八成功发射.为树立“热 爱科学崇尚科学 ”的风尚,某校举办科普知识竞赛.某班的甲、乙两名同学进行了多次模拟练习,右表是他们近五次模拟成绩的平均数及方差,班主任应选择 同学参加校级比赛.
甲 乙
平均数 96 分 96 分
方差 1.2 0.4
三、解答题
17.某校舞蹈队共名学生,测量并获取了所有学生的身高(单位:),数据整理如下:
.名学生的身高:
,,,,,,,,,,,;
.名学生的身高的平均数、中位数、众数:
平均数 中位数 众数
表中 , ;
(2)对于不同组的学生,如果一组学生的身高的方差越小,则认为该组舞台呈现效果越好,据此推断:在下列两组学生中,舞台呈现效果更好的是 (填“甲组”或“乙组”);
甲组学生的身高
乙组学生的身高
(3)该舞蹈队要选五名学生参加比赛,已确定三名学生参赛,他们的身高分别为,,,他们的身高的方差为在选另外两名学生时,首先要求所选的两名学生与已确定的三名学生所组成的五名学生的身高的方差小于其次要求所选的两名学生与已确定的三名学生所组成的五名学生的身高的平均数尽可能大,则选出的另外两名学生的身高分别为 和 .
18.跳绳是一项有效的有氧运动,因其便捷特效被学校广泛选为促进学生体质健康的运动项目,某校八年级400名学生在“跳绳提升”训练前后各参加了一次规格相同的测试,测试成绩为整数,满分10分.
【收集整理数据】两次测试结果显示所有学生成绩都不低于6分,用抽样调查的方式从中抽取了50名学生训练前后的测试成绩.
【描述数据】根据抽取的学生成绩,绘制出了如下统计图.
【分析数据】抽取的样本数据的平均数、中位数、众数、方差如下表:
平均数 中位数 众数 方差
训练前 7.6 7 a 1.84
训练后 8.8 b 10 1.62
根据以上信息,解答下列问题:
(1) , ;
(2)补全条形统计图;
(3)估计八年级学生在训练后比训练前跳绳成绩满分的增加了多少人?
请从平均数、中位数、众数和方差这四个统计量中任意选一个,说明其在本题中的意义.
19.小红家到学校有两条公共汽车线路,为了解两条线路的乘车所用时间,小红做了试验,第一周(5个工作日)选择A线路,第二周(5个工作日)选择B线路,每天在固定时间段内乘车2次并分别记录所用时间,数据统计如下:(单位:min)
数据统计表
试验序号 1 2 3 4 5 6 7 8 9 10
A线路所用时间 15 32 15 16 34 18 21 14 35 20
B线路所用时间 25 29 23 25 27 26 31 28 30 24
数据折线统计图
根据以上信息解答下列问题:
平均数 中位数 众数 方差
A线路所用时间 22 a 15 63.2
B线路所用时间 b 26.5 c 6.36
(1)填空:__________;___________;___________;
(2)应用你所学的统计知识,帮助小红分析如何选择乘车线路.
20.蓬勃发展的快递业,为全国各地的新鲜水果及时走进千家万户提供了极大便利.不同的快递公司在配送、服务、收费和投递范围等方面各具优势.樱桃种植户小丽经过初步了解,打算从甲、乙两家快递公司中选择一家合作,为此,小丽收集了10家樱桃种植户对两家公司的相关评价,并整理、描述、分析如下:
a.配送速度得分(满分10分):
甲:6 6 7 7 7 8 9 9 9 10
乙:6 7 7 8 8 8 8 9 9 10
b.服务质量得分统计图(满分10分):
c.配送速度和服务质量得分统计表:
项目 统计量快递公司 配送速度得分 服务质量得分
平均数 中位数 平均数 方差
甲 7.8 m 7
乙 8 8 7
根据以上信息,回答下列问题:
(1)表格中的______;______(填“>”“=”或“<”).
(2)综合上表中的统计量,你认为小丽应选择哪家公司?请说明理由.
(3)为了从甲、乙两家公司中选出更合适的公司,你认为还应收集什么信息(列出一条即可)?
