2024年中考数学复习 平行四边形存在性问题复习讲义(含答案)
文档属性
| 名称 | 2024年中考数学复习 平行四边形存在性问题复习讲义(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-20 10:02:54 | ||
图片预览


文档简介
平行四边形存在性问题复习讲义
解题策略
关于四边形为平行四边形的问题,要分以下几种情况进行讨论:
1.若三点坐标已知,则分别以三点所确定的线段为对角线,利用中点坐标公式进行解答;或者分别以三点所确定的线段为边,利用平行四边形对边平行且相等,利用平移进行解答.
2.若两点的坐标已知,第三点为已知直线(或曲线)上的动点,则用参数表示出第三点的坐标,然后借助对角线讨论法,利用中点坐标公式进行解答.
点 P(a,b)是点 A(xA,yA)与点. 的中点,也可以说点A、B关于点P 成中心对称,则 P 点的坐标为 即
如果四边形ABCD为平行四边形, 因为平行四边形的对角线互相平分,交点为对角线的中点,所以有 整理,得 或
模型一 三点定型
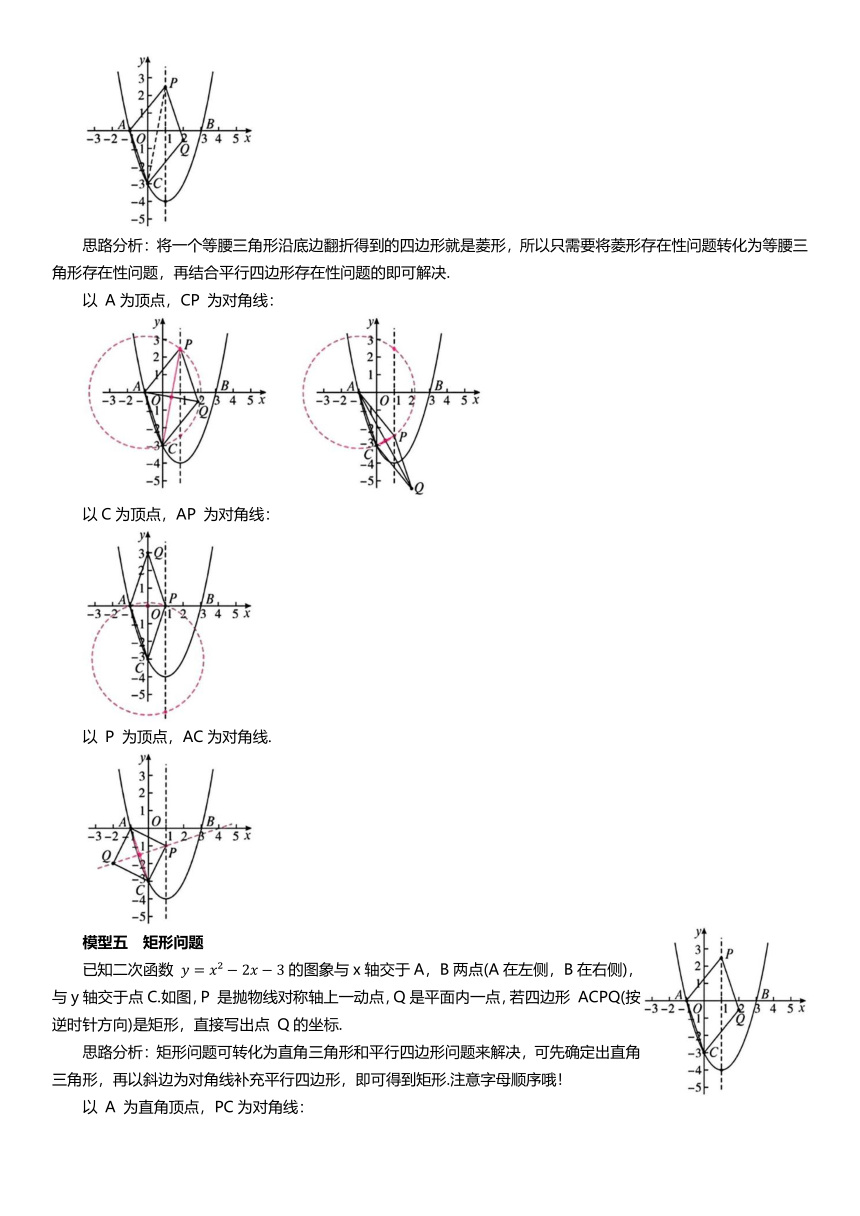
已知二次函数 的图象与x轴交于A,B 两点(A在左侧,B在右侧),与y轴交于C点,顶点为 D.
如图,M为平面内一点,若A,B,C,M为顶点的四边形是平行四边形,直接写出 M点坐标.
思路分析:平行四边形存在性问题,且是三点坐标已知,求第四个点的问题,只要采用对角线讨论法(分别以AB,BC,AC为对角线作平行四边形),即可做到不重、不漏.
模型二 两点定型
已知二次函数 的图象与x轴交于A,B两点(A在左侧,B在右侧),与 y轴交于C点,顶点为 D.
如图,M是x轴上一动点,N 是抛物线上一动点.若以A,C,M,N 为顶点的四边形是平行四边形,直接写出点 M的坐标.
思路分析:平行四边形存在性问题,且是A、C两点坐标已知,求其余两个点的问题,只要采用对角线讨论法(分别以AM,MC,AC为对角线作平行四边形),即可做到不重、不漏.
模型三 一点定型
已知二次函数 的图象与x轴交于A,B两点(A 在左侧,B 在右侧),与y轴交于C点,顶点为 D.
如图,抛物线对称轴与x轴交于点E,M是线段AB 上一动点,且 交抛物线对称轴于点N,P 是抛物线上一点.若以M,N,P,E为顶点的四边形是平行四边形,直接写出点 P 的坐标.
思路分析:平行四边形存在性问题,且是E点坐标已知,求其余三个动点中的一个点的坐标问题,只要采用对角线讨论法(分别以 EM,NE,MN为对角线作平行四边形),即可做到不重、不漏.
模型四 菱形问题
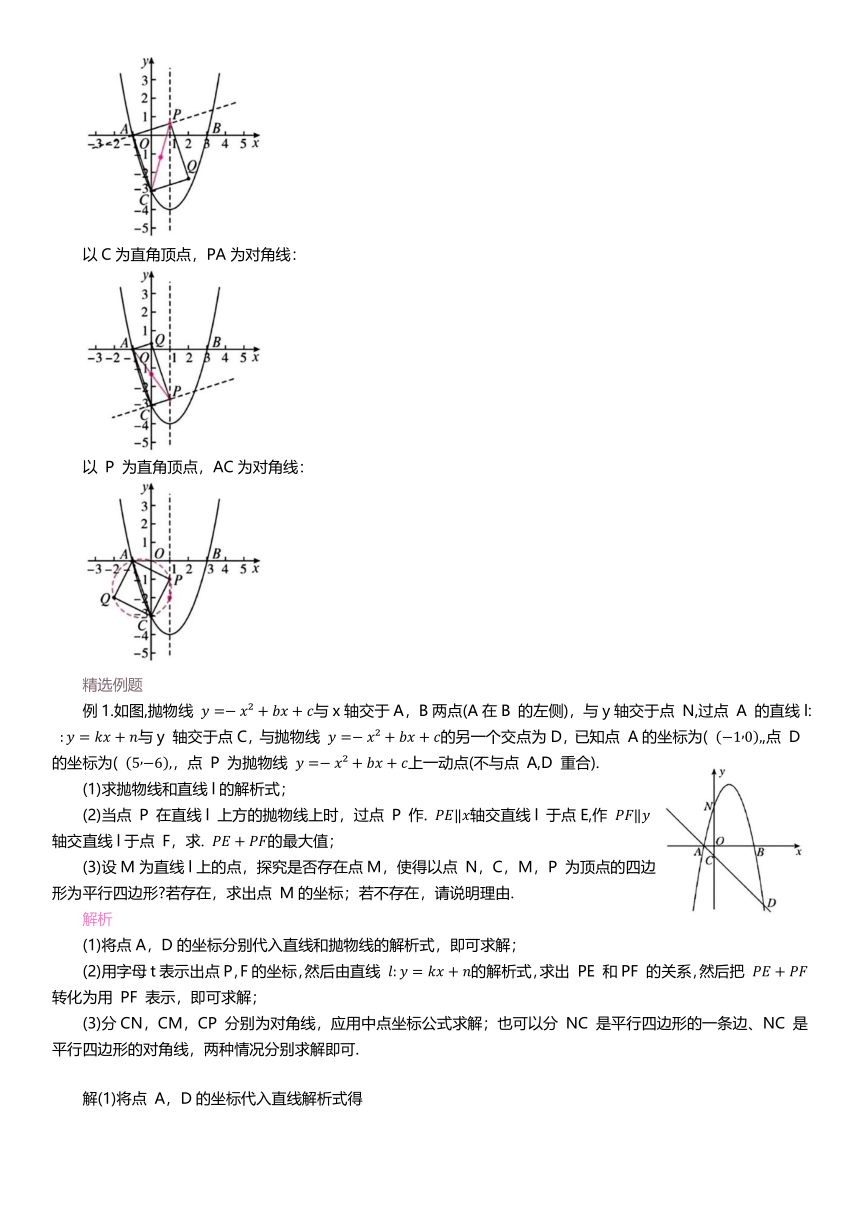
已知二次函数 的图象与x轴交于A,B两点(A在左侧,B在右侧),与y轴交于C点.如图,P 是抛物线对称轴上一动点,Q是坐标系内一点,若四边形 ACQP 是菱形,直接写出点 Q的坐标.
思路分析:将一个等腰三角形沿底边翻折得到的四边形就是菱形,所以只需要将菱形存在性问题转化为等腰三角形存在性问题,再结合平行四边形存在性问题的即可解决.
以 A为顶点,CP 为对角线:
以C为顶点,AP 为对角线:
以 P 为顶点,AC为对角线.
模型五 矩形问题
已知二次函数 的图象与x轴交于A,B两点(A在左侧,B在右侧),与y轴交于点C.如图,P 是抛物线对称轴上一动点,Q是平面内一点,若四边形 ACPQ(按逆时针方向)是矩形,直接写出点 Q的坐标.
思路分析:矩形问题可转化为直角三角形和平行四边形问题来解决,可先确定出直角三角形,再以斜边为对角线补充平行四边形,即可得到矩形.注意字母顺序哦!
以 A 为直角顶点,PC为对角线:
以C为直角顶点,PA为对角线:
以 P 为直角顶点,AC为对角线:
精选例题
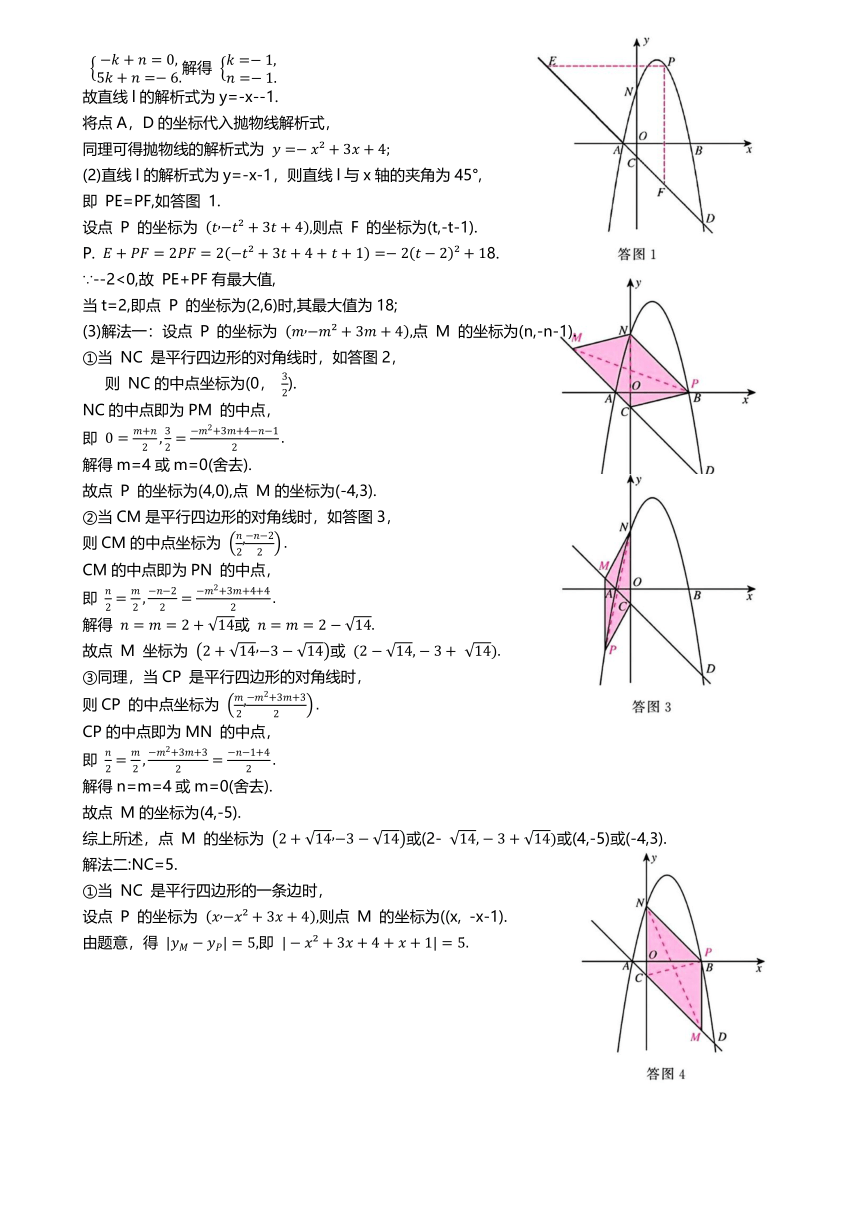
例1.如图,抛物线 与x轴交于A,B两点(A在B 的左侧),与y轴交于点 N,过点 A 的直线l: 与y 轴交于点C,与抛物线 的另一个交点为D,已知点 A的坐标为( ,点 D 的坐标为( ,点 P 为抛物线 上一动点(不与点 A,D 重合).
(1)求抛物线和直线l的解析式;
(2)当点 P 在直线l 上方的抛物线上时,过点 P 作. 轴交直线l 于点E,作 轴交直线l于点 F,求. 的最大值;
(3)设M为直线l上的点,探究是否存在点M,使得以点 N,C,M,P 为顶点的四边形为平行四边形 若存在,求出点 M的坐标;若不存在,请说明理由.
解析
(1)将点A,D的坐标分别代入直线和抛物线的解析式,即可求解;
(2)用字母t表示出点P,F的坐标,然后由直线 的解析式,求出 PE 和PF 的关系,然后把 转化为用 PF 表示,即可求解;
(3)分CN,CM,CP 分别为对角线,应用中点坐标公式求解;也可以分 NC 是平行四边形的一条边、NC 是平行四边形的对角线,两种情况分别求解即可.
解(1)将点 A,D的坐标代入直线解析式得
解得
故直线l的解析式为y=-x--1.
将点A,D的坐标代入抛物线解析式,
同理可得抛物线的解析式为
(2)直线l的解析式为y=-x-1,则直线l与x轴的夹角为45°,
即 PE=PF,如答图 1.
设点 P 的坐标为 则点 F 的坐标为(t,-t-1).
P. 8.
∵--2<0,故 PE+PF有最大值,
当t=2,即点 P 的坐标为(2,6)时,其最大值为18;
(3)解法一:设点 P 的坐标为 点 M 的坐标为(n,-n-1).
①当 NC 是平行四边形的对角线时,如答图2,
则 NC的中点坐标为(0, ).
NC的中点即为PM 的中点,
即
解得m=4或m=0(舍去).
故点 P 的坐标为(4,0),点 M的坐标为(-4,3).
②当CM是平行四边形的对角线时,如答图3,
则CM的中点坐标为
CM的中点即为PN 的中点,
即
解得 或
故点 M 坐标为 或
③同理,当CP 是平行四边形的对角线时,
则CP 的中点坐标为
CP的中点即为MN 的中点,
即
解得n=m=4或m=0(舍去).
故点 M的坐标为(4,-5).
综上所述,点 M 的坐标为 或(2- 或(4,-5)或(-4,3).
解法二:NC=5.
①当 NC 是平行四边形的一条边时,
设点 P 的坐标为 则点 M 的坐标为((x, -x-1).
由题意,得 即
解得 或 (舍去)或x=4,
则点 P 的坐标为 或 或
②当 NC 是平行四边形的对角线时,同解法一.
综上所述,点 P 的坐标为 或 或 或
例2.已知抛物线F 的图象经过坐标原点O,且与x轴另一交点为
(1)求抛物线 F 的解析式;
(2)如图1,直线( 与抛物线 F 相交于点 和点 (点 A 在第二象限),求 的值(用含 m的式子表示);
(3)在(2)中,若 设点 是点 A 关于原点O 的对称点,如图2.
①判断△AA'B 的形状,并说明理由;
②平面内是否存在点 P,使得以点 A,B,A',P 为顶点的四边形是菱形 若存在,求出点 P 的坐标;若不存在,请说明理由.
解析
(1)待定系数法即可求出抛物线的解析式;
(2)联立直线和抛物线的解析式组成方程组,求出交点坐标,即可进行求解;
(3)①分别求出三角形三个顶点坐标,利用两点间距离公式求出三边长度即可判断三角形的形状;
②在①的基础上,可以作如下思考,把等腰三角形沿底边翻折,则顶点的对应点与三角形的三个顶点即可构成菱形,所以只需要确定等腰三角形的底边为对角线,求顶点关于对角线的对称点即可,可以结合中点坐标公式进行求解,又因为A,A',B三点确定,所以此题为三点定型问题.
解(1)∵抛物线 的图象经过点(0,0)和
解得抛物线 F 的解析式为
(2)将 代入 得
解得
∴点 A 的坐标为 点 B 的坐标为
∵点 A'是点A 关于原点O的对称点,∴点 A'的坐标为
为等边三角形.理由如下:
∴△AA'B 为等边三角形;
②∵△AA'B 为等边三角形,
∴存在符合题意的点 P,且以点 A,B,A',P 为顶点的菱形分三种情况,设点 P 的坐标为(x,y).
(Ⅰ)当A'B 为对角线时,如答图1,时 PA∥x轴,有 y
解得
∴点 P 的坐标为
(Ⅱ)当AB为对角线时,如答图2,此时 PA∥y轴,有
解得
∴点 P 的坐标为
(Ⅲ)当AA'为对角线时,如答图3,此时PA∥y轴,有
解得
∴点 P 的坐标为
综上所述,平面内存在点 P,使得以点A,B,A',P 为顶点的四边形是菱形,点 P 的坐标为 和
例3.如图,抛物线 经过点A(2,-3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.
(1)求抛物线的解析式;
(2)点 D在y 轴上,且∠BDO=∠BAC,求点 D的坐标;
(3)点 M在抛物线上,点 N 在抛物线的对称轴上,是否存在以点 A,B,M,N 为顶点的四边形是平行四边形 若存在,求出所有符合条件的点 M的坐标;若不存在,请说明理由.
解析
(1)待定系数法即可得到结论;
(2)连接AC,可以求得. 如果 则 是等腰直角三角形,即(
(3)两种方法,方法一:分别以AB,BM,BN为对角线分类讨论,注意此处有 A、B两个定点,属于两点定型;方法二:分别以AB为边,以AB为对角线分类讨论.
解(1)由 得 C(0,-3),∴OC=3.
∵OC=3OB,∴OB=1.∴点B的坐标为(-1,0).
把 A(2,-3),B(-1,0)代入 得
解得
∴抛物线的解析式为
(2)如答图1,连接AC,作 BF⊥AC 交AC 的延长线于点 F.
∵A(2,-3),C(0,-3),∴AF∥x轴.
∴点 F的坐标为(-1,-3).∴BF=3,AF=3.∴∠BAC=45°.
设点 D的坐标为(0,m),则OD=|m|.
∵∠BDO=∠BAC,∴∠BDO=45°.
∴OD=OB=1.∴|m|=1.∴m=±1.
∴点 D 的坐标为(0,1),点 D 的坐标为(0,-1);
(3)设点 M的坐标为( 点 N 的坐标为(1,n).
解法一:①以AB为对角线,如答图2,则MN为另一条对角线,对角线相交于一点,且为对角线中点.x/ n.
解得a=0,n=0.
即点 M的坐标为(0,-3),点 N的坐标为(1,0).
②以BM为对角线,如答图3,则AN为另一条对角线,同①类似可得
xm n.
解得a=4,n=8,
即点 M的坐标为(4,5),点 N 的坐标为(1,8).
③以BN为对角线,如答图4,则AM为另一条对角线,同①类似可得
x, -3.
解得a=-2,n=-2,
即点 M的坐标为(-2,5),点 N的坐标为(1,2).
解法二:①以AB为边,则AB∥MN,AB=MN,如答图5,过M作ME⊥对称轴y于点E,AF⊥x轴于点 F.
∴∠MNE=∠BGF=∠A.
则△ABF≌△NME.
∴NE=AF=3,ME=BF=3.∴|a-1|=3.∴a=4或a=-2.
∴点 M的坐标为(4,5)或(-2,5).
②以AB为对角线, ,如答图 6,
则 N在x 轴上,M与C 重合.
∴点 M的坐标为(0,-3).
综上所述,存在以点A,B,M,N为顶点的四边形是平行四边形,M(4,5)或( 或
精选练习
1.如图,已知二次函数 的图象与x轴交于点A(1,0),B(3,0),与 y轴交于点C.
(1)求二次函数的解析式;
(2)若点 P 为抛物线上的一点,点 F 为对称轴上的一点,且以点 A,B,P,F 为顶点的四边形为平行四边形,求点 P 的坐标.
2.如图,抛物线 的图象经过A(1,0),B(3,0),C(0,6)三点.
(1)求抛物线的解析式;
(2)抛物线的顶点 M与对称轴l上的点 N 关于x 轴对称,直线AN 交抛物线于点 D,直线 BE 交AD 于点 E,若直线 BE将. 的面积分为1:2两部分,求点 E的坐标;
(3)P 为抛物线上的一动点,Q为对称轴上动点,抛物线上是否存在一点 P,使 A、D、P、Q为顶点的四边形为平行四边形 若存在,求出点 P 的坐标;若不存在,请说明理由.
3.如图,在平面直角坐标系中,直线 与x轴交于点A,经过点A的抛物线 的对称轴是
(1)求抛物线的解析式;
(2)平移直线l经过原点O,得到直线m,点 P 是直线m 上任意一点, 轴于点B, 轴于点C,若点 E在线段OB 上,点 F 在线段OC 的延长线上,连接 PE,PF,且 求证:PE
(3)若(2)中的点 P坐标为(6,2),点 E 是x轴上的点,点F 是y轴上的点,当. 时,抛物线上是否存在点Q,使四边形 PEQF 是矩形 如果存在,请求出点 Q的坐标,如果不存在,请说明理由.
4.在平面直角坐标系中,抛物线 经过点 点 M 为抛物线的顶点,点 B 在y 轴上,且( ,直线AB与抛物线在第一象限交于点C(2,6),如图1.
(1)求抛物线的解析式;
(2)直线AB的函数解析式为 ,点 M的坐标为 ,cos∠ABO=_;连接OC,若过点O的直线交线段AC 于点 P,将 的面积分成1:2的两部分,则点 P 的坐标为 ;
(3)在y轴上找一点Q,使得 的周长最小.具体作法如图2,作点 A关于y轴的对称点! 连接 交y轴于点Q,连接AM、AQ,此时 的周长最小.请求出点Q的坐标;
(4)在坐标平面内是否存在点 N,使以点 A、O、C、N 为顶点的四边形是平行四边形 若存在,请直接写出点 N的坐标;若不存在,请说明理由.
精选练习
1.解:(1)用交点式函数解析式得y=(x-1)(x-3)
故所求二次函数的解析式为
(2)①当 AB 为平行四 边 形 一 条 边时,如答图1.
则AB=PF=2,点 P坐标为(4,3).
当点 P 在对称轴左侧时,即点 C 的位置,点 A,B,P,F 为顶点的四边形为平行四边形,
∴点 P 的坐标为(4,3)或(0,3).
②当AB是四边形的对角线时,如答图2.
AB 中点的坐标为(2,0).
设点 P 的横坐标为m,点 F 的横坐标为2,其中点的横坐标为
即 解 得 m=2,故点 P 的坐标为(2,-1).
∴点 P 的坐标为(4,3)或(0,3)或(2,-1).
2. 解:(1)∵抛物线 的图象经过A(1,0),B(3,0),
∴设抛物线的解析式为y=a(x-1)(x-3).
∵抛物线y=a(x-1)(x-3)(a≠0)的图象经过点C(0,6),
∴6=a(0-1)(0-3).
∴a=2.
∴抛物线的解析式为y=2(x-1)(x-3)=2x -8x+6;
∴顶点 M的坐标为(2,-2).
∵抛物线的顶点 M与对称轴l 上的点 N 关于x 轴对称,
∴点 N的坐标为(2,2).
设直线AN的解析式为y=kx+b(k≠0).
由题意,可得
解得
∴直线AN的解析式为y=2x-2.
联立方程组,得
解得
∴点 D的坐标为(4,6).
设点 E的坐标为(m,2m-2).
∵直线 BE将△ABD的面积分为1: 2两部分,
或
或
∴m=2或m=3.
∴点 E的坐标为(2,2)或(3,4);
(3)若 AD为平行四边形的边,
∵以A,D,P,Q为顶点的四边形为平行四边形,
∴AD=PQ.
或.
或xp=2-4+1=-1.
∴点 P 的坐标为(5,16)或(-1,16).
若AD为平行四边形的对角线,
∵以A,D,P,Q为顶点的四边形为平行四边形,
∴AD与PQ互相平分.
∴点 P 的坐标为(3,0).
综上所述,当点 P 坐标为(5,16)或(-1,16)或(3,0)时,以点A,D,P,Q为顶点的四边形为平行四边形.
3. 解:(1)当y=0时, 解得x=4,即点A的坐标为(4,0),抛物线过点 A,对称轴是 得
解得 抛物线的解析式为
(2)∵平移直线l经过原点O,得到直线m,
∴直线 m的解析式为
∵点 P 是直线l上任意一点,
∴设点 P的坐标为(3a,a),则PC=3a,PB=a.
又∵PF=3PE,
∴Rt△PCF∽Rt△PBE.
∴∠FPC=∠EPB.
∵∠CPE+∠EPB=90°,
∴∠FPC+∠CPE=90°.
∴FP⊥PE;
(3)如答图1,点 E 在点 B 的左侧时,设点 E 的坐标为(a,0),
则BE=6-a.
∵CF=3BE=18-3a,
∴OF=20-3a.
∴F(0,20-3a).
∵四边形 PEQF 为矩形,
∴Q,+6=0+a,
Q,+2=20-3a+0.
∴Q,=a-6,
Qy=18-3a.
将点Q的坐标代入抛物线的解析式,得 18-3a 解得a=4或a=8(舍去).
∴点 Q的坐标为(-2,6).
如图,当点 E 在点B 的右侧时,设 E(a,0),则BE=a--6.
∵CF=3BE=3a-18,
∴OF=3a-20.
∴F(0,20-3a).
∵四边形 PEQF 为矩形,
∴Q +6=0+a, Qy+2=20-3a+0.
∴Q,=a-6, Qy=18-3a.
将点Q的坐标代入抛物线的解析式,得18-3a= 解得a=8或a=4(舍去).
∴点Q的坐标为(2,-6).
综上所述,点Q的坐标为(-2,6)或(2,-6).
4.解:(1)将点 A,C的坐标代入抛物线解析式得
解得
故直线AB的解析式为
(2)点A(-4,0),OB=OA=4,故点 B(0,4),
由点A,B的坐标得,直线AB的解析式为y=x+4.
则∠ABO=45°,故
对于 函数的对称轴为x=-2,故点M的坐标为(-2,-2).
OP 将△AOC的面积分成1: 2的两部分,则AP= 或
则 或 即 或 解得yp=2或yp=4.
故点 P的坐标为(-2,2)或(0,4).
(3)△AMQ的周长=AM+AQ+MQ=AM+A'M最小,
点 A'的坐标为(4,0).
设直线 A'M 的解析式为y=kx+b(k≠0),则
解得
故直线 A'M 的解析式为
令x=0,则 故点 Q的坐标为
(4)存在.理由如下:设点 N 的坐标为(m,n),而点A,C,O的坐标分别为(-4,0),(2,6),(0,0).
①当AC 是边时,点 A 向右平移6个单位长度,再向上平移6个单位长度得到点 C,同样点 O(N)向右平移6个单位长度,再向上平移6个单位长度得到点 N(O),即O±6=m,O±6=n,解得m=n=±6,故点 N的坐标为(6,6)或(-6,-6).
②当AC是对角线时,由中点公式,得-4+2=m+0,6+0=n+0.解得m=-2,n=6,故点 N的坐标为(--2,6).
综上所述,点 N 的坐标为(6,6)或(-6,--6)或(--2,6).
解题策略
关于四边形为平行四边形的问题,要分以下几种情况进行讨论:
1.若三点坐标已知,则分别以三点所确定的线段为对角线,利用中点坐标公式进行解答;或者分别以三点所确定的线段为边,利用平行四边形对边平行且相等,利用平移进行解答.
2.若两点的坐标已知,第三点为已知直线(或曲线)上的动点,则用参数表示出第三点的坐标,然后借助对角线讨论法,利用中点坐标公式进行解答.
点 P(a,b)是点 A(xA,yA)与点. 的中点,也可以说点A、B关于点P 成中心对称,则 P 点的坐标为 即
如果四边形ABCD为平行四边形, 因为平行四边形的对角线互相平分,交点为对角线的中点,所以有 整理,得 或
模型一 三点定型
已知二次函数 的图象与x轴交于A,B 两点(A在左侧,B在右侧),与y轴交于C点,顶点为 D.
如图,M为平面内一点,若A,B,C,M为顶点的四边形是平行四边形,直接写出 M点坐标.
思路分析:平行四边形存在性问题,且是三点坐标已知,求第四个点的问题,只要采用对角线讨论法(分别以AB,BC,AC为对角线作平行四边形),即可做到不重、不漏.
模型二 两点定型
已知二次函数 的图象与x轴交于A,B两点(A在左侧,B在右侧),与 y轴交于C点,顶点为 D.
如图,M是x轴上一动点,N 是抛物线上一动点.若以A,C,M,N 为顶点的四边形是平行四边形,直接写出点 M的坐标.
思路分析:平行四边形存在性问题,且是A、C两点坐标已知,求其余两个点的问题,只要采用对角线讨论法(分别以AM,MC,AC为对角线作平行四边形),即可做到不重、不漏.
模型三 一点定型
已知二次函数 的图象与x轴交于A,B两点(A 在左侧,B 在右侧),与y轴交于C点,顶点为 D.
如图,抛物线对称轴与x轴交于点E,M是线段AB 上一动点,且 交抛物线对称轴于点N,P 是抛物线上一点.若以M,N,P,E为顶点的四边形是平行四边形,直接写出点 P 的坐标.
思路分析:平行四边形存在性问题,且是E点坐标已知,求其余三个动点中的一个点的坐标问题,只要采用对角线讨论法(分别以 EM,NE,MN为对角线作平行四边形),即可做到不重、不漏.
模型四 菱形问题
已知二次函数 的图象与x轴交于A,B两点(A在左侧,B在右侧),与y轴交于C点.如图,P 是抛物线对称轴上一动点,Q是坐标系内一点,若四边形 ACQP 是菱形,直接写出点 Q的坐标.
思路分析:将一个等腰三角形沿底边翻折得到的四边形就是菱形,所以只需要将菱形存在性问题转化为等腰三角形存在性问题,再结合平行四边形存在性问题的即可解决.
以 A为顶点,CP 为对角线:
以C为顶点,AP 为对角线:
以 P 为顶点,AC为对角线.
模型五 矩形问题
已知二次函数 的图象与x轴交于A,B两点(A在左侧,B在右侧),与y轴交于点C.如图,P 是抛物线对称轴上一动点,Q是平面内一点,若四边形 ACPQ(按逆时针方向)是矩形,直接写出点 Q的坐标.
思路分析:矩形问题可转化为直角三角形和平行四边形问题来解决,可先确定出直角三角形,再以斜边为对角线补充平行四边形,即可得到矩形.注意字母顺序哦!
以 A 为直角顶点,PC为对角线:
以C为直角顶点,PA为对角线:
以 P 为直角顶点,AC为对角线:
精选例题
例1.如图,抛物线 与x轴交于A,B两点(A在B 的左侧),与y轴交于点 N,过点 A 的直线l: 与y 轴交于点C,与抛物线 的另一个交点为D,已知点 A的坐标为( ,点 D 的坐标为( ,点 P 为抛物线 上一动点(不与点 A,D 重合).
(1)求抛物线和直线l的解析式;
(2)当点 P 在直线l 上方的抛物线上时,过点 P 作. 轴交直线l 于点E,作 轴交直线l于点 F,求. 的最大值;
(3)设M为直线l上的点,探究是否存在点M,使得以点 N,C,M,P 为顶点的四边形为平行四边形 若存在,求出点 M的坐标;若不存在,请说明理由.
解析
(1)将点A,D的坐标分别代入直线和抛物线的解析式,即可求解;
(2)用字母t表示出点P,F的坐标,然后由直线 的解析式,求出 PE 和PF 的关系,然后把 转化为用 PF 表示,即可求解;
(3)分CN,CM,CP 分别为对角线,应用中点坐标公式求解;也可以分 NC 是平行四边形的一条边、NC 是平行四边形的对角线,两种情况分别求解即可.
解(1)将点 A,D的坐标代入直线解析式得
解得
故直线l的解析式为y=-x--1.
将点A,D的坐标代入抛物线解析式,
同理可得抛物线的解析式为
(2)直线l的解析式为y=-x-1,则直线l与x轴的夹角为45°,
即 PE=PF,如答图 1.
设点 P 的坐标为 则点 F 的坐标为(t,-t-1).
P. 8.
∵--2<0,故 PE+PF有最大值,
当t=2,即点 P 的坐标为(2,6)时,其最大值为18;
(3)解法一:设点 P 的坐标为 点 M 的坐标为(n,-n-1).
①当 NC 是平行四边形的对角线时,如答图2,
则 NC的中点坐标为(0, ).
NC的中点即为PM 的中点,
即
解得m=4或m=0(舍去).
故点 P 的坐标为(4,0),点 M的坐标为(-4,3).
②当CM是平行四边形的对角线时,如答图3,
则CM的中点坐标为
CM的中点即为PN 的中点,
即
解得 或
故点 M 坐标为 或
③同理,当CP 是平行四边形的对角线时,
则CP 的中点坐标为
CP的中点即为MN 的中点,
即
解得n=m=4或m=0(舍去).
故点 M的坐标为(4,-5).
综上所述,点 M 的坐标为 或(2- 或(4,-5)或(-4,3).
解法二:NC=5.
①当 NC 是平行四边形的一条边时,
设点 P 的坐标为 则点 M 的坐标为((x, -x-1).
由题意,得 即
解得 或 (舍去)或x=4,
则点 P 的坐标为 或 或
②当 NC 是平行四边形的对角线时,同解法一.
综上所述,点 P 的坐标为 或 或 或
例2.已知抛物线F 的图象经过坐标原点O,且与x轴另一交点为
(1)求抛物线 F 的解析式;
(2)如图1,直线( 与抛物线 F 相交于点 和点 (点 A 在第二象限),求 的值(用含 m的式子表示);
(3)在(2)中,若 设点 是点 A 关于原点O 的对称点,如图2.
①判断△AA'B 的形状,并说明理由;
②平面内是否存在点 P,使得以点 A,B,A',P 为顶点的四边形是菱形 若存在,求出点 P 的坐标;若不存在,请说明理由.
解析
(1)待定系数法即可求出抛物线的解析式;
(2)联立直线和抛物线的解析式组成方程组,求出交点坐标,即可进行求解;
(3)①分别求出三角形三个顶点坐标,利用两点间距离公式求出三边长度即可判断三角形的形状;
②在①的基础上,可以作如下思考,把等腰三角形沿底边翻折,则顶点的对应点与三角形的三个顶点即可构成菱形,所以只需要确定等腰三角形的底边为对角线,求顶点关于对角线的对称点即可,可以结合中点坐标公式进行求解,又因为A,A',B三点确定,所以此题为三点定型问题.
解(1)∵抛物线 的图象经过点(0,0)和
解得抛物线 F 的解析式为
(2)将 代入 得
解得
∴点 A 的坐标为 点 B 的坐标为
∵点 A'是点A 关于原点O的对称点,∴点 A'的坐标为
为等边三角形.理由如下:
∴△AA'B 为等边三角形;
②∵△AA'B 为等边三角形,
∴存在符合题意的点 P,且以点 A,B,A',P 为顶点的菱形分三种情况,设点 P 的坐标为(x,y).
(Ⅰ)当A'B 为对角线时,如答图1,时 PA∥x轴,有 y
解得
∴点 P 的坐标为
(Ⅱ)当AB为对角线时,如答图2,此时 PA∥y轴,有
解得
∴点 P 的坐标为
(Ⅲ)当AA'为对角线时,如答图3,此时PA∥y轴,有
解得
∴点 P 的坐标为
综上所述,平面内存在点 P,使得以点A,B,A',P 为顶点的四边形是菱形,点 P 的坐标为 和
例3.如图,抛物线 经过点A(2,-3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.
(1)求抛物线的解析式;
(2)点 D在y 轴上,且∠BDO=∠BAC,求点 D的坐标;
(3)点 M在抛物线上,点 N 在抛物线的对称轴上,是否存在以点 A,B,M,N 为顶点的四边形是平行四边形 若存在,求出所有符合条件的点 M的坐标;若不存在,请说明理由.
解析
(1)待定系数法即可得到结论;
(2)连接AC,可以求得. 如果 则 是等腰直角三角形,即(
(3)两种方法,方法一:分别以AB,BM,BN为对角线分类讨论,注意此处有 A、B两个定点,属于两点定型;方法二:分别以AB为边,以AB为对角线分类讨论.
解(1)由 得 C(0,-3),∴OC=3.
∵OC=3OB,∴OB=1.∴点B的坐标为(-1,0).
把 A(2,-3),B(-1,0)代入 得
解得
∴抛物线的解析式为
(2)如答图1,连接AC,作 BF⊥AC 交AC 的延长线于点 F.
∵A(2,-3),C(0,-3),∴AF∥x轴.
∴点 F的坐标为(-1,-3).∴BF=3,AF=3.∴∠BAC=45°.
设点 D的坐标为(0,m),则OD=|m|.
∵∠BDO=∠BAC,∴∠BDO=45°.
∴OD=OB=1.∴|m|=1.∴m=±1.
∴点 D 的坐标为(0,1),点 D 的坐标为(0,-1);
(3)设点 M的坐标为( 点 N 的坐标为(1,n).
解法一:①以AB为对角线,如答图2,则MN为另一条对角线,对角线相交于一点,且为对角线中点.x/ n.
解得a=0,n=0.
即点 M的坐标为(0,-3),点 N的坐标为(1,0).
②以BM为对角线,如答图3,则AN为另一条对角线,同①类似可得
xm n.
解得a=4,n=8,
即点 M的坐标为(4,5),点 N 的坐标为(1,8).
③以BN为对角线,如答图4,则AM为另一条对角线,同①类似可得
x, -3.
解得a=-2,n=-2,
即点 M的坐标为(-2,5),点 N的坐标为(1,2).
解法二:①以AB为边,则AB∥MN,AB=MN,如答图5,过M作ME⊥对称轴y于点E,AF⊥x轴于点 F.
∴∠MNE=∠BGF=∠A.
则△ABF≌△NME.
∴NE=AF=3,ME=BF=3.∴|a-1|=3.∴a=4或a=-2.
∴点 M的坐标为(4,5)或(-2,5).
②以AB为对角线, ,如答图 6,
则 N在x 轴上,M与C 重合.
∴点 M的坐标为(0,-3).
综上所述,存在以点A,B,M,N为顶点的四边形是平行四边形,M(4,5)或( 或
精选练习
1.如图,已知二次函数 的图象与x轴交于点A(1,0),B(3,0),与 y轴交于点C.
(1)求二次函数的解析式;
(2)若点 P 为抛物线上的一点,点 F 为对称轴上的一点,且以点 A,B,P,F 为顶点的四边形为平行四边形,求点 P 的坐标.
2.如图,抛物线 的图象经过A(1,0),B(3,0),C(0,6)三点.
(1)求抛物线的解析式;
(2)抛物线的顶点 M与对称轴l上的点 N 关于x 轴对称,直线AN 交抛物线于点 D,直线 BE 交AD 于点 E,若直线 BE将. 的面积分为1:2两部分,求点 E的坐标;
(3)P 为抛物线上的一动点,Q为对称轴上动点,抛物线上是否存在一点 P,使 A、D、P、Q为顶点的四边形为平行四边形 若存在,求出点 P 的坐标;若不存在,请说明理由.
3.如图,在平面直角坐标系中,直线 与x轴交于点A,经过点A的抛物线 的对称轴是
(1)求抛物线的解析式;
(2)平移直线l经过原点O,得到直线m,点 P 是直线m 上任意一点, 轴于点B, 轴于点C,若点 E在线段OB 上,点 F 在线段OC 的延长线上,连接 PE,PF,且 求证:PE
(3)若(2)中的点 P坐标为(6,2),点 E 是x轴上的点,点F 是y轴上的点,当. 时,抛物线上是否存在点Q,使四边形 PEQF 是矩形 如果存在,请求出点 Q的坐标,如果不存在,请说明理由.
4.在平面直角坐标系中,抛物线 经过点 点 M 为抛物线的顶点,点 B 在y 轴上,且( ,直线AB与抛物线在第一象限交于点C(2,6),如图1.
(1)求抛物线的解析式;
(2)直线AB的函数解析式为 ,点 M的坐标为 ,cos∠ABO=_;连接OC,若过点O的直线交线段AC 于点 P,将 的面积分成1:2的两部分,则点 P 的坐标为 ;
(3)在y轴上找一点Q,使得 的周长最小.具体作法如图2,作点 A关于y轴的对称点! 连接 交y轴于点Q,连接AM、AQ,此时 的周长最小.请求出点Q的坐标;
(4)在坐标平面内是否存在点 N,使以点 A、O、C、N 为顶点的四边形是平行四边形 若存在,请直接写出点 N的坐标;若不存在,请说明理由.
精选练习
1.解:(1)用交点式函数解析式得y=(x-1)(x-3)
故所求二次函数的解析式为
(2)①当 AB 为平行四 边 形 一 条 边时,如答图1.
则AB=PF=2,点 P坐标为(4,3).
当点 P 在对称轴左侧时,即点 C 的位置,点 A,B,P,F 为顶点的四边形为平行四边形,
∴点 P 的坐标为(4,3)或(0,3).
②当AB是四边形的对角线时,如答图2.
AB 中点的坐标为(2,0).
设点 P 的横坐标为m,点 F 的横坐标为2,其中点的横坐标为
即 解 得 m=2,故点 P 的坐标为(2,-1).
∴点 P 的坐标为(4,3)或(0,3)或(2,-1).
2. 解:(1)∵抛物线 的图象经过A(1,0),B(3,0),
∴设抛物线的解析式为y=a(x-1)(x-3).
∵抛物线y=a(x-1)(x-3)(a≠0)的图象经过点C(0,6),
∴6=a(0-1)(0-3).
∴a=2.
∴抛物线的解析式为y=2(x-1)(x-3)=2x -8x+6;
∴顶点 M的坐标为(2,-2).
∵抛物线的顶点 M与对称轴l 上的点 N 关于x 轴对称,
∴点 N的坐标为(2,2).
设直线AN的解析式为y=kx+b(k≠0).
由题意,可得
解得
∴直线AN的解析式为y=2x-2.
联立方程组,得
解得
∴点 D的坐标为(4,6).
设点 E的坐标为(m,2m-2).
∵直线 BE将△ABD的面积分为1: 2两部分,
或
或
∴m=2或m=3.
∴点 E的坐标为(2,2)或(3,4);
(3)若 AD为平行四边形的边,
∵以A,D,P,Q为顶点的四边形为平行四边形,
∴AD=PQ.
或.
或xp=2-4+1=-1.
∴点 P 的坐标为(5,16)或(-1,16).
若AD为平行四边形的对角线,
∵以A,D,P,Q为顶点的四边形为平行四边形,
∴AD与PQ互相平分.
∴点 P 的坐标为(3,0).
综上所述,当点 P 坐标为(5,16)或(-1,16)或(3,0)时,以点A,D,P,Q为顶点的四边形为平行四边形.
3. 解:(1)当y=0时, 解得x=4,即点A的坐标为(4,0),抛物线过点 A,对称轴是 得
解得 抛物线的解析式为
(2)∵平移直线l经过原点O,得到直线m,
∴直线 m的解析式为
∵点 P 是直线l上任意一点,
∴设点 P的坐标为(3a,a),则PC=3a,PB=a.
又∵PF=3PE,
∴Rt△PCF∽Rt△PBE.
∴∠FPC=∠EPB.
∵∠CPE+∠EPB=90°,
∴∠FPC+∠CPE=90°.
∴FP⊥PE;
(3)如答图1,点 E 在点 B 的左侧时,设点 E 的坐标为(a,0),
则BE=6-a.
∵CF=3BE=18-3a,
∴OF=20-3a.
∴F(0,20-3a).
∵四边形 PEQF 为矩形,
∴Q,+6=0+a,
Q,+2=20-3a+0.
∴Q,=a-6,
Qy=18-3a.
将点Q的坐标代入抛物线的解析式,得 18-3a 解得a=4或a=8(舍去).
∴点 Q的坐标为(-2,6).
如图,当点 E 在点B 的右侧时,设 E(a,0),则BE=a--6.
∵CF=3BE=3a-18,
∴OF=3a-20.
∴F(0,20-3a).
∵四边形 PEQF 为矩形,
∴Q +6=0+a, Qy+2=20-3a+0.
∴Q,=a-6, Qy=18-3a.
将点Q的坐标代入抛物线的解析式,得18-3a= 解得a=8或a=4(舍去).
∴点Q的坐标为(2,-6).
综上所述,点Q的坐标为(-2,6)或(2,-6).
4.解:(1)将点 A,C的坐标代入抛物线解析式得
解得
故直线AB的解析式为
(2)点A(-4,0),OB=OA=4,故点 B(0,4),
由点A,B的坐标得,直线AB的解析式为y=x+4.
则∠ABO=45°,故
对于 函数的对称轴为x=-2,故点M的坐标为(-2,-2).
OP 将△AOC的面积分成1: 2的两部分,则AP= 或
则 或 即 或 解得yp=2或yp=4.
故点 P的坐标为(-2,2)或(0,4).
(3)△AMQ的周长=AM+AQ+MQ=AM+A'M最小,
点 A'的坐标为(4,0).
设直线 A'M 的解析式为y=kx+b(k≠0),则
解得
故直线 A'M 的解析式为
令x=0,则 故点 Q的坐标为
(4)存在.理由如下:设点 N 的坐标为(m,n),而点A,C,O的坐标分别为(-4,0),(2,6),(0,0).
①当AC 是边时,点 A 向右平移6个单位长度,再向上平移6个单位长度得到点 C,同样点 O(N)向右平移6个单位长度,再向上平移6个单位长度得到点 N(O),即O±6=m,O±6=n,解得m=n=±6,故点 N的坐标为(6,6)或(-6,-6).
②当AC是对角线时,由中点公式,得-4+2=m+0,6+0=n+0.解得m=-2,n=6,故点 N的坐标为(--2,6).
综上所述,点 N 的坐标为(6,6)或(-6,--6)或(--2,6).
同课章节目录
