2024年陕西省咸阳市永寿县部分学校中考模拟数学试题(含答案)
文档属性
| 名称 | 2024年陕西省咸阳市永寿县部分学校中考模拟数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-20 10:20:05 | ||
图片预览



文档简介
2024年陕西省初中学业水平考试信心提升卷
数学试卷
注意事项:
1. 本试卷分为第一部分(选择题)和第二部分(非选择题).全卷共6页,总分120分.考试时间120分钟.
2. 领到试卷和答题卡后,请用0.5毫米黑色墨水签字笔,分别在试卷和答题卡上填写姓名和准考证号,同时用2B铅笔在答题卡上填涂对应的试卷类型信息点(A或B).
3. 请在答题卡上各题的指定区域内作答,否则作答无效.
4. 作图时,先用铅笔作图,再用规定签字笔描黑.
5. 考试结束,本试卷和答题卡一并交回.
第一部分(选择题 共24分)
一、选择题(共8小题,每小题3分,计24分.每小题只有一个选项是符合题意的)
1. 的绝对值是( )
A. B. C. D.
2. 如图,点E、F分别在AB、CD上,连接CE、BF,若,,则( )
(第2题图)
A. B. C. D.
3. 计算的结果是( )
A. B. C. D.
4. 如图,在菱形ABCD中,连接AC、BD,若,则的度数为( )
(第4题图)
A. B. C. D.
5. 一次函数(k为常数,)的图象不经过第四象限,则k的取值范围是( )
A. B. C. D.
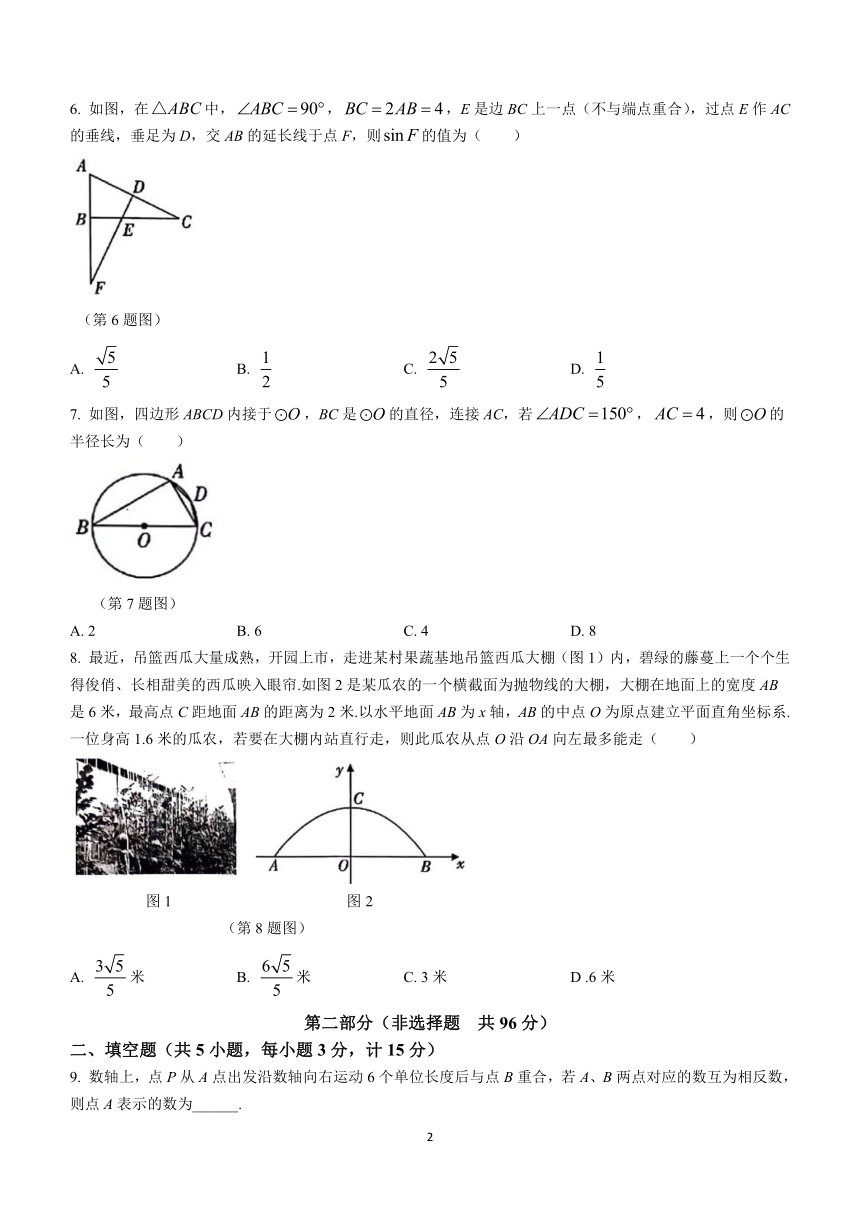
6. 如图,在中,,,E是边BC上一点(不与端点重合),过点E作AC的垂线,垂足为D,交AB的延长线于点F,则的值为( )
(第6题图)
A. B. C. D.
7. 如图,四边形ABCD内接于,BC是的直径,连接AC,若,,则的半径长为( )
(第7题图)
A. 2 B. 6 C. 4 D. 8
8. 最近,吊篮西瓜大量成熟,开园上市,走进某村果蔬基地吊篮西瓜大棚(图1)内,碧绿的藤蔓上一个个生得俊俏、长相甜美的西瓜映入眼帘.如图2是某瓜农的一个横截面为抛物线的大棚,大棚在地面上的宽度AB是6米,最高点C距地面AB的距离为2米.以水平地面AB为x轴,AB的中点O为原点建立平面直角坐标系.一位身高1.6米的瓜农,若要在大棚内站直行走,则此瓜农从点O沿OA向左最多能走( )
图1 图2
(第8题图)
A. 米 B. 米 C. 3米 D .6米
第二部分(非选择题 共96分)
二、填空题(共5小题,每小题3分,计15分)
9. 数轴上,点P从A点出发沿数轴向右运动6个单位长度后与点B重合,若A、B两点对应的数互为相反数,则点A表示的数为______.
10. 如图,点O是正八边形ABCDEFGH的中心,连接OA、OB,则______.
(第10题图)
11. 《九章算术》中记载了这样一个数学问题:今有甲发长安,五日至齐;乙发齐,七日至长安.今乙发已先二日,甲仍发长安.问几何日相逢?译文:甲从长安出发,5日到齐国;乙从齐国出发,7日到长安.现乙从齐国先出发2日,甲才从长安出发.问甲出发几日,甲乙相逢?设甲出发x日,甲乙相逢,可列方程为______.
12. 若点、均在反比例函数(k为常数)的图象上,则m,n的大小关系为m______n.(填“>”“=”或“<”)
13. 如图,在矩形ABCD中,,,点P是矩形内一个动点,连接PA、PB、PC.若,则的最小值为______.
(第13题图)
三、解答题(共13小题,计81分.解答应写出过程)
14.(本题满分5分)
求不等式组:的整数解.
15.(本题满分5分)
计算:.
16.(本题满分5分)
解方程:.
17.(本题满分5分)
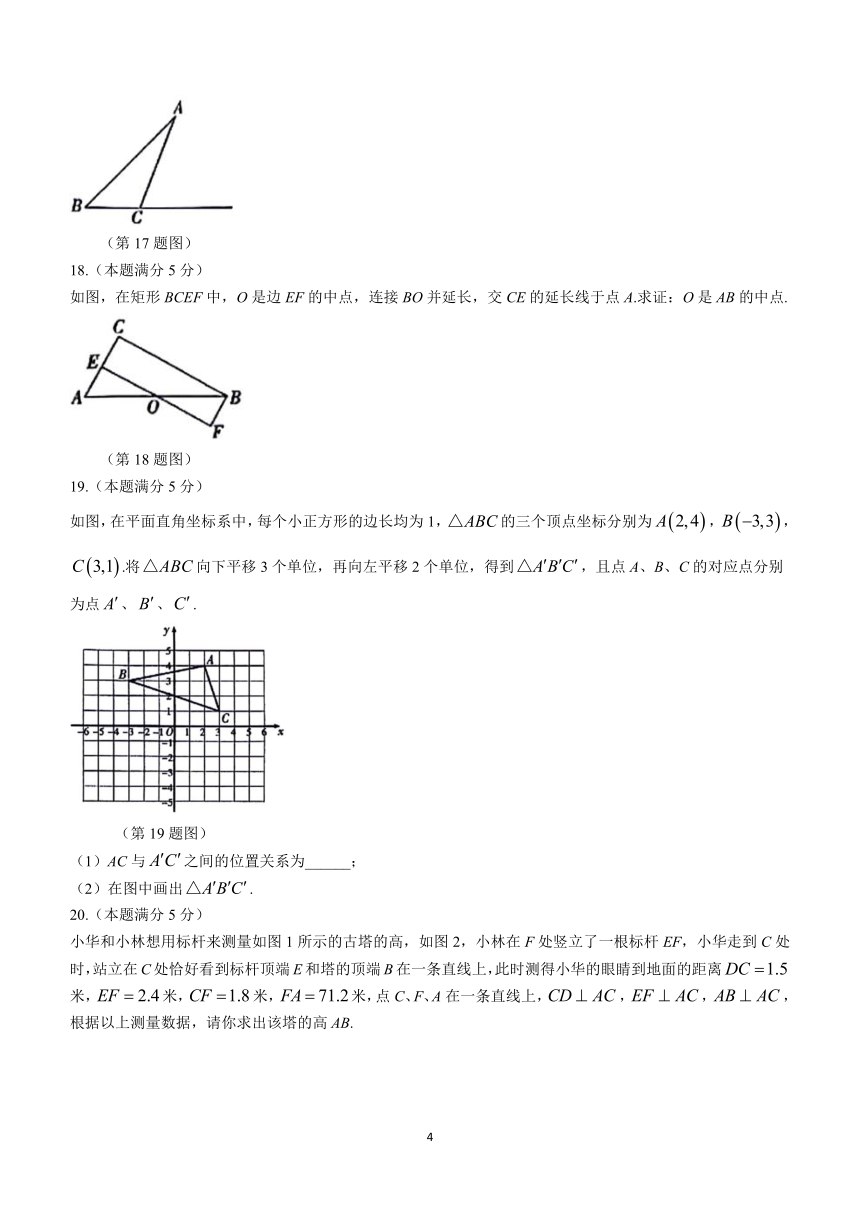
如图,已知,,请用尺规作图法在BC的延长线上找一点D,连接AD,使得.(不写作法,保留作图痕迹)
(第17题图)
18.(本题满分5分)
如图,在矩形BCEF中,O是边EF的中点,连接BO并延长,交CE的延长线于点A.求证:O是AB的中点.
(第18题图)
19.(本题满分5分)
如图,在平面直角坐标系中,每个小正方形的边长均为1,的三个顶点坐标分别为,,.将向下平移3个单位,再向左平移2个单位,得到,且点A、B、C的对应点分别为点、、.
(第19题图)
(1)AC与之间的位置关系为______;
(2)在图中画出.
20.(本题满分5分)
小华和小林想用标杆来测量如图1所示的古塔的高,如图2,小林在F处竖立了一根标杆EF,小华走到C处时,站立在C处恰好看到标杆顶端E和塔的顶端B在一条直线上,此时测得小华的眼睛到地面的距离米,米,米,米,点C、F、A在一条直线上,,,,根据以上测量数据,请你求出该塔的高AB.
图1 图2
(第20题图)
21.(本题满分6分)
六一国际儿童节,某景区为孩子们精心打造了一场以“童心童梦,趣玩六一”为主题的亲子嘉年华活动.该景区内有一摊位推出了掷硬币,摸小球赢玩偶游戏,他准备了一枚硬币和四个小球,在这四个小球上分别标记数字1、2、3、4,每个小球除数字不同外其余均相同,将这四个小球放入一个不透明的箱子中.
(1)若将硬币随机掷30次,其中正面朝上的次数为12次,则在这30次掷硬币中,该硬币正面朝上的频率为______;
(2)游戏规定:参与者先掷硬币,若该硬币正面朝上,则所得的数字记为1;若该硬币反面朝上,则所得的数字记为0.接下来,参与者再从箱子里的四个小球中随机摸出一个,记录所摸小球上的数字(即为所得数字).如果两次所得的数字之和大于3,则可赢得玩偶,其余情况,不能赢得玩偶.乐乐参加了一次赢玩偶游戏,请用列表或画树状图的方法求他获得玩偶的概率.
22.(本题满分7分)
“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.某单位计划在端午节前购买某品牌的粽子发放给员工.经询价,已知甲、乙两超市都以80元/盒的价格销售该品牌粽子,并且同时在做促销活动.
甲超市:办理本超市会员卡(卡费200元),商品全部打七折销售.
乙超市:购买同种商品超过一定数量后,超过的部分打折销售.
活动期间,若该单位购买此品牌粽子x盒,在甲、乙超市所需总费用分别为元、元,与x之间的函数图象如图所示,回答下列问题:
(第22题图)
(1)分别求出、与之间的函数关系式;
(2)若该单位准备购买100盒粽子,你认为在哪家超市购买更划算?
23.(本题满分7分)
2024年,是中国共产党成立第103周年,意义非凡.某校为了解本校学生党史知识的掌握情况,组织了有关党史知识的竞答活动,并随机抽取了30名同学的成绩,形成了如下的调查报告.
课题 ××学校学生对党史知识掌握情况
调查方式 抽样调查
调查对象 ××学校学生
数据的整理与描述 分组成绩x(分)频数A5B7CnD7(第23题图)
调查结论 ……
请根据以上调查报告,解答下列问题:
(1)上述表格中,______,所抽取学生成绩的中位数落在______组;
(2)若该校有1200名学生参加了此次竞答活动,请你估计成绩不低于90分的学生有多少名?
(3)针对此次党史知识的竞答活动,请结合上述调查报告,写出一条你获取到的信息.
24.(本题满分8分)
如图,AB是的直径,CD是弦,AB与CD相交于点M,点A是的中点,连接AC、AD,N为DC延长线上一点,连接NO并延长,交AD的延长线于点P,连接BP,.
(第24题图)
(1)求证:BP为的切线;
(2)若M为OA的中点,,求BP的长.
25.(本题满分8分)
如图,抛物线L:(a、c为常数,)经过点、,顶点为P,连接AP.
(第25题图)
(1)求AP的长;
(2)将抛物线L沿x轴或沿y轴平移若干个单位长度得到抛物线,点A的对应点为,点P的对应点为,当四边形是面积为12的平行四边形,且点在y轴的左侧时,求平移后得到的抛物线的表达式.
26.(本题满分10分)
【问题提出】
(1)如图1,在中,作AB的垂直平分线l,交AC于E,交AB于F,若,连接BE,则的度数为______;
【问题探究】
(2)如图2,在正方形ABCD中,点E是对角线AC上的一点(不与端点重合),连接DE.过点E作,交边AB于点F,以DE,EF为邻边作矩形DEFG.求证:四边形DEFG是正方形;
【问题解决】
(3)如图3,现有一块板材,,.工人师傅想用这块板材裁出一个型部件,并要求.工人师傅在这块板材上的作法如下:
①作AC的垂直平分线l,交AB于E,交AC于F;
②在EF上截取;
③连接BD、CD,得.
请问,若按上述作法,裁得的型部件是否符合要求?请证明你的结论.
图1 图2 图3
(第26题图)
2024年陕西省初中学业水平考试信心提升卷
数学试卷参考答案
一、选择题(共8小题,每小题3分,计24分.每小题只有一个选项是符合题意的)
1. D 2. B 3. B 4. C 5. D 6. A 7. C 8. A
二、填空题(共5小题,每小题3分,计15分)
9. -3 10. 45 11. (其他形式正确也可) 12. <
13. 【解析】根据题意可得点P在矩形内以B为圆心,4为半径的圆弧上运动,在线段BC上取一点M,使得,连接MP、AM,于是有,根据相似三角形的判定可得,则,即,∴.当且仅当A、P、M三点共线时等号成立,利用勾股定理求出AM,即可求解.
三、解答题(共13小题,计81分.解答应写出过程)
14. 解:解得:,……(2分)
解得:,……(3分)
∴不等式组的解集为,……(4分)
∴不等式组的整数解是:-1,0. ……(5分)
15. 解:原式……(3分)
.……(5分)
16. 解:去分母,得,……(2分)
解得:,……(4分)
检验:当时,,
∴是原方程的根.……(5分)
17. 解:如图,点D即为所求.……(5分)
注:①答案中线条为实线或虚线均不扣分;②没有写出结论不扣分;③作法不唯一.
18. 证明:在矩形BCEF中,,……(1分)
∴,
∵O是边EF的中点,∴,……(2分)
在和中,,,,
∴.……(4分)
∴,即O是AB的中点.……(5分)
19. 解:(1)(或平行).……(2分)
(2)如图所示.……(5分)
20. 解:如图,过D作于P,交EF于N,
则,,
,,……(1分)
由题意得,,,
∴,……(3分)
∴,即,
∴,……(4分)
∴,
答:该塔的高AB为38米.……(5分)
注:算出,没有单位,没有答语不扣分.
21. 解:(1)0.4.……(2分)
(2)画树状图如下:……(4分)
由图知,一共有8种等可能的情况,其中所得数字之和大于3的有3种,
∴他获得玩偶的概率是.……(6分)
注:①在(2)中如果求出的概率正确,但没有列表格或画树状图扣2分;求出概率正确,若列表或画树状图后没有就结果作出说明不扣分;②在(2)中若运用枚举法直接列举出8种等可能结果,只要结果正确,不扣分.
22. 解:(1)根据题意,得.……(1分)
当时,设,
由题意得:,解得,
∴.……(4分)
(2)当时,,……(5分)
,
∵,
∴在甲超市购买更划算.……(7分)
23. 解:(1)11.……(2分)
C(或)……(4分)
(2)(名).
∴估计成绩不低于90分的学生有280名.……(6分)
(3)所抽取学生中,A组的学生人数占所抽取学生人数的.……(7分)
注:①(2)中没有答语、不带单位均不扣分;②(2)中没有计算过程扣1分;③(3)中答案不唯一,合理即可.
24.(1)证明:∵点A是的中点,
∴,∴,……(1分)
∵AB是的直径,,
∴,……(2分)
∴,
∵,∴,
∵,∴,……(3分)
∴BP为的切线.……(4分)
(2)解:∵,
∴,,
∴,……(6分)
∴,
∵M为OA的中点,∴,
∵,∴,
∴.……(8分)
25. 解:(1)将、代入中,得
,解得,
∴抛物线L的表达式为.……(2分)
∴顶点.……(3分)
过点P作轴于点D,则,
∵,,,
∴,,
∴.……(4分)
(2)由题意知,四边形是面积为12的平行四边形,
当抛物线沿x轴平移时,可得点在x轴上,
由于,即要使的面积为12,只需,
∵点在y轴左侧,
∴抛物线L沿x轴向左平移3个单位长度可得抛物线,
此时,抛物线的表达式为;……(6分)
当抛物线沿y轴平移时,可得点在直线DP上,
由于,要使的面积为12,只需,
∴抛物线L沿y轴向上或向下平移4个单位长度可得抛物线,
此时,抛物线的表达式为或.
综上,抛物线的表达式为或或.……(8分)
注:(2)中抛物线表达式为其他形式正确均可.
26. 解:(1)45.……(1分)
(2)证明:如图2,过点E作于M,于N.
∵四边形ABCD是正方形,
∴,,……(2分)
∵于M,于N,
∴,
∵,
∴四边形ANEM是矩形,……(3分)
∵,
∴,
∴,
∵,
∴,……(4分)
∴,
∵四边形DEFG是矩形,
∴四边形DEFG是正方形.……(5分)
图2
(3)如图3,过点A作于点G,过点D作于点M,
作于点N,连接AD,
∵EF是线段AC的垂直平分线,,
∴,,∴,
∵,,
∴点G为BC的中点,∴,
∴,
∵,,,∴,
∴四边形DNGM为矩形,……(7分)
∴,∴.
在和中,,,,
∴,……(8分)
∴,,
∴四边形DNGM为正方形,……(9分)
∴,
设,则,
∴,即,
解得,∴,
∴,
∴是等腰直角三角形,且,即.
故裁得的型部件符合要求.……(10分)
图3
数学试卷
注意事项:
1. 本试卷分为第一部分(选择题)和第二部分(非选择题).全卷共6页,总分120分.考试时间120分钟.
2. 领到试卷和答题卡后,请用0.5毫米黑色墨水签字笔,分别在试卷和答题卡上填写姓名和准考证号,同时用2B铅笔在答题卡上填涂对应的试卷类型信息点(A或B).
3. 请在答题卡上各题的指定区域内作答,否则作答无效.
4. 作图时,先用铅笔作图,再用规定签字笔描黑.
5. 考试结束,本试卷和答题卡一并交回.
第一部分(选择题 共24分)
一、选择题(共8小题,每小题3分,计24分.每小题只有一个选项是符合题意的)
1. 的绝对值是( )
A. B. C. D.
2. 如图,点E、F分别在AB、CD上,连接CE、BF,若,,则( )
(第2题图)
A. B. C. D.
3. 计算的结果是( )
A. B. C. D.
4. 如图,在菱形ABCD中,连接AC、BD,若,则的度数为( )
(第4题图)
A. B. C. D.
5. 一次函数(k为常数,)的图象不经过第四象限,则k的取值范围是( )
A. B. C. D.
6. 如图,在中,,,E是边BC上一点(不与端点重合),过点E作AC的垂线,垂足为D,交AB的延长线于点F,则的值为( )
(第6题图)
A. B. C. D.
7. 如图,四边形ABCD内接于,BC是的直径,连接AC,若,,则的半径长为( )
(第7题图)
A. 2 B. 6 C. 4 D. 8
8. 最近,吊篮西瓜大量成熟,开园上市,走进某村果蔬基地吊篮西瓜大棚(图1)内,碧绿的藤蔓上一个个生得俊俏、长相甜美的西瓜映入眼帘.如图2是某瓜农的一个横截面为抛物线的大棚,大棚在地面上的宽度AB是6米,最高点C距地面AB的距离为2米.以水平地面AB为x轴,AB的中点O为原点建立平面直角坐标系.一位身高1.6米的瓜农,若要在大棚内站直行走,则此瓜农从点O沿OA向左最多能走( )
图1 图2
(第8题图)
A. 米 B. 米 C. 3米 D .6米
第二部分(非选择题 共96分)
二、填空题(共5小题,每小题3分,计15分)
9. 数轴上,点P从A点出发沿数轴向右运动6个单位长度后与点B重合,若A、B两点对应的数互为相反数,则点A表示的数为______.
10. 如图,点O是正八边形ABCDEFGH的中心,连接OA、OB,则______.
(第10题图)
11. 《九章算术》中记载了这样一个数学问题:今有甲发长安,五日至齐;乙发齐,七日至长安.今乙发已先二日,甲仍发长安.问几何日相逢?译文:甲从长安出发,5日到齐国;乙从齐国出发,7日到长安.现乙从齐国先出发2日,甲才从长安出发.问甲出发几日,甲乙相逢?设甲出发x日,甲乙相逢,可列方程为______.
12. 若点、均在反比例函数(k为常数)的图象上,则m,n的大小关系为m______n.(填“>”“=”或“<”)
13. 如图,在矩形ABCD中,,,点P是矩形内一个动点,连接PA、PB、PC.若,则的最小值为______.
(第13题图)
三、解答题(共13小题,计81分.解答应写出过程)
14.(本题满分5分)
求不等式组:的整数解.
15.(本题满分5分)
计算:.
16.(本题满分5分)
解方程:.
17.(本题满分5分)
如图,已知,,请用尺规作图法在BC的延长线上找一点D,连接AD,使得.(不写作法,保留作图痕迹)
(第17题图)
18.(本题满分5分)
如图,在矩形BCEF中,O是边EF的中点,连接BO并延长,交CE的延长线于点A.求证:O是AB的中点.
(第18题图)
19.(本题满分5分)
如图,在平面直角坐标系中,每个小正方形的边长均为1,的三个顶点坐标分别为,,.将向下平移3个单位,再向左平移2个单位,得到,且点A、B、C的对应点分别为点、、.
(第19题图)
(1)AC与之间的位置关系为______;
(2)在图中画出.
20.(本题满分5分)
小华和小林想用标杆来测量如图1所示的古塔的高,如图2,小林在F处竖立了一根标杆EF,小华走到C处时,站立在C处恰好看到标杆顶端E和塔的顶端B在一条直线上,此时测得小华的眼睛到地面的距离米,米,米,米,点C、F、A在一条直线上,,,,根据以上测量数据,请你求出该塔的高AB.
图1 图2
(第20题图)
21.(本题满分6分)
六一国际儿童节,某景区为孩子们精心打造了一场以“童心童梦,趣玩六一”为主题的亲子嘉年华活动.该景区内有一摊位推出了掷硬币,摸小球赢玩偶游戏,他准备了一枚硬币和四个小球,在这四个小球上分别标记数字1、2、3、4,每个小球除数字不同外其余均相同,将这四个小球放入一个不透明的箱子中.
(1)若将硬币随机掷30次,其中正面朝上的次数为12次,则在这30次掷硬币中,该硬币正面朝上的频率为______;
(2)游戏规定:参与者先掷硬币,若该硬币正面朝上,则所得的数字记为1;若该硬币反面朝上,则所得的数字记为0.接下来,参与者再从箱子里的四个小球中随机摸出一个,记录所摸小球上的数字(即为所得数字).如果两次所得的数字之和大于3,则可赢得玩偶,其余情况,不能赢得玩偶.乐乐参加了一次赢玩偶游戏,请用列表或画树状图的方法求他获得玩偶的概率.
22.(本题满分7分)
“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.某单位计划在端午节前购买某品牌的粽子发放给员工.经询价,已知甲、乙两超市都以80元/盒的价格销售该品牌粽子,并且同时在做促销活动.
甲超市:办理本超市会员卡(卡费200元),商品全部打七折销售.
乙超市:购买同种商品超过一定数量后,超过的部分打折销售.
活动期间,若该单位购买此品牌粽子x盒,在甲、乙超市所需总费用分别为元、元,与x之间的函数图象如图所示,回答下列问题:
(第22题图)
(1)分别求出、与之间的函数关系式;
(2)若该单位准备购买100盒粽子,你认为在哪家超市购买更划算?
23.(本题满分7分)
2024年,是中国共产党成立第103周年,意义非凡.某校为了解本校学生党史知识的掌握情况,组织了有关党史知识的竞答活动,并随机抽取了30名同学的成绩,形成了如下的调查报告.
课题 ××学校学生对党史知识掌握情况
调查方式 抽样调查
调查对象 ××学校学生
数据的整理与描述 分组成绩x(分)频数A5B7CnD7(第23题图)
调查结论 ……
请根据以上调查报告,解答下列问题:
(1)上述表格中,______,所抽取学生成绩的中位数落在______组;
(2)若该校有1200名学生参加了此次竞答活动,请你估计成绩不低于90分的学生有多少名?
(3)针对此次党史知识的竞答活动,请结合上述调查报告,写出一条你获取到的信息.
24.(本题满分8分)
如图,AB是的直径,CD是弦,AB与CD相交于点M,点A是的中点,连接AC、AD,N为DC延长线上一点,连接NO并延长,交AD的延长线于点P,连接BP,.
(第24题图)
(1)求证:BP为的切线;
(2)若M为OA的中点,,求BP的长.
25.(本题满分8分)
如图,抛物线L:(a、c为常数,)经过点、,顶点为P,连接AP.
(第25题图)
(1)求AP的长;
(2)将抛物线L沿x轴或沿y轴平移若干个单位长度得到抛物线,点A的对应点为,点P的对应点为,当四边形是面积为12的平行四边形,且点在y轴的左侧时,求平移后得到的抛物线的表达式.
26.(本题满分10分)
【问题提出】
(1)如图1,在中,作AB的垂直平分线l,交AC于E,交AB于F,若,连接BE,则的度数为______;
【问题探究】
(2)如图2,在正方形ABCD中,点E是对角线AC上的一点(不与端点重合),连接DE.过点E作,交边AB于点F,以DE,EF为邻边作矩形DEFG.求证:四边形DEFG是正方形;
【问题解决】
(3)如图3,现有一块板材,,.工人师傅想用这块板材裁出一个型部件,并要求.工人师傅在这块板材上的作法如下:
①作AC的垂直平分线l,交AB于E,交AC于F;
②在EF上截取;
③连接BD、CD,得.
请问,若按上述作法,裁得的型部件是否符合要求?请证明你的结论.
图1 图2 图3
(第26题图)
2024年陕西省初中学业水平考试信心提升卷
数学试卷参考答案
一、选择题(共8小题,每小题3分,计24分.每小题只有一个选项是符合题意的)
1. D 2. B 3. B 4. C 5. D 6. A 7. C 8. A
二、填空题(共5小题,每小题3分,计15分)
9. -3 10. 45 11. (其他形式正确也可) 12. <
13. 【解析】根据题意可得点P在矩形内以B为圆心,4为半径的圆弧上运动,在线段BC上取一点M,使得,连接MP、AM,于是有,根据相似三角形的判定可得,则,即,∴.当且仅当A、P、M三点共线时等号成立,利用勾股定理求出AM,即可求解.
三、解答题(共13小题,计81分.解答应写出过程)
14. 解:解得:,……(2分)
解得:,……(3分)
∴不等式组的解集为,……(4分)
∴不等式组的整数解是:-1,0. ……(5分)
15. 解:原式……(3分)
.……(5分)
16. 解:去分母,得,……(2分)
解得:,……(4分)
检验:当时,,
∴是原方程的根.……(5分)
17. 解:如图,点D即为所求.……(5分)
注:①答案中线条为实线或虚线均不扣分;②没有写出结论不扣分;③作法不唯一.
18. 证明:在矩形BCEF中,,……(1分)
∴,
∵O是边EF的中点,∴,……(2分)
在和中,,,,
∴.……(4分)
∴,即O是AB的中点.……(5分)
19. 解:(1)(或平行).……(2分)
(2)如图所示.……(5分)
20. 解:如图,过D作于P,交EF于N,
则,,
,,……(1分)
由题意得,,,
∴,……(3分)
∴,即,
∴,……(4分)
∴,
答:该塔的高AB为38米.……(5分)
注:算出,没有单位,没有答语不扣分.
21. 解:(1)0.4.……(2分)
(2)画树状图如下:……(4分)
由图知,一共有8种等可能的情况,其中所得数字之和大于3的有3种,
∴他获得玩偶的概率是.……(6分)
注:①在(2)中如果求出的概率正确,但没有列表格或画树状图扣2分;求出概率正确,若列表或画树状图后没有就结果作出说明不扣分;②在(2)中若运用枚举法直接列举出8种等可能结果,只要结果正确,不扣分.
22. 解:(1)根据题意,得.……(1分)
当时,设,
由题意得:,解得,
∴.……(4分)
(2)当时,,……(5分)
,
∵,
∴在甲超市购买更划算.……(7分)
23. 解:(1)11.……(2分)
C(或)……(4分)
(2)(名).
∴估计成绩不低于90分的学生有280名.……(6分)
(3)所抽取学生中,A组的学生人数占所抽取学生人数的.……(7分)
注:①(2)中没有答语、不带单位均不扣分;②(2)中没有计算过程扣1分;③(3)中答案不唯一,合理即可.
24.(1)证明:∵点A是的中点,
∴,∴,……(1分)
∵AB是的直径,,
∴,……(2分)
∴,
∵,∴,
∵,∴,……(3分)
∴BP为的切线.……(4分)
(2)解:∵,
∴,,
∴,……(6分)
∴,
∵M为OA的中点,∴,
∵,∴,
∴.……(8分)
25. 解:(1)将、代入中,得
,解得,
∴抛物线L的表达式为.……(2分)
∴顶点.……(3分)
过点P作轴于点D,则,
∵,,,
∴,,
∴.……(4分)
(2)由题意知,四边形是面积为12的平行四边形,
当抛物线沿x轴平移时,可得点在x轴上,
由于,即要使的面积为12,只需,
∵点在y轴左侧,
∴抛物线L沿x轴向左平移3个单位长度可得抛物线,
此时,抛物线的表达式为;……(6分)
当抛物线沿y轴平移时,可得点在直线DP上,
由于,要使的面积为12,只需,
∴抛物线L沿y轴向上或向下平移4个单位长度可得抛物线,
此时,抛物线的表达式为或.
综上,抛物线的表达式为或或.……(8分)
注:(2)中抛物线表达式为其他形式正确均可.
26. 解:(1)45.……(1分)
(2)证明:如图2,过点E作于M,于N.
∵四边形ABCD是正方形,
∴,,……(2分)
∵于M,于N,
∴,
∵,
∴四边形ANEM是矩形,……(3分)
∵,
∴,
∴,
∵,
∴,……(4分)
∴,
∵四边形DEFG是矩形,
∴四边形DEFG是正方形.……(5分)
图2
(3)如图3,过点A作于点G,过点D作于点M,
作于点N,连接AD,
∵EF是线段AC的垂直平分线,,
∴,,∴,
∵,,
∴点G为BC的中点,∴,
∴,
∵,,,∴,
∴四边形DNGM为矩形,……(7分)
∴,∴.
在和中,,,,
∴,……(8分)
∴,,
∴四边形DNGM为正方形,……(9分)
∴,
设,则,
∴,即,
解得,∴,
∴,
∴是等腰直角三角形,且,即.
故裁得的型部件符合要求.……(10分)
图3
同课章节目录
