六年级下册数学人教版数学思考课件(共27张PPT)
文档属性
| 名称 | 六年级下册数学人教版数学思考课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-20 09:10:37 | ||
图片预览






文档简介
(共27张PPT)
整理和复习
6
优翼
4. 数学思考
第1课时 数学思考(1)
一
复习导入
一、按规律填数。
① 1、4、9、( )、( )、( )。
② 2、5、11、23、47、( )、( )。
16
25
36
95
191
请同学们在纸上任意点上6个点,并将它们每两点连成一条线,再数一数,看看连成了多少条线段,那8个点呢?10个点呢?
一
一
复习导入
1
2
1
3
2
3
4
3
6
5
4
10
6
5
15
7
6
21
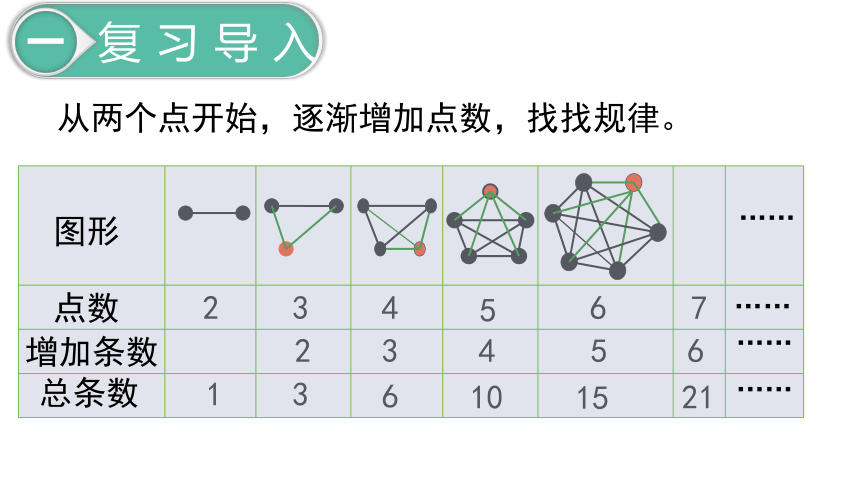
图形
点数
增加条数
总条数
……
……
……
……
一
复习导入
从两个点开始,逐渐增加点数,找找规律。
C
D
A
B
F
E
一
复习导入
点数 增加条数 总条数
2 1
3 2 1+2=3(条)
4 3 1+2+3=6(条)
5 4 1+2+3+4=10(条)
6 5 1+2+3+4+5=15(条)
规律变化如下:
一
复习导入
总条数=1 + 2 + 3 + 4 + 5 + 6 + …… +(点数-1)
点数×增加条数÷2
=
=
n×(n-1)÷2
n(n≥2)能连成n×(n-1)÷2条线段
二
强化训练
1.体育课上,10个同学比赛扳手腕,每两位同学比赛一次,请同学们帮忙算算,他们一共比了多少场?
答:一共比了45场。
10×(10 - 1)÷2=45(场)
二
强化训练
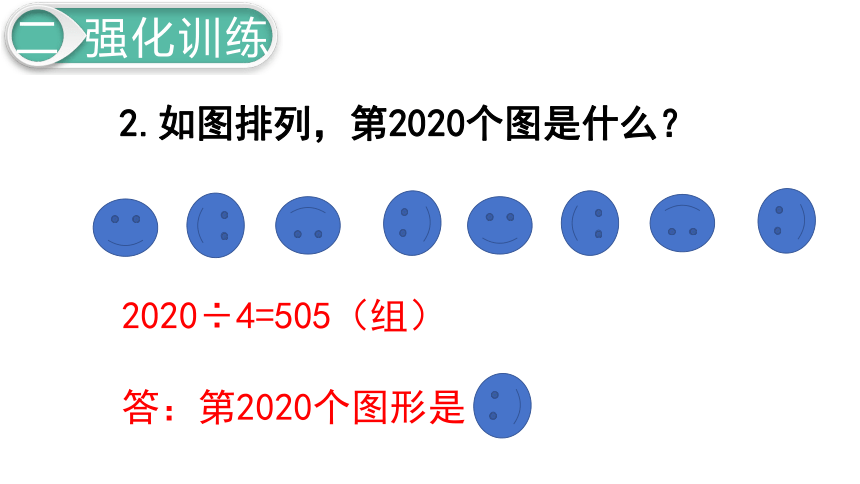
2.如图排列,第2020个图是什么?
2020÷4=505(组)
答:第2020个图形是
二
强化训练
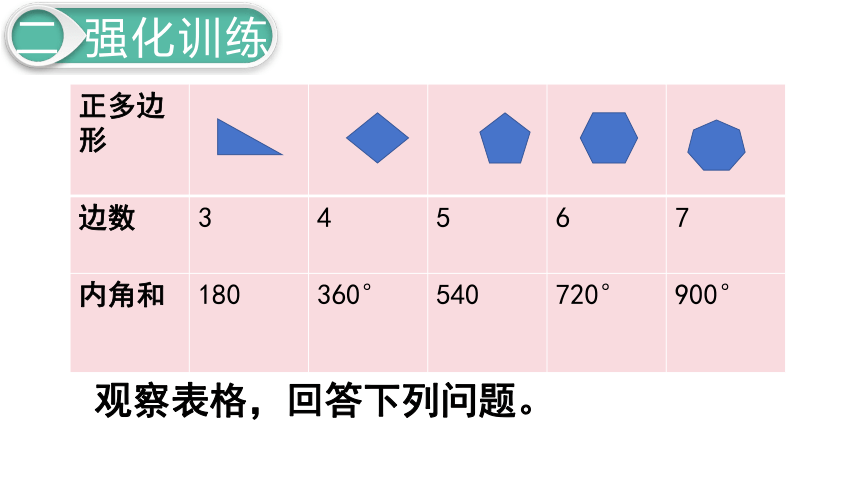
正多边形
边数 3 4 5 6 7
内角和 180 360° 540 720° 900°
观察表格,回答下列问题。
1.正多边形内角和与它的边数有什么关系?
2.一个正九边形的内角和是多少度?
多边形内角和=
180 ×
( n - 2 )
180
×
(9-2) = 1260°
二
强化训练
整理和复习
6
优翼
4. 数学思考
第2课时 数学思考(2)
一
复习导入
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的
列表法:用数字“1”表示到会,用数字“0”表示没到会。
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
2.
从第一次看出,A只可能和D、E、F同班;
从第二次判断,A只可能和D、E同班;
从第三次确定,A只可能和D同班。
同理:从第一次看出B可能和E、F同班,从第二次可以看出B和F同班,从而可知C和E同班。
一
复习导入
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
一
复习导入
排除法
从A考虑,由第一次和第三次到会情况,可知A不和B、C、E、F同班,所以A和D同班;
从B考虑,由第一次和第二次到会情况,可知B不和A、C、D、E同班,所以B和F同班;从而可知C和E同班。
二
强化训练
二
强化训练
二
强化训练
二
强化训练
5.六(1)班有男同学21人,女同学24人,如果从中任选一人去领奖,有多少种不同的选法?如果从中任选男、女同学各一人去参加座谈会,有多少种不同的选法?
任选一人:21+24=45(种)
各选一人:21×24=504(种)
答:任选一人有45种选法,男女各选一人
有504种选法。
整理和复习
6
优翼
4. 数学思考
第3课时 数学思考(3)
一
复习回顾
△、□、○、☆、◎各代表一个数。
(1)已知△+□=24, △=□+□+□。求△和□的值。
已知△+□=24,△=□+□+□,可得□+□+□+□=24,即4×□=24,所以□=6。△=□+□+□=18。
一个△等于三个□的和。
把△+□=24中的△换成□+□+□,这叫等量代换。
3
(2)已知○+☆=160, ◎+☆=160。○是否等于◎?
已知○+☆=160,◎+☆=160。根据等式的性质,等式两边都减去☆,可以推出,○=160 - ☆,◎=160-☆。
因为☆代表同一个数,所以○=◎。
两个等式
里都有☆。
可以利用等
式的性质。
一
复习回顾
什么是平角?平角与直线有什么区别?如右图,两条直线相交于点O。
(1)每相邻两个角可以组成一个平
角,一共能组成几个平角?
想:平角的两边在一条直线上。
∠1和∠2,∠2和∠3,∠3和∠4,
∠4和∠1,一共能组成4个平角。
一
复习回顾
4
(2)你能推出∠1=∠3吗?
想:∠1和∠2,∠2和∠3,都能组成平角。
根据第(1)题的结论,可以得到∠1+∠2=180°,∠2+∠3=180°
根据等式的性质,等式的两边都减去∠2,可以得到
∠1=180°-∠2°,∠3=180-∠2°。
因为180-∠2°=180-∠2°,所以∠1=∠3。
那接下来怎么办呢?
把∠1和∠2, ∠2和∠3的关系用等式表示出来。
一
复习回顾
王阿姨、刘阿姨、丁叔叔、李叔叔分别是工人、教师、军人。王阿姨是教师;丁叔叔不是工人;只有刘阿姨和李叔叔的职业相同。
请问:他们的职业各是什么?
问题:你想用什么方法解决这个问题?
二
巩固练习
二
巩固练习
列表是解决复杂问题的好方法。
王阿姨 刘阿姨 丁叔叔 李叔叔
工人
教师
军人
×
×
√
√
√
√
二
巩固练习
二
巩固练习
整理和复习
6
优翼
4. 数学思考
第1课时 数学思考(1)
一
复习导入
一、按规律填数。
① 1、4、9、( )、( )、( )。
② 2、5、11、23、47、( )、( )。
16
25
36
95
191
请同学们在纸上任意点上6个点,并将它们每两点连成一条线,再数一数,看看连成了多少条线段,那8个点呢?10个点呢?
一
一
复习导入
1
2
1
3
2
3
4
3
6
5
4
10
6
5
15
7
6
21
图形
点数
增加条数
总条数
……
……
……
……
一
复习导入
从两个点开始,逐渐增加点数,找找规律。
C
D
A
B
F
E
一
复习导入
点数 增加条数 总条数
2 1
3 2 1+2=3(条)
4 3 1+2+3=6(条)
5 4 1+2+3+4=10(条)
6 5 1+2+3+4+5=15(条)
规律变化如下:
一
复习导入
总条数=1 + 2 + 3 + 4 + 5 + 6 + …… +(点数-1)
点数×增加条数÷2
=
=
n×(n-1)÷2
n(n≥2)能连成n×(n-1)÷2条线段
二
强化训练
1.体育课上,10个同学比赛扳手腕,每两位同学比赛一次,请同学们帮忙算算,他们一共比了多少场?
答:一共比了45场。
10×(10 - 1)÷2=45(场)
二
强化训练
2.如图排列,第2020个图是什么?
2020÷4=505(组)
答:第2020个图形是
二
强化训练
正多边形
边数 3 4 5 6 7
内角和 180 360° 540 720° 900°
观察表格,回答下列问题。
1.正多边形内角和与它的边数有什么关系?
2.一个正九边形的内角和是多少度?
多边形内角和=
180 ×
( n - 2 )
180
×
(9-2) = 1260°
二
强化训练
整理和复习
6
优翼
4. 数学思考
第2课时 数学思考(2)
一
复习导入
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的
列表法:用数字“1”表示到会,用数字“0”表示没到会。
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
2.
从第一次看出,A只可能和D、E、F同班;
从第二次判断,A只可能和D、E同班;
从第三次确定,A只可能和D同班。
同理:从第一次看出B可能和E、F同班,从第二次可以看出B和F同班,从而可知C和E同班。
一
复习导入
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
一
复习导入
排除法
从A考虑,由第一次和第三次到会情况,可知A不和B、C、E、F同班,所以A和D同班;
从B考虑,由第一次和第二次到会情况,可知B不和A、C、D、E同班,所以B和F同班;从而可知C和E同班。
二
强化训练
二
强化训练
二
强化训练
二
强化训练
5.六(1)班有男同学21人,女同学24人,如果从中任选一人去领奖,有多少种不同的选法?如果从中任选男、女同学各一人去参加座谈会,有多少种不同的选法?
任选一人:21+24=45(种)
各选一人:21×24=504(种)
答:任选一人有45种选法,男女各选一人
有504种选法。
整理和复习
6
优翼
4. 数学思考
第3课时 数学思考(3)
一
复习回顾
△、□、○、☆、◎各代表一个数。
(1)已知△+□=24, △=□+□+□。求△和□的值。
已知△+□=24,△=□+□+□,可得□+□+□+□=24,即4×□=24,所以□=6。△=□+□+□=18。
一个△等于三个□的和。
把△+□=24中的△换成□+□+□,这叫等量代换。
3
(2)已知○+☆=160, ◎+☆=160。○是否等于◎?
已知○+☆=160,◎+☆=160。根据等式的性质,等式两边都减去☆,可以推出,○=160 - ☆,◎=160-☆。
因为☆代表同一个数,所以○=◎。
两个等式
里都有☆。
可以利用等
式的性质。
一
复习回顾
什么是平角?平角与直线有什么区别?如右图,两条直线相交于点O。
(1)每相邻两个角可以组成一个平
角,一共能组成几个平角?
想:平角的两边在一条直线上。
∠1和∠2,∠2和∠3,∠3和∠4,
∠4和∠1,一共能组成4个平角。
一
复习回顾
4
(2)你能推出∠1=∠3吗?
想:∠1和∠2,∠2和∠3,都能组成平角。
根据第(1)题的结论,可以得到∠1+∠2=180°,∠2+∠3=180°
根据等式的性质,等式的两边都减去∠2,可以得到
∠1=180°-∠2°,∠3=180-∠2°。
因为180-∠2°=180-∠2°,所以∠1=∠3。
那接下来怎么办呢?
把∠1和∠2, ∠2和∠3的关系用等式表示出来。
一
复习回顾
王阿姨、刘阿姨、丁叔叔、李叔叔分别是工人、教师、军人。王阿姨是教师;丁叔叔不是工人;只有刘阿姨和李叔叔的职业相同。
请问:他们的职业各是什么?
问题:你想用什么方法解决这个问题?
二
巩固练习
二
巩固练习
列表是解决复杂问题的好方法。
王阿姨 刘阿姨 丁叔叔 李叔叔
工人
教师
军人
×
×
√
√
√
√
二
巩固练习
二
巩固练习
