数学人教A版(2019)必修第二册8.5.1直线与直线平行 课件(共22张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册8.5.1直线与直线平行 课件(共22张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-20 21:25:21 | ||
图片预览








文档简介
(共22张PPT)
人教A版2019必修第二册
第 八 章 立体几何初步
8.5.1 直线与直线平行
1.掌握基本事实4和等角定理.
2.能用基本事实4解决一些简单的相关问题.
3.通过对基本事实4和等角定理的学习,培养直观想象、逻辑推理的数学素养.
教学目标
PART.01
情境引入
温故知新
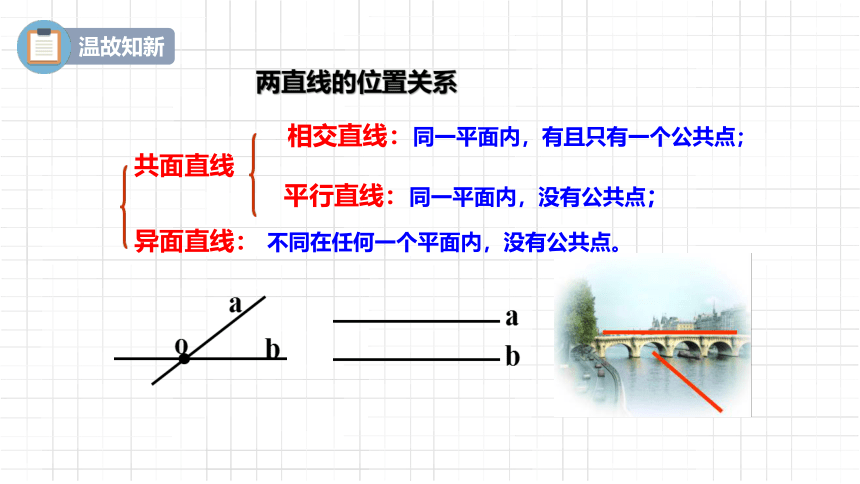
两直线的位置关系
相交直线:同一平面内,有且只有一个公共点;
共面直线
平行直线:同一平面内,没有公共点;
异面直线: 不同在任何一个平面内,没有公共点。
情境导入
立交桥是伴随高速公路应运而生的.城市的立交桥不仅大大方便了交通,而且成为城市建设的美丽风景,城市交通开始从平地走向立体.阅读教材,结合上述情境回答下列问题:
问题:若把图中的立交桥抽象成一直线,它们是否在同一平面内 它们有何特征
不共面.不相交也不平行.
问题提出
在平面几何的学习中,我们研究过两条直线的位置关系,重点研究了两条直线平行,得到了这种特殊位置关系的性质,以及判定两条直线平行的定理.
类似地,空间中直线、平面间的平行关系在生产和生活中有着广泛的应用,也是我们要重点研究的内容.
本节我们研究空间中直线、平面的平行关系,重点研究这些平行关系的判定和性质.
PART.02
基本事实4
概念讲解
在同一平面内,若a∥b且b∥c,则a∥c,即平面直线的平行具有传递性。
思考:在空间中,是否也有类似的结论
如图,在长方体中,,.那与平行吗?
从右图中可以发现, // .
概念讲解
问题:空间中的平行都具有传递性,那么你还能举出其他例子吗?
活动:将一张长方形的纸,对折2次后打开,如图所示,观察这些折痕有怎样的位置关系? 你能概括这个基本事实吗?
基本事实4 :平行于同一条直线的两条直线互相平行。
概念讲解
符号语言
简记为:空间中两直线平行的传递性
公理作用
判断空间两条直线平行的依据。
基本事实4
平行于同一条直线的两条直线平行(平行公理)
图形语言
概念讲解
例1. 如图,空间四边形中,分别是边,,的中点.
求证:四边形是平行四边形.
证明:连接∵是的中位线,
∴,且.
同理,且.
∴平行且相等.
∴四边形是平行四边形.
追问:在本例中,如果再加上条件,那么四边形是什么图形?
菱形
概念讲解
练习:如图所示,在正方体ABCD-A'B'C'D'中,若M,N分别是A′D′,C′D′的中点,
求证:四边形ACNM是梯形.
归纳小结
证明空间中两条直线平行的方法
(1)利用平面几何的知识(三角形与梯形的中位线、平行四边形的性质、平行线分线段成比例定理等)来证明.
(2)利用基本事实4,即找到一条直线,使得∥,同时∥,由基本事实4得到∥
PART.04
等角定理
概念讲解
思考:在平面内,如果一个角的两边与另一个角的两边分别对应平行,那么这两个角相等或互补.在空间中,这一结论是否仍然成立呢?
与平面中的情况类似,当空间中两个角的两边分别对应平行时,这两个角有如图所示的两种位置.
概念讲解
证明:如图,分别在和的两边上截取,和,,
使得,.连接,, ,,
∵,且AD=∴四边形是平行四边形.
∴同理可证.
∴. ∴四边形是平行四边形.
∴. ∴.
∴.
分析:对于图(1),我们可以构造两个全等三角形,使和是它们的对应角,从而证明.
分析:对于图(2),显然,当的方向与上述情形相反时,与互补.
概念讲解
或
符号语言
公理作用
证明空间中两角相等
图形语言
等角定理
如果空间中两个角的两条边分别对应平行,那么这两个角相等或互补
概念讲解
概念讲解
练习2:如图,在正方形中,分别为棱的中点.
求证:(1)四边形为平行四边形;(2).
解:(1)∵为正方体,∴,且.
又为别为棱的中点,∴,且.
∴四边形为平行四边形.
∴且.
又且,∴且.
∴四边形为平行四边形.
概念讲解
(2)由(1)知四边形为平行四边形,
∴.
同理可得四边形为平行四边形.∴.
∵和方向相同,
∴.
PART.06
课堂小结
课堂小结
人教A版2019必修第二册
第 八 章 立体几何初步
8.5.1 直线与直线平行
1.掌握基本事实4和等角定理.
2.能用基本事实4解决一些简单的相关问题.
3.通过对基本事实4和等角定理的学习,培养直观想象、逻辑推理的数学素养.
教学目标
PART.01
情境引入
温故知新
两直线的位置关系
相交直线:同一平面内,有且只有一个公共点;
共面直线
平行直线:同一平面内,没有公共点;
异面直线: 不同在任何一个平面内,没有公共点。
情境导入
立交桥是伴随高速公路应运而生的.城市的立交桥不仅大大方便了交通,而且成为城市建设的美丽风景,城市交通开始从平地走向立体.阅读教材,结合上述情境回答下列问题:
问题:若把图中的立交桥抽象成一直线,它们是否在同一平面内 它们有何特征
不共面.不相交也不平行.
问题提出
在平面几何的学习中,我们研究过两条直线的位置关系,重点研究了两条直线平行,得到了这种特殊位置关系的性质,以及判定两条直线平行的定理.
类似地,空间中直线、平面间的平行关系在生产和生活中有着广泛的应用,也是我们要重点研究的内容.
本节我们研究空间中直线、平面的平行关系,重点研究这些平行关系的判定和性质.
PART.02
基本事实4
概念讲解
在同一平面内,若a∥b且b∥c,则a∥c,即平面直线的平行具有传递性。
思考:在空间中,是否也有类似的结论
如图,在长方体中,,.那与平行吗?
从右图中可以发现, // .
概念讲解
问题:空间中的平行都具有传递性,那么你还能举出其他例子吗?
活动:将一张长方形的纸,对折2次后打开,如图所示,观察这些折痕有怎样的位置关系? 你能概括这个基本事实吗?
基本事实4 :平行于同一条直线的两条直线互相平行。
概念讲解
符号语言
简记为:空间中两直线平行的传递性
公理作用
判断空间两条直线平行的依据。
基本事实4
平行于同一条直线的两条直线平行(平行公理)
图形语言
概念讲解
例1. 如图,空间四边形中,分别是边,,的中点.
求证:四边形是平行四边形.
证明:连接∵是的中位线,
∴,且.
同理,且.
∴平行且相等.
∴四边形是平行四边形.
追问:在本例中,如果再加上条件,那么四边形是什么图形?
菱形
概念讲解
练习:如图所示,在正方体ABCD-A'B'C'D'中,若M,N分别是A′D′,C′D′的中点,
求证:四边形ACNM是梯形.
归纳小结
证明空间中两条直线平行的方法
(1)利用平面几何的知识(三角形与梯形的中位线、平行四边形的性质、平行线分线段成比例定理等)来证明.
(2)利用基本事实4,即找到一条直线,使得∥,同时∥,由基本事实4得到∥
PART.04
等角定理
概念讲解
思考:在平面内,如果一个角的两边与另一个角的两边分别对应平行,那么这两个角相等或互补.在空间中,这一结论是否仍然成立呢?
与平面中的情况类似,当空间中两个角的两边分别对应平行时,这两个角有如图所示的两种位置.
概念讲解
证明:如图,分别在和的两边上截取,和,,
使得,.连接,, ,,
∵,且AD=∴四边形是平行四边形.
∴同理可证.
∴. ∴四边形是平行四边形.
∴. ∴.
∴.
分析:对于图(1),我们可以构造两个全等三角形,使和是它们的对应角,从而证明.
分析:对于图(2),显然,当的方向与上述情形相反时,与互补.
概念讲解
或
符号语言
公理作用
证明空间中两角相等
图形语言
等角定理
如果空间中两个角的两条边分别对应平行,那么这两个角相等或互补
概念讲解
概念讲解
练习2:如图,在正方形中,分别为棱的中点.
求证:(1)四边形为平行四边形;(2).
解:(1)∵为正方体,∴,且.
又为别为棱的中点,∴,且.
∴四边形为平行四边形.
∴且.
又且,∴且.
∴四边形为平行四边形.
概念讲解
(2)由(1)知四边形为平行四边形,
∴.
同理可得四边形为平行四边形.∴.
∵和方向相同,
∴.
PART.06
课堂小结
课堂小结
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
