7.1探索直线平行的条件 自主学习填空题专题训练(含解析) 苏科版七年级数学下册
文档属性
| 名称 | 7.1探索直线平行的条件 自主学习填空题专题训练(含解析) 苏科版七年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 279.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-20 00:00:00 | ||
图片预览



文档简介
苏科版七年级数学下册《7.1探索直线平行的条件》
自主学习填空题专题训练
1.已知a,b,c在同一平面内的三条直线,若,,则a c.
2.三条直线,则 ,理由是 .
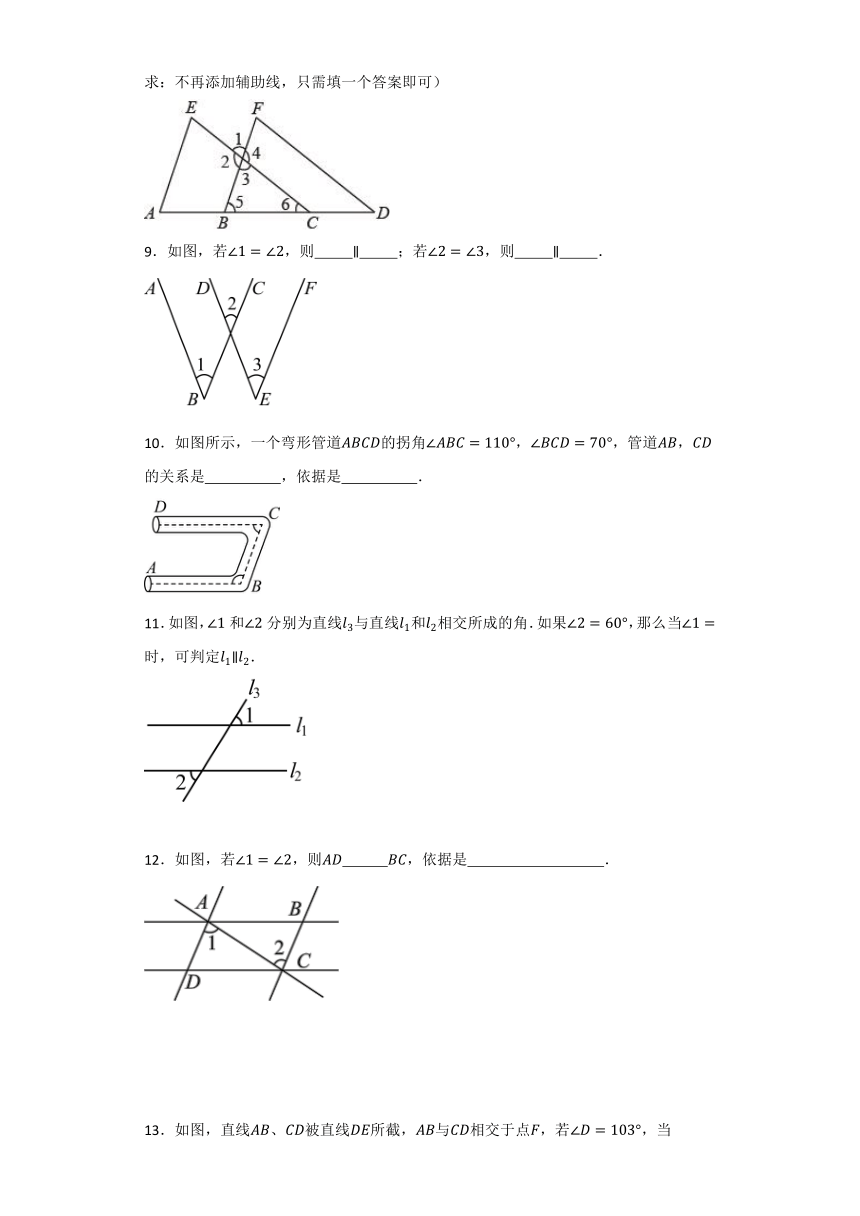
3.如图所示,直线与被直线所截得的内错角是 ;直线与被直线所截得的内错角是 ;的内错角是 .
AI
4.如图,直线L截直线a,b所得的同位角有 对;内错角有 对,它们是 ;同旁内角有 对,它们是 ;对顶角 对,它们是 .
5.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是 .
6.1.如图,如果,那么 .
7.如图,点在的延长线上,请添加一个恰当的条件 ,使.
8.如图,点A,B,C,D在同一条直线上,若满足条件 ,则有CE∥DF,理由是 .(要求:不再添加辅助线,只需填一个答案即可)
9.如图,若,则 ;若,则 .
10.如图所示,一个弯形管道的拐角,,管道,的关系是 ,依据是 .
11.如图,和分别为直线与直线和相交所成的角.如果,那么当 时,可判定.
12.如图,若,则 ,依据是 .
13.如图,直线、被直线所截,与相交于点,若,当 时,.
14.如图,点E在AC的延长线上,对于给出的四个条件:
①∠1=∠2;
②∠3=∠4;
③∠A=∠DCE;
④∠A+∠ABD=180°.
能判断AB∥CD的有 (填写序号).
15.(1)如果,那么________________,根据( )
(2)如果,那么________________,根据( )
(3)如果,那么________________,根据( )
16.如图,已知点A,B,C和点D,E,F分别在同一直线上,,那么可以最终推出 ∥ ,判定平行的理由是 .
17.如图,有下列说法:①若,则;②若,则;③若,则;④若,则.其中说法正确的有 个.
18.如图,,平分,则与的位置关系是 .
19.如图所示,已知∠1=56°,∠2=44°,∠3=80°,那么 ∥ ,判断依据是 .
20.将一块三角板ABC(∠BAC=90°,∠ABC=30°)按如图方式放置,使A,B两点分别落在直线m,n上,对于给出的五个条件:①∠1=25.5°,∠2=55°;②∠1+∠2=90°;③∠2=2∠1;④∠ACB=∠1+∠3;⑤∠ABC=∠2-∠1.能判断直线mn的有 .(填序号)
参考答案
1.解:∵,,
∴,
故答案为:.
2.解:∵直线,
∴(平行于同一条直线的两条直线平行).
即三条直线,则,理由是平行于同一条直线的两条直线平行.
故答案为:,平行于同一条直线的两条直线平行
3. 解:直线与被直线所截得的内错角是和;直线与被直线所截得的内错角是和;的内错角是和.
故答案为:和;和;和.
4. 解:直线l截直线a,b所得的同位角有4对,分别是与,与,与,与;
内错角有2对,它们是与∠8,与;
同旁内角有2对,它们是与,与;
对顶角有4对,它们是与,与,与,与.
故答案为:4;2;与,与;2;与,与;4;与,与,与,与
5.解:如图
由画图过程可知:
三角板沿着直线平移到三角板的位置得:
,
根据同位角相等,两直线平行得:,
故答案为:同位角相等,两直线平行.
6.解:∵,
∴,(内错角相等,两直线平行).
故答案为:;.
7.解:当时,;
当时,;
当时,.
故答案为:或或(任填一个即可).
8.解:若∠3=∠F,则CE∥DF,
理由是:同位角相等,两直线平行,
故答案为:∠3=∠F,同位角相等,两直线平行.(答案不唯一)
9. 解:∵,
∴,
∵,
∴,
故答案为:,,,.
10.解:∵,,
∴,
∴(同旁内角互补,两直线平行).
故答案为:,同旁内角互补,两直线平行.
11.解:当时,
解:∵,
∴,
∴,
∴,
故答案为.
12.解:若,,依据是内错角相等,两直线平行.
故答案为:,内错角相等,两直线平行.
13.解:∵,
当时,;
∵,
∴,
故答案为:.
14.解:①根据内错角相等,两直线平行即可证得AB∥CD;
②根据内错角相等,两直线平行即可证得BD∥AC,不能证明AB∥CD;
③根据同位角相等,两直线平行即可证得AB∥CD;
④根据同旁内角互补,两直线平行即可证得BD∥AC,不能证明AB∥CD.
故答案为:①③.
15.解:(1)由图中可得和是同位角,根据同位角相等,两直线平行得到;
(2)由图中可得和是内错角,再根据内错角相等,两直线平行得到;
(3)由图中可得和是同旁内角且,再根据同旁内角互补,两直线平行得到.
16.解:∵,,
∴,
∴(同位角相等,两直线平行).
故答案为:;;同位角相等,两直线平行.
17.1
18.解:∵平分,
∴,
∵,
∴,
∴,
故答案为:平行.
19. 解:∵∠1+∠3+∠ABD=180°,∠1=56°,∠3=80°,
∴∠ABD=180°﹣56°﹣80°=44°,
∵∠2=44°,
∴∠2=∠ABD,
∴AB∥CD(内错角相等,两直线平行),
故答案为:AB;CD;内错角相等,两直线平行.
20.解:∵∠1=25.5°,∠2=55°,∠ABC=30°,
∴∠ABC+∠1=55.5°=55°=∠2,
∴mn,故①符合题意;
∵∠1+∠2=90°,∠ABC=30°,
∴∠1+∠ABC不一定等于∠2,
∴m和n不一定平行,故②不符合题意;
∵∠2=2∠1,∠ABC=30°,
∴∠1+∠ABC不一定等于∠2,
∴m和n不一定平行,故③不符合题意;
过点C作CEm,
∴∠3=∠4,
∵∠ACB=∠1+∠3,∠ACB=∠4+∠5,
∴∠1=∠5,
∴ECn,
∴mn,故④符合题意;
∵∠ABC=∠2-∠1,
∴∠2=∠ABC+∠1,
∴mn,故⑤符合题意;
故答案为:①④⑤.
自主学习填空题专题训练
1.已知a,b,c在同一平面内的三条直线,若,,则a c.
2.三条直线,则 ,理由是 .
3.如图所示,直线与被直线所截得的内错角是 ;直线与被直线所截得的内错角是 ;的内错角是 .
AI
4.如图,直线L截直线a,b所得的同位角有 对;内错角有 对,它们是 ;同旁内角有 对,它们是 ;对顶角 对,它们是 .
5.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是 .
6.1.如图,如果,那么 .
7.如图,点在的延长线上,请添加一个恰当的条件 ,使.
8.如图,点A,B,C,D在同一条直线上,若满足条件 ,则有CE∥DF,理由是 .(要求:不再添加辅助线,只需填一个答案即可)
9.如图,若,则 ;若,则 .
10.如图所示,一个弯形管道的拐角,,管道,的关系是 ,依据是 .
11.如图,和分别为直线与直线和相交所成的角.如果,那么当 时,可判定.
12.如图,若,则 ,依据是 .
13.如图,直线、被直线所截,与相交于点,若,当 时,.
14.如图,点E在AC的延长线上,对于给出的四个条件:
①∠1=∠2;
②∠3=∠4;
③∠A=∠DCE;
④∠A+∠ABD=180°.
能判断AB∥CD的有 (填写序号).
15.(1)如果,那么________________,根据( )
(2)如果,那么________________,根据( )
(3)如果,那么________________,根据( )
16.如图,已知点A,B,C和点D,E,F分别在同一直线上,,那么可以最终推出 ∥ ,判定平行的理由是 .
17.如图,有下列说法:①若,则;②若,则;③若,则;④若,则.其中说法正确的有 个.
18.如图,,平分,则与的位置关系是 .
19.如图所示,已知∠1=56°,∠2=44°,∠3=80°,那么 ∥ ,判断依据是 .
20.将一块三角板ABC(∠BAC=90°,∠ABC=30°)按如图方式放置,使A,B两点分别落在直线m,n上,对于给出的五个条件:①∠1=25.5°,∠2=55°;②∠1+∠2=90°;③∠2=2∠1;④∠ACB=∠1+∠3;⑤∠ABC=∠2-∠1.能判断直线mn的有 .(填序号)
参考答案
1.解:∵,,
∴,
故答案为:.
2.解:∵直线,
∴(平行于同一条直线的两条直线平行).
即三条直线,则,理由是平行于同一条直线的两条直线平行.
故答案为:,平行于同一条直线的两条直线平行
3. 解:直线与被直线所截得的内错角是和;直线与被直线所截得的内错角是和;的内错角是和.
故答案为:和;和;和.
4. 解:直线l截直线a,b所得的同位角有4对,分别是与,与,与,与;
内错角有2对,它们是与∠8,与;
同旁内角有2对,它们是与,与;
对顶角有4对,它们是与,与,与,与.
故答案为:4;2;与,与;2;与,与;4;与,与,与,与
5.解:如图
由画图过程可知:
三角板沿着直线平移到三角板的位置得:
,
根据同位角相等,两直线平行得:,
故答案为:同位角相等,两直线平行.
6.解:∵,
∴,(内错角相等,两直线平行).
故答案为:;.
7.解:当时,;
当时,;
当时,.
故答案为:或或(任填一个即可).
8.解:若∠3=∠F,则CE∥DF,
理由是:同位角相等,两直线平行,
故答案为:∠3=∠F,同位角相等,两直线平行.(答案不唯一)
9. 解:∵,
∴,
∵,
∴,
故答案为:,,,.
10.解:∵,,
∴,
∴(同旁内角互补,两直线平行).
故答案为:,同旁内角互补,两直线平行.
11.解:当时,
解:∵,
∴,
∴,
∴,
故答案为.
12.解:若,,依据是内错角相等,两直线平行.
故答案为:,内错角相等,两直线平行.
13.解:∵,
当时,;
∵,
∴,
故答案为:.
14.解:①根据内错角相等,两直线平行即可证得AB∥CD;
②根据内错角相等,两直线平行即可证得BD∥AC,不能证明AB∥CD;
③根据同位角相等,两直线平行即可证得AB∥CD;
④根据同旁内角互补,两直线平行即可证得BD∥AC,不能证明AB∥CD.
故答案为:①③.
15.解:(1)由图中可得和是同位角,根据同位角相等,两直线平行得到;
(2)由图中可得和是内错角,再根据内错角相等,两直线平行得到;
(3)由图中可得和是同旁内角且,再根据同旁内角互补,两直线平行得到.
16.解:∵,,
∴,
∴(同位角相等,两直线平行).
故答案为:;;同位角相等,两直线平行.
17.1
18.解:∵平分,
∴,
∵,
∴,
∴,
故答案为:平行.
19. 解:∵∠1+∠3+∠ABD=180°,∠1=56°,∠3=80°,
∴∠ABD=180°﹣56°﹣80°=44°,
∵∠2=44°,
∴∠2=∠ABD,
∴AB∥CD(内错角相等,两直线平行),
故答案为:AB;CD;内错角相等,两直线平行.
20.解:∵∠1=25.5°,∠2=55°,∠ABC=30°,
∴∠ABC+∠1=55.5°=55°=∠2,
∴mn,故①符合题意;
∵∠1+∠2=90°,∠ABC=30°,
∴∠1+∠ABC不一定等于∠2,
∴m和n不一定平行,故②不符合题意;
∵∠2=2∠1,∠ABC=30°,
∴∠1+∠ABC不一定等于∠2,
∴m和n不一定平行,故③不符合题意;
过点C作CEm,
∴∠3=∠4,
∵∠ACB=∠1+∠3,∠ACB=∠4+∠5,
∴∠1=∠5,
∴ECn,
∴mn,故④符合题意;
∵∠ABC=∠2-∠1,
∴∠2=∠ABC+∠1,
∴mn,故⑤符合题意;
故答案为:①④⑤.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
