7.2探索平行线的性质 同步训练(含解析) 苏科版七年级数学下册
文档属性
| 名称 | 7.2探索平行线的性质 同步训练(含解析) 苏科版七年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 598.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-20 00:00:00 | ||
图片预览



文档简介
7.2探索平行线的性质同步训练-苏科版七年级数学下册
一、选择题
1.如图,直线,将含有角的直角三角尺按如图所示的位置放置,若,那么的大小为( )
A. B. C. D.
2.如图,一条公路两次转弯后又回到与原来相同的方向,,那么的度数是( )
A. B. C. D.
3.如图,下列推理及所说理由正确的是( )
A.因为DE∥BC,所以∠1=∠C.理由:同位角相等,两直线平行
B.因为∠2=∠3,所以DE∥BC.理由:同位角相等,两直线平行
C.因为DE∥BC,所以∠2=∠3.理由:两直线平行,内错角相等
D.因为∠1=∠C,所以DE∥BC.理由:两直线平行,同位角相等
4.如图,是一块直角三角板,其中,直尺的一边经过顶点,若,则的度数为( )
A. B. C. D.
5.在数学拓展课《折叠的奥秘》中,老师提出一个问题:如图,有一条宽度相等的长方形纸带,将纸条沿折叠一下,若,则的度数为( )
A. B. C. D.
6.如图,点在直线上,,,若,则的度数是( )
A. B. C. D.
7.绿色出行,健康你我.“美团”为了方便市民出行,提供了共享单车服务,图1是“美团”共享单车放在水平地面的实物图,图2是其示意图,其中都与地面平行,与也平行,若,则的度数为( )
A. B. C. D.
8.如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠CDO=50°,则下列结论:①OG⊥AB;②OF平分∠BOD;③∠AOE=65°;④∠GOE=∠DOF,其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
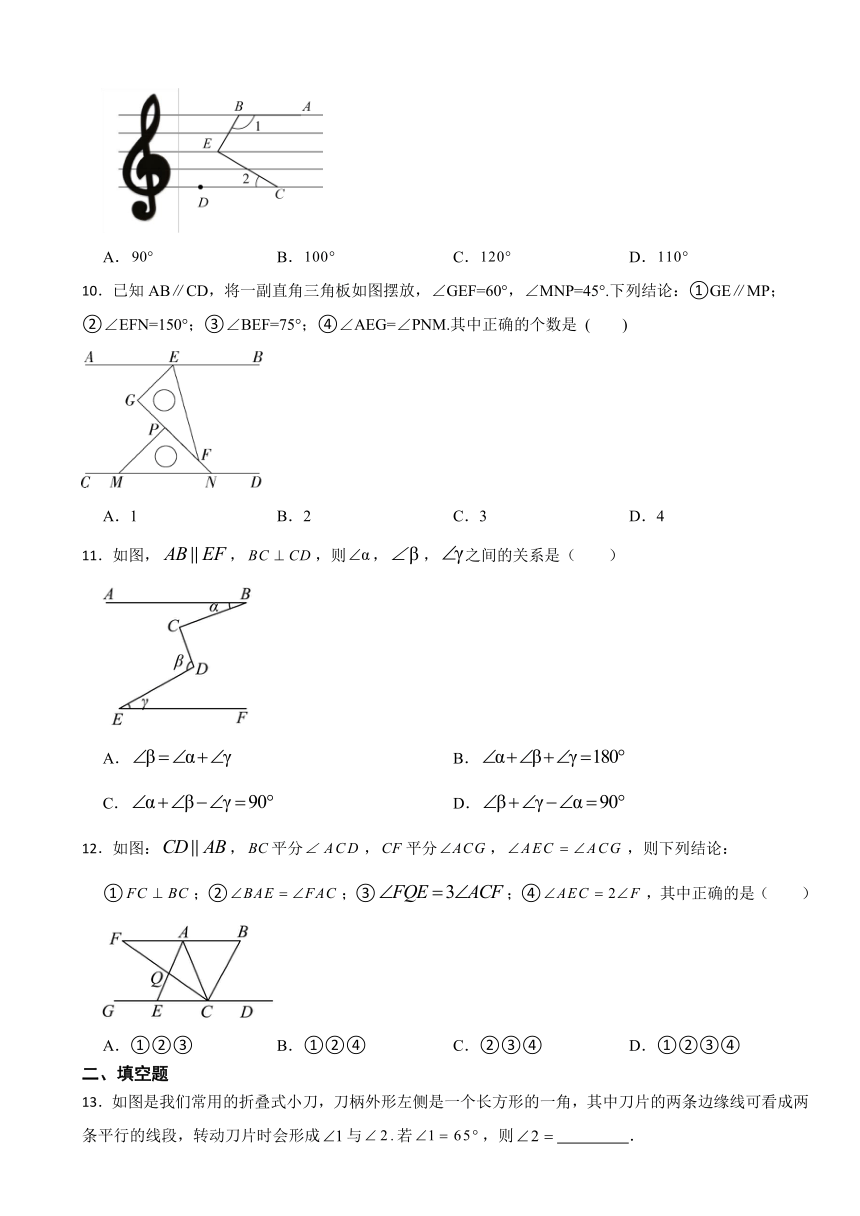
9.五线谱是一种记谱法,通过五根等距离的平行线上标以不同的音符构成旋律,如图,和是五线谱上的两条线段,点E在,之间的一条平行线上,若,,则的度数是( )
A. B. C. D.
10.已知AB∥CD,将一副直角三角板如图摆放,∠GEF=60°,∠MNP=45°.下列结论:①GE∥MP;②∠EFN=150°;③∠BEF=75°;④∠AEG=∠PNM.其中正确的个数是 ( )
A.1 B.2 C.3 D.4
11.如图,,,则,,之间的关系是( )
A. B.
C. D.
12.如图:,平分,平分,,则下列结论:
①;②;③;④,其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
二、填空题
13.如图是我们常用的折叠式小刀,刀柄外形左侧是一个长方形的一角,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成与若,则 .
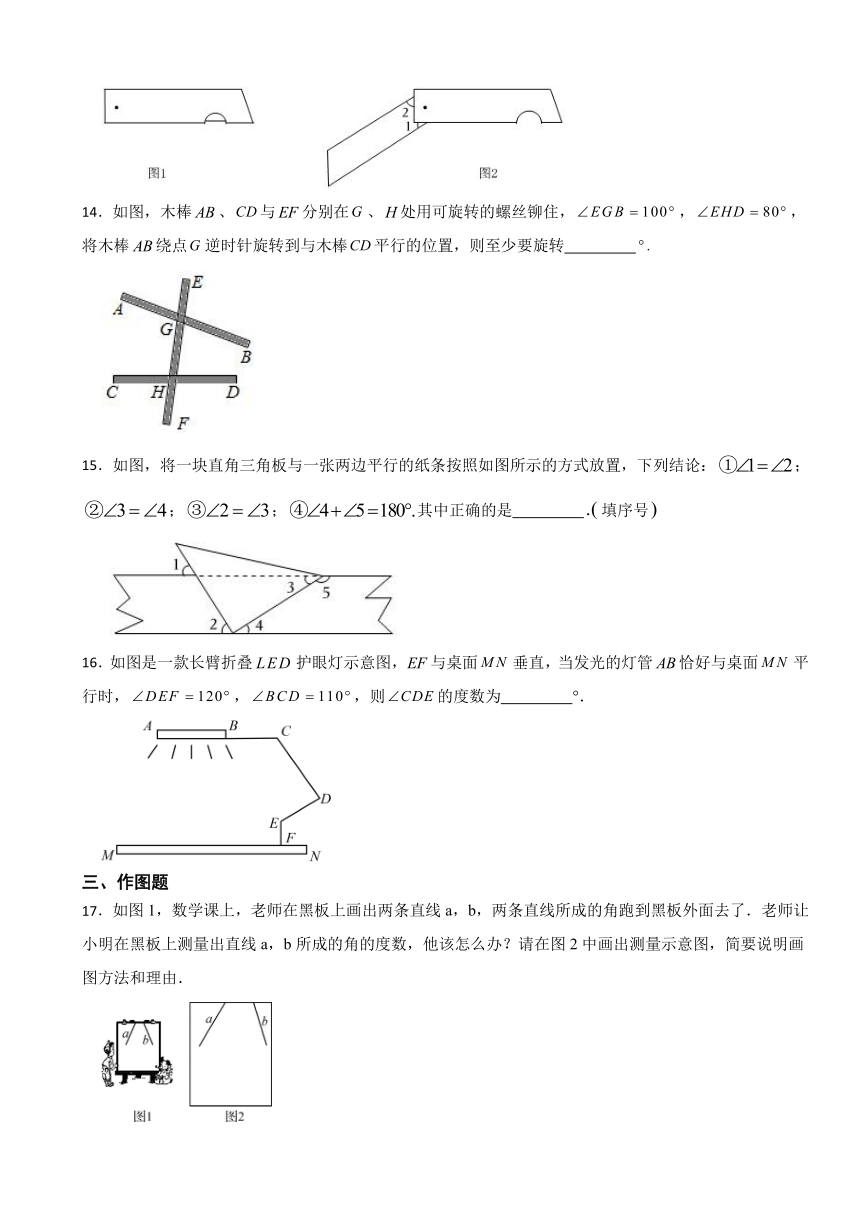
14.如图,木棒、与分别在、处用可旋转的螺丝铆住,,,将木棒绕点逆时针旋转到与木棒平行的位置,则至少要旋转
15.如图,将一块直角三角板与一张两边平行的纸条按照如图所示的方式放置,下列结论:;;;其中正确的是 填序号
16.如图是一款长臂折叠护眼灯示意图,与桌面垂直,当发光的灯管恰好与桌面平行时,,,则的度数为 °.
三、作图题
17.如图1,数学课上,老师在黑板上画出两条直线a,b,两条直线所成的角跑到黑板外面去了.老师让小明在黑板上测量出直线a,b所成的角的度数,他该怎么办?请在图2中画出测量示意图,简要说明画图方法和理由.
四、解答题
18.如图,直线 , 于 点,若 ,求 的度数.
19.如图,,交于点F,,垂足为E.
(1)若,求的度数;
(2)直接写出图中与互余的所有角.
20.如图,已知,.
(1)试问与相等吗?请说明理由;
(2)若,,求的度数.
答案解析部分
1.【答案】C
【解析】解:如图,
∵∠3=60°-∠1=60°-15°=45°,a∥b,
∴∠4=∠3=45°,
∴∠2=180°-∠3-∠4=180°-90°-45°=45°.
故答案为:C.
2.【答案】D
3.【答案】C
【解析】解:A、理由应该是两直线平行,同位角相等,故此选项错误;
B、理由应该是:内错角相等,两直线平行,故此选项错误;
C、此选项推理过程及说理都是正确的,符合题意;
D、理由应该是:同位角相等,两直线平行,故此选项错误.
故答案为:C.
4.【答案】B
【解析】解:∵ , ,
∴
∴
故答案为:B.
5.【答案】A
【解析】解:如图:
根据折叠的性质可得:∠3=∠4,
∵a//b,
∴∠1=∠3+∠4=2∠3=130°,
∴∠3=65°,
∵∠2+∠3=180°,
∴∠2=180°-∠3=180°-65°=115°,
故答案为:A .
6.【答案】A
【解析】解:∵EO⊥OF,
∴∠EOF=90°,
又∵∠BOF=55°,
∴∠EOB=90°-55°=35°,
∵AB//CD,
∴∠EOB+∠DEO=180°,
∴∠DEO=145°,
故答案为:A.
7.【答案】C
8.【答案】D
【解析】解:∵AB//CD,OG//CD,
∴OG⊥AB,
∴结论①正确;
∵AB//CD,
∴∠BOD=∠CDO=50°,
∴∠AOD=180°-∠BOD=130°,
∵OE平分∠AOD,
∴,
∴结论③正确;
∵OG⊥CD,
∴∠GOA=∠DGO=90°,
∴∠GOD=40°,∠GOE=90°-∠AOE=25°,
∴∠EOG+∠GOD=25°+40°=65°,
∵OE⊥OF,∠FOE=90°,
∴∠DOF=25°,
∴∠BOF=∠DOF,
∴OF平分∠BOD,∠GOE=∠DOF,
∴结论②④正确;
综上所述:正确的有4个,
故答案为:D.
9.【答案】A
【解析】解:∵AB∥EF,EF∥CD, ,
∴∠BEF=180°-∠1=60°,∠FEC=∠2=30°,
∴∠BEC=∠BEF+∠FEC=60°+30°=90°;
故答案为:A.
10.【答案】D
【解析】解:①由题意可得:∠G=∠MPN=90°,
∴∠G=∠MPG=90°,
∴GE//MP,
∴结论①正确;
②由题意可得:∠EFG=30°,
∴EFN=180°-∠EFG=150°,
∴结论②正确;
③过点F作FH//AB,如下图所示:
∵AB//CD, FH//AB,
∴∠BEF +∠EFH=180°,FH//CD,
∴∠HFN=MNP=45°,
∴∠EFH=∠EFN-∠HFN=105°,
∴∠BEF=180°-∠EFH=75°,
∴结论③正确;
∵∠GEF=60°,∠BEF=75°,
∴∠AEG=180°-∠GEF-∠BEF=45°,
∵∠MNP=45°,
∴∠AEG=∠PNM,
∴结论④正确,
综上所述:正确的个数是4个,
故答案为:D.
11.【答案】C
【解析】解:如图,过点C作CG∥AB,过点D作DH∥EF,如图,
∴∠BCG=α,∠EDH=γ,
∵BC⊥CD,∠CDE=β,
∴∠CDH=β-γ,∠GCD=90°-α,
∵AB∥EF,
∴AB∥CG∥DH∥EF,
∴∠GCD=∠CDH,
∴β-γ=90°-α,
∴α+β-γ=90°.
故答案为:C.
12.【答案】D
【解析】 ①由已知角平分线的条件可得∠FCA=∠ACG,∠ACB=∠ACD, ∴∠FCB= (∠ACG+∠ACD)= 180°=90°∴①正确;② 由AE=AC知∠AEC=∠ACE(等边对等角),又∠BAE= 180°-∠AEC(两直线平行同旁内角互补)同理 ∠FAC= 180°-∠ACE ∴∠BAE= ∠FAC(等角的补角相等) ②正确;③由题意知∠AEC=∠ACE=2∠ACF=2∠FCE ∴∠AQC=∠AEC+∠FCE(三角形的一个外角等于不相邻的两个内角和) ∴∠FQE=∠AQC=∠AEC+∠FCE=2∠ACF+∠ACF=3∠ACF (等量代换) ③正确;④由题意知∠AEC=∠ACE 且∠ACE=2∠FCE又∠F=∠FCE ∴∠AEC=2∠FCE=2∠F 故④正确
13.【答案】
【解析】解:过AB做A,B延长线交CD于E,如下图2
∵∠2=,刀柄左侧是一个长方形的一角
∴∠BED==
又∵AF//CD
∴∠1=∠BED=
故答案为:.
14.【答案】20
【解析】解:当∠EGB=∠EHD时,AB//CD.
∵∠EGB=100°,∠EHD=80°
∴将木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转100°-80°=20°.
故答案为:20.
15.【答案】
【解析】解:;正确,两直线平行,同位角相等
;正确,两直线平行,内错角相等
;不正确,在前两个结论正确的基础上,
正确,两直线平行,同旁内角互补。
故答案为:
16.【答案】100
【解析】解:过点E作GE∥MN,过点D作HD∥CA,如图所示:
∴∠FEG+∠NFE=180°,∠HDC+∠DCA=180°,
∵,,
∴∠HDC=70°,∠NFE=∠FEG=90°,∠GED=30°,
∵BA∥MN,
∴EG∥HD,
∴∠EDH=30°,
∴,
故答案为:100
17.【答案】解:如图,过点O作直线c∥a,测量出∠1的度数即可解决问题.
理由:由作图可知:a∥c,
∴∠1就等于直线a、b相交形成的角(两直线平行,同位角相等).
18.【答案】解:∵AB∥CD,
∴∠NMB=∠MNC=60°,
又∵MN⊥CE,
∴∠EMN=90°,
∴∠EMB=90°-∠NMB=90°-60°=30°.
19.【答案】(1)解:∵,
∴,
∵,
∴,
∴,
∴;
(2)
【解析】解:(2)解:∵,,
∴,,
即都与互余.
20.【答案】(1)解:与相等,理由如下:
∵,
,
,
同角的补角相等,
∴(内错角相等,两直线平行,
两直线平行,同位角相等
(2)解:∵,
,
,,
,即,
,,
,
即.
一、选择题
1.如图,直线,将含有角的直角三角尺按如图所示的位置放置,若,那么的大小为( )
A. B. C. D.
2.如图,一条公路两次转弯后又回到与原来相同的方向,,那么的度数是( )
A. B. C. D.
3.如图,下列推理及所说理由正确的是( )
A.因为DE∥BC,所以∠1=∠C.理由:同位角相等,两直线平行
B.因为∠2=∠3,所以DE∥BC.理由:同位角相等,两直线平行
C.因为DE∥BC,所以∠2=∠3.理由:两直线平行,内错角相等
D.因为∠1=∠C,所以DE∥BC.理由:两直线平行,同位角相等
4.如图,是一块直角三角板,其中,直尺的一边经过顶点,若,则的度数为( )
A. B. C. D.
5.在数学拓展课《折叠的奥秘》中,老师提出一个问题:如图,有一条宽度相等的长方形纸带,将纸条沿折叠一下,若,则的度数为( )
A. B. C. D.
6.如图,点在直线上,,,若,则的度数是( )
A. B. C. D.
7.绿色出行,健康你我.“美团”为了方便市民出行,提供了共享单车服务,图1是“美团”共享单车放在水平地面的实物图,图2是其示意图,其中都与地面平行,与也平行,若,则的度数为( )
A. B. C. D.
8.如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠CDO=50°,则下列结论:①OG⊥AB;②OF平分∠BOD;③∠AOE=65°;④∠GOE=∠DOF,其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
9.五线谱是一种记谱法,通过五根等距离的平行线上标以不同的音符构成旋律,如图,和是五线谱上的两条线段,点E在,之间的一条平行线上,若,,则的度数是( )
A. B. C. D.
10.已知AB∥CD,将一副直角三角板如图摆放,∠GEF=60°,∠MNP=45°.下列结论:①GE∥MP;②∠EFN=150°;③∠BEF=75°;④∠AEG=∠PNM.其中正确的个数是 ( )
A.1 B.2 C.3 D.4
11.如图,,,则,,之间的关系是( )
A. B.
C. D.
12.如图:,平分,平分,,则下列结论:
①;②;③;④,其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
二、填空题
13.如图是我们常用的折叠式小刀,刀柄外形左侧是一个长方形的一角,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成与若,则 .
14.如图,木棒、与分别在、处用可旋转的螺丝铆住,,,将木棒绕点逆时针旋转到与木棒平行的位置,则至少要旋转
15.如图,将一块直角三角板与一张两边平行的纸条按照如图所示的方式放置,下列结论:;;;其中正确的是 填序号
16.如图是一款长臂折叠护眼灯示意图,与桌面垂直,当发光的灯管恰好与桌面平行时,,,则的度数为 °.
三、作图题
17.如图1,数学课上,老师在黑板上画出两条直线a,b,两条直线所成的角跑到黑板外面去了.老师让小明在黑板上测量出直线a,b所成的角的度数,他该怎么办?请在图2中画出测量示意图,简要说明画图方法和理由.
四、解答题
18.如图,直线 , 于 点,若 ,求 的度数.
19.如图,,交于点F,,垂足为E.
(1)若,求的度数;
(2)直接写出图中与互余的所有角.
20.如图,已知,.
(1)试问与相等吗?请说明理由;
(2)若,,求的度数.
答案解析部分
1.【答案】C
【解析】解:如图,
∵∠3=60°-∠1=60°-15°=45°,a∥b,
∴∠4=∠3=45°,
∴∠2=180°-∠3-∠4=180°-90°-45°=45°.
故答案为:C.
2.【答案】D
3.【答案】C
【解析】解:A、理由应该是两直线平行,同位角相等,故此选项错误;
B、理由应该是:内错角相等,两直线平行,故此选项错误;
C、此选项推理过程及说理都是正确的,符合题意;
D、理由应该是:同位角相等,两直线平行,故此选项错误.
故答案为:C.
4.【答案】B
【解析】解:∵ , ,
∴
∴
故答案为:B.
5.【答案】A
【解析】解:如图:
根据折叠的性质可得:∠3=∠4,
∵a//b,
∴∠1=∠3+∠4=2∠3=130°,
∴∠3=65°,
∵∠2+∠3=180°,
∴∠2=180°-∠3=180°-65°=115°,
故答案为:A .
6.【答案】A
【解析】解:∵EO⊥OF,
∴∠EOF=90°,
又∵∠BOF=55°,
∴∠EOB=90°-55°=35°,
∵AB//CD,
∴∠EOB+∠DEO=180°,
∴∠DEO=145°,
故答案为:A.
7.【答案】C
8.【答案】D
【解析】解:∵AB//CD,OG//CD,
∴OG⊥AB,
∴结论①正确;
∵AB//CD,
∴∠BOD=∠CDO=50°,
∴∠AOD=180°-∠BOD=130°,
∵OE平分∠AOD,
∴,
∴结论③正确;
∵OG⊥CD,
∴∠GOA=∠DGO=90°,
∴∠GOD=40°,∠GOE=90°-∠AOE=25°,
∴∠EOG+∠GOD=25°+40°=65°,
∵OE⊥OF,∠FOE=90°,
∴∠DOF=25°,
∴∠BOF=∠DOF,
∴OF平分∠BOD,∠GOE=∠DOF,
∴结论②④正确;
综上所述:正确的有4个,
故答案为:D.
9.【答案】A
【解析】解:∵AB∥EF,EF∥CD, ,
∴∠BEF=180°-∠1=60°,∠FEC=∠2=30°,
∴∠BEC=∠BEF+∠FEC=60°+30°=90°;
故答案为:A.
10.【答案】D
【解析】解:①由题意可得:∠G=∠MPN=90°,
∴∠G=∠MPG=90°,
∴GE//MP,
∴结论①正确;
②由题意可得:∠EFG=30°,
∴EFN=180°-∠EFG=150°,
∴结论②正确;
③过点F作FH//AB,如下图所示:
∵AB//CD, FH//AB,
∴∠BEF +∠EFH=180°,FH//CD,
∴∠HFN=MNP=45°,
∴∠EFH=∠EFN-∠HFN=105°,
∴∠BEF=180°-∠EFH=75°,
∴结论③正确;
∵∠GEF=60°,∠BEF=75°,
∴∠AEG=180°-∠GEF-∠BEF=45°,
∵∠MNP=45°,
∴∠AEG=∠PNM,
∴结论④正确,
综上所述:正确的个数是4个,
故答案为:D.
11.【答案】C
【解析】解:如图,过点C作CG∥AB,过点D作DH∥EF,如图,
∴∠BCG=α,∠EDH=γ,
∵BC⊥CD,∠CDE=β,
∴∠CDH=β-γ,∠GCD=90°-α,
∵AB∥EF,
∴AB∥CG∥DH∥EF,
∴∠GCD=∠CDH,
∴β-γ=90°-α,
∴α+β-γ=90°.
故答案为:C.
12.【答案】D
【解析】 ①由已知角平分线的条件可得∠FCA=∠ACG,∠ACB=∠ACD, ∴∠FCB= (∠ACG+∠ACD)= 180°=90°∴①正确;② 由AE=AC知∠AEC=∠ACE(等边对等角),又∠BAE= 180°-∠AEC(两直线平行同旁内角互补)同理 ∠FAC= 180°-∠ACE ∴∠BAE= ∠FAC(等角的补角相等) ②正确;③由题意知∠AEC=∠ACE=2∠ACF=2∠FCE ∴∠AQC=∠AEC+∠FCE(三角形的一个外角等于不相邻的两个内角和) ∴∠FQE=∠AQC=∠AEC+∠FCE=2∠ACF+∠ACF=3∠ACF (等量代换) ③正确;④由题意知∠AEC=∠ACE 且∠ACE=2∠FCE又∠F=∠FCE ∴∠AEC=2∠FCE=2∠F 故④正确
13.【答案】
【解析】解:过AB做A,B延长线交CD于E,如下图2
∵∠2=,刀柄左侧是一个长方形的一角
∴∠BED==
又∵AF//CD
∴∠1=∠BED=
故答案为:.
14.【答案】20
【解析】解:当∠EGB=∠EHD时,AB//CD.
∵∠EGB=100°,∠EHD=80°
∴将木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转100°-80°=20°.
故答案为:20.
15.【答案】
【解析】解:;正确,两直线平行,同位角相等
;正确,两直线平行,内错角相等
;不正确,在前两个结论正确的基础上,
正确,两直线平行,同旁内角互补。
故答案为:
16.【答案】100
【解析】解:过点E作GE∥MN,过点D作HD∥CA,如图所示:
∴∠FEG+∠NFE=180°,∠HDC+∠DCA=180°,
∵,,
∴∠HDC=70°,∠NFE=∠FEG=90°,∠GED=30°,
∵BA∥MN,
∴EG∥HD,
∴∠EDH=30°,
∴,
故答案为:100
17.【答案】解:如图,过点O作直线c∥a,测量出∠1的度数即可解决问题.
理由:由作图可知:a∥c,
∴∠1就等于直线a、b相交形成的角(两直线平行,同位角相等).
18.【答案】解:∵AB∥CD,
∴∠NMB=∠MNC=60°,
又∵MN⊥CE,
∴∠EMN=90°,
∴∠EMB=90°-∠NMB=90°-60°=30°.
19.【答案】(1)解:∵,
∴,
∵,
∴,
∴,
∴;
(2)
【解析】解:(2)解:∵,,
∴,,
即都与互余.
20.【答案】(1)解:与相等,理由如下:
∵,
,
,
同角的补角相等,
∴(内错角相等,两直线平行,
两直线平行,同位角相等
(2)解:∵,
,
,,
,即,
,,
,
即.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
