12.1 全等三角形 同步练习 (含答案)人教版数学八年级上册
文档属性
| 名称 | 12.1 全等三角形 同步练习 (含答案)人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 113.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-20 16:14:24 | ||
图片预览


文档简介
12.1 全等三角形
一、单选题
1.若△ABC≌△DEF,且△ABC的周长为20,AB=5,BC=8,则DF长为( )
A.5 B.8 C.7 D.5或8
2.已知图中的两个三角形全等,图中的字母表示三角形的边长,则∠1等于( )
A.72° B.60° C.50° D.58°
3.如图,△ABC≌△ADE,已知在△ABC中,AB边最长,BC边最短,则△ADE中三边的大小关系是( )
A.AD=AE=DE B.AD<AE<DE C.DE<AE<AD D.无法确定
4.如图,,其中,则的度数为( )
A. B. C. D.
5.如图,△ABN≌△ACM,AB=AC,BN=CM,∠B=50°,∠ANB=60°,则∠MAC的度数等于( )
A.120° B.70° C.60° D.50°.
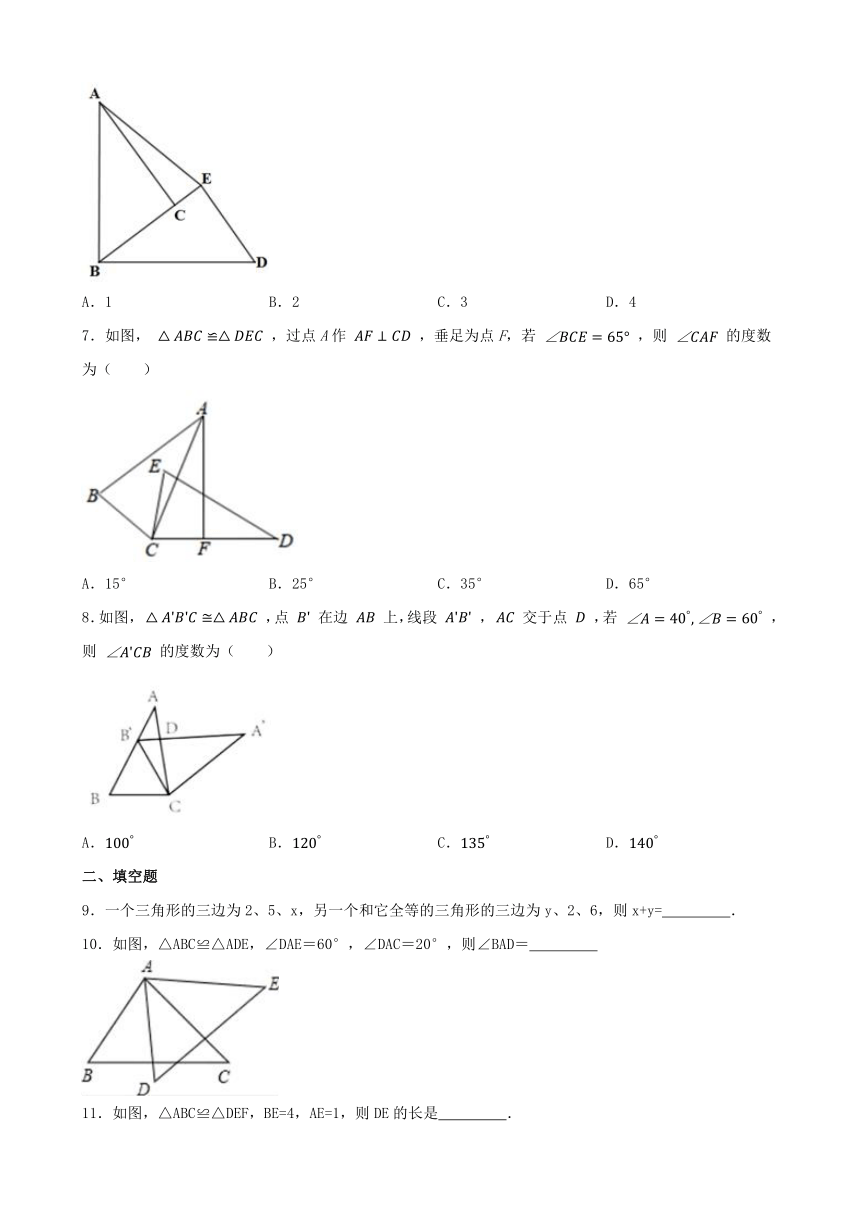
6.如图, , , , , ,CE的长为( )
A.1 B.2 C.3 D.4
7.如图, ,过点A作 ,垂足为点F,若 ,则 的度数为( )
A.15° B.25° C.35° D.65°
8.如图, ,点 在边 上,线段 , 交于点 ,若 ,则 的度数为( )
A. B. C. D.
二、填空题
9.一个三角形的三边为2、5、x,另一个和它全等的三角形的三边为y、2、6,则x+y= .
10.如图,△ABC≌△ADE,∠DAE=60°,∠DAC=20°,则∠BAD=
11.如图,△ABC≌△DEF,BE=4,AE=1,则DE的长是 .
12.如图,已知△ABC≌△ADE,∠B=25°,∠E=98°,则∠EAD的度数为 .
13.如图, ,CE=6,FC=2,则BE= .
三、解答题
14.如图,若△OAD≌△OBC,且∠0=65°,∠BEA=135°,求∠C的度数.
15.如图所示,△ABE≌△ACD,∠B=70°,∠AEB=75°,求∠CAE的度数.
16.如图12.1-4,A.B.C.D在同一直线上,且△ABF≌△DCE,那么AF∥DE、BF∥CE、AC=BD吗?为什么?
17.如图,已知 于点D, 于点E, , ,AB=8,AD=4,G为 延长线上一点,求 的度数和CE的长.
18.如图,≌,AC和AE,AB和AD是对应边,点E在边BC上,AB与DE交于点F.
(1)求证:;
(2)若,求的度数.
参考答案
1.C
2.D
3.C
4.B
5.B
6.A
7.B
8.D
9.11
10.40°
11.5
12.57°
13.14
14.解:∵△OAD≌△OBC,
∴∠C=∠D,∠OBC=∠OAD,
∵∠0=65°,
∴∠OBC=180°﹣65°﹣∠C=115°﹣∠C,
在四边形AOBE中,∠O+∠OBC+∠BEA+∠OAD=360°,
∴65°+115°﹣∠C+135°+115°﹣∠C=360°,
解得∠C=35°.
15.解:∵△ABE≌△ACD,
∴∠C=∠B=70°,
∴∠CAE=∠AEB﹣∠C=5°.
16.解答:∵△ABF≌△DCE,∴∠A=∠D,∠ABF=∠DCE,AB=CD,∴ AF//DE,∠FBC=∠ECB(等角的补角相等),AB+BC=CD+BC,∴BF//CE,AC=BD
17.解:∵△ABE≌△ACD,∠C=30°,AB=8,AD=4,
∴∠ABE=∠C=30°,
∴∠EBG=180°-∠ABE=180°-30°=150°,
∴AE=AD=4,AC=AB=8,
∴CE=AC-AE=8-4=4.
18.(1)证明:∵≌,
∴∠BAC=∠DAE,
即∠CAE+∠BAE=∠BAD+∠BAE,
∴;
(2)解:∵,,
∴∠CAE=35°,
∵≌,
∴∠C=∠AED,
∵∠AEB=∠C+∠CAE,∠AEB=∠AED+∠BED,
∴∠BED=∠CAE=35°
一、单选题
1.若△ABC≌△DEF,且△ABC的周长为20,AB=5,BC=8,则DF长为( )
A.5 B.8 C.7 D.5或8
2.已知图中的两个三角形全等,图中的字母表示三角形的边长,则∠1等于( )
A.72° B.60° C.50° D.58°
3.如图,△ABC≌△ADE,已知在△ABC中,AB边最长,BC边最短,则△ADE中三边的大小关系是( )
A.AD=AE=DE B.AD<AE<DE C.DE<AE<AD D.无法确定
4.如图,,其中,则的度数为( )
A. B. C. D.
5.如图,△ABN≌△ACM,AB=AC,BN=CM,∠B=50°,∠ANB=60°,则∠MAC的度数等于( )
A.120° B.70° C.60° D.50°.
6.如图, , , , , ,CE的长为( )
A.1 B.2 C.3 D.4
7.如图, ,过点A作 ,垂足为点F,若 ,则 的度数为( )
A.15° B.25° C.35° D.65°
8.如图, ,点 在边 上,线段 , 交于点 ,若 ,则 的度数为( )
A. B. C. D.
二、填空题
9.一个三角形的三边为2、5、x,另一个和它全等的三角形的三边为y、2、6,则x+y= .
10.如图,△ABC≌△ADE,∠DAE=60°,∠DAC=20°,则∠BAD=
11.如图,△ABC≌△DEF,BE=4,AE=1,则DE的长是 .
12.如图,已知△ABC≌△ADE,∠B=25°,∠E=98°,则∠EAD的度数为 .
13.如图, ,CE=6,FC=2,则BE= .
三、解答题
14.如图,若△OAD≌△OBC,且∠0=65°,∠BEA=135°,求∠C的度数.
15.如图所示,△ABE≌△ACD,∠B=70°,∠AEB=75°,求∠CAE的度数.
16.如图12.1-4,A.B.C.D在同一直线上,且△ABF≌△DCE,那么AF∥DE、BF∥CE、AC=BD吗?为什么?
17.如图,已知 于点D, 于点E, , ,AB=8,AD=4,G为 延长线上一点,求 的度数和CE的长.
18.如图,≌,AC和AE,AB和AD是对应边,点E在边BC上,AB与DE交于点F.
(1)求证:;
(2)若,求的度数.
参考答案
1.C
2.D
3.C
4.B
5.B
6.A
7.B
8.D
9.11
10.40°
11.5
12.57°
13.14
14.解:∵△OAD≌△OBC,
∴∠C=∠D,∠OBC=∠OAD,
∵∠0=65°,
∴∠OBC=180°﹣65°﹣∠C=115°﹣∠C,
在四边形AOBE中,∠O+∠OBC+∠BEA+∠OAD=360°,
∴65°+115°﹣∠C+135°+115°﹣∠C=360°,
解得∠C=35°.
15.解:∵△ABE≌△ACD,
∴∠C=∠B=70°,
∴∠CAE=∠AEB﹣∠C=5°.
16.解答:∵△ABF≌△DCE,∴∠A=∠D,∠ABF=∠DCE,AB=CD,∴ AF//DE,∠FBC=∠ECB(等角的补角相等),AB+BC=CD+BC,∴BF//CE,AC=BD
17.解:∵△ABE≌△ACD,∠C=30°,AB=8,AD=4,
∴∠ABE=∠C=30°,
∴∠EBG=180°-∠ABE=180°-30°=150°,
∴AE=AD=4,AC=AB=8,
∴CE=AC-AE=8-4=4.
18.(1)证明:∵≌,
∴∠BAC=∠DAE,
即∠CAE+∠BAE=∠BAD+∠BAE,
∴;
(2)解:∵,,
∴∠CAE=35°,
∵≌,
∴∠C=∠AED,
∵∠AEB=∠C+∠CAE,∠AEB=∠AED+∠BED,
∴∠BED=∠CAE=35°
