2025苏教版高中数学必修第一册同步练习题--5.2 函数的表示方法(含解析)
文档属性
| 名称 | 2025苏教版高中数学必修第一册同步练习题--5.2 函数的表示方法(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 471.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-23 17:41:19 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025苏教版高中数学必修第一册
5.2 函数的表示方法
基础过关练
题组一 函数的表示方法
1.(2024江苏南京第九中学阶段检测)若函数f(x)和g(x)分别由下表给出,满足g(f(x))=2的x值是( )
x 1 2 3 4
f(x) 2 3 4 1
g(x) 2 1 4 3
A.1 B.2 C.3 D.4
2.(2024广西南宁联考)函数y=g(x)的对应关系如表所示,函数y=f(x)的图象是如图所示的曲线ABC,则g(f(3)-1)的值为( )
x 1 2 3
g(x) 2 023 0 -2 023
A.2 023 B.0
C.-1 D.-2 023
3.(2023天津滨海新区期中)下图中的文物叫作“垂鳞纹圆壶”,是甘肃礼县出土的先秦时期的青铜器皿,其身流线自若、纹理分明,展现了古代中国精湛的制造技术.科研人员为了测量其容积,以恒定的流速向其内注水,恰好用时30秒注满.设注水过程中,壶中水面高度为h,注水时间为t,则下面选项中最符合h关于t的函数图象的是( )
A B
C D
4.(2023江苏无锡期末)某条公共汽车路线收支差额y关于乘客量x的图象如图(1)所示,由于目前本条路线亏损,公司有关人员提出了两种扭亏为盈的建议,如图(2)、图(3),则下列说法错误的是( )
A.图(1)中的点A表示当乘客量为0时,亏损1.5个单位
B.图(1)中的点B表示当乘客量为3时,既不亏损也不盈利
C.图(2)的建议为降低成本,提高票价
D.图(3)的建议为保持成本,提高票价
题组二 函数解析式的求法
5.(2024江苏阜宁中学期中)已知函数f(-2)=x-4+5,则f(x)的解析式为( )
A.f(x)=x2+1(x≥0) B.f(x)=x2+1(x≥-2)
C.f(x)=x2(x≥0) D.f(x)=x2(x≥-2)
6.(2024辽宁沈阳第十五中阶段检测)若g(x)=1-2x, f(g(x))=(x≠0),则f 等于( )
A.1 B.2 C.15 D.30
7.(2024江西南昌期中)已知f(x)是一次函数,若f(f(x))=4x+9,则f(x)的解析式为 .
8.(2022江苏宿豫中学月考)已知f(x)是二次函数,且f(x+1)+f(x-1)=2x2-4x,则f(x)= .
题组三 分段函数
9.(教材习题改编)已知函数f(x)=则f(1)=( )
A.1 B.0 C.-1 D.-2
10.(2024江苏镇江期中)已知函数f(x)=若f(f(0))=-2,则实数a=( )
A.2 B.3 C.4 D.5
11.(2023江苏宿迁第一高级中学期中)已知函数f(x)=则f(x)的值域为( )
A.[0,2] B.(0,+∞)
C. D.
12.(2024江苏句容高级中学阶段检测)已知f(x)=若f(a)<-3,则a的取值范围为( )
A.(-3,+∞) B.[-3,+∞)
C.(-∞,-3) D.(-∞,-3]
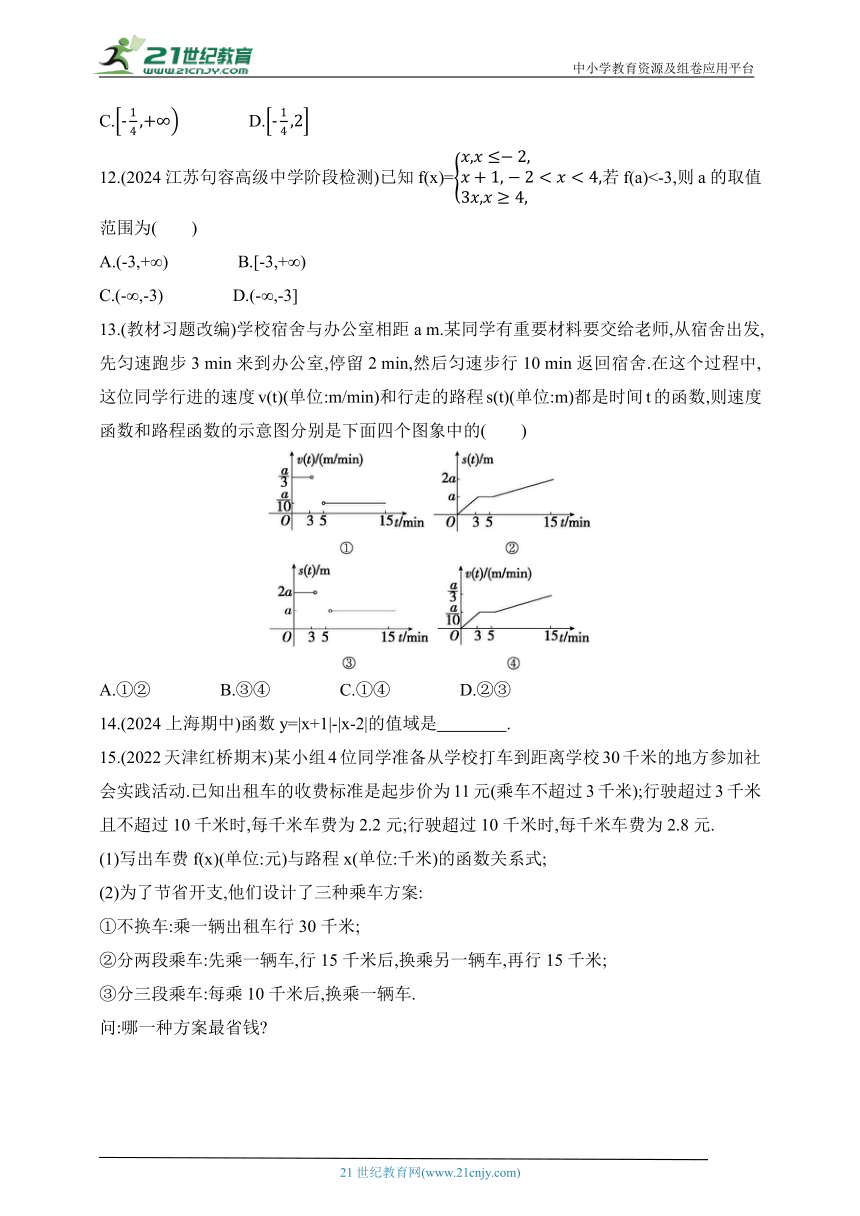
13.(教材习题改编)学校宿舍与办公室相距a m.某同学有重要材料要交给老师,从宿舍出发,先匀速跑步3 min来到办公室,停留2 min,然后匀速步行10 min返回宿舍.在这个过程中,这位同学行进的速度v(t)(单位:m/min)和行走的路程s(t)(单位:m)都是时间t的函数,则速度函数和路程函数的示意图分别是下面四个图象中的( )
A.①② B.③④ C.①④ D.②③
14.(2024上海期中)函数y=|x+1|-|x-2|的值域是 .
15.(2022天津红桥期末)某小组4位同学准备从学校打车到距离学校30千米的地方参加社会实践活动.已知出租车的收费标准是起步价为11元(乘车不超过3千米);行驶超过3千米且不超过10千米时,每千米车费为2.2元;行驶超过10千米时,每千米车费为2.8元.
(1)写出车费f(x)(单位:元)与路程x(单位:千米)的函数关系式;
(2)为了节省开支,他们设计了三种乘车方案:
①不换车:乘一辆出租车行30千米;
②分两段乘车:先乘一辆车,行15千米后,换乘另一辆车,再行15千米;
③分三段乘车:每乘10千米后,换乘一辆车.
问:哪一种方案最省钱
能力提升练
题组一 函数的表示方法及其应用
1.某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表,则各班推选代表人数y与该班人数x之间的函数关系用取整函数y=[x]([x]表示不大于x的最大整数,如[π]=3,[4]=4)可表示为( )
A.y= B.y=
C.y= D.y=
2.(2023河南省实验中学月考)如图,在△ABC中,∠ACB=90°,∠A=30°,AB=16,点P是斜边AB上的任意一点(不与点A,B重合),过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x(0A B
C D
3.(2024江苏常州北郊高级中学期末)已知函数f(x),g(x)分别由下表给出:
x 1 2 3
f(x) 1 3 1
g(x) 3 2 1
满足f(g(x))题组二 函数解析式的求法
4.(2024江苏海安高级中学阶段检测)已知函数f(x)的定义域为(0,+∞),且满足f(x)+2f =5x+,则f(x)的最小值为( )
A.2 B.3 C.4 D.2
5.下图中所表示的函数的解析式为( )
A.y=|x-1|(0≤x≤2)
B.y=-|x-1|(0≤x≤2)
C.y=-|x-1|(0≤x≤2)
D.y=1-|x-1|(0≤x≤2)
6.(多选题)(2024江苏常州期中)已知函数f(x)=x3+ax2+bx+c,且-3A.a=-2 B.b=1
C.07.(多选题)(2024浙江期中)已知函数f(x)的定义域为R,且f(x)=x3f ,x∈(-∞,0)∪(0,+∞),若f(x)+f(y)+xy=f(x+y),则下列说法正确的是( )
A.f(0)=0 B.f(3)=3
C.f(x)-f(-x)=x D.f(x)=
8.(2022江苏如东高级中学阶段测试)f(x)是R上的函数,且满足f(0)=1,并且对任意的实数x,y都有f(x-y)=f(x)-y(2x-y+1),则f(x)的解析式为 .
题组三 分段函数及其应用
9.(多选题)(2024湖南长沙明德中学阶段检测)如图所示,函数f(x)的图象由两条线段组成,则下列关于函数f(x)的说法正确的是( )
A.f(2)>f(0)
B.f(f(1))=3
C.f(x)=2|x-1|-x+1,x∈[0,4]
D. a>0,不等式f(x)≤a的解集为
10.(2024江苏南通期中)已知函数f(x)=满足f(f(a))=1的a的值有( )
A.1个 B.2个
C.3个 D.4个
11.(2024江苏淮安期中)已知f(x)=x2-1,g(x)=则函数y=f(x)·g(x)的值域为( )
A.[-1,+∞) B.[0,+∞)
C.(-∞,-1] D.(-∞,0]
12.(2024江苏常州高级中学期中)已知函数f(x)=若f(x)的值域为[-2,2],则实数c的值是 .
13.已知λ∈R,函数f(x)=当λ=2时,不等式f(x)<0的解集是 .若函数f(x)的图象与x轴恰有2个交点,则λ的取值范围是 .
14.(2023江苏南京第一中学检测)快递行业的发展使得网络购物越来越便利,根据大数据统计,某条快递线路运行时,发车时间间隔t(单位:分钟)满足4≤t≤15,t∈N,平均每趟快递车辆的载件量p(t)(单位:个)与发车时间间隔t(单位:分钟)近似地满足p(t)=其中t∈N.
(1)若平均每趟快递车辆的载件量不超过1 500个,求发车时间间隔;
(2)若平均每趟快递车辆每分钟的净收益q(t)=-80(单位:元),问当发车时间间隔为多少时,平均每趟快递车辆每分钟的净收益最大 并求出最大净收益.
答案与分层梯度式解析
5.2 函数的表示方法
基础过关练
1.D 由g(f(x))=2,得f(x)=1,则x=4.故选D.
2.A 由题图可知, f(3)=2,则g(f(3)-1)=g(2-1)=g(1)=2 023.故选A.
3.A 由题图知,“垂鳞纹圆壶”中间粗,两端细,所以在注水速度恒定的情况下,水的高度开始增加得快,后来增加得慢,最后又增加得快.故选A.
4.C 由题图(1)知,显然A,B正确;对于C,由题图(2)知,两直线平行,所以票价不变,直线向上平移,说明当乘客量为0时,收支差额变大了,即支出变少了,所以题图(2)的建议为降低成本,票价不变,故C错误;对于D,由题图(3)知,当乘客量为0时,支出不变,所以成本不变,直线的倾斜角变大了,即每增加一位乘客,收支差额的增加值变大了,所以票价提高了,所以题图(3)的建议为保持成本,提高票价,故D正确.故选C.
5.B 解法一(配凑法):f(-2)=(-2)2+1,所以f(x)=x2+1(x≥-2).故选B.
解法二(换元法):令t=-2,则t≥-2,x=(t+2)2,
所以f(t)=(t+2)2-4(t+2)+5=t2+1,
所以f(x)=x2+1(x≥-2).故选B.
6.C 解法一:易知f(1-2x)=(x≠0),
令t=1-2x(x≠0),则t≠1,x=,
所以f(t)==(t≠1),
所以f ==15.故选C.
解法二:易知f(1-2x)=(x≠0),令1-2x=,
则x=,所以f ==15.故选C.
7.答案 f(x)=2x+3或f(x)=-2x-9
解析 依题意,设f(x)=kx+b(k≠0),则f(f(x))=kf(x)+b=k(kx+b)+b=k2x+(k+1)b(k≠0),
又因为f(f(x))=4x+9,所以
解得或
所以f(x)的解析式为f(x)=2x+3或f(x)=-2x-9.
8.答案 x2-2x-1
解析 设f(x)=ax2+bx+c(a≠0),则f(x+1)=a(x+1)2+b(x+1)+c=ax2+(2a+b)x+a+b+c, f(x-1)=a(x-1)2+b(x-1)+c=ax2+(-2a+b)x+a-b+c,所以f(x+1)+f(x-1)=2ax2+2bx+2a+2c,
又f(x+1)+f(x-1)=2x2-4x,所以解得所以f(x)=x2-2x-1.
9.B ∵f(x)=∴f(1)=f(-1)=(-1)2-1=0.故选B.
10.B 由题知f(0)=1, f(1)=1-a,∵f(f(0))=-2,∴f(1)=1-a=-2,∴a=3.
故选B.
11.C 当x<0时,-∈(0,+∞);当0≤x≤2时,x2-x=-∈,所以函数f(x)的值域为.故选C.
12.C (分a≤-2,-2已知f(x)=
①当a≤-2时, f(a)=a,
由f(a)<-3,得a<-3;
②当-2由f(a)<-3,得a+1<-3,解得a<-4,此时不等式无解;
③当a≥4时, f(a)=3a,
由f(a)<-3,得3a<-3,解得a<-1,此时不等式无解.
综上,a的取值范围是(-∞,-3).故选C.
13.A 根据题意,得v(t)=且s(t)=
由速度函数及路程函数的解析式可知,其图象分别为①②.故选A.
14.答案 [-3,3]
解析 由y=|x+1|-|x-2|=
当-1≤x≤2时,y=2x-1单调递增,所以-3≤y≤3,
故函数y=|x+1|-|x-2|的值域为[-3,3].
15.解析 (1)由题意得,当0当3当x>10时, f(x)=11+(10-3)×2.2+(x-10)×2.8=2.8x-1.6.
所以f(x)=
(2)方案①: f(30)=2.8×30-1.6=82.4(元);
方案②:2f(15)=2×(2.8×15-1.6)=80.8(元);
方案③:3f(10)=3×(2.2×10+4.4)=79.2(元).
因为82.4>80.8>79.2,所以方案③最省钱.
能力提升练
1.B 因为各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表,所以当余数为7,8,9时可增选一名代表,即x要进一位,故最小应加3,因此利用取整函数可表示为y=.故选B.
2.D 过点C作CD⊥AB交AB于点D,因为∠ACB=90°,∠A=30°,AB=16,所以∠B=60°,BC=8,所以BD=BC=4,AD=AB-BD=12.
如图1,当0如图2,当12图1 图2
3.答案 {1,3}
解析 当x=1时, f(g(1))=f(3)=1,g(f(1))=g(1)=3,故f(g(1))当x=2时, f(g(2))=f(2)=3,g(f(2))=g(3)=1,故f(g(2))>g(f(2)),不满足要求;
当x=3时, f(g(3))=f(1)=1,g(f(3))=g(1)=3,故f(g(3))故满足f(g(x))4.D 因为f(x)+2f =5x+①,
所以f +2f(x)=+4x②,
②×2-①,得f(x)=x+,
又x∈(0,+∞),
所以f(x)=x+≥2=2,
当且仅当x=,即x=时取等号,
所以f(x)的最小值为2.故选D.
5.B 当0≤x≤1时,设y=kx,由题中图象过点,得k=,所以y=x,0≤x≤1;
当1所以y=-x+3,16.AD 由题意,设f(-1)=f(1)=f(2)=m,
则-1,1,2是方程f(x)-m=0的3个根,
又f(x)=x3+ax2+bx+c,
所以f(x)-m=(x+1)(x-1)(x-2),
即f(x)=(x+1)(x-1)(x-2)+m,且-3所以f(x)=x3-2x2-x+m+2,
故a=-2,b=-1,c=m+2,故A正确,B错误;
由-3故C错误,D正确.故选AD.
7.AC 在f(x)+f(y)+xy=f(x+y)中,令x=y=0,
则f(0)=0,故A正确;
令y=-x,则f(x)+f(-x)-x2=f(0)=0,即f(x)+f(-x)=x2①,
所以f +f =,即f =-f ,又f(x)=x3f ,所以f(x)=x3=x-x3f =x+f(-x),即f(x)-f(-x)=x(x≠0)②,
又f(0)=0也符合上式,故C正确;
联立①②,解得f(x)=,故D错误;
f(3)=6,故B错误.
故选AC.
8.答案 f(x)=x2+x+1
解析 令x=0,则f(-y)=f(0)-y(-y+1),
∵f(0)=1,∴f(-y)=1-y(-y+1)=y2-y+1=(-y)2+(-y)+1,∴f(x)=x2+x+1.
9.BC 由题图可知,函数f(x)为分段函数,其图象过点(0,3),(1,0),(4,3),
当0≤x<1时,设f(x)=kx+b(k≠0),
将(0,3),(1,0)代入f(x)=kx+b,得
解得所以f(x)=-3x+3;
当1≤x≤4时,设f(x)=mx+n(m≠0),
将(1,0),(4,3)代入f(x)=mx+n,得
解得所以f(x)=x-1.
故f(x)=
对于A, f(2)=1对于B, f(f(1))=f(0)=3,故B正确;
对于C,因为f(x)=2|x-1|-x+1,x∈[0,4],
所以当0≤x<1时, f(x)=2(1-x)-x+1=-3x+3,
当1≤x≤4时, f(x)=2(x-1)-x+1=x-1,故C正确;
对于D,由题意知,f =f(2)=a,因为f =2, f(2)=1,所以f ≠f(2),所以不存在a>0,使得不等式f(x)≤a的解集为,故D错误.
故选BC.
10.B 根据题意,函数f(x)=
当x≤0时, f(x)=x2+2x+1=(x+1)2≥0,
当x>0时, f(x)=-x2<0,
若f(f(a))=1,必有f(a)≤0,
则f(f(a))=[f(a)+1]2=1,解得f(a)=0或f(a)=-2,
若f(a)=0,必有a≤0,
则f(a)=(a+1)2=0,解得a=-1,
若f(a)=-2,必有a>0,
则f(a)=-a2=-2,解得a=(负值舍去),
故a=-1或a=.故选B.
11.D 当f(x)>0时,x2-1>0,解得x∈(-∞,-1)∪(1,+∞),此时g(x)=-1,
所以y=-(x2-1)=1-x2,因为x∈(-∞,-1)∪(1,+∞),所以y∈(-∞,0);
当f(x)=0时,x2-1=0,解得x=±1,此时g(x)=0,所以y=0;
当f(x)<0时,x2-1<0,解得x∈(-1,1),此时g(x)=1,
所以y=x2-1,因为x∈(-1,1),所以y∈[-1,0).
综上可知,y∈(-∞,0].故选D.
12.答案 -
解析 若c>0,则当0若c=0,则当x<0时, f(x)=-∈(0,+∞),不满足题意;
若c<0,则当x≤c时,0<-≤-,即f(x)∈,
当c当x=2时, f(2)=2-4=-2,
令f(c)=-2,则c-c2=-2,解得c=-1或c=2(舍去),
令f(c)=0,则c-c2=0,解得c=0或c=1,
作出y=f(x)的大致图象,如图,
因为f(x)的值域为[-2,2],所以-=2,解得c=-,经检验,满足题意.
13.答案 (1,4);(1,3]∪(4,+∞)
解析 当λ=2时,不等式f(x)<0等价于或解得2≤x<4或1故不等式f(x)<0的解集为(1,4).
易知函数y=x-4(x∈R)的图象与x轴交点的横坐标为4,函数y=x2-4x+3(x∈R)的图象与x轴交点的横坐标分别为1,3.
在同一平面直角坐标系中作出函数y=x-4和y=x2-4x+3的图象(图略),要使函数f(x)的图象与x轴恰有2个交点,则只能有以下两种情形:①两个交点的横坐标分别为1,3,此时λ>4;②两个交点的横坐标分别为1,4,此时1<λ≤3.
综上,λ的取值范围为(1,3]∪(4,+∞).
14.解析 (1)当9≤t≤15时,p(t)=1 800>1 500,不满足题意,舍去.
当4≤t<9时,令1 800-15(9-t)2≤1 500,即t2-18t+61≥0,解得t≥9+2(舍去)或t≤9-2.
因为4≤t<9且t∈N,所以t=4.
所以发车时间间隔为4分钟.
(2)由题意得q(t)=
当4≤t<9时,q(t)≤-2+1 540=280,当且仅当90t=,即t=7时,等号成立.
当9≤t≤15时,q(t)≤-80=240.
因为280>240,所以当发车时间间隔为7分钟时,平均每趟快递车辆每分钟的净收益最大,最大净收益为280元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025苏教版高中数学必修第一册
5.2 函数的表示方法
基础过关练
题组一 函数的表示方法
1.(2024江苏南京第九中学阶段检测)若函数f(x)和g(x)分别由下表给出,满足g(f(x))=2的x值是( )
x 1 2 3 4
f(x) 2 3 4 1
g(x) 2 1 4 3
A.1 B.2 C.3 D.4
2.(2024广西南宁联考)函数y=g(x)的对应关系如表所示,函数y=f(x)的图象是如图所示的曲线ABC,则g(f(3)-1)的值为( )
x 1 2 3
g(x) 2 023 0 -2 023
A.2 023 B.0
C.-1 D.-2 023
3.(2023天津滨海新区期中)下图中的文物叫作“垂鳞纹圆壶”,是甘肃礼县出土的先秦时期的青铜器皿,其身流线自若、纹理分明,展现了古代中国精湛的制造技术.科研人员为了测量其容积,以恒定的流速向其内注水,恰好用时30秒注满.设注水过程中,壶中水面高度为h,注水时间为t,则下面选项中最符合h关于t的函数图象的是( )
A B
C D
4.(2023江苏无锡期末)某条公共汽车路线收支差额y关于乘客量x的图象如图(1)所示,由于目前本条路线亏损,公司有关人员提出了两种扭亏为盈的建议,如图(2)、图(3),则下列说法错误的是( )
A.图(1)中的点A表示当乘客量为0时,亏损1.5个单位
B.图(1)中的点B表示当乘客量为3时,既不亏损也不盈利
C.图(2)的建议为降低成本,提高票价
D.图(3)的建议为保持成本,提高票价
题组二 函数解析式的求法
5.(2024江苏阜宁中学期中)已知函数f(-2)=x-4+5,则f(x)的解析式为( )
A.f(x)=x2+1(x≥0) B.f(x)=x2+1(x≥-2)
C.f(x)=x2(x≥0) D.f(x)=x2(x≥-2)
6.(2024辽宁沈阳第十五中阶段检测)若g(x)=1-2x, f(g(x))=(x≠0),则f 等于( )
A.1 B.2 C.15 D.30
7.(2024江西南昌期中)已知f(x)是一次函数,若f(f(x))=4x+9,则f(x)的解析式为 .
8.(2022江苏宿豫中学月考)已知f(x)是二次函数,且f(x+1)+f(x-1)=2x2-4x,则f(x)= .
题组三 分段函数
9.(教材习题改编)已知函数f(x)=则f(1)=( )
A.1 B.0 C.-1 D.-2
10.(2024江苏镇江期中)已知函数f(x)=若f(f(0))=-2,则实数a=( )
A.2 B.3 C.4 D.5
11.(2023江苏宿迁第一高级中学期中)已知函数f(x)=则f(x)的值域为( )
A.[0,2] B.(0,+∞)
C. D.
12.(2024江苏句容高级中学阶段检测)已知f(x)=若f(a)<-3,则a的取值范围为( )
A.(-3,+∞) B.[-3,+∞)
C.(-∞,-3) D.(-∞,-3]
13.(教材习题改编)学校宿舍与办公室相距a m.某同学有重要材料要交给老师,从宿舍出发,先匀速跑步3 min来到办公室,停留2 min,然后匀速步行10 min返回宿舍.在这个过程中,这位同学行进的速度v(t)(单位:m/min)和行走的路程s(t)(单位:m)都是时间t的函数,则速度函数和路程函数的示意图分别是下面四个图象中的( )
A.①② B.③④ C.①④ D.②③
14.(2024上海期中)函数y=|x+1|-|x-2|的值域是 .
15.(2022天津红桥期末)某小组4位同学准备从学校打车到距离学校30千米的地方参加社会实践活动.已知出租车的收费标准是起步价为11元(乘车不超过3千米);行驶超过3千米且不超过10千米时,每千米车费为2.2元;行驶超过10千米时,每千米车费为2.8元.
(1)写出车费f(x)(单位:元)与路程x(单位:千米)的函数关系式;
(2)为了节省开支,他们设计了三种乘车方案:
①不换车:乘一辆出租车行30千米;
②分两段乘车:先乘一辆车,行15千米后,换乘另一辆车,再行15千米;
③分三段乘车:每乘10千米后,换乘一辆车.
问:哪一种方案最省钱
能力提升练
题组一 函数的表示方法及其应用
1.某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表,则各班推选代表人数y与该班人数x之间的函数关系用取整函数y=[x]([x]表示不大于x的最大整数,如[π]=3,[4]=4)可表示为( )
A.y= B.y=
C.y= D.y=
2.(2023河南省实验中学月考)如图,在△ABC中,∠ACB=90°,∠A=30°,AB=16,点P是斜边AB上的任意一点(不与点A,B重合),过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x(0
C D
3.(2024江苏常州北郊高级中学期末)已知函数f(x),g(x)分别由下表给出:
x 1 2 3
f(x) 1 3 1
g(x) 3 2 1
满足f(g(x))
4.(2024江苏海安高级中学阶段检测)已知函数f(x)的定义域为(0,+∞),且满足f(x)+2f =5x+,则f(x)的最小值为( )
A.2 B.3 C.4 D.2
5.下图中所表示的函数的解析式为( )
A.y=|x-1|(0≤x≤2)
B.y=-|x-1|(0≤x≤2)
C.y=-|x-1|(0≤x≤2)
D.y=1-|x-1|(0≤x≤2)
6.(多选题)(2024江苏常州期中)已知函数f(x)=x3+ax2+bx+c,且-3
C.0
A.f(0)=0 B.f(3)=3
C.f(x)-f(-x)=x D.f(x)=
8.(2022江苏如东高级中学阶段测试)f(x)是R上的函数,且满足f(0)=1,并且对任意的实数x,y都有f(x-y)=f(x)-y(2x-y+1),则f(x)的解析式为 .
题组三 分段函数及其应用
9.(多选题)(2024湖南长沙明德中学阶段检测)如图所示,函数f(x)的图象由两条线段组成,则下列关于函数f(x)的说法正确的是( )
A.f(2)>f(0)
B.f(f(1))=3
C.f(x)=2|x-1|-x+1,x∈[0,4]
D. a>0,不等式f(x)≤a的解集为
10.(2024江苏南通期中)已知函数f(x)=满足f(f(a))=1的a的值有( )
A.1个 B.2个
C.3个 D.4个
11.(2024江苏淮安期中)已知f(x)=x2-1,g(x)=则函数y=f(x)·g(x)的值域为( )
A.[-1,+∞) B.[0,+∞)
C.(-∞,-1] D.(-∞,0]
12.(2024江苏常州高级中学期中)已知函数f(x)=若f(x)的值域为[-2,2],则实数c的值是 .
13.已知λ∈R,函数f(x)=当λ=2时,不等式f(x)<0的解集是 .若函数f(x)的图象与x轴恰有2个交点,则λ的取值范围是 .
14.(2023江苏南京第一中学检测)快递行业的发展使得网络购物越来越便利,根据大数据统计,某条快递线路运行时,发车时间间隔t(单位:分钟)满足4≤t≤15,t∈N,平均每趟快递车辆的载件量p(t)(单位:个)与发车时间间隔t(单位:分钟)近似地满足p(t)=其中t∈N.
(1)若平均每趟快递车辆的载件量不超过1 500个,求发车时间间隔;
(2)若平均每趟快递车辆每分钟的净收益q(t)=-80(单位:元),问当发车时间间隔为多少时,平均每趟快递车辆每分钟的净收益最大 并求出最大净收益.
答案与分层梯度式解析
5.2 函数的表示方法
基础过关练
1.D 由g(f(x))=2,得f(x)=1,则x=4.故选D.
2.A 由题图可知, f(3)=2,则g(f(3)-1)=g(2-1)=g(1)=2 023.故选A.
3.A 由题图知,“垂鳞纹圆壶”中间粗,两端细,所以在注水速度恒定的情况下,水的高度开始增加得快,后来增加得慢,最后又增加得快.故选A.
4.C 由题图(1)知,显然A,B正确;对于C,由题图(2)知,两直线平行,所以票价不变,直线向上平移,说明当乘客量为0时,收支差额变大了,即支出变少了,所以题图(2)的建议为降低成本,票价不变,故C错误;对于D,由题图(3)知,当乘客量为0时,支出不变,所以成本不变,直线的倾斜角变大了,即每增加一位乘客,收支差额的增加值变大了,所以票价提高了,所以题图(3)的建议为保持成本,提高票价,故D正确.故选C.
5.B 解法一(配凑法):f(-2)=(-2)2+1,所以f(x)=x2+1(x≥-2).故选B.
解法二(换元法):令t=-2,则t≥-2,x=(t+2)2,
所以f(t)=(t+2)2-4(t+2)+5=t2+1,
所以f(x)=x2+1(x≥-2).故选B.
6.C 解法一:易知f(1-2x)=(x≠0),
令t=1-2x(x≠0),则t≠1,x=,
所以f(t)==(t≠1),
所以f ==15.故选C.
解法二:易知f(1-2x)=(x≠0),令1-2x=,
则x=,所以f ==15.故选C.
7.答案 f(x)=2x+3或f(x)=-2x-9
解析 依题意,设f(x)=kx+b(k≠0),则f(f(x))=kf(x)+b=k(kx+b)+b=k2x+(k+1)b(k≠0),
又因为f(f(x))=4x+9,所以
解得或
所以f(x)的解析式为f(x)=2x+3或f(x)=-2x-9.
8.答案 x2-2x-1
解析 设f(x)=ax2+bx+c(a≠0),则f(x+1)=a(x+1)2+b(x+1)+c=ax2+(2a+b)x+a+b+c, f(x-1)=a(x-1)2+b(x-1)+c=ax2+(-2a+b)x+a-b+c,所以f(x+1)+f(x-1)=2ax2+2bx+2a+2c,
又f(x+1)+f(x-1)=2x2-4x,所以解得所以f(x)=x2-2x-1.
9.B ∵f(x)=∴f(1)=f(-1)=(-1)2-1=0.故选B.
10.B 由题知f(0)=1, f(1)=1-a,∵f(f(0))=-2,∴f(1)=1-a=-2,∴a=3.
故选B.
11.C 当x<0时,-∈(0,+∞);当0≤x≤2时,x2-x=-∈,所以函数f(x)的值域为.故选C.
12.C (分a≤-2,-2
①当a≤-2时, f(a)=a,
由f(a)<-3,得a<-3;
②当-2
③当a≥4时, f(a)=3a,
由f(a)<-3,得3a<-3,解得a<-1,此时不等式无解.
综上,a的取值范围是(-∞,-3).故选C.
13.A 根据题意,得v(t)=且s(t)=
由速度函数及路程函数的解析式可知,其图象分别为①②.故选A.
14.答案 [-3,3]
解析 由y=|x+1|-|x-2|=
当-1≤x≤2时,y=2x-1单调递增,所以-3≤y≤3,
故函数y=|x+1|-|x-2|的值域为[-3,3].
15.解析 (1)由题意得,当0
所以f(x)=
(2)方案①: f(30)=2.8×30-1.6=82.4(元);
方案②:2f(15)=2×(2.8×15-1.6)=80.8(元);
方案③:3f(10)=3×(2.2×10+4.4)=79.2(元).
因为82.4>80.8>79.2,所以方案③最省钱.
能力提升练
1.B 因为各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表,所以当余数为7,8,9时可增选一名代表,即x要进一位,故最小应加3,因此利用取整函数可表示为y=.故选B.
2.D 过点C作CD⊥AB交AB于点D,因为∠ACB=90°,∠A=30°,AB=16,所以∠B=60°,BC=8,所以BD=BC=4,AD=AB-BD=12.
如图1,当0
3.答案 {1,3}
解析 当x=1时, f(g(1))=f(3)=1,g(f(1))=g(1)=3,故f(g(1))
当x=3时, f(g(3))=f(1)=1,g(f(3))=g(1)=3,故f(g(3))
所以f +2f(x)=+4x②,
②×2-①,得f(x)=x+,
又x∈(0,+∞),
所以f(x)=x+≥2=2,
当且仅当x=,即x=时取等号,
所以f(x)的最小值为2.故选D.
5.B 当0≤x≤1时,设y=kx,由题中图象过点,得k=,所以y=x,0≤x≤1;
当1
则-1,1,2是方程f(x)-m=0的3个根,
又f(x)=x3+ax2+bx+c,
所以f(x)-m=(x+1)(x-1)(x-2),
即f(x)=(x+1)(x-1)(x-2)+m,且-3
故a=-2,b=-1,c=m+2,故A正确,B错误;
由-3
7.AC 在f(x)+f(y)+xy=f(x+y)中,令x=y=0,
则f(0)=0,故A正确;
令y=-x,则f(x)+f(-x)-x2=f(0)=0,即f(x)+f(-x)=x2①,
所以f +f =,即f =-f ,又f(x)=x3f ,所以f(x)=x3=x-x3f =x+f(-x),即f(x)-f(-x)=x(x≠0)②,
又f(0)=0也符合上式,故C正确;
联立①②,解得f(x)=,故D错误;
f(3)=6,故B错误.
故选AC.
8.答案 f(x)=x2+x+1
解析 令x=0,则f(-y)=f(0)-y(-y+1),
∵f(0)=1,∴f(-y)=1-y(-y+1)=y2-y+1=(-y)2+(-y)+1,∴f(x)=x2+x+1.
9.BC 由题图可知,函数f(x)为分段函数,其图象过点(0,3),(1,0),(4,3),
当0≤x<1时,设f(x)=kx+b(k≠0),
将(0,3),(1,0)代入f(x)=kx+b,得
解得所以f(x)=-3x+3;
当1≤x≤4时,设f(x)=mx+n(m≠0),
将(1,0),(4,3)代入f(x)=mx+n,得
解得所以f(x)=x-1.
故f(x)=
对于A, f(2)=1
对于C,因为f(x)=2|x-1|-x+1,x∈[0,4],
所以当0≤x<1时, f(x)=2(1-x)-x+1=-3x+3,
当1≤x≤4时, f(x)=2(x-1)-x+1=x-1,故C正确;
对于D,由题意知,f =f(2)=a,因为f =2, f(2)=1,所以f ≠f(2),所以不存在a>0,使得不等式f(x)≤a的解集为,故D错误.
故选BC.
10.B 根据题意,函数f(x)=
当x≤0时, f(x)=x2+2x+1=(x+1)2≥0,
当x>0时, f(x)=-x2<0,
若f(f(a))=1,必有f(a)≤0,
则f(f(a))=[f(a)+1]2=1,解得f(a)=0或f(a)=-2,
若f(a)=0,必有a≤0,
则f(a)=(a+1)2=0,解得a=-1,
若f(a)=-2,必有a>0,
则f(a)=-a2=-2,解得a=(负值舍去),
故a=-1或a=.故选B.
11.D 当f(x)>0时,x2-1>0,解得x∈(-∞,-1)∪(1,+∞),此时g(x)=-1,
所以y=-(x2-1)=1-x2,因为x∈(-∞,-1)∪(1,+∞),所以y∈(-∞,0);
当f(x)=0时,x2-1=0,解得x=±1,此时g(x)=0,所以y=0;
当f(x)<0时,x2-1<0,解得x∈(-1,1),此时g(x)=1,
所以y=x2-1,因为x∈(-1,1),所以y∈[-1,0).
综上可知,y∈(-∞,0].故选D.
12.答案 -
解析 若c>0,则当0
若c<0,则当x≤c时,0<-≤-,即f(x)∈,
当c
令f(c)=-2,则c-c2=-2,解得c=-1或c=2(舍去),
令f(c)=0,则c-c2=0,解得c=0或c=1,
作出y=f(x)的大致图象,如图,
因为f(x)的值域为[-2,2],所以-=2,解得c=-,经检验,满足题意.
13.答案 (1,4);(1,3]∪(4,+∞)
解析 当λ=2时,不等式f(x)<0等价于或解得2≤x<4或1
易知函数y=x-4(x∈R)的图象与x轴交点的横坐标为4,函数y=x2-4x+3(x∈R)的图象与x轴交点的横坐标分别为1,3.
在同一平面直角坐标系中作出函数y=x-4和y=x2-4x+3的图象(图略),要使函数f(x)的图象与x轴恰有2个交点,则只能有以下两种情形:①两个交点的横坐标分别为1,3,此时λ>4;②两个交点的横坐标分别为1,4,此时1<λ≤3.
综上,λ的取值范围为(1,3]∪(4,+∞).
14.解析 (1)当9≤t≤15时,p(t)=1 800>1 500,不满足题意,舍去.
当4≤t<9时,令1 800-15(9-t)2≤1 500,即t2-18t+61≥0,解得t≥9+2(舍去)或t≤9-2.
因为4≤t<9且t∈N,所以t=4.
所以发车时间间隔为4分钟.
(2)由题意得q(t)=
当4≤t<9时,q(t)≤-2+1 540=280,当且仅当90t=,即t=7时,等号成立.
当9≤t≤15时,q(t)≤-80=240.
因为280>240,所以当发车时间间隔为7分钟时,平均每趟快递车辆每分钟的净收益最大,最大净收益为280元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
