2025苏教版高中数学必修第一册同步练习题--6.3 对数函数(含解析)
文档属性
| 名称 | 2025苏教版高中数学必修第一册同步练习题--6.3 对数函数(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 486.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-23 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025苏教版高中数学必修第一册
6.3 对数函数
基础过关练
题组一 对数函数的概念及应用
1.(2024江苏淮安马坝高级中学阶段测试)下列函数中为对数函数的是( )
A.y=lo(-x) B.y=2log4(1-x)
C.y=ln x D.y=lox
2.(2024江苏扬州江都中学阶段检测)已知对数函数f(x)=(a2-3a+3)logax(a>0,且a≠1),则a的值是( )
A.1或2 B.1
C.2 D.任意的
3.已知f(x)为对数函数,f=-2,则f()= .
题组二 对数(型)函数的图象
4.为了得到函数f(x)=log2x的图象,只需将函数g(x)=log2的图象( )
A.向上平移3个单位长度
B.向下平移3个单位长度
C.向左平移3个单位长度
D.向右平移3个单位长度
5.当a取4个不同的值时,对数函数y=logax(a>0,且a≠1)的图象如图中曲线所示,已知a的值分别为,,,,则相应于曲线C1,C2,C3,C4的a的值依次是( )
A.,,,
B.,,,
C.,,,
D.,,,
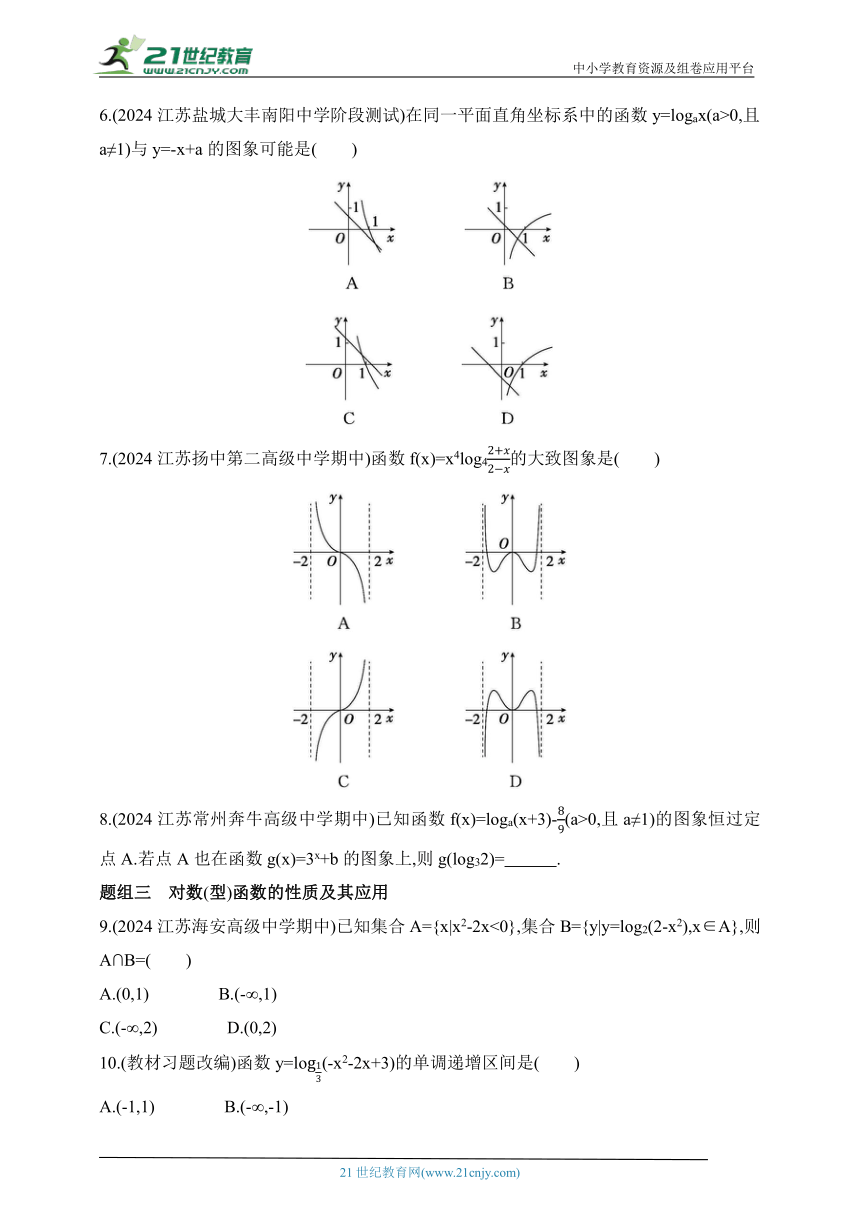
6.(2024江苏盐城大丰南阳中学阶段测试)在同一平面直角坐标系中的函数y=logax(a>0,且a≠1)与y=-x+a的图象可能是( )
7.(2024江苏扬中第二高级中学期中)函数f(x)=x4log4的大致图象是( )
8.(2024江苏常州奔牛高级中学期中)已知函数f(x)=loga(x+3)-(a>0,且a≠1)的图象恒过定点A.若点A也在函数g(x)=3x+b的图象上,则g(log32)= .
题组三 对数(型)函数的性质及其应用
9.(2024江苏海安高级中学期中)已知集合A={x|x2-2x<0},集合B={y|y=log2(2-x2),x∈A},则A∩B=( )
A.(0,1) B.(-∞,1)
C.(-∞,2) D.(0,2)
10.(教材习题改编)函数y=lo(-x2-2x+3)的单调递增区间是( )
A.(-1,1) B.(-∞,-1)
C.(1,3) D.(-1,+∞)
11.(2024江苏宿迁泗阳实验高级中学期末)已知正数a,b,c满足2 023a=2 024,2 024b=2 023,ec=2,则下列说法正确的是( )
A.logac>logbc B.logca>logcb
C.ac12.(2024山东临沂第一中学期中)已知g(x)为R上的偶函数,当x>0时,g(x)=x2+log2x,则g(-2)= .
13.已知函数f(x)=logax(a>0,且a≠1)在[1,4]上的最大值与最小值的和是2,则a的值为 .
14.(2022安徽合肥六中月考)已知函数f(x)=m+logax(a>0,且a≠1)的图象过点(9,4)和(1,2).
(1)求函数f(x)的解析式;
(2)若f(x)的定义域为[1,81],求y=[f(x)]2+f(x2)的最大值及y取最大值时x的值.
15.(2023江苏徐州侯集高级中学月考)已知函数f(x)=loga(2+3x)-loga(2-3x)(a>0,且a≠1).
(1)求函数f(x)的定义域;
(2)判断f(x)的奇偶性,并证明;
(3)当016.(2024江苏苏州学业测试)已知函数f(x)=log2log2.
(1)当x∈[2,8]时,求该函数的值域;
(2)若不等式f(x)≥mlog2x在x∈[4,16]上有解,求m的取值范围.
题组四 反函数
17.(2024福建福州期中)已知函数f(x)=log5x,g(x)是f(x)的反函数,则f(1)+g(1)=( )
A.10 B.8 C.5 D.2
18.(2024江苏盐城滨海中学期末)已知函数f(x)=,函数g(x)与f(x)的图象关于直线y=x对称,则[f(x)]2-f(x)+g(9)≥0的解集为( )
A.{x|x≥-log32} B.{x|x≤-log32}
C.{x|x≥log32} D.{x|x≤log32}
能力提升练
题组一 对数(型)函数的图象及其应用
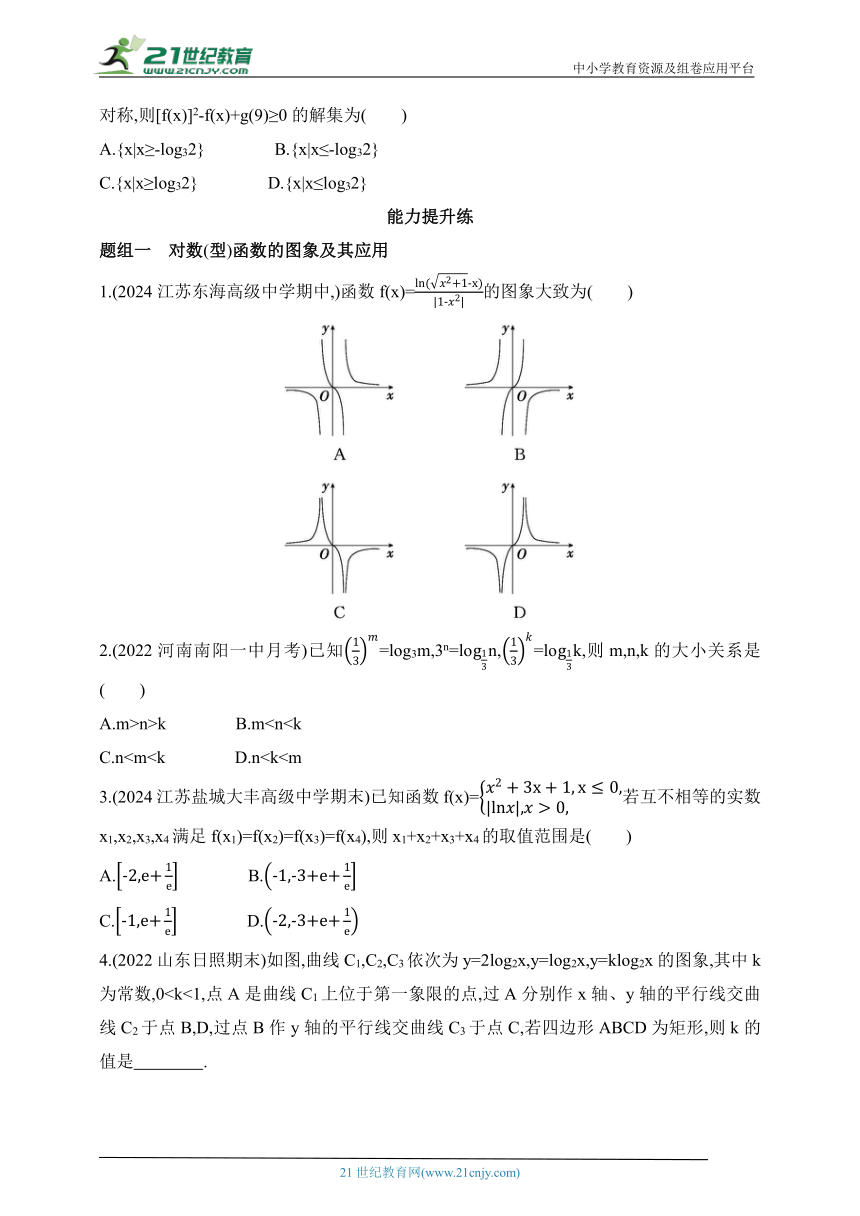
1.(2024江苏东海高级中学期中,)函数f(x)=的图象大致为( )
2.(2022河南南阳一中月考)已知=log3m,3n=lon,=lok,则m,n,k的大小关系是( )
A.m>n>k B.mC.n3.(2024江苏盐城大丰高级中学期末)已知函数f(x)=若互不相等的实数x1,x2,x3,x4满足f(x1)=f(x2)=f(x3)=f(x4),则x1+x2+x3+x4的取值范围是( )
A. B.
C. D.
4.(2022山东日照期末)如图,曲线C1,C2,C3依次为y=2log2x,y=log2x,y=klog2x的图象,其中k为常数,0题组二 对数(型)函数的性质及其应用
5.(2023江苏淮安中学期末,)设函数f(x)的定义域为(-1,3),则函数g(x)=的定义域为( )
A.(-2,1) B.(-2,0)∪(0,1)
C.(0,1) D.(-∞,0)∪(0,1)
6.(2024江苏泰州中学期中,)设a=160.3,b=log23,c=log34,则( )
A.a>b>c B.c>b>a C.a>c>b D.b>a>c
7.(多选题)(2024江苏南京联考)若函数f(x)=lg(x2+2ax-a),则下列说法正确的是( )
A.若a=0,则f(x)为偶函数
B.若f(x)的定义域为R,则-1C.若a=1,则f(x)的增区间为(-1,+∞)
D.若f(x)在(-1,0)上单调递减,则a≤0
8.(2024江苏淮安金湖中学期末)若不等式x2-loga(x+1)<2x-1在x∈上恒成立,则实数a的取值范围为( )
A. B.
C. D.
9.(2023江苏天星湖中学期中)已知定义域为R的奇函数f(x),当x>0时,f(x)=则f(2)+f(4)+f(6)+…+f(2 022)= .
10.(2024湖北咸宁期中,)已知函数f(x)=2 024x-2 024-x+log2 024(+x)+1 012,则关于x的不等式f(4x+1)+f(2x+1)-2 024<0的解集为 .
11.(2022山东潍坊期末)已知函数f(x)=log9(9x+1)+bx(b∈R)为偶函数.
(1)求b的值;
(2)求f(x)的最小值;
(3)若f(t(2x-2-x))12.(2023上海致远高级中学月考)已知a∈R,函数f(x)=log2.
(1)当a=1时,解不等式f(x)>1;
(2)若关于x的方程f(x)+log2x2 =0的解集中恰有一个元素,求a的值;
(3)设a>0,若对任意t∈,函数f(x)在[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.
13.(2024江苏苏州期末)已知t为实数,函数f(x)=2loga(2x-t-2),g(x)=logax,其中0(1)若函数φ(x)=g(ax+1)-kx是偶函数,求实数k的值;
(2)当x∈[1,4]时, f(x)的图象始终在g(x)的图象的下方,求t的取值范围;
(3)设t=4,当x∈[m,n]时,函数y=|f(x)|的值域为[0,2],若n-m的最小值为,求实数a的值.
答案与分层梯度式解析
6.3 对数函数
基础过关练
1.C 函数y=lo(-x),y=2log4(1-x)的真数不是自变量x,它们不是对数函数,函数y=ln x是对数函数,函数y=lox的底数含有参数a,而a的值不能保证a2+a是不等于1的正数.故选C.
2.C 由题意得a2-3a+3=1,∴a=2.故选C.
3.答案
解析 设f(x)=logax(a>0且a≠1),则loga=-2,所以=,所以a=,所以f(x)=x,
所以f()=log =log2()2=log2=.
4.A g(x)=log2=log2x-log28=log2x-3,所以只需将函数g(x)=log2的图象向上平移3个单位长度,即可得到函数f(x)=log2x的图象,故选A.
5.B 解法一:C1,C2对应的底数一定大于1,C3,C4对应的底数一定小于1,故排除C,D;对数函数的底数大于1时,底数越大,图象越靠近x轴;底数大于0且小于1时,底数越小,图象越靠近x轴,可得C1,C2,C3,C4对应的a的值依次为,,,.
解法二:过点(0,1)作平行于x轴的直线(图略),记其与C1,C2,C3,C4交点的坐标分别为(a1,1),(a2,1),(a3,1),(a4,1),易知a1,a2,a3,a4分别为各对数函数的底数,显然a1>a2>a3>a4,所以C1,C2,C3,C4的底数分别为,,,.
6.A 当0当a>1时,函数y=logax在(0,+∞)上单调递增,函数y=-x+a在R上单调递减,且当x=0时,y=a∈(1,+∞),故B,D错误.故选A.
7.C 令>0,得-2∴f(x)为奇函数,其图象关于原点对称,排除B,D;
f(1)=14×log4=log43>0,排除A.故选C.
8.答案 1
解析 令x+3=1,得x=-2,所以f(-2)=loga1-=-,所以A,将其代入g(x)=3x+b,得g(-2)=3-2+b=-,解得b=-1,所以g(x)=3x-1,
所以g(log32)=-1=2-1=1.
9.A A={x|x2-2x<0}=(0,2),结合对数函数的概念及x∈(0,2),得0<2-x2<2,故log2(2-x2)<1,
故B={y|y=log2(2-x2),x∈A}=(-∞,1),
所以A∩B=(0,1).故选A.
10.A 由题知,-x2-2x+3>0,解得-3令t=-x2-2x+3,则t>0,易知y=lot在(0,+∞)上单调递减,t=-x2-2x+3在(-1,1)上单调递减,在(-3,-1)上单调递增,
由复合函数“同增异减”的单调性法则破题关键可知,y=lo(-x2-2x+3)的单调递增区间是(-1,1).故选A.
11.D ∵2 023a=2 024,2 024b=2 023,ec=2,
∴a=log2 0232 024>1,0∴logac<0,logbc>0,∴logac∵0b,∴logcabc,ca12.答案 5
解析 因为g(x)为R上的偶函数,
所以g(-2)=g(2),又当x>0时,g(x)=x2+log2x,
所以g(-2)=g(2)=22+log22=4+1=5.
13.答案 2
解析 ①当a>1时, f(x)=logax在(0,+∞)上为增函数,所以f(x)=logax在[1,4]上的最大值为loga4,最小值为loga1=0,所以loga4+0=2,解得a=2;
②当014.解析 (1)由题意得所以
所以f(x)=2+log3x.
(2)由(1)知y=[f(x)]2+f(x2)=+2+log3x2 =+2+2log3x=+6log3x+6=-3.
因为函数f(x)的定义域为[1,81],
所以要使函数y=[f(x)]2+f(x2)有意义,
需满足所以1≤x≤9,所以0≤log3x≤2,
所以当log3x=2,即x=9时,y取得最大值,且ymax=22.
所以函数y=[f(x)]2+f(x2)的最大值为22,y取最大值时x的值为9.
15.解析 (1)由题意得解得-(2)函数f(x)为奇函数,证明如下:
由(1)知,函数f(x)的定义域为,关于原点对称,又f(-x)=loga(2-3x)-loga(2+3x)=-f(x),
所以函数f(x)为奇函数.
(3)因为016.解析 (1)f(x)=log2log2=(log2x-2)(log2x-1),
当x∈[2,8]时,log2x∈[1,3],
令log2x=t,t∈[1,3],则g(t)=(t-2)(t-1)=t2-3t+2,t∈[1,3],
易得y=t2-3t+2的图象开口向上,对称轴为直线t=,
结合g(t)的定义域及二次函数的性质可知,当t=时,g(t)取得最小值,为-,当t=3时,g(t)取得最大值,为2,
所以当x∈[2,8]时,函数f(x)的值域为.
(2)当x∈[4,16]时,log2x∈[2,4],
令log2x=n,n∈[2,4],
由f(x)≥mlog2x在x∈[4,16]上有解,得(n-2)(n-1)=n2-3n+2≥mn在n∈[2,4]上有解,即n+-3≥m在n∈[2,4]上有解,
令h(n)=n+-3,n∈[2,4],因为函数h(n)在n∈[2,4]上单调递增,所以当n=4时,h(n)取得最大值,为,
所以m的取值范围是.
17.C 因为函数f(x)=log5x,g(x)是f(x)的反函数,
所以g(x)=5x,故f(1)+g(1)=log51+51=5.
故选C.
18.B 因为g(x)与f(x)的图象关于直线y=x对称,
所以g(x)是f(x)的反函数,即g(x)=lox,
则g(9)=lo9=lo=-2,
将原不等式化为--2≥0,
令t= ,则t>0,t2-t-2≥0,
即(t-2)(t+1)≥0,解得t≥2 或t≤-1(舍),
所以3-x≥2,解得x≤-log32.故选B.
能力提升练
1.C 由已知得函数的定义域为{x|x≠±1},关于原点对称,
∵f(-x)==
=-=-f(x),∴f(x)为奇函数,
令x=,则f()=,
又0<-==<1,∴f()<0,故排除A,D;
令x=,则f===,其中0<<1,故f<0,故排除B.故选C.
2.D 在同一平面直角坐标系中画出y=,y=log3x,y=3x,y=lox的图象,如图所示:
根据图象知n3.B 不妨设x1y=x2+3x+1的图象的对称轴为直线x=-,则x1+x2=-3,
当x>0时,|ln x3|=ln x4,即-ln x3=ln x4,即ln x3+ln x4=ln(x3x4)=0,得x3x4=1,所以x4=,当|ln x|=1时,x=或x=e,则x3∈,
所以x1+x2+x3+x4=-3+x3+在上单调递减,
当x3=时,x1+x2+x3+x4=-3+e+,当x3=1时,x1+x2+x3+x4=-1,
所以x1+x2+x3+x4的取值范围是.
故选B.
4.答案
解析 设A(t,2log2t),其中t>1,设B(x,2log2t),D(t,y),则得所以B(t2,2log2t),D(t,log2t),则点C的坐标为(t2,log2t),
将点C的坐标代入函数y=klog2x的解析式,得log2t=klog2t2,∴2k=1,解得k=.
5.B 要使g(x)=有意义,
只需解得即-26.A 因为y=log2x在(0,+∞)上单调递增,且<3<4,所以log2因为y=log3x在(0,+∞)上单调递增,且3<4<,
所以log33因为y=4x在R上单调递增,
所以a=160.3=40.6>40.5=2,
故a>b>c.故选A.
7.ABD 当a=0时, f(x)=lg x2,其定义域是{x|x≠0},关于原点对称,又f(-x)=f(x),所以f(x)是偶函数,A正确;
当f(x)的定义域为R时,方程x2+2ax-a=0的判别式Δ=4a2+4a<0,解得-1当a=1时, f(x)=lg(x2+2x-1),由x2+2x-1>0得x<-1-或x>-1+,则y=x2+2x-1的图象开口向上,且在(-1+,+∞)上单调递增,又y=lg x在其定义域上单调递增,所以f(x)的增区间是(-1+,+∞),C错误;
y=lg x在定义域上单调递增,要想f(x)在(-1,0)上单调递减,则y=x2+2ax-a在(-1,0)上单调递减,且当x=0时,y≥0,所以解得a≤0,D正确.
故选ABD.
8.C 因为x2-loga(x+1)<2x-1在x∈上恒成立,
所以(x-1)2令g(x)=(x-1)2, f(x)=loga(x+1),
若00,显然不合题意;
当a>1时,画出函数f(x)与g(x)的图象,如图所示,
结合图象知,要想满足(x-1)2综上,实数a的取值范围是.故选C.
9.答案 0
解析 由题意得f(2)=f(-1)=-f(1)=1, f(4)=f(1)=-1, f(6)=f(3)=f(0)=0.
因为 x>, f(x)=f(x-3),所以 n∈N*, f(6n-4)=f(2)=1, f(6n-2)=f(1)=-1, f(6n)=f(3)=0,
所以f(2)+f(4)+f(6)+…+f(2 022)=337×[f(2)+f(4)+f(6)]=0.
10.答案
解析 设g(x)=2 024x-2 024-x+log2 024(+x),其定义域为R,关于原点对称,又g(-x)+g(x)=2 024-x-2 024x+log2 024(-x)+2 024x-2 024-x+log2 024(+x)=0,所以函数g(x)为奇函数,
因为y=2 024x-2 024-x,y=log2 024(+x)在R上均单调递增,所以g(x)在R上单调递增.
因为f(4x+1)+f(2x+1)-2 024<0,所以g(4x+1)+g(2x+1)<0,即g(4x+1)11.解析 (1)因为f(x)为偶函数,所以f(-x)=f(x),
所以log9(9-x+1)-bx=log9(9x+1)+bx,所以2bx=log9-log9(9x+1)=log99-x=-x,所以b=-.
(2)由(1)知, f(x)=log9(9x+1)-=log9(9x+1)-log9=log9=log9.
因为3x+≥2=2,所以log9≥log92(当且仅当x=0时,等号成立),
所以f(x)的最小值为log92.
(3)由(2)知, f(x)=log9,任取x1,x2∈(0,+∞),且x1因为x1,x2∈(0,+∞),且x1所以-<0,-1>0,>0,
所以<0,
所以+<+,
所以log9所以f(x)在(0,+∞)上为增函数,
又因为f(x)为偶函数,所以|t(2x-2-x)|<|22x+2-2x|,当x=0时,0<2,t∈R;
当x≠0时,|2x-2-x|>0,所以|t|<,
设u(x)===|2x-2-x|+≥2(当且仅当|2x-2-x|=时,等号成立),所以u(x)min=2,
所以|t|<2,所以-2综上所述,实数t的取值范围是-212.解析 (1)当a=1时, f(x)=log2,因为不等式f(x)>1,所以log2>1=log22,又y=log2x在(0,+∞)上单调递增,所以+1>2,即>1,所以0故原不等式的解集为(0,1).
(2)由f(x)+log2x2=0,得log2+log2x2=0,
即x2=1,所以ax2+x-1=0,
当a=0时,x-1=0,解得x=1,经验证,满足题意;
当a≠0时,①若Δ=1+4a=0,则a=-,所以-x2+x-1=0,解得x=2(二重根),经验证,满足题意;
②若Δ=1+4a>0,即a>-,则方程ax2+x-1=0有两个不相等的实数根,设为x1,x2,显然x1≠0,x2≠0,
因为x2=1,x2>0,
所以a+>0,即a+>0,a+>0,所以x1,x2都满足log2+log2x2=0,不满足题意.
综上,a=0或a=-.
(3)当a>0时,对任意t∈,函数f(x)在[t,t+1]上单调递减,所以log2-log2≤1,所以log2≤log2+1,
即at2+(a+1)t-1≥0对任意t∈恒成立,
因为a>0,所以y=at2+(a+1)t-1的图象开口向上,对称轴为直线t=-,且-<0,所以其在上单调递增,所以当t=时,y=at2+(a+1)t-1取得最小值,且最小值为a+(a+1)-1=a-,
所以a-≥0,即a≥,
所以实数a的取值范围是.
13.解析 (1)φ(x)=g(ax+1)-kx=loga(ax+1)-kx,
因为φ(x)=g(ax+1)-kx是偶函数,所以φ(-x)=φ(x)对任意x∈R恒成立,即loga(a-x+1)+kx=loga(ax+1)-kx对任意x∈R恒成立,
所以2kx=loga(ax+1)-loga(a-x+1)=loga=x,所以k=.
(2)设h(x)=f(x)-g(x)=2loga(2x-t-2)-logax,
因为当x∈[1,4]时, f(x)的图象始终在g(x)的图象的下方,
所以h(x)=2loga(2x-t-2)-logax<0在x∈[1,4]上恒成立,
即2loga(2x-t-2)因为0,
即t<2x--2在x∈[1,4]上恒成立,
设y=2x--2=2-,x∈[1,4],
所以当x=1时,ymin=-1,所以t<-1,即实数t的取值范围为(-∞,-1).
(3)因为t=4,所以y=|f(x)|=|2loga(2x-6)|,令2x-6>0,得x>3,
又0因为当x∈[m,n]时,函数y=|f(x)|的值域为[0,2],
所以3令|2loga(2x-6)|=2,可得loga(2x-6)=±1,解得x=或x=,
又因为-=>0,
所以->-,
所以n-m的最小值为-=,解得a=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025苏教版高中数学必修第一册
6.3 对数函数
基础过关练
题组一 对数函数的概念及应用
1.(2024江苏淮安马坝高级中学阶段测试)下列函数中为对数函数的是( )
A.y=lo(-x) B.y=2log4(1-x)
C.y=ln x D.y=lox
2.(2024江苏扬州江都中学阶段检测)已知对数函数f(x)=(a2-3a+3)logax(a>0,且a≠1),则a的值是( )
A.1或2 B.1
C.2 D.任意的
3.已知f(x)为对数函数,f=-2,则f()= .
题组二 对数(型)函数的图象
4.为了得到函数f(x)=log2x的图象,只需将函数g(x)=log2的图象( )
A.向上平移3个单位长度
B.向下平移3个单位长度
C.向左平移3个单位长度
D.向右平移3个单位长度
5.当a取4个不同的值时,对数函数y=logax(a>0,且a≠1)的图象如图中曲线所示,已知a的值分别为,,,,则相应于曲线C1,C2,C3,C4的a的值依次是( )
A.,,,
B.,,,
C.,,,
D.,,,
6.(2024江苏盐城大丰南阳中学阶段测试)在同一平面直角坐标系中的函数y=logax(a>0,且a≠1)与y=-x+a的图象可能是( )
7.(2024江苏扬中第二高级中学期中)函数f(x)=x4log4的大致图象是( )
8.(2024江苏常州奔牛高级中学期中)已知函数f(x)=loga(x+3)-(a>0,且a≠1)的图象恒过定点A.若点A也在函数g(x)=3x+b的图象上,则g(log32)= .
题组三 对数(型)函数的性质及其应用
9.(2024江苏海安高级中学期中)已知集合A={x|x2-2x<0},集合B={y|y=log2(2-x2),x∈A},则A∩B=( )
A.(0,1) B.(-∞,1)
C.(-∞,2) D.(0,2)
10.(教材习题改编)函数y=lo(-x2-2x+3)的单调递增区间是( )
A.(-1,1) B.(-∞,-1)
C.(1,3) D.(-1,+∞)
11.(2024江苏宿迁泗阳实验高级中学期末)已知正数a,b,c满足2 023a=2 024,2 024b=2 023,ec=2,则下列说法正确的是( )
A.logac>logbc B.logca>logcb
C.ac
13.已知函数f(x)=logax(a>0,且a≠1)在[1,4]上的最大值与最小值的和是2,则a的值为 .
14.(2022安徽合肥六中月考)已知函数f(x)=m+logax(a>0,且a≠1)的图象过点(9,4)和(1,2).
(1)求函数f(x)的解析式;
(2)若f(x)的定义域为[1,81],求y=[f(x)]2+f(x2)的最大值及y取最大值时x的值.
15.(2023江苏徐州侯集高级中学月考)已知函数f(x)=loga(2+3x)-loga(2-3x)(a>0,且a≠1).
(1)求函数f(x)的定义域;
(2)判断f(x)的奇偶性,并证明;
(3)当0
(1)当x∈[2,8]时,求该函数的值域;
(2)若不等式f(x)≥mlog2x在x∈[4,16]上有解,求m的取值范围.
题组四 反函数
17.(2024福建福州期中)已知函数f(x)=log5x,g(x)是f(x)的反函数,则f(1)+g(1)=( )
A.10 B.8 C.5 D.2
18.(2024江苏盐城滨海中学期末)已知函数f(x)=,函数g(x)与f(x)的图象关于直线y=x对称,则[f(x)]2-f(x)+g(9)≥0的解集为( )
A.{x|x≥-log32} B.{x|x≤-log32}
C.{x|x≥log32} D.{x|x≤log32}
能力提升练
题组一 对数(型)函数的图象及其应用
1.(2024江苏东海高级中学期中,)函数f(x)=的图象大致为( )
2.(2022河南南阳一中月考)已知=log3m,3n=lon,=lok,则m,n,k的大小关系是( )
A.m>n>k B.m
A. B.
C. D.
4.(2022山东日照期末)如图,曲线C1,C2,C3依次为y=2log2x,y=log2x,y=klog2x的图象,其中k为常数,0
5.(2023江苏淮安中学期末,)设函数f(x)的定义域为(-1,3),则函数g(x)=的定义域为( )
A.(-2,1) B.(-2,0)∪(0,1)
C.(0,1) D.(-∞,0)∪(0,1)
6.(2024江苏泰州中学期中,)设a=160.3,b=log23,c=log34,则( )
A.a>b>c B.c>b>a C.a>c>b D.b>a>c
7.(多选题)(2024江苏南京联考)若函数f(x)=lg(x2+2ax-a),则下列说法正确的是( )
A.若a=0,则f(x)为偶函数
B.若f(x)的定义域为R,则-1
D.若f(x)在(-1,0)上单调递减,则a≤0
8.(2024江苏淮安金湖中学期末)若不等式x2-loga(x+1)<2x-1在x∈上恒成立,则实数a的取值范围为( )
A. B.
C. D.
9.(2023江苏天星湖中学期中)已知定义域为R的奇函数f(x),当x>0时,f(x)=则f(2)+f(4)+f(6)+…+f(2 022)= .
10.(2024湖北咸宁期中,)已知函数f(x)=2 024x-2 024-x+log2 024(+x)+1 012,则关于x的不等式f(4x+1)+f(2x+1)-2 024<0的解集为 .
11.(2022山东潍坊期末)已知函数f(x)=log9(9x+1)+bx(b∈R)为偶函数.
(1)求b的值;
(2)求f(x)的最小值;
(3)若f(t(2x-2-x))
(1)当a=1时,解不等式f(x)>1;
(2)若关于x的方程f(x)+log2x2 =0的解集中恰有一个元素,求a的值;
(3)设a>0,若对任意t∈,函数f(x)在[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.
13.(2024江苏苏州期末)已知t为实数,函数f(x)=2loga(2x-t-2),g(x)=logax,其中0
(2)当x∈[1,4]时, f(x)的图象始终在g(x)的图象的下方,求t的取值范围;
(3)设t=4,当x∈[m,n]时,函数y=|f(x)|的值域为[0,2],若n-m的最小值为,求实数a的值.
答案与分层梯度式解析
6.3 对数函数
基础过关练
1.C 函数y=lo(-x),y=2log4(1-x)的真数不是自变量x,它们不是对数函数,函数y=ln x是对数函数,函数y=lox的底数含有参数a,而a的值不能保证a2+a是不等于1的正数.故选C.
2.C 由题意得a2-3a+3=1,∴a=2.故选C.
3.答案
解析 设f(x)=logax(a>0且a≠1),则loga=-2,所以=,所以a=,所以f(x)=x,
所以f()=log =log2()2=log2=.
4.A g(x)=log2=log2x-log28=log2x-3,所以只需将函数g(x)=log2的图象向上平移3个单位长度,即可得到函数f(x)=log2x的图象,故选A.
5.B 解法一:C1,C2对应的底数一定大于1,C3,C4对应的底数一定小于1,故排除C,D;对数函数的底数大于1时,底数越大,图象越靠近x轴;底数大于0且小于1时,底数越小,图象越靠近x轴,可得C1,C2,C3,C4对应的a的值依次为,,,.
解法二:过点(0,1)作平行于x轴的直线(图略),记其与C1,C2,C3,C4交点的坐标分别为(a1,1),(a2,1),(a3,1),(a4,1),易知a1,a2,a3,a4分别为各对数函数的底数,显然a1>a2>a3>a4,所以C1,C2,C3,C4的底数分别为,,,.
6.A 当0
7.C 令>0,得-2
f(1)=14×log4=log43>0,排除A.故选C.
8.答案 1
解析 令x+3=1,得x=-2,所以f(-2)=loga1-=-,所以A,将其代入g(x)=3x+b,得g(-2)=3-2+b=-,解得b=-1,所以g(x)=3x-1,
所以g(log32)=-1=2-1=1.
9.A A={x|x2-2x<0}=(0,2),结合对数函数的概念及x∈(0,2),得0<2-x2<2,故log2(2-x2)<1,
故B={y|y=log2(2-x2),x∈A}=(-∞,1),
所以A∩B=(0,1).故选A.
10.A 由题知,-x2-2x+3>0,解得-3
由复合函数“同增异减”的单调性法则破题关键可知,y=lo(-x2-2x+3)的单调递增区间是(-1,1).故选A.
11.D ∵2 023a=2 024,2 024b=2 023,ec=2,
∴a=log2 0232 024>1,0
解析 因为g(x)为R上的偶函数,
所以g(-2)=g(2),又当x>0时,g(x)=x2+log2x,
所以g(-2)=g(2)=22+log22=4+1=5.
13.答案 2
解析 ①当a>1时, f(x)=logax在(0,+∞)上为增函数,所以f(x)=logax在[1,4]上的最大值为loga4,最小值为loga1=0,所以loga4+0=2,解得a=2;
②当0
所以f(x)=2+log3x.
(2)由(1)知y=[f(x)]2+f(x2)=+2+log3x2 =+2+2log3x=+6log3x+6=-3.
因为函数f(x)的定义域为[1,81],
所以要使函数y=[f(x)]2+f(x2)有意义,
需满足所以1≤x≤9,所以0≤log3x≤2,
所以当log3x=2,即x=9时,y取得最大值,且ymax=22.
所以函数y=[f(x)]2+f(x2)的最大值为22,y取最大值时x的值为9.
15.解析 (1)由题意得解得-
由(1)知,函数f(x)的定义域为,关于原点对称,又f(-x)=loga(2-3x)-loga(2+3x)=-f(x),
所以函数f(x)为奇函数.
(3)因为0
当x∈[2,8]时,log2x∈[1,3],
令log2x=t,t∈[1,3],则g(t)=(t-2)(t-1)=t2-3t+2,t∈[1,3],
易得y=t2-3t+2的图象开口向上,对称轴为直线t=,
结合g(t)的定义域及二次函数的性质可知,当t=时,g(t)取得最小值,为-,当t=3时,g(t)取得最大值,为2,
所以当x∈[2,8]时,函数f(x)的值域为.
(2)当x∈[4,16]时,log2x∈[2,4],
令log2x=n,n∈[2,4],
由f(x)≥mlog2x在x∈[4,16]上有解,得(n-2)(n-1)=n2-3n+2≥mn在n∈[2,4]上有解,即n+-3≥m在n∈[2,4]上有解,
令h(n)=n+-3,n∈[2,4],因为函数h(n)在n∈[2,4]上单调递增,所以当n=4时,h(n)取得最大值,为,
所以m的取值范围是.
17.C 因为函数f(x)=log5x,g(x)是f(x)的反函数,
所以g(x)=5x,故f(1)+g(1)=log51+51=5.
故选C.
18.B 因为g(x)与f(x)的图象关于直线y=x对称,
所以g(x)是f(x)的反函数,即g(x)=lox,
则g(9)=lo9=lo=-2,
将原不等式化为--2≥0,
令t= ,则t>0,t2-t-2≥0,
即(t-2)(t+1)≥0,解得t≥2 或t≤-1(舍),
所以3-x≥2,解得x≤-log32.故选B.
能力提升练
1.C 由已知得函数的定义域为{x|x≠±1},关于原点对称,
∵f(-x)==
=-=-f(x),∴f(x)为奇函数,
令x=,则f()=,
又0<-==<1,∴f()<0,故排除A,D;
令x=,则f===,其中0<<1,故f<0,故排除B.故选C.
2.D 在同一平面直角坐标系中画出y=,y=log3x,y=3x,y=lox的图象,如图所示:
根据图象知n
当x>0时,|ln x3|=ln x4,即-ln x3=ln x4,即ln x3+ln x4=ln(x3x4)=0,得x3x4=1,所以x4=,当|ln x|=1时,x=或x=e,则x3∈,
所以x1+x2+x3+x4=-3+x3+在上单调递减,
当x3=时,x1+x2+x3+x4=-3+e+,当x3=1时,x1+x2+x3+x4=-1,
所以x1+x2+x3+x4的取值范围是.
故选B.
4.答案
解析 设A(t,2log2t),其中t>1,设B(x,2log2t),D(t,y),则得所以B(t2,2log2t),D(t,log2t),则点C的坐标为(t2,log2t),
将点C的坐标代入函数y=klog2x的解析式,得log2t=klog2t2,∴2k=1,解得k=.
5.B 要使g(x)=有意义,
只需解得即-2
所以log33
所以a=160.3=40.6>40.5=2,
故a>b>c.故选A.
7.ABD 当a=0时, f(x)=lg x2,其定义域是{x|x≠0},关于原点对称,又f(-x)=f(x),所以f(x)是偶函数,A正确;
当f(x)的定义域为R时,方程x2+2ax-a=0的判别式Δ=4a2+4a<0,解得-1
y=lg x在定义域上单调递增,要想f(x)在(-1,0)上单调递减,则y=x2+2ax-a在(-1,0)上单调递减,且当x=0时,y≥0,所以解得a≤0,D正确.
故选ABD.
8.C 因为x2-loga(x+1)<2x-1在x∈上恒成立,
所以(x-1)2
若0
当a>1时,画出函数f(x)与g(x)的图象,如图所示,
结合图象知,要想满足(x-1)2
9.答案 0
解析 由题意得f(2)=f(-1)=-f(1)=1, f(4)=f(1)=-1, f(6)=f(3)=f(0)=0.
因为 x>, f(x)=f(x-3),所以 n∈N*, f(6n-4)=f(2)=1, f(6n-2)=f(1)=-1, f(6n)=f(3)=0,
所以f(2)+f(4)+f(6)+…+f(2 022)=337×[f(2)+f(4)+f(6)]=0.
10.答案
解析 设g(x)=2 024x-2 024-x+log2 024(+x),其定义域为R,关于原点对称,又g(-x)+g(x)=2 024-x-2 024x+log2 024(-x)+2 024x-2 024-x+log2 024(+x)=0,所以函数g(x)为奇函数,
因为y=2 024x-2 024-x,y=log2 024(+x)在R上均单调递增,所以g(x)在R上单调递增.
因为f(4x+1)+f(2x+1)-2 024<0,所以g(4x+1)+g(2x+1)<0,即g(4x+1)
所以log9(9-x+1)-bx=log9(9x+1)+bx,所以2bx=log9-log9(9x+1)=log99-x=-x,所以b=-.
(2)由(1)知, f(x)=log9(9x+1)-=log9(9x+1)-log9=log9=log9.
因为3x+≥2=2,所以log9≥log92(当且仅当x=0时,等号成立),
所以f(x)的最小值为log92.
(3)由(2)知, f(x)=log9,任取x1,x2∈(0,+∞),且x1
所以<0,
所以+<+,
所以log9
又因为f(x)为偶函数,所以|t(2x-2-x)|<|22x+2-2x|,当x=0时,0<2,t∈R;
当x≠0时,|2x-2-x|>0,所以|t|<,
设u(x)===|2x-2-x|+≥2(当且仅当|2x-2-x|=时,等号成立),所以u(x)min=2,
所以|t|<2,所以-2
(2)由f(x)+log2x2=0,得log2+log2x2=0,
即x2=1,所以ax2+x-1=0,
当a=0时,x-1=0,解得x=1,经验证,满足题意;
当a≠0时,①若Δ=1+4a=0,则a=-,所以-x2+x-1=0,解得x=2(二重根),经验证,满足题意;
②若Δ=1+4a>0,即a>-,则方程ax2+x-1=0有两个不相等的实数根,设为x1,x2,显然x1≠0,x2≠0,
因为x2=1,x2>0,
所以a+>0,即a+>0,a+>0,所以x1,x2都满足log2+log2x2=0,不满足题意.
综上,a=0或a=-.
(3)当a>0时,对任意t∈,函数f(x)在[t,t+1]上单调递减,所以log2-log2≤1,所以log2≤log2+1,
即at2+(a+1)t-1≥0对任意t∈恒成立,
因为a>0,所以y=at2+(a+1)t-1的图象开口向上,对称轴为直线t=-,且-<0,所以其在上单调递增,所以当t=时,y=at2+(a+1)t-1取得最小值,且最小值为a+(a+1)-1=a-,
所以a-≥0,即a≥,
所以实数a的取值范围是.
13.解析 (1)φ(x)=g(ax+1)-kx=loga(ax+1)-kx,
因为φ(x)=g(ax+1)-kx是偶函数,所以φ(-x)=φ(x)对任意x∈R恒成立,即loga(a-x+1)+kx=loga(ax+1)-kx对任意x∈R恒成立,
所以2kx=loga(ax+1)-loga(a-x+1)=loga=x,所以k=.
(2)设h(x)=f(x)-g(x)=2loga(2x-t-2)-logax,
因为当x∈[1,4]时, f(x)的图象始终在g(x)的图象的下方,
所以h(x)=2loga(2x-t-2)-logax<0在x∈[1,4]上恒成立,
即2loga(2x-t-2)
即t<2x--2在x∈[1,4]上恒成立,
设y=2x--2=2-,x∈[1,4],
所以当x=1时,ymin=-1,所以t<-1,即实数t的取值范围为(-∞,-1).
(3)因为t=4,所以y=|f(x)|=|2loga(2x-6)|,令2x-6>0,得x>3,
又0
所以3
又因为-=>0,
所以->-,
所以n-m的最小值为-=,解得a=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
