2025苏教版高中数学必修第一册同步练习题--第8章 函数应用复习提升(含解析)
文档属性
| 名称 | 2025苏教版高中数学必修第一册同步练习题--第8章 函数应用复习提升(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 416.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-23 18:14:40 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025苏教版高中数学必修第一册
本章复习提升
易混易错练
易错点1 忽视函数零点存在定理的使用条件致错
1.对于函数f(x),若f(-1)f(3)<0,则( )
A.方程f(x)=0一定有实数解
B.方程f(x)=0一定无实数解
C.方程f(x)=0一定有两个实数解
D.方程f(x)=0可能无实数解
2.设f(x)在区间[a,b]上是连续的单调函数,且f(a)f(b)<0,则方程f(x)=0在[a,b]内( )
A.至少有一实根 B.至多有一实根
C.没有实根 D.必有唯一实根
易错点2 函数图象画不准确致错
3.(2023江苏南京金陵中学期中)已知函数f(x)=若f(x)-a=0有3个不同的实数根,则实数a的取值范围是( )
A.0C.04.(2022江苏盛泽中学月考)已知函数f(x)=若关于x的函数y=[f(x)]2+2bf(x)+2b+1有6个不同的零点,则实数b的取值范围是( )
A. B.(-1,0)
C. D.
5.(2023上海普陀期中)设函数f(x)=函数g(x)=则方程f(x)=g(x)的解的个数为 .
易错点3 求参数的取值范围时考虑不全面致错
6.(2023湖南湘潭一中期末)已知函数f(x)=ax2-x+a,“函数f(x)在(0,2)上有两个不相等的零点”是“A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
7. (2024北京期末)已知函数f(x)=若函数y=f(x)-2有且仅有2个不同的零点,则实数a的取值范围是 .
8.已知函数f(x)=(log2x)2+4log2x+m,x∈,m为常数.
(1)设函数f(x)存在大于1的零点,求实数m的取值范围;
(2)设函数f(x)有两个互异的零点α,β,求实数m的取值范围,并求αβ的值.
思想方法练
一、转化与化归思想在函数零点问题中的应用
1. (2024天津期末)若定义在R上的偶函数f(x)满足f(x+2)=f(x),且当x∈[0,1]时, f(x)=x,则函数y=f(x)-log6|x|的零点个数是 ( )
A.6 B.10
C.14 D.18
2.(2023江苏无锡期末)已知函数f(x)=若关于x的方程f(x)=a(a∈R)有3个不同的实数解,则实数a的取值范围是( )
A.[1,5) B.(0,1)∪{5}
C.(0,1] D.(0,1)
3.已知函数f(x)=x+2x,g(x)=x+ln x,h(x)=x--1的零点分别为x1,x2,x3,则x1,x2,x3的大小关系是 .(用“<”连接)
二、分类讨论思想在函数零点问题中的应用
4. (2024江苏常州期中)已知关于x的方程2kx2-2x-5k-1=0的两个实数根一个小于1,另一个大于1,则实数k的取值范围是( )
A.(0,+∞)
B.(-1,0)
C.(-∞,-1)
D.(-∞,-1)∪(0,+∞)
5.(2023江苏南京二十九中月考)已知函数f(x)=-x2+ax-(a-1)2(a<1),g(x)=ln x,若h(x)=在(0,+∞)上有三个零点,则实数a的取值范围为( )
A. B.
C.(0,1) D.
6.(2022福建龙岩期末)若函数f(x)=ex+ln(x-a)在(0,+∞)上存在零点,则实数a的取值范围是 .
7. (2024北京延庆期末)已知函数f(x)=(3x+1)-mx,m∈R.
(1)当m=0时,若f(x)=-2,求x的值;
(2)若f(x)是偶函数,求出m的值;
(3)当m=-时,求出方程f(x)=b的根的个数.
答案与分层梯度式解析
本章复习提升
易混易错练
1.D 因为f(x)的图象不一定是连续不断的,所以方程f(x)=0可能无实数解.
2.D 由题意知函数f(x)的图象在[a,b]内与x轴只有一个交点,即方程f(x)=0在[a,b]内只有一个实根.
易错警示 函数零点存在定理成立的条件有两个:①函数图象在所给的闭区间上是一条连续不断的曲线;②区间端点处的函数值异号.
3.C 作出函数f(x)的图象,如图所示:
由图可知,实数a的取值范围为04.A 作出函数f(x)的图象,如图所示:
令f(x)=t(0令g(t)=t2+2bt+2b+1,则函数g(t)有2个不同的零点,
由图知,t1,t2均在区间(0,1)内,t1,t2各对应3个根,
又函数g(t)的图象开口向上,
所以
解得-5.答案 11
解析 当x<0时,在同一平面直角坐标系中作出函数f(x)和g(x)的图象,如图1所示.
图1
由图可知,y=f(x)与y=g(x)的图象在(-∞,0)上有9个交点.
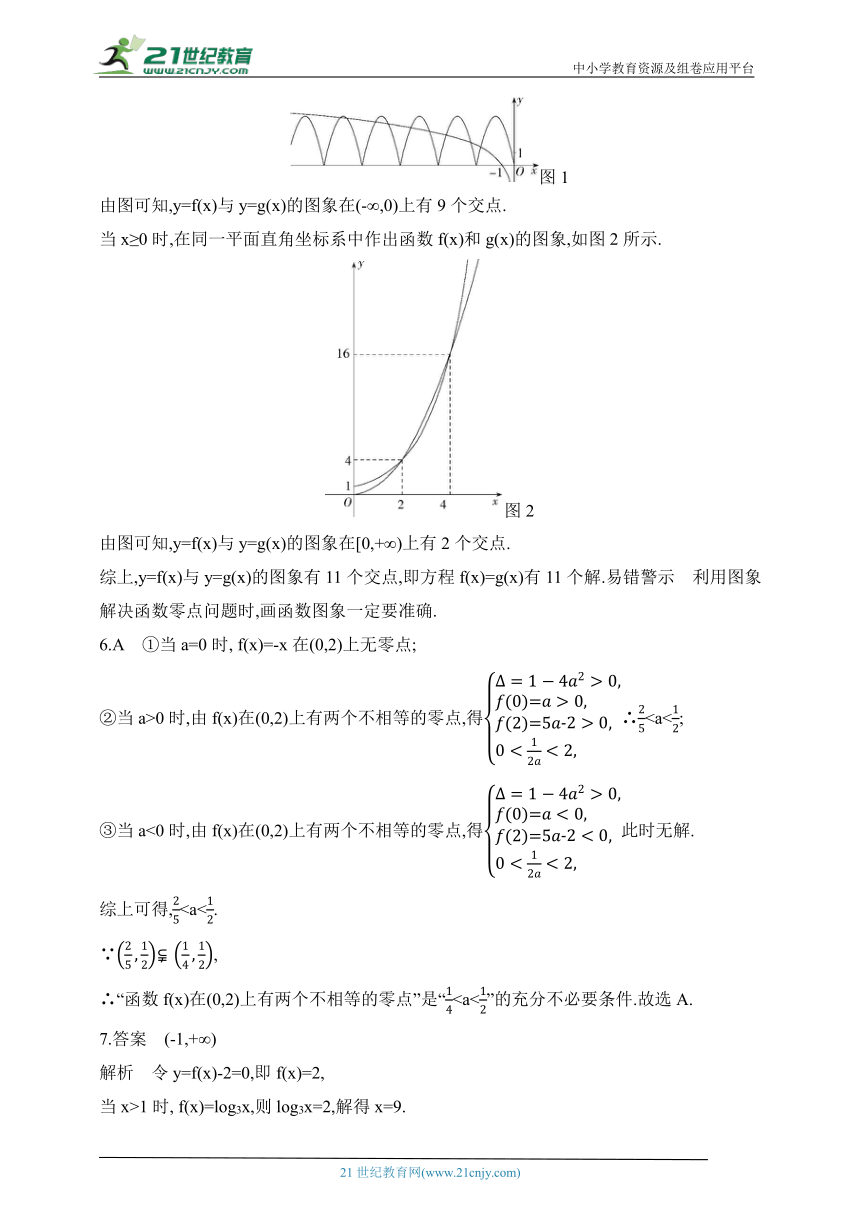
当x≥0时,在同一平面直角坐标系中作出函数f(x)和g(x)的图象,如图2所示.
图2
由图可知,y=f(x)与y=g(x)的图象在[0,+∞)上有2个交点.
综上,y=f(x)与y=g(x)的图象有11个交点,即方程f(x)=g(x)有11个解.易错警示 利用图象解决函数零点问题时,画函数图象一定要准确.
6.A ①当a=0时, f(x)=-x在(0,2)上无零点;
②当a>0时,由f(x)在(0,2)上有两个不相等的零点,得∴③当a<0时,由f(x)在(0,2)上有两个不相等的零点,得此时无解.
综上可得,∵ ,
∴“函数f(x)在(0,2)上有两个不相等的零点”是“7.答案 (-1,+∞)
解析 令y=f(x)-2=0,即f(x)=2,
当x>1时, f(x)=log3x,则log3x=2,解得x=9.
当x≤1时, f(x)=x2-ax,则x2-ax=2,即x2-ax-2=0,
由题意可知,方程x2-ax-2=0在(-∞,1]内只有一个根,
令g(x)=x2-ax-2,则g(x)的图象开口向上,且g(0)=-2<0,可得g(1)=1-a-2<0,解得a>-1,
所以实数a的取值范围是(-1,+∞).
8.解析 (1)令a=log2x,x∈,
则原函数可转化为y=a2+4a+m,a∈[-3,2].
因为函数f(x)存在大于1的零点,
所以方程a2+4a+m=0在(0,2]上存在实根.
由a2+4a+m=0,得m=-a2-4a,a∈(0,2],
所以m∈[-12,0).
故实数m的取值范围为[-12,0).
(2)令t=log2x,x∈,则原函数可转化为g(t)=t2+4t+m,t∈[-3,2].
若函数f(x)有两个互异的零点α,β,
则函数g(t)=t2+4t+m在[-3,2]上有两个互异的零点t1,t2,其中t1=log2α,t2=log2β,
所以解得3≤m<4,
所以实数m的取值范围为[3,4).
因为t1+t2=-4,所以log2α+log2β=-4,
所以log2(αβ)=-4,
所以αβ=2-4=.
思想方法练
1.B 因为 f(x+2)=f(x),所以f(x)是周期为2的周期函数,
由于f(x)是偶函数,且当x∈[0,1]时, f(x)=x,
所以当x∈[-1,0]时, f(x)=-x.
将函数零点问题转化为两个函数图象的交点问题.
在同一平面直角坐标系中画出y=f(x)与y=log6|x|的图象如图所示,
由图可知,两个函数图象有10个交点,
所以函数y=f(x)-log6|x|的零点个数是10.
故选B.
2.B 方程f(x)=a(a∈R)有3个不同的实数解,即函数y=f(x)的图象与直线y=a有3个不同的交点.
作出函数y=f(x)的图象与直线y=a,如图所示.
由图可知,实数a的取值范围为(0,1)∪{5}.故选B.
3.答案 x1解析 将函数零点问题转化为函数图象的交点问题.
令x+2x=0,得2x=-x.令x+ln x=0,得ln x=-x.
在同一平面直角坐标系中作出y=2x,y=ln x,y=-x的图象,如图所示:
由图可知x1<0令h(x)=x--1=0,则()2--1=0,
解得=(负值舍去),所以x3=>1.
综上,x1思想方法 本章中,判断函数零点的个数、与零点有关的参数等问题中都会用到转化与化归思想,画出函数图象,图象与x轴交点的横坐标就是函数的零点,两图象交点的个数就是函数零点的个数.
4.D 记f(x)=2kx2-2x-5k-1,由题意可知函数f(x)有两个零点,所以k≠0,
根据二次函数表达式中二次项的系数与0的大小关系进行分类讨论.
当k>0时,f(x)=2kx2-2x-5k-1的图象开口向上,
要想f(x)的两个零点一个大于1,另一个小于1,只需f(1)=2k-2-5k-1<0,解得k>-1,所以k>0;
当k<0时,f(x)=2kx2-2x-5k-1的图象开口向下,
要想f(x)的两个零点一个大于1,另一个小于1,只需f(1)=2k-2-5k-1>0,解得k<-1,所以k<-1.
综上所述,实数k的取值范围是(-∞,-1)∪(0,+∞).
5.A 结合g(x)的零点,分x=1,01进行讨论,从而确定1为h(x)的一个零点, f(x)在(0,1)上有两个零点.
①当x=1时,g(1)=0,所以g(x)的一个零点为1.
因为f(1)=a-1-(a-1)2,a<1,所以f(1)<0,所以h(1)=g(1)=0,所以1为h(x)的一个零点.
②当x>1时,g(x)>0, f(x)<0,则h(x)≥g(x)>0,所以h(x)在(1,+∞)上无零点.
③当0所以函数f(x)在(0,1)上有两个零点,即函数h(x)在(0,1)上有两个零点,所以h(x)=f(x)=-x2+ax-(a-1)2(00,解得a>,又a<1,所以6.答案
解析 令f(x)=ex+ln(x-a)=0,则-ex=ln(x-a),
若f(x)在(0,+∞)上存在零点,则函数y=-ex与y=ln(x-a)的图象在(0,+∞)上有交点,
易知y=-ex在(0,+∞)上单调递减,且当x=0时,y=-1;y=ln(x-a)在(a,+∞)上单调递增.
a的大小影响函数图象的相对位置,故需分情况讨论并求解.
当a≥0时,易知两函数图象在(0,+∞)上必有交点,满足题意;
当a<0时,如图所示,
只需ln(-a)<-1,所以-综上所述,实数a的取值范围是.
7.解析 (1)当m=0时, f(x)=(3x+1)=-2,所以3x+1==9,所以x=log38.
(2)若f(x)是偶函数,则f(-x)=f(x),所以(3-x+1)+mx=(3x+1)-mx,即 2mx=(3x+1)-(3-x+1)==-x,所以m=-.
(3)当m=-时, f(x)=(3x+1)+x=(3x+1)+==()x+,
令g(x)=()x+,任取x1,x2∈(0,+∞),且x1因为01,(>1,(<(,所以(·(>1,(-(<0,
所以g(x1)-g(x2)<0,
即g(x)=()x+在(0,+∞)上单调递增,
由复合函数的单调性可知f(x)在(0,+∞)上单调递减,
又由(2)知,当m=-时, f(x)是偶函数,
所以f(x)在(-∞,0)上单调递增,
则f(x)≤f(0)=-log32,
讨论b与-log32的大小关系,进而确定方程f(x)=b的根的个数.
当b>-log32时,方程f(x)=b没有实数根;
当b=-log32时,方程f(x)=b有且仅有1个实数根;
当 b<-log32时,取-2b∈(0,+∞),则f(-2b)==(3-b+3b)<3-b=b,
所以当x∈(0,-2b)时, f(0)=-log32>b, f(-2b)故由函数零点存在定理可知,当x∈(0,-2b)时, f(x)=b有1个实数根,
所以b<-log32时,方程f(x)=b有2个实数根.
综上所述,当b>-log32时,方程没有实数根;
当b=-log32时,方程有且仅有1个实数根;
当 b<-log32时,方程有2个实数根.
思想方法 在本章中,分类讨论思想主要用于解决函数零点及分段函数问题,主要体现在以下几个方面:(1)根据零点在不同的区间分情况讨论,求出零点;(2)根据函数在不同区间的取值讨论函数的解析式及对应性质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025苏教版高中数学必修第一册
本章复习提升
易混易错练
易错点1 忽视函数零点存在定理的使用条件致错
1.对于函数f(x),若f(-1)f(3)<0,则( )
A.方程f(x)=0一定有实数解
B.方程f(x)=0一定无实数解
C.方程f(x)=0一定有两个实数解
D.方程f(x)=0可能无实数解
2.设f(x)在区间[a,b]上是连续的单调函数,且f(a)f(b)<0,则方程f(x)=0在[a,b]内( )
A.至少有一实根 B.至多有一实根
C.没有实根 D.必有唯一实根
易错点2 函数图象画不准确致错
3.(2023江苏南京金陵中学期中)已知函数f(x)=若f(x)-a=0有3个不同的实数根,则实数a的取值范围是( )
A.0
A. B.(-1,0)
C. D.
5.(2023上海普陀期中)设函数f(x)=函数g(x)=则方程f(x)=g(x)的解的个数为 .
易错点3 求参数的取值范围时考虑不全面致错
6.(2023湖南湘潭一中期末)已知函数f(x)=ax2-x+a,“函数f(x)在(0,2)上有两个不相等的零点”是“
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
7. (2024北京期末)已知函数f(x)=若函数y=f(x)-2有且仅有2个不同的零点,则实数a的取值范围是 .
8.已知函数f(x)=(log2x)2+4log2x+m,x∈,m为常数.
(1)设函数f(x)存在大于1的零点,求实数m的取值范围;
(2)设函数f(x)有两个互异的零点α,β,求实数m的取值范围,并求αβ的值.
思想方法练
一、转化与化归思想在函数零点问题中的应用
1. (2024天津期末)若定义在R上的偶函数f(x)满足f(x+2)=f(x),且当x∈[0,1]时, f(x)=x,则函数y=f(x)-log6|x|的零点个数是 ( )
A.6 B.10
C.14 D.18
2.(2023江苏无锡期末)已知函数f(x)=若关于x的方程f(x)=a(a∈R)有3个不同的实数解,则实数a的取值范围是( )
A.[1,5) B.(0,1)∪{5}
C.(0,1] D.(0,1)
3.已知函数f(x)=x+2x,g(x)=x+ln x,h(x)=x--1的零点分别为x1,x2,x3,则x1,x2,x3的大小关系是 .(用“<”连接)
二、分类讨论思想在函数零点问题中的应用
4. (2024江苏常州期中)已知关于x的方程2kx2-2x-5k-1=0的两个实数根一个小于1,另一个大于1,则实数k的取值范围是( )
A.(0,+∞)
B.(-1,0)
C.(-∞,-1)
D.(-∞,-1)∪(0,+∞)
5.(2023江苏南京二十九中月考)已知函数f(x)=-x2+ax-(a-1)2(a<1),g(x)=ln x,若h(x)=在(0,+∞)上有三个零点,则实数a的取值范围为( )
A. B.
C.(0,1) D.
6.(2022福建龙岩期末)若函数f(x)=ex+ln(x-a)在(0,+∞)上存在零点,则实数a的取值范围是 .
7. (2024北京延庆期末)已知函数f(x)=(3x+1)-mx,m∈R.
(1)当m=0时,若f(x)=-2,求x的值;
(2)若f(x)是偶函数,求出m的值;
(3)当m=-时,求出方程f(x)=b的根的个数.
答案与分层梯度式解析
本章复习提升
易混易错练
1.D 因为f(x)的图象不一定是连续不断的,所以方程f(x)=0可能无实数解.
2.D 由题意知函数f(x)的图象在[a,b]内与x轴只有一个交点,即方程f(x)=0在[a,b]内只有一个实根.
易错警示 函数零点存在定理成立的条件有两个:①函数图象在所给的闭区间上是一条连续不断的曲线;②区间端点处的函数值异号.
3.C 作出函数f(x)的图象,如图所示:
由图可知,实数a的取值范围为0
令f(x)=t(0
由图知,t1,t2均在区间(0,1)内,t1,t2各对应3个根,
又函数g(t)的图象开口向上,
所以
解得-
解析 当x<0时,在同一平面直角坐标系中作出函数f(x)和g(x)的图象,如图1所示.
图1
由图可知,y=f(x)与y=g(x)的图象在(-∞,0)上有9个交点.
当x≥0时,在同一平面直角坐标系中作出函数f(x)和g(x)的图象,如图2所示.
图2
由图可知,y=f(x)与y=g(x)的图象在[0,+∞)上有2个交点.
综上,y=f(x)与y=g(x)的图象有11个交点,即方程f(x)=g(x)有11个解.易错警示 利用图象解决函数零点问题时,画函数图象一定要准确.
6.A ①当a=0时, f(x)=-x在(0,2)上无零点;
②当a>0时,由f(x)在(0,2)上有两个不相等的零点,得∴
综上可得,
∴“函数f(x)在(0,2)上有两个不相等的零点”是“
解析 令y=f(x)-2=0,即f(x)=2,
当x>1时, f(x)=log3x,则log3x=2,解得x=9.
当x≤1时, f(x)=x2-ax,则x2-ax=2,即x2-ax-2=0,
由题意可知,方程x2-ax-2=0在(-∞,1]内只有一个根,
令g(x)=x2-ax-2,则g(x)的图象开口向上,且g(0)=-2<0,可得g(1)=1-a-2<0,解得a>-1,
所以实数a的取值范围是(-1,+∞).
8.解析 (1)令a=log2x,x∈,
则原函数可转化为y=a2+4a+m,a∈[-3,2].
因为函数f(x)存在大于1的零点,
所以方程a2+4a+m=0在(0,2]上存在实根.
由a2+4a+m=0,得m=-a2-4a,a∈(0,2],
所以m∈[-12,0).
故实数m的取值范围为[-12,0).
(2)令t=log2x,x∈,则原函数可转化为g(t)=t2+4t+m,t∈[-3,2].
若函数f(x)有两个互异的零点α,β,
则函数g(t)=t2+4t+m在[-3,2]上有两个互异的零点t1,t2,其中t1=log2α,t2=log2β,
所以解得3≤m<4,
所以实数m的取值范围为[3,4).
因为t1+t2=-4,所以log2α+log2β=-4,
所以log2(αβ)=-4,
所以αβ=2-4=.
思想方法练
1.B 因为 f(x+2)=f(x),所以f(x)是周期为2的周期函数,
由于f(x)是偶函数,且当x∈[0,1]时, f(x)=x,
所以当x∈[-1,0]时, f(x)=-x.
将函数零点问题转化为两个函数图象的交点问题.
在同一平面直角坐标系中画出y=f(x)与y=log6|x|的图象如图所示,
由图可知,两个函数图象有10个交点,
所以函数y=f(x)-log6|x|的零点个数是10.
故选B.
2.B 方程f(x)=a(a∈R)有3个不同的实数解,即函数y=f(x)的图象与直线y=a有3个不同的交点.
作出函数y=f(x)的图象与直线y=a,如图所示.
由图可知,实数a的取值范围为(0,1)∪{5}.故选B.
3.答案 x1
令x+2x=0,得2x=-x.令x+ln x=0,得ln x=-x.
在同一平面直角坐标系中作出y=2x,y=ln x,y=-x的图象,如图所示:
由图可知x1<0
解得=(负值舍去),所以x3=>1.
综上,x1
4.D 记f(x)=2kx2-2x-5k-1,由题意可知函数f(x)有两个零点,所以k≠0,
根据二次函数表达式中二次项的系数与0的大小关系进行分类讨论.
当k>0时,f(x)=2kx2-2x-5k-1的图象开口向上,
要想f(x)的两个零点一个大于1,另一个小于1,只需f(1)=2k-2-5k-1<0,解得k>-1,所以k>0;
当k<0时,f(x)=2kx2-2x-5k-1的图象开口向下,
要想f(x)的两个零点一个大于1,另一个小于1,只需f(1)=2k-2-5k-1>0,解得k<-1,所以k<-1.
综上所述,实数k的取值范围是(-∞,-1)∪(0,+∞).
5.A 结合g(x)的零点,分x=1,0
①当x=1时,g(1)=0,所以g(x)的一个零点为1.
因为f(1)=a-1-(a-1)2,a<1,所以f(1)<0,所以h(1)=g(1)=0,所以1为h(x)的一个零点.
②当x>1时,g(x)>0, f(x)<0,则h(x)≥g(x)>0,所以h(x)在(1,+∞)上无零点.
③当0
解析 令f(x)=ex+ln(x-a)=0,则-ex=ln(x-a),
若f(x)在(0,+∞)上存在零点,则函数y=-ex与y=ln(x-a)的图象在(0,+∞)上有交点,
易知y=-ex在(0,+∞)上单调递减,且当x=0时,y=-1;y=ln(x-a)在(a,+∞)上单调递增.
a的大小影响函数图象的相对位置,故需分情况讨论并求解.
当a≥0时,易知两函数图象在(0,+∞)上必有交点,满足题意;
当a<0时,如图所示,
只需ln(-a)<-1,所以-
7.解析 (1)当m=0时, f(x)=(3x+1)=-2,所以3x+1==9,所以x=log38.
(2)若f(x)是偶函数,则f(-x)=f(x),所以(3-x+1)+mx=(3x+1)-mx,即 2mx=(3x+1)-(3-x+1)==-x,所以m=-.
(3)当m=-时, f(x)=(3x+1)+x=(3x+1)+==()x+,
令g(x)=()x+,任取x1,x2∈(0,+∞),且x1
所以g(x1)-g(x2)<0,
即g(x)=()x+在(0,+∞)上单调递增,
由复合函数的单调性可知f(x)在(0,+∞)上单调递减,
又由(2)知,当m=-时, f(x)是偶函数,
所以f(x)在(-∞,0)上单调递增,
则f(x)≤f(0)=-log32,
讨论b与-log32的大小关系,进而确定方程f(x)=b的根的个数.
当b>-log32时,方程f(x)=b没有实数根;
当b=-log32时,方程f(x)=b有且仅有1个实数根;
当 b<-log32时,取-2b∈(0,+∞),则f(-2b)==(3-b+3b)<3-b=b,
所以当x∈(0,-2b)时, f(0)=-log32>b, f(-2b)
所以b<-log32时,方程f(x)=b有2个实数根.
综上所述,当b>-log32时,方程没有实数根;
当b=-log32时,方程有且仅有1个实数根;
当 b<-log32时,方程有2个实数根.
思想方法 在本章中,分类讨论思想主要用于解决函数零点及分段函数问题,主要体现在以下几个方面:(1)根据零点在不同的区间分情况讨论,求出零点;(2)根据函数在不同区间的取值讨论函数的解析式及对应性质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
