山东省聊城颐中外国语学校2023-2024学年高一下学期第三次质量检测数学试题(含答案)
文档属性
| 名称 | 山东省聊城颐中外国语学校2023-2024学年高一下学期第三次质量检测数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 395.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-20 20:41:05 | ||
图片预览



文档简介
2023-2024学年第二学期第三次教学质量检测
数学试题
单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设z1=3-4i,z2=-2+3i,则z1-z2在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.三棱锥的底面为直角边长分别是2和3的直角三角形,高为4,则该三棱锥的体积为( )
A.4 B.6 C.12 D.24
3.已知|a|=2,|b|=1,a与b之间的夹角为60°,那么向量a-4b的模为( )
A.2 B.2 C.6 D.12
4.如果直线a∥平面α,那么直线a与平面α内的( )
A.一条直线不相交 B.两条直线不相交
C.无数条直线不相交 D.任意一条直线不相交
5.如图,在三棱锥D-ABC中,AC=BD,且AC⊥BD,E,F分别是棱DC,AB的中点,则EF和AC所成的角等于( )
A.30° B.45° C.60° D.90°
6.已知一组数据从小到大排列为-1,0,4,x,6,15,且这组数据的中位数是5,那么这组数据的众数为( )
A.5 B.6 C.4 D.5.5
7.数据12,14,15,17,19,23,27,30的第70百分位数是( )
A.14 B.17 C.19 D.23
8.从某项综合能力测试中抽取了100人的成绩,统计如下表所示,则这100人成绩的标准差为( )
分数 5 4 3 2 1
人数 20 10 30 30 10
A. B. C.3 D.
多项选择题(本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.在某次高中学科竞赛中,4 000名考生的参赛成绩统计如图所示,60分以下视为不及格,若同一组中数据用该组区间的中点值作代表,则下列说法中正确的是( )
A.成绩在[70,80)内的考生人数最多
B.不及格的考生人数为1 000
C.考生竞赛成绩的平均分约为70.5分
D.考生竞赛成绩的中位数为75分
10.已知平面α⊥平面β,α∩β=l,点A∈α,A l,若直线AB∥l,直线AC⊥l,直线m∥α,m∥β,则( )
A.AB∥m B.AC⊥m C.AB∥β D.AC⊥β
11.已知三棱锥S-ABC的所有顶点都在球O的球面上,△ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则( )
A.三棱锥S-ABC的体积为
B.三棱锥S-ABC的体积为
C.三棱锥O-ABC的体积为
D.三棱锥O-ABC的体积为
填空题(本题共3小题,每小题5分,共15分)
12.计算:=________.
13.某学校高一、高二、高三年级的学生人数之比为3∶3∶4,现用分层随机抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则应从高二年级抽取________名学生.
14.已知数据x1,x2,…,xn的平均数为=5,则数据2x1+1,2x2+1,…,2xn+1的平均数为________.
解答题(本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)
15.(13分)已知向量a,b反向,b=(-1,-2),a·b=-20.
(1)求向量a的坐标.
(2)若c=(2,1),求(b·c)a.
16(15分).设△ABC的内角A,B,C所对边的长分别为a,b,c,且有2sin Bcos A=sin Acos C+cos Asin C.
(1)求角A的大小;
(2)若b=2,c=1,D为BC的中点,求AD的长.
17.(15分)某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成,,,,,六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
(1)求分数内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试成绩的众数和中位数和平均数.
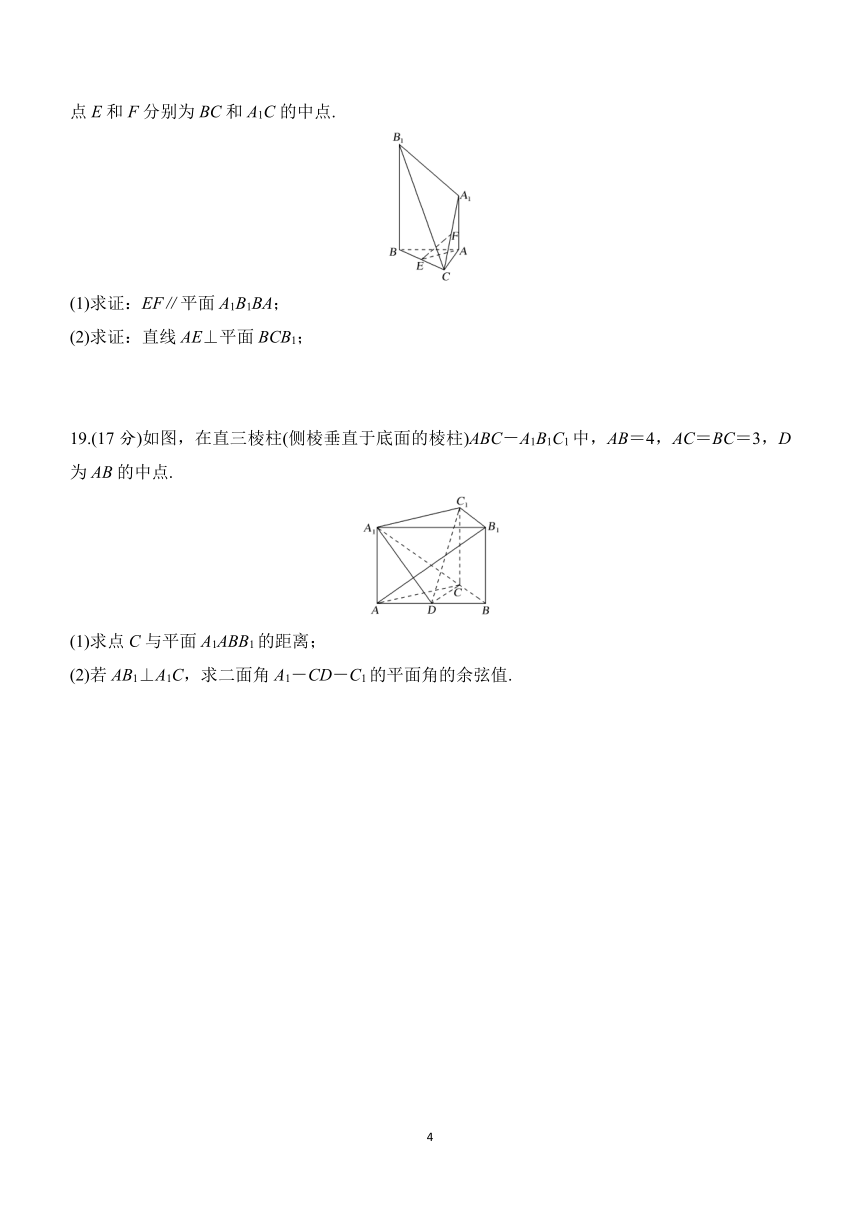
18.(17分)如图,已知AA1⊥平面ABC,BB1∥AA1,AB=AC=3,BC=2,AA1=,BB1=2,点E和F分别为BC和A1C的中点.
(1)求证:EF∥平面A1B1BA;
(2)求证:直线AE⊥平面BCB1;
19.(17分)如图,在直三棱柱(侧棱垂直于底面的棱柱)ABC-A1B1C1中,AB=4,AC=BC=3,D为AB的中点.
(1)求点C与平面A1ABB1的距离;
(2)若AB1⊥A1C,求二面角A1-CD-C1的平面角的余弦值.
数学试题答案
1.解析 ∵z1-z2=(3-4i)-(-2+3i)=5-7i,
∴z1-z2在复平面内对应的点位于第四象限.答案 D
2.解析 V=Sh=××2×3×4=4.答案 A
3.解析 ∵|a-4b|2=a2-8a·b+16b2=22-8×2×1×cos 60°+16×12=12,∴|a-4b|=2.答案 B
4.解析 直线a∥平面α,则a与α无公共点,与α内的直线当然均无公共点.
答案 D
5.解析 如图所示,取BC的中点G,连接FG,EG.
∵E,F分别是CD,AB的中点,∴FG∥AC,EG∥BD,
且FG=AC,EG=BD.∴∠EFG为EF与AC所成的角(或其补角).
又∵AC=BD,∴FG=EG.又∵AC⊥BD,∴FG⊥EG,∴∠FGE=90°,
∴△EFG为等腰直角三角形,∴∠EFG=45°,即EF与AC所成的角为45°.
答案 B
6.解析 由题意得(4+x)=5,得x=6,从而这组数据的众数为6.答案 B
7.解析 因为8×70%=5.6,故70%分位数是第六项数据23.答案 D
8.解析 ∵==3,
∴s2=(20×22+10×12+30×12+10×22)==,∴s=.
9.解析 由频率分布直方图可得,成绩在[70,80)内的频率最高,因此考生人数最多,故A正确;由频率分布直方图可得,成绩在[40,60)内的频率为10×(0.01+0.015)=0.25,因此不及格的人数为4 000×0.25=1 000,故B正确;C选项,由频率分布直方图可得,平均分约为45×0.1+55×0.15+65×0.2+75×0.3+85×0.15+95×0.1=70.5(分),故C正确;因为成绩在[40,70)内的频率为10×(0.01+0.015+0.02)=0.45,在[70,80)内的频率为0.3,所以中位数为70+10×≈71.67,故D错误.故选ABC.答案 ABC
10.解析 因为m∥α,m∥β,α∩β=l,∴m∥l,又AB∥l,所以AB∥m,故A正确;
因为AC⊥l,m∥l,所以AC⊥m,故B正确;
因为A∈α,AB∥l,l α,所以B∈α,所以AB β,l β,所以AB∥β,故C正确;
因为AC⊥l,当点C在α内时,AC⊥β成立,当点C不在α内时,AC⊥β不成立,故D不正确.
答案 ABC
11.解析 由于三棱锥S-ABC与三棱锥O-ABC的底面都是△ABC,O是SC的中点,因此三棱锥S-ABC的高是三棱锥O-ABC高的2倍,所以三棱锥S-ABC的体积也是三棱锥O-ABC体积的2倍.在三棱锥O-ABC中,其棱长都为1,如图,S△ABC=,高OD==,则VO-ABC=××=,VS-ABC=2VO-ABC=.
答案 AC
12.解析 ====+i.
答案 +i
13.解析 高二年级学生人数占总数的,样本量为50,则应从高二年级抽取50×=15(名)学生.答案 15
14.解析 所求平均数为2+1=2×5+1=11.答案 11
15.解 (1)因为向量a,b反向,
又b=(-1,-2).
所以设a=λb=λ(-1,-2)=(-λ,-2λ),λ<0.
由a·b=-20得-1×(-λ)+(-2)×(-2λ)=-20,
所以λ=-4,所以a=(4,8).
(2)因为b·c=(-1,-2)·(2,1)=-1×2+(-2)×1=-4,
所以(b·c)a=-4(4,8)=(-16,-32)
16.解 (1)法一 由题设知,
2sin Bcos A=sin(A+C)=sin B,
因为sin B≠0,
所以cos A=.
由于0法二 由题设可知,
2b·=a·+c·,
于是b2+c2-a2=bc,
所以cos A==.
由于0(2)法一 因为2==(2+2+2·)
==,
所以||=,从而AD=.
法二 因为a2=b2+c2-2bccos A=4+1-2×2×1×=3,
所以a2+c2=b2,B=.所以BD=,AB=1,
所以AD==.
17.(1)设分数内的频率为,根据频率分布直方图,则有
,解得.
所以频率分布直方图为
(2)因为在分数内的频率值最大,所以众数为;
以中位数为准做一条垂直于横轴的直线,这条直线将频率分布直方图分为面积相等的两部分,因为,所以中位数在内,
因为分数内的频率为0.3,而,
所以中位数在区间中从左数处,所以中位数为;
平均数为,
故本次考试成绩的众数为75;中位数为;平均数为71.
18(1)证明 如图,连接A1B.
在△A1BC中,因为E和F分别是BC和A1C的中点,所以EF∥BA1.
又因为EF 平面A1B1BA,BA1 平面A1B1BA,
所以EF∥平面A1B1BA.
(2)证明 因为AB=AC,E为BC的中点,
所以AE⊥BC.
因为AA1⊥平面ABC,BB1∥AA1,所以BB1⊥平面ABC,
又AE 平面ABC,从而BB1⊥AE.
又因为BC∩BB1=B,BC,BB1 平面BCB1,
所以AE⊥平面BCB1.
19.解 (1)由AC=BC,D为AB的中点,得CD⊥AB,又CD⊥AA1,AB∩AA1=A,AB,AA1 平面A1ABB1,得CD⊥平面A1ABB1,所以C到平面A1ABB1的距离为CD==.
(2)如图,取D1为A1B1的中点,
连接DD1,
则DD1∥AA1∥CC1.
又由(1)知CD⊥平面A1ABB1,
又A1D,DD1 平面A1ABB1,
故CD⊥A1D,CD⊥DD1,
所以∠A1DD1为所求的二面角A1-CD-C1的平面角.
因CD⊥平面A1ABB1,AB1 平面A1ABB1,
所以AB1⊥CD,
又已知AB1⊥A1C,A1C∩CD=C,A1C,CD 平面A1CD,
所以AB1⊥平面A1CD,故AB1⊥A1D,从而∠A1AB1,∠A1DA都与∠B1AB互余,因此∠A1AB1=∠A1DA,
所以Rt△A1AD∽Rt△B1A1A.
因此=,即AA=AD·A1B1=8,
得A1A=2.从而A1D=eq \r(AA+AD2)=2.
所以,在Rt△A1DD1中,
cos ∠A1DD1===.
数学试题
单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设z1=3-4i,z2=-2+3i,则z1-z2在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.三棱锥的底面为直角边长分别是2和3的直角三角形,高为4,则该三棱锥的体积为( )
A.4 B.6 C.12 D.24
3.已知|a|=2,|b|=1,a与b之间的夹角为60°,那么向量a-4b的模为( )
A.2 B.2 C.6 D.12
4.如果直线a∥平面α,那么直线a与平面α内的( )
A.一条直线不相交 B.两条直线不相交
C.无数条直线不相交 D.任意一条直线不相交
5.如图,在三棱锥D-ABC中,AC=BD,且AC⊥BD,E,F分别是棱DC,AB的中点,则EF和AC所成的角等于( )
A.30° B.45° C.60° D.90°
6.已知一组数据从小到大排列为-1,0,4,x,6,15,且这组数据的中位数是5,那么这组数据的众数为( )
A.5 B.6 C.4 D.5.5
7.数据12,14,15,17,19,23,27,30的第70百分位数是( )
A.14 B.17 C.19 D.23
8.从某项综合能力测试中抽取了100人的成绩,统计如下表所示,则这100人成绩的标准差为( )
分数 5 4 3 2 1
人数 20 10 30 30 10
A. B. C.3 D.
多项选择题(本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.在某次高中学科竞赛中,4 000名考生的参赛成绩统计如图所示,60分以下视为不及格,若同一组中数据用该组区间的中点值作代表,则下列说法中正确的是( )
A.成绩在[70,80)内的考生人数最多
B.不及格的考生人数为1 000
C.考生竞赛成绩的平均分约为70.5分
D.考生竞赛成绩的中位数为75分
10.已知平面α⊥平面β,α∩β=l,点A∈α,A l,若直线AB∥l,直线AC⊥l,直线m∥α,m∥β,则( )
A.AB∥m B.AC⊥m C.AB∥β D.AC⊥β
11.已知三棱锥S-ABC的所有顶点都在球O的球面上,△ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则( )
A.三棱锥S-ABC的体积为
B.三棱锥S-ABC的体积为
C.三棱锥O-ABC的体积为
D.三棱锥O-ABC的体积为
填空题(本题共3小题,每小题5分,共15分)
12.计算:=________.
13.某学校高一、高二、高三年级的学生人数之比为3∶3∶4,现用分层随机抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则应从高二年级抽取________名学生.
14.已知数据x1,x2,…,xn的平均数为=5,则数据2x1+1,2x2+1,…,2xn+1的平均数为________.
解答题(本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)
15.(13分)已知向量a,b反向,b=(-1,-2),a·b=-20.
(1)求向量a的坐标.
(2)若c=(2,1),求(b·c)a.
16(15分).设△ABC的内角A,B,C所对边的长分别为a,b,c,且有2sin Bcos A=sin Acos C+cos Asin C.
(1)求角A的大小;
(2)若b=2,c=1,D为BC的中点,求AD的长.
17.(15分)某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成,,,,,六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
(1)求分数内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试成绩的众数和中位数和平均数.
18.(17分)如图,已知AA1⊥平面ABC,BB1∥AA1,AB=AC=3,BC=2,AA1=,BB1=2,点E和F分别为BC和A1C的中点.
(1)求证:EF∥平面A1B1BA;
(2)求证:直线AE⊥平面BCB1;
19.(17分)如图,在直三棱柱(侧棱垂直于底面的棱柱)ABC-A1B1C1中,AB=4,AC=BC=3,D为AB的中点.
(1)求点C与平面A1ABB1的距离;
(2)若AB1⊥A1C,求二面角A1-CD-C1的平面角的余弦值.
数学试题答案
1.解析 ∵z1-z2=(3-4i)-(-2+3i)=5-7i,
∴z1-z2在复平面内对应的点位于第四象限.答案 D
2.解析 V=Sh=××2×3×4=4.答案 A
3.解析 ∵|a-4b|2=a2-8a·b+16b2=22-8×2×1×cos 60°+16×12=12,∴|a-4b|=2.答案 B
4.解析 直线a∥平面α,则a与α无公共点,与α内的直线当然均无公共点.
答案 D
5.解析 如图所示,取BC的中点G,连接FG,EG.
∵E,F分别是CD,AB的中点,∴FG∥AC,EG∥BD,
且FG=AC,EG=BD.∴∠EFG为EF与AC所成的角(或其补角).
又∵AC=BD,∴FG=EG.又∵AC⊥BD,∴FG⊥EG,∴∠FGE=90°,
∴△EFG为等腰直角三角形,∴∠EFG=45°,即EF与AC所成的角为45°.
答案 B
6.解析 由题意得(4+x)=5,得x=6,从而这组数据的众数为6.答案 B
7.解析 因为8×70%=5.6,故70%分位数是第六项数据23.答案 D
8.解析 ∵==3,
∴s2=(20×22+10×12+30×12+10×22)==,∴s=.
9.解析 由频率分布直方图可得,成绩在[70,80)内的频率最高,因此考生人数最多,故A正确;由频率分布直方图可得,成绩在[40,60)内的频率为10×(0.01+0.015)=0.25,因此不及格的人数为4 000×0.25=1 000,故B正确;C选项,由频率分布直方图可得,平均分约为45×0.1+55×0.15+65×0.2+75×0.3+85×0.15+95×0.1=70.5(分),故C正确;因为成绩在[40,70)内的频率为10×(0.01+0.015+0.02)=0.45,在[70,80)内的频率为0.3,所以中位数为70+10×≈71.67,故D错误.故选ABC.答案 ABC
10.解析 因为m∥α,m∥β,α∩β=l,∴m∥l,又AB∥l,所以AB∥m,故A正确;
因为AC⊥l,m∥l,所以AC⊥m,故B正确;
因为A∈α,AB∥l,l α,所以B∈α,所以AB β,l β,所以AB∥β,故C正确;
因为AC⊥l,当点C在α内时,AC⊥β成立,当点C不在α内时,AC⊥β不成立,故D不正确.
答案 ABC
11.解析 由于三棱锥S-ABC与三棱锥O-ABC的底面都是△ABC,O是SC的中点,因此三棱锥S-ABC的高是三棱锥O-ABC高的2倍,所以三棱锥S-ABC的体积也是三棱锥O-ABC体积的2倍.在三棱锥O-ABC中,其棱长都为1,如图,S△ABC=,高OD==,则VO-ABC=××=,VS-ABC=2VO-ABC=.
答案 AC
12.解析 ====+i.
答案 +i
13.解析 高二年级学生人数占总数的,样本量为50,则应从高二年级抽取50×=15(名)学生.答案 15
14.解析 所求平均数为2+1=2×5+1=11.答案 11
15.解 (1)因为向量a,b反向,
又b=(-1,-2).
所以设a=λb=λ(-1,-2)=(-λ,-2λ),λ<0.
由a·b=-20得-1×(-λ)+(-2)×(-2λ)=-20,
所以λ=-4,所以a=(4,8).
(2)因为b·c=(-1,-2)·(2,1)=-1×2+(-2)×1=-4,
所以(b·c)a=-4(4,8)=(-16,-32)
16.解 (1)法一 由题设知,
2sin Bcos A=sin(A+C)=sin B,
因为sin B≠0,
所以cos A=.
由于0
2b·=a·+c·,
于是b2+c2-a2=bc,
所以cos A==.
由于0
==,
所以||=,从而AD=.
法二 因为a2=b2+c2-2bccos A=4+1-2×2×1×=3,
所以a2+c2=b2,B=.所以BD=,AB=1,
所以AD==.
17.(1)设分数内的频率为,根据频率分布直方图,则有
,解得.
所以频率分布直方图为
(2)因为在分数内的频率值最大,所以众数为;
以中位数为准做一条垂直于横轴的直线,这条直线将频率分布直方图分为面积相等的两部分,因为,所以中位数在内,
因为分数内的频率为0.3,而,
所以中位数在区间中从左数处,所以中位数为;
平均数为,
故本次考试成绩的众数为75;中位数为;平均数为71.
18(1)证明 如图,连接A1B.
在△A1BC中,因为E和F分别是BC和A1C的中点,所以EF∥BA1.
又因为EF 平面A1B1BA,BA1 平面A1B1BA,
所以EF∥平面A1B1BA.
(2)证明 因为AB=AC,E为BC的中点,
所以AE⊥BC.
因为AA1⊥平面ABC,BB1∥AA1,所以BB1⊥平面ABC,
又AE 平面ABC,从而BB1⊥AE.
又因为BC∩BB1=B,BC,BB1 平面BCB1,
所以AE⊥平面BCB1.
19.解 (1)由AC=BC,D为AB的中点,得CD⊥AB,又CD⊥AA1,AB∩AA1=A,AB,AA1 平面A1ABB1,得CD⊥平面A1ABB1,所以C到平面A1ABB1的距离为CD==.
(2)如图,取D1为A1B1的中点,
连接DD1,
则DD1∥AA1∥CC1.
又由(1)知CD⊥平面A1ABB1,
又A1D,DD1 平面A1ABB1,
故CD⊥A1D,CD⊥DD1,
所以∠A1DD1为所求的二面角A1-CD-C1的平面角.
因CD⊥平面A1ABB1,AB1 平面A1ABB1,
所以AB1⊥CD,
又已知AB1⊥A1C,A1C∩CD=C,A1C,CD 平面A1CD,
所以AB1⊥平面A1CD,故AB1⊥A1D,从而∠A1AB1,∠A1DA都与∠B1AB互余,因此∠A1AB1=∠A1DA,
所以Rt△A1AD∽Rt△B1A1A.
因此=,即AA=AD·A1B1=8,
得A1A=2.从而A1D=eq \r(AA+AD2)=2.
所以,在Rt△A1DD1中,
cos ∠A1DD1===.
同课章节目录
