【沪科版八上同步练习】 第13章三角形边角关系和命题证明综合测试题
文档属性
| 名称 | 【沪科版八上同步练习】 第13章三角形边角关系和命题证明综合测试题 |  | |
| 格式 | doc | ||
| 文件大小 | 15.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-20 23:15:53 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【沪科版八上同步练习】
第13章三角形边角关系和命题证明综合测试题
一、单选题
1.若一个三角形的两边长分别为3和7,则第三边长可能是( )
A.6 B.3 C.2 D.11
2.下列线段能构成三角形的是( )
A.3,3,5 B.2,2,5 C.1,2,3 D.2,3,6
3.下列长度的各组线段,能组成三角形的是( )
A. , , B. , ,
C. , , D. , ,
4.下列各组数分别是三根小木棒的长度,将它们首尾相连能摆成三角形的是( )
A.3cm,4cm,8cm B.4cm,4cm,8cm
C.5cm,6cm,8cm D.5cm,5cm,12cm
5.如图,在△ABC中,BD为△ABC的角平分线,CE为△ABC的高,CE、BD交于点F,∠A=50°,∠BCA=60°,那么∠BFC的度数是( )
A.115° B.120° C.125° D.130°
二、填空题
6.“全等三角形的面积相等”的逆命题是 .
7.如图,AD是△ABC的一条中线,若BD=3,则BC= .
8.一个三角形的三边分别是x,3,5,那么这个三角形的周长的取值范围是 .
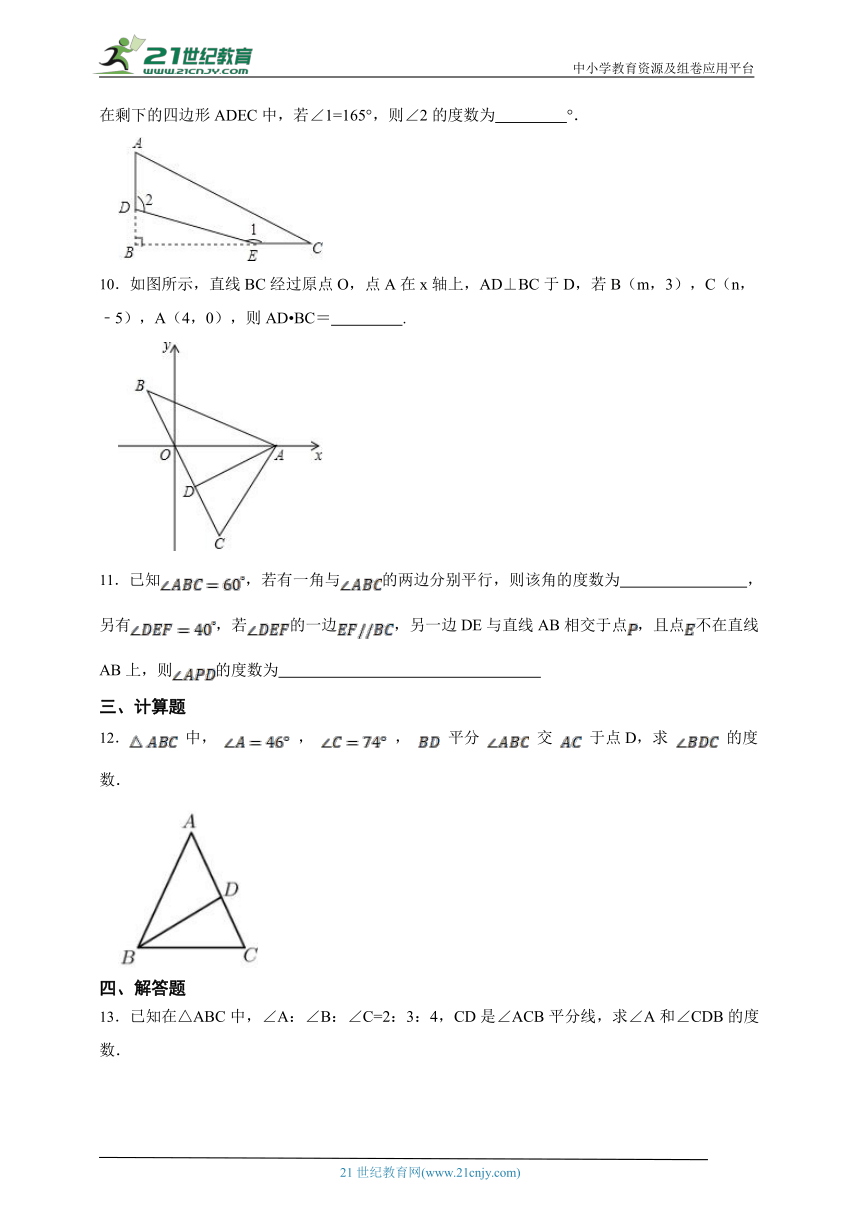
9.有一张直角三角形纸片,记作△ABC,其中∠B=90°.按如图方式剪去它的一个角(虚线部分),在剩下的四边形ADEC中,若∠1=165°,则∠2的度数为 °.
10.如图所示,直线BC经过原点O,点A在x轴上,AD⊥BC于D,若B(m,3),C(n,﹣5),A(4,0),则AD BC= .
11.已知,若有一角与的两边分别平行,则该角的度数为 ,另有,若的一边,另一边DE与直线AB相交于点,且点不在直线AB上,则的度数为
三、计算题
12. 中, , , 平分 交 于点D,求 的度数.
四、解答题
13.已知在△ABC中,∠A:∠B:∠C=2:3:4,CD是∠ACB平分线,求∠A和∠CDB的度数.
14.证明三角形的内角和定理:
已知△ABC(如图),求证:∠A+∠B+∠C=180°.
15. 如图,在三角形中,D,E是上的点,F是上一点,H,G是上的点,于点D,连接,,.给定三个条件:①,②,③.
(1)请在上述三个条件中选择其中两个作为已知条件.另一个作为结论组成一个真命题,你选择的条件是 .结论是 (填写序号);
(2)证明上述命题.
五、综合题
16.已知,如图一: 中, 平分 ,CO平分外角 .
(1)①若 ,则 的度数为 .
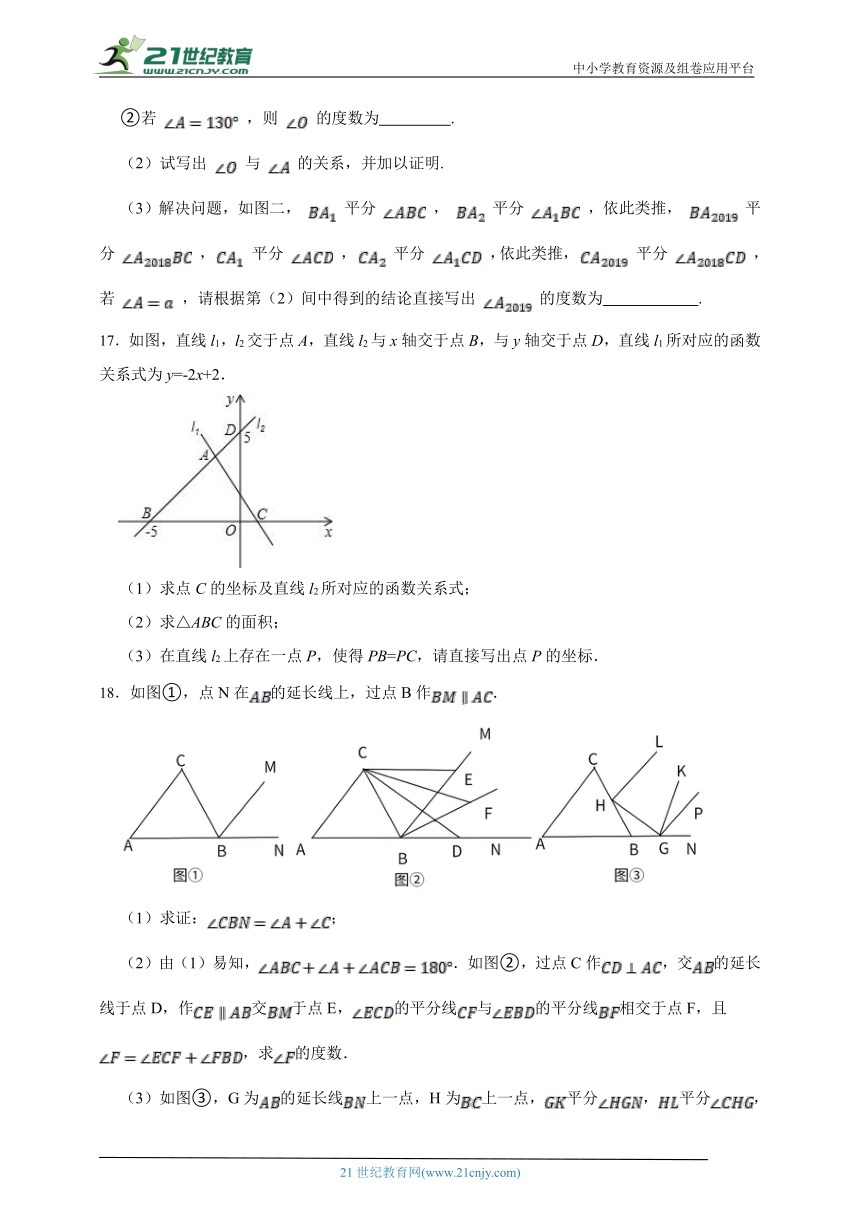
②若 ,则 的度数为 .
(2)试写出 与 的关系,并加以证明.
(3)解决问题,如图二, 平分 , 平分 ,依此类推, 平分 , 平分 , 平分 ,依此类推, 平分 ,若 ,请根据第(2)间中得到的结论直接写出 的度数为 .
17.如图,直线l1,l2交于点A,直线l2与x轴交于点B,与y轴交于点D,直线l1所对应的函数关系式为y=-2x+2.
(1)求点C的坐标及直线l2所对应的函数关系式;
(2)求△ABC的面积;
(3)在直线l2上存在一点P,使得PB=PC,请直接写出点P的坐标.
18.如图①,点N在的延长线上,过点B作.
(1)求证:;
(2)由(1)易知,.如图②,过点C作,交的延长线于点D,作交于点E,的平分线与的平分线相交于点F,且,求的度数.
(3)如图③,G为的延长线上一点,H为上一点,平分,平分,,试猜想与的关系,并说明理由.
六、实践探究题
19.阅读材料:若,求m、n的值.
解:,
,,,.
根据你的观察,探究下面的问题:
(1)已知,求的值;
(2)已知等腰△ABC的三边长a、b、c都是正整数,且满足,求△ABC的周长;
(3)已知,,求的值.
答案解析部分
1.【答案】A
【知识点】三角形三边关系
2.【答案】A
【知识点】三角形三边关系
3.【答案】B
【知识点】三角形三边关系
4.【答案】C
【知识点】三角形三边关系
5.【答案】C
【知识点】三角形的角平分线、中线和高;三角形内角和定理
6.【答案】面积相等的三角形是全等三角形
【知识点】逆命题
7.【答案】6
【知识点】三角形的角平分线、中线和高
8.【答案】10<c<16
【知识点】三角形三边关系
9.【答案】105
【知识点】三角形内角和定理
10.【答案】32
【知识点】三角形的面积
11.【答案】60°或120°;20 °;100 °;80 °;160 °
【知识点】平行线的性质;三角形内角和定理;三角形的外角性质;对顶角及其性质
12.【答案】解:根据三角形内角和是 得
平分 ,
【知识点】三角形内角和定理;角平分线的概念
13.【答案】解:∵在△ABC中,∠A:∠B:∠C=2:3:4,∠A+∠ACB+∠B=180°, ∴ ∠A= ×180°=40°,∠ACB= ×180°=80°, ∵ CD是∠ACB平分线, ∴∠ACD= ∠ACB=40°, ∴∠CDB=∠A+∠ACD=40°+40°=80°
【知识点】三角形的角平分线、中线和高;三角形内角和定理
14.【答案】证明:过点A作EF∥BC,
∵EF∥BC,
∴∠1=∠B,∠2=∠C,
∵∠1+∠2+∠BAC=180°,
∴∠BAC+∠B+∠C=180°.
即三角形内角和等于180°.
【知识点】三角形内角和定理
15.【答案】(1)①②;③
(2)解:若选择的条件是①②,结论是③,
证明:∵,,
∴,
∴,
∵,
∴,则,
∴,
过点作,则,
∴,,
∵,
∴;
若选择的条件是①③,结论是②,
证明:∵,,
∴,
∴,
过点作,则,
∵,,
∴,
∴,
∴,
∴,
则,
∴;
若选择的条件是②③,结论是①,
证明:过点作,则,
∵,,
∴,
∴,
∴,
∴,则,
∵,
∴,
∴,
∵,
∴.
【知识点】平行线的判定与性质;真命题与假命题
16.【答案】(1)35°;65°
(2)解:结论:∠O=
理由:∵BO平分 ,CO平分
∴ ,
设∠OBC=x,∠OCD=y,则∠ABC=2x,∠ACD=2y
∴
∵
∴
∴
(3)
【知识点】三角形的外角性质
17.【答案】(1)解:由y=-2x+2,令y=0,得-2x+2=0.
∴x=1.
∴C(1,0).
设直线l2所对应的函数关系式为y=kx+b,
由图象知:直线l2经过点B(-5,0),D(0,5)
∴ ,
解得 .
∴直线l2所对应的函数关系式为y=x+5.
(2)解:由 ,
解得
∴A(-1,4).
∵BC=6,
∴S△ABC= ×6×4=12.
(3)P(-2,3)
【知识点】两一次函数图象相交或平行问题;三角形的面积;一次函数图象与坐标轴交点问题
18.【答案】(1)证明:∵,
∴,
∵,
∴;
(2)解:∵,
∴,
∵,
∴,
∵,
∴,
∵的平分线与的平分线相交于点F,
∴,,
∴
;
(3)解:.理由见解析.
∵平分,平分,
∴,,
∵,
∴,
∴,
∴,
∵
,
∵,
∴,
∴.
【知识点】平行线的性质;三角形内角和定理;角平分线的概念
19.【答案】(1)解:,
,
,
,,解得:,;则;
(2)解:,
,
,则,,解得:,,
由三角形三边关系可知,三角形三边分别为1、3、3,
的周长为1+3+3=7;
(3)解:,,则,
,
,则,,解得,,,.
【知识点】完全平方公式及运用;因式分解﹣公式法;三角形三边关系;偶次方的非负性
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【沪科版八上同步练习】
第13章三角形边角关系和命题证明综合测试题
一、单选题
1.若一个三角形的两边长分别为3和7,则第三边长可能是( )
A.6 B.3 C.2 D.11
2.下列线段能构成三角形的是( )
A.3,3,5 B.2,2,5 C.1,2,3 D.2,3,6
3.下列长度的各组线段,能组成三角形的是( )
A. , , B. , ,
C. , , D. , ,
4.下列各组数分别是三根小木棒的长度,将它们首尾相连能摆成三角形的是( )
A.3cm,4cm,8cm B.4cm,4cm,8cm
C.5cm,6cm,8cm D.5cm,5cm,12cm
5.如图,在△ABC中,BD为△ABC的角平分线,CE为△ABC的高,CE、BD交于点F,∠A=50°,∠BCA=60°,那么∠BFC的度数是( )
A.115° B.120° C.125° D.130°
二、填空题
6.“全等三角形的面积相等”的逆命题是 .
7.如图,AD是△ABC的一条中线,若BD=3,则BC= .
8.一个三角形的三边分别是x,3,5,那么这个三角形的周长的取值范围是 .
9.有一张直角三角形纸片,记作△ABC,其中∠B=90°.按如图方式剪去它的一个角(虚线部分),在剩下的四边形ADEC中,若∠1=165°,则∠2的度数为 °.
10.如图所示,直线BC经过原点O,点A在x轴上,AD⊥BC于D,若B(m,3),C(n,﹣5),A(4,0),则AD BC= .
11.已知,若有一角与的两边分别平行,则该角的度数为 ,另有,若的一边,另一边DE与直线AB相交于点,且点不在直线AB上,则的度数为
三、计算题
12. 中, , , 平分 交 于点D,求 的度数.
四、解答题
13.已知在△ABC中,∠A:∠B:∠C=2:3:4,CD是∠ACB平分线,求∠A和∠CDB的度数.
14.证明三角形的内角和定理:
已知△ABC(如图),求证:∠A+∠B+∠C=180°.
15. 如图,在三角形中,D,E是上的点,F是上一点,H,G是上的点,于点D,连接,,.给定三个条件:①,②,③.
(1)请在上述三个条件中选择其中两个作为已知条件.另一个作为结论组成一个真命题,你选择的条件是 .结论是 (填写序号);
(2)证明上述命题.
五、综合题
16.已知,如图一: 中, 平分 ,CO平分外角 .
(1)①若 ,则 的度数为 .
②若 ,则 的度数为 .
(2)试写出 与 的关系,并加以证明.
(3)解决问题,如图二, 平分 , 平分 ,依此类推, 平分 , 平分 , 平分 ,依此类推, 平分 ,若 ,请根据第(2)间中得到的结论直接写出 的度数为 .
17.如图,直线l1,l2交于点A,直线l2与x轴交于点B,与y轴交于点D,直线l1所对应的函数关系式为y=-2x+2.
(1)求点C的坐标及直线l2所对应的函数关系式;
(2)求△ABC的面积;
(3)在直线l2上存在一点P,使得PB=PC,请直接写出点P的坐标.
18.如图①,点N在的延长线上,过点B作.
(1)求证:;
(2)由(1)易知,.如图②,过点C作,交的延长线于点D,作交于点E,的平分线与的平分线相交于点F,且,求的度数.
(3)如图③,G为的延长线上一点,H为上一点,平分,平分,,试猜想与的关系,并说明理由.
六、实践探究题
19.阅读材料:若,求m、n的值.
解:,
,,,.
根据你的观察,探究下面的问题:
(1)已知,求的值;
(2)已知等腰△ABC的三边长a、b、c都是正整数,且满足,求△ABC的周长;
(3)已知,,求的值.
答案解析部分
1.【答案】A
【知识点】三角形三边关系
2.【答案】A
【知识点】三角形三边关系
3.【答案】B
【知识点】三角形三边关系
4.【答案】C
【知识点】三角形三边关系
5.【答案】C
【知识点】三角形的角平分线、中线和高;三角形内角和定理
6.【答案】面积相等的三角形是全等三角形
【知识点】逆命题
7.【答案】6
【知识点】三角形的角平分线、中线和高
8.【答案】10<c<16
【知识点】三角形三边关系
9.【答案】105
【知识点】三角形内角和定理
10.【答案】32
【知识点】三角形的面积
11.【答案】60°或120°;20 °;100 °;80 °;160 °
【知识点】平行线的性质;三角形内角和定理;三角形的外角性质;对顶角及其性质
12.【答案】解:根据三角形内角和是 得
平分 ,
【知识点】三角形内角和定理;角平分线的概念
13.【答案】解:∵在△ABC中,∠A:∠B:∠C=2:3:4,∠A+∠ACB+∠B=180°, ∴ ∠A= ×180°=40°,∠ACB= ×180°=80°, ∵ CD是∠ACB平分线, ∴∠ACD= ∠ACB=40°, ∴∠CDB=∠A+∠ACD=40°+40°=80°
【知识点】三角形的角平分线、中线和高;三角形内角和定理
14.【答案】证明:过点A作EF∥BC,
∵EF∥BC,
∴∠1=∠B,∠2=∠C,
∵∠1+∠2+∠BAC=180°,
∴∠BAC+∠B+∠C=180°.
即三角形内角和等于180°.
【知识点】三角形内角和定理
15.【答案】(1)①②;③
(2)解:若选择的条件是①②,结论是③,
证明:∵,,
∴,
∴,
∵,
∴,则,
∴,
过点作,则,
∴,,
∵,
∴;
若选择的条件是①③,结论是②,
证明:∵,,
∴,
∴,
过点作,则,
∵,,
∴,
∴,
∴,
∴,
则,
∴;
若选择的条件是②③,结论是①,
证明:过点作,则,
∵,,
∴,
∴,
∴,
∴,则,
∵,
∴,
∴,
∵,
∴.
【知识点】平行线的判定与性质;真命题与假命题
16.【答案】(1)35°;65°
(2)解:结论:∠O=
理由:∵BO平分 ,CO平分
∴ ,
设∠OBC=x,∠OCD=y,则∠ABC=2x,∠ACD=2y
∴
∵
∴
∴
(3)
【知识点】三角形的外角性质
17.【答案】(1)解:由y=-2x+2,令y=0,得-2x+2=0.
∴x=1.
∴C(1,0).
设直线l2所对应的函数关系式为y=kx+b,
由图象知:直线l2经过点B(-5,0),D(0,5)
∴ ,
解得 .
∴直线l2所对应的函数关系式为y=x+5.
(2)解:由 ,
解得
∴A(-1,4).
∵BC=6,
∴S△ABC= ×6×4=12.
(3)P(-2,3)
【知识点】两一次函数图象相交或平行问题;三角形的面积;一次函数图象与坐标轴交点问题
18.【答案】(1)证明:∵,
∴,
∵,
∴;
(2)解:∵,
∴,
∵,
∴,
∵,
∴,
∵的平分线与的平分线相交于点F,
∴,,
∴
;
(3)解:.理由见解析.
∵平分,平分,
∴,,
∵,
∴,
∴,
∴,
∵
,
∵,
∴,
∴.
【知识点】平行线的性质;三角形内角和定理;角平分线的概念
19.【答案】(1)解:,
,
,
,,解得:,;则;
(2)解:,
,
,则,,解得:,,
由三角形三边关系可知,三角形三边分别为1、3、3,
的周长为1+3+3=7;
(3)解:,,则,
,
,则,,解得,,,.
【知识点】完全平方公式及运用;因式分解﹣公式法;三角形三边关系;偶次方的非负性
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
