【沪科版八上同步练习】 第14.章全等三角形综合测试题(含答案)
文档属性
| 名称 | 【沪科版八上同步练习】 第14.章全等三角形综合测试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-20 23:12:24 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【沪科版八上同步练习】
第14.章全等三角形综合测试题
一、单选题
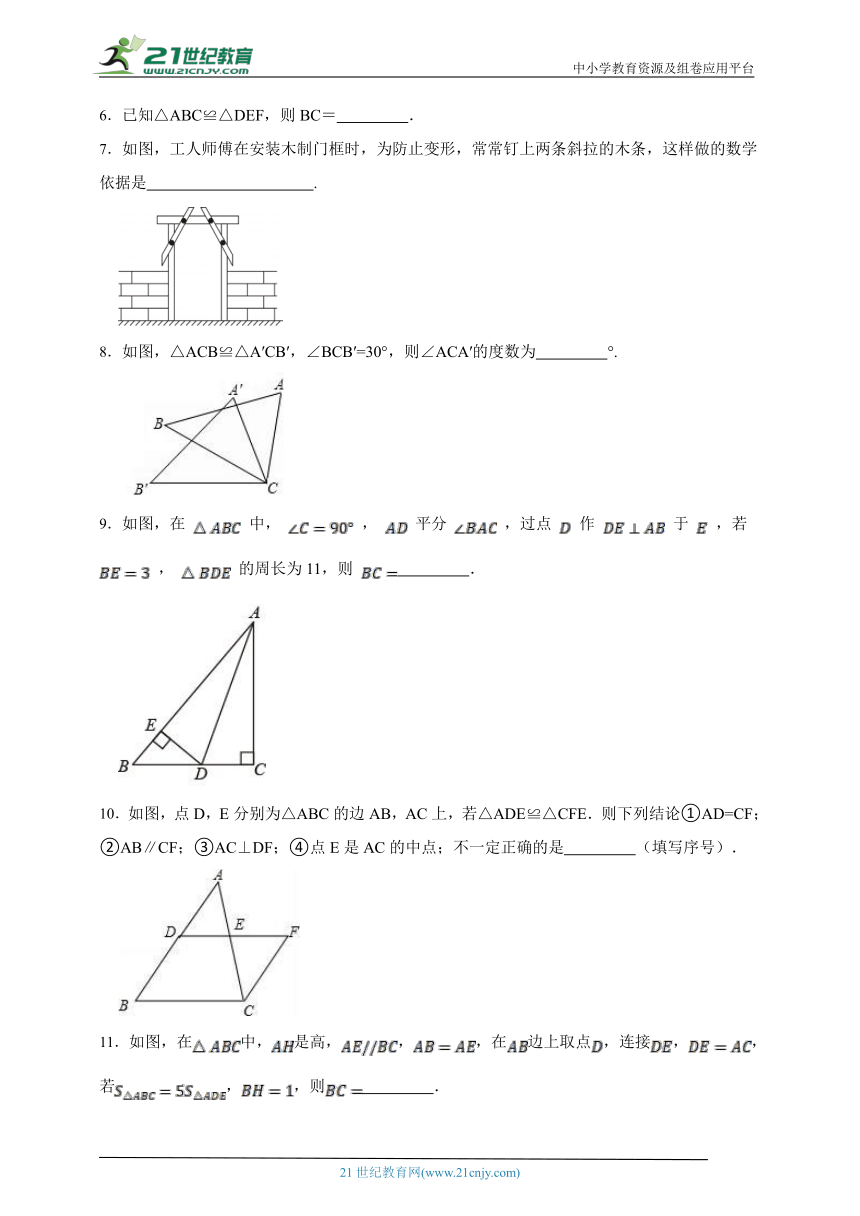
1.如图,某同学把一块三角形的玻璃块打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是( )
A.带①去 B.带②去 C.带③去 D.带①②去
2.下列图形中具有稳定性的是( )
A.五边形 B.六边形 C.等腰三角形 D.平行四边形
3.下列事物所运用的原理不属于三角形稳定性的是( )
A.长方形门框的斜拉条 B.埃及金字塔
C.三角形房架 D.学校的电动伸缩大门
4.如图,若△OAD≌△OBC,且∠O=65°,∠C=20°,则∠OAD=( )
A.20° B.65° C.86° D.95°
5.如图,在中,高和交于点F,添加下列哪个条件( ),不能使得.
A. B. C. D.
二、填空题
6.已知△ABC≌△DEF,则BC= .
7.如图,工人师傅在安装木制门框时,为防止变形,常常钉上两条斜拉的木条,这样做的数学依据是 .
8.如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为 °.
9.如图,在 中, , 平分 ,过点 作 于 ,若 , 的周长为11,则 .
10.如图,点D,E分别为△ABC的边AB,AC上,若△ADE≌△CFE.则下列结论①AD=CF;②AB∥CF;③AC⊥DF;④点E是AC的中点;不一定正确的是 (填写序号).
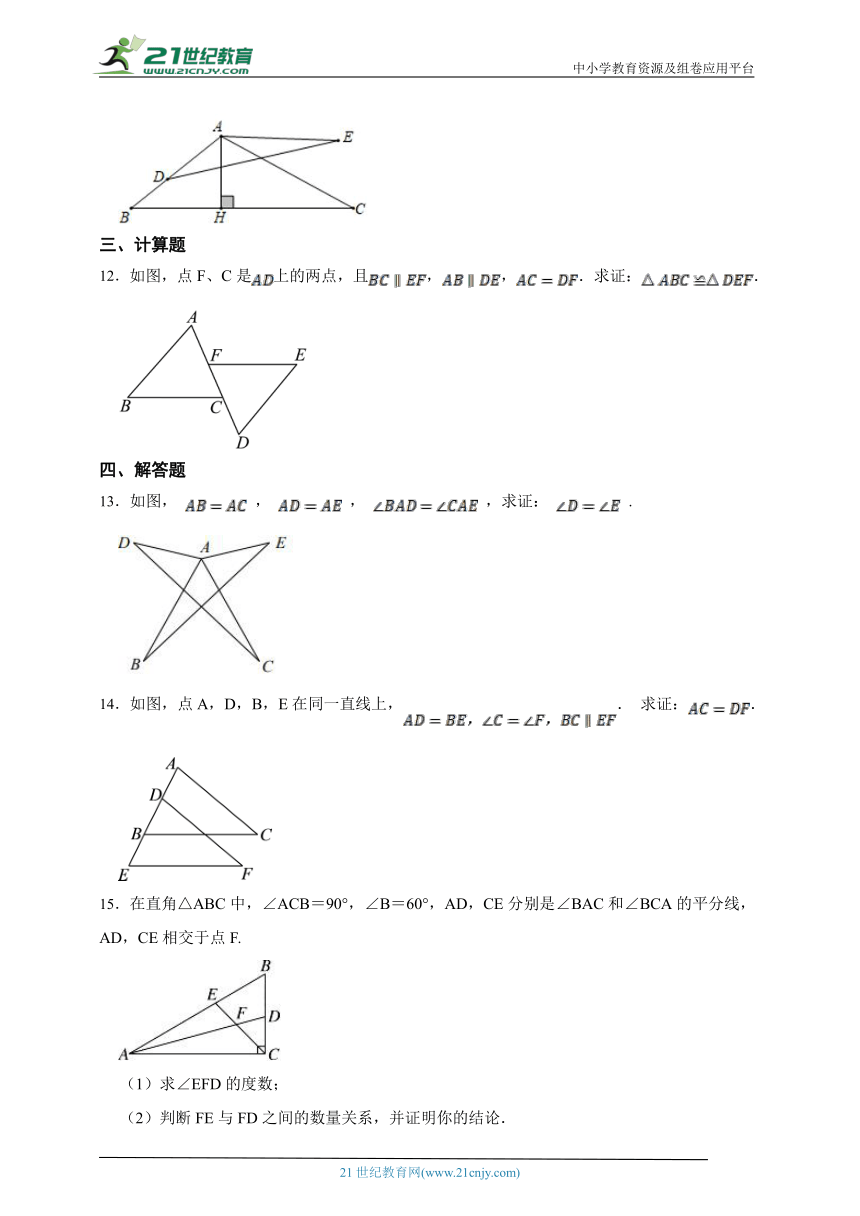
11.如图,在中,是高,,,在边上取点,连接,,若,,则 .
三、计算题
12.如图,点F、C是上的两点,且,,.求证:.
四、解答题
13.如图, , , ,求证: .
14.如图,点A,D,B,E在同一直线上,. 求证:.
15.在直角△ABC中,∠ACB=90°,∠B=60°,AD,CE分别是∠BAC和∠BCA的平分线,AD,CE相交于点F.
(1)求∠EFD的度数;
(2)判断FE与FD之间的数量关系,并证明你的结论.
五、综合题
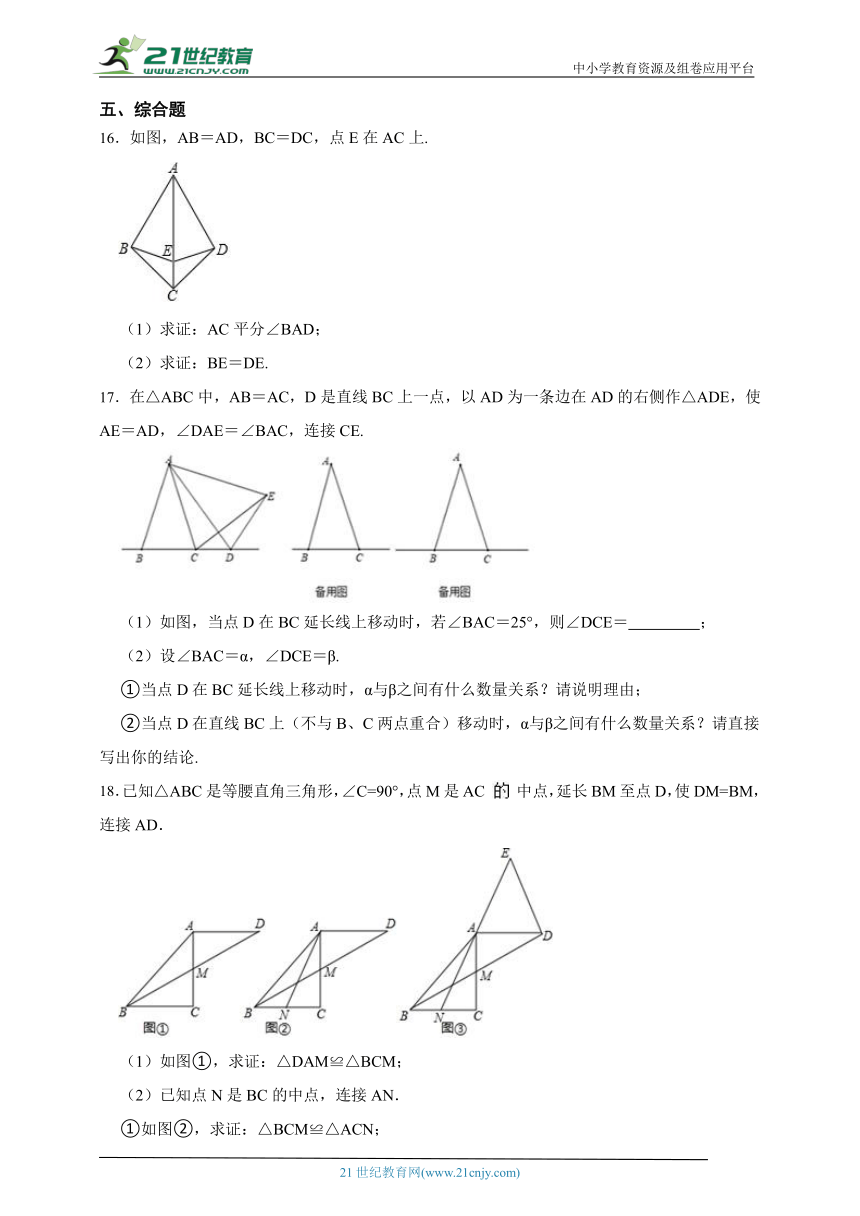
16.如图,AB=AD,BC=DC,点E在AC上.
(1)求证:AC平分∠BAD;
(2)求证:BE=DE.
17.在△ABC中,AB=AC,D是直线BC上一点,以AD为一条边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图,当点D在BC延长线上移动时,若∠BAC=25°,则∠DCE= ;
(2)设∠BAC=α,∠DCE=β.
①当点D在BC延长线上移动时,α与β之间有什么数量关系?请说明理由;
②当点D在直线BC上(不与B、C两点重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.
18.已知△ABC是等腰直角三角形,∠C=90°,点M是AC 中点,延长BM至点D,使DM=BM,连接AD.
(1)如图①,求证:△DAM≌△BCM;
(2)已知点N是BC的中点,连接AN.
①如图②,求证:△BCM≌△ACN;
②如图③,延长NA至点E,使AE=NA,连接DE.求证:BD⊥DE.
六、实践探究题
19.
(1)【探究】如图1,在Rt中,,直线经过点,且点A,B在直线的同侧,过点A,B分别作直线的垂线,垂足分别为点D,E.求证:.
(2)【应用】如图2,在Rt中,,直线经过点,且点A,B在直线的异侧,过点A,B分别作直线的垂线,垂足分别为点D,E.直接写出线段AD,BE,DE之间的数量关系.
答案解析部分
1.【答案】C
【知识点】三角形全等的判定-AAS
2.【答案】C
【知识点】三角形的稳定性
3.【答案】D
【知识点】三角形的稳定性
4.【答案】D
【知识点】三角形全等及其性质
5.【答案】D
【知识点】三角形全等的判定
6.【答案】EF
【知识点】三角形全等及其性质
7.【答案】三角形具有稳定性
【知识点】三角形的稳定性
8.【答案】30
【知识点】三角形全等及其性质
9.【答案】8
【知识点】三角形全等及其性质;三角形全等的判定-AAS
10.【答案】③
【知识点】三角形全等及其性质
11.【答案】
【知识点】三角形的面积;直角三角形全等的判定-HL;三角形全等的判定-AAS
12.【答案】证明:∵,
∴,
∵,
∴,
在和中
,
.
【知识点】三角形全等的判定-ASA
13.【答案】证明:
∵
∴
即
∴在 与 中
∴
∴
【知识点】三角形全等的判定-SAS
14.【答案】证明:∵,
∴,即
∵,
∴
在和中
∵
∴,
∴
【知识点】三角形全等的判定;三角形全等的判定-AAS
15.【答案】(1)解:∵△ABC中,∠ACB=90°,∠B=60°
∴∠BAC=30°,
∵AD、CE分别是∠BAC、∠BCA的平分线
∴∠FAC=∠BAC=15°,∠FCA=∠ACB=45°
∴∠AFC=180°-∠FAC-∠FCA=120°,
∴∠EFD=∠AFC=120°;
(2)解:FE与FD之间的数量关系为FE=FD;
证明:在AC上截取AG=AE,连接FG,
∵AD是∠BAC的平分线,∴∠BAD=∠CAD
又∵AF为公共边
在△EAF和△GAF中
∵AE=AG,∠EAF=∠FAG,AF=AF,
∴△AEF≌△AGF
∴FE=FG,∠AFE=∠AFG=60°,
∴∠CFG=60°,
又∵FC为公共边,∠DCF=∠FCG=45°
在△FDC和△FGC中
∵∠DFC=∠GFC,FC=FC,∠FCG=∠FCD,
∴△CFG≌△CFD,
∴FG=FD
∴FE=FD.
【知识点】三角形的角平分线、中线和高;三角形内角和定理;全等三角形的判定与性质
16.【答案】(1)证明:在△ABC与△ADC中,
∴△ABC≌△ADC(SSS)
∴∠BAC=∠DAC
即AC平分∠BAD
(2)证明:由(1)∠BAE=∠DAE
在△BAE与△DAE中,得
∴△BAE≌△DAE(SAS)
∴BE=DE
【知识点】全等三角形的判定与性质
17.【答案】(1)25°
(2)解:①解:当点D在线段BC的延长线上移动时,α与β之间的数量关系是α=β,
理由是:∵∠DAE=∠BAC,
∴∠DAE+∠CAD=∠BAC+∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中
∵ ,
∴△BAD≌△CAE(SAS),
∴∠B=∠ACE,
∵∠ACD=∠B+∠BAC=∠ACE+∠DCE,
∴∠BAC=∠DCE,
∵∠BAC=α,∠DCE=β,
∴α=β;
【知识点】三角形的外角性质;三角形全等的判定-SAS
18.【答案】(1)解:∵点M是AC的中点,∴AM=CM,
在△DAM和△BCM中,
∵ ,∴△DAM≌△BCM(SAS)
(2)解:①∵点M是AC的中点,点N是BC的中点,∴CM= AC,CN= BC,
∵△ABC是等腰直角三角形,∴AC=BC,∴CM=CN,
在△BCM和△ACN中,∵ ,∴△BCM≌△ACN(SAS);
②取AD中点F,连接EF,
则AD=2AF,
∵△BCM≌△ACN,∴AN=BM,∠CBM=∠CAN,
∵△DAM≌△BCM,∴∠CBM=∠ADM,AD=BC=2CN,
∴AF=CN,∴∠DAC=∠C=90°,∠ADM=∠CBM=∠NAC,
∴AD∥BC,∴∠EAF=∠ANC.
在△EAF和△ANC中,∵ ,∴△EAF≌△ANC(SAS),
∴∠NAC=∠AEF,∠C=∠AFE=90°,∴∠AFE=∠DFE=90°,
∵F为AD的中点,∴AF=DF,
在△AFE和△DFE中, ,
∴△AFE≌△DFE(SAS),
∴∠EAD=∠EDA=∠ANC,
∴∠EDB=∠EDA+∠ADB=∠EAD+∠NAC=180°–∠DAM=180°–90°=90°,
∴BD⊥DE
【知识点】全等三角形的判定与性质
19.【答案】(1)证明:∵AD⊥DE,BE⊥DE,∠ACB=90°,
∴∠ADC=∠ACB=∠BEC=90°,
∴∠DAC+∠DCA=90°,
∠DCA+∠ECB=180°-90°=90°,
∴∠DAC=∠ECB;
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS),
∴AD=CE,DC=BE,
∴DE=DC+CE=BE+AD,
即DE=AD+BE.
(2)解:AD=BE-DE,理由如下:
∵AD⊥CD,BE⊥CE,
∴∠ADC=∠CEB=90°;
又∵∠ACB=90°,
∴∠ACD=∠CBE=90°-∠ECB;
在△ACD与△CBE中,
,
∴△ACD≌△CBE(AAS),
∴CD=BE,AD=CE.
又∵CE=CD-DE,
∴AD=BE-DE.
【知识点】余角、补角及其性质;三角形全等的判定-AAS
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【沪科版八上同步练习】
第14.章全等三角形综合测试题
一、单选题
1.如图,某同学把一块三角形的玻璃块打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是( )
A.带①去 B.带②去 C.带③去 D.带①②去
2.下列图形中具有稳定性的是( )
A.五边形 B.六边形 C.等腰三角形 D.平行四边形
3.下列事物所运用的原理不属于三角形稳定性的是( )
A.长方形门框的斜拉条 B.埃及金字塔
C.三角形房架 D.学校的电动伸缩大门
4.如图,若△OAD≌△OBC,且∠O=65°,∠C=20°,则∠OAD=( )
A.20° B.65° C.86° D.95°
5.如图,在中,高和交于点F,添加下列哪个条件( ),不能使得.
A. B. C. D.
二、填空题
6.已知△ABC≌△DEF,则BC= .
7.如图,工人师傅在安装木制门框时,为防止变形,常常钉上两条斜拉的木条,这样做的数学依据是 .
8.如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为 °.
9.如图,在 中, , 平分 ,过点 作 于 ,若 , 的周长为11,则 .
10.如图,点D,E分别为△ABC的边AB,AC上,若△ADE≌△CFE.则下列结论①AD=CF;②AB∥CF;③AC⊥DF;④点E是AC的中点;不一定正确的是 (填写序号).
11.如图,在中,是高,,,在边上取点,连接,,若,,则 .
三、计算题
12.如图,点F、C是上的两点,且,,.求证:.
四、解答题
13.如图, , , ,求证: .
14.如图,点A,D,B,E在同一直线上,. 求证:.
15.在直角△ABC中,∠ACB=90°,∠B=60°,AD,CE分别是∠BAC和∠BCA的平分线,AD,CE相交于点F.
(1)求∠EFD的度数;
(2)判断FE与FD之间的数量关系,并证明你的结论.
五、综合题
16.如图,AB=AD,BC=DC,点E在AC上.
(1)求证:AC平分∠BAD;
(2)求证:BE=DE.
17.在△ABC中,AB=AC,D是直线BC上一点,以AD为一条边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图,当点D在BC延长线上移动时,若∠BAC=25°,则∠DCE= ;
(2)设∠BAC=α,∠DCE=β.
①当点D在BC延长线上移动时,α与β之间有什么数量关系?请说明理由;
②当点D在直线BC上(不与B、C两点重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.
18.已知△ABC是等腰直角三角形,∠C=90°,点M是AC 中点,延长BM至点D,使DM=BM,连接AD.
(1)如图①,求证:△DAM≌△BCM;
(2)已知点N是BC的中点,连接AN.
①如图②,求证:△BCM≌△ACN;
②如图③,延长NA至点E,使AE=NA,连接DE.求证:BD⊥DE.
六、实践探究题
19.
(1)【探究】如图1,在Rt中,,直线经过点,且点A,B在直线的同侧,过点A,B分别作直线的垂线,垂足分别为点D,E.求证:.
(2)【应用】如图2,在Rt中,,直线经过点,且点A,B在直线的异侧,过点A,B分别作直线的垂线,垂足分别为点D,E.直接写出线段AD,BE,DE之间的数量关系.
答案解析部分
1.【答案】C
【知识点】三角形全等的判定-AAS
2.【答案】C
【知识点】三角形的稳定性
3.【答案】D
【知识点】三角形的稳定性
4.【答案】D
【知识点】三角形全等及其性质
5.【答案】D
【知识点】三角形全等的判定
6.【答案】EF
【知识点】三角形全等及其性质
7.【答案】三角形具有稳定性
【知识点】三角形的稳定性
8.【答案】30
【知识点】三角形全等及其性质
9.【答案】8
【知识点】三角形全等及其性质;三角形全等的判定-AAS
10.【答案】③
【知识点】三角形全等及其性质
11.【答案】
【知识点】三角形的面积;直角三角形全等的判定-HL;三角形全等的判定-AAS
12.【答案】证明:∵,
∴,
∵,
∴,
在和中
,
.
【知识点】三角形全等的判定-ASA
13.【答案】证明:
∵
∴
即
∴在 与 中
∴
∴
【知识点】三角形全等的判定-SAS
14.【答案】证明:∵,
∴,即
∵,
∴
在和中
∵
∴,
∴
【知识点】三角形全等的判定;三角形全等的判定-AAS
15.【答案】(1)解:∵△ABC中,∠ACB=90°,∠B=60°
∴∠BAC=30°,
∵AD、CE分别是∠BAC、∠BCA的平分线
∴∠FAC=∠BAC=15°,∠FCA=∠ACB=45°
∴∠AFC=180°-∠FAC-∠FCA=120°,
∴∠EFD=∠AFC=120°;
(2)解:FE与FD之间的数量关系为FE=FD;
证明:在AC上截取AG=AE,连接FG,
∵AD是∠BAC的平分线,∴∠BAD=∠CAD
又∵AF为公共边
在△EAF和△GAF中
∵AE=AG,∠EAF=∠FAG,AF=AF,
∴△AEF≌△AGF
∴FE=FG,∠AFE=∠AFG=60°,
∴∠CFG=60°,
又∵FC为公共边,∠DCF=∠FCG=45°
在△FDC和△FGC中
∵∠DFC=∠GFC,FC=FC,∠FCG=∠FCD,
∴△CFG≌△CFD,
∴FG=FD
∴FE=FD.
【知识点】三角形的角平分线、中线和高;三角形内角和定理;全等三角形的判定与性质
16.【答案】(1)证明:在△ABC与△ADC中,
∴△ABC≌△ADC(SSS)
∴∠BAC=∠DAC
即AC平分∠BAD
(2)证明:由(1)∠BAE=∠DAE
在△BAE与△DAE中,得
∴△BAE≌△DAE(SAS)
∴BE=DE
【知识点】全等三角形的判定与性质
17.【答案】(1)25°
(2)解:①解:当点D在线段BC的延长线上移动时,α与β之间的数量关系是α=β,
理由是:∵∠DAE=∠BAC,
∴∠DAE+∠CAD=∠BAC+∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中
∵ ,
∴△BAD≌△CAE(SAS),
∴∠B=∠ACE,
∵∠ACD=∠B+∠BAC=∠ACE+∠DCE,
∴∠BAC=∠DCE,
∵∠BAC=α,∠DCE=β,
∴α=β;
【知识点】三角形的外角性质;三角形全等的判定-SAS
18.【答案】(1)解:∵点M是AC的中点,∴AM=CM,
在△DAM和△BCM中,
∵ ,∴△DAM≌△BCM(SAS)
(2)解:①∵点M是AC的中点,点N是BC的中点,∴CM= AC,CN= BC,
∵△ABC是等腰直角三角形,∴AC=BC,∴CM=CN,
在△BCM和△ACN中,∵ ,∴△BCM≌△ACN(SAS);
②取AD中点F,连接EF,
则AD=2AF,
∵△BCM≌△ACN,∴AN=BM,∠CBM=∠CAN,
∵△DAM≌△BCM,∴∠CBM=∠ADM,AD=BC=2CN,
∴AF=CN,∴∠DAC=∠C=90°,∠ADM=∠CBM=∠NAC,
∴AD∥BC,∴∠EAF=∠ANC.
在△EAF和△ANC中,∵ ,∴△EAF≌△ANC(SAS),
∴∠NAC=∠AEF,∠C=∠AFE=90°,∴∠AFE=∠DFE=90°,
∵F为AD的中点,∴AF=DF,
在△AFE和△DFE中, ,
∴△AFE≌△DFE(SAS),
∴∠EAD=∠EDA=∠ANC,
∴∠EDB=∠EDA+∠ADB=∠EAD+∠NAC=180°–∠DAM=180°–90°=90°,
∴BD⊥DE
【知识点】全等三角形的判定与性质
19.【答案】(1)证明:∵AD⊥DE,BE⊥DE,∠ACB=90°,
∴∠ADC=∠ACB=∠BEC=90°,
∴∠DAC+∠DCA=90°,
∠DCA+∠ECB=180°-90°=90°,
∴∠DAC=∠ECB;
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS),
∴AD=CE,DC=BE,
∴DE=DC+CE=BE+AD,
即DE=AD+BE.
(2)解:AD=BE-DE,理由如下:
∵AD⊥CD,BE⊥CE,
∴∠ADC=∠CEB=90°;
又∵∠ACB=90°,
∴∠ACD=∠CBE=90°-∠ECB;
在△ACD与△CBE中,
,
∴△ACD≌△CBE(AAS),
∴CD=BE,AD=CE.
又∵CE=CD-DE,
∴AD=BE-DE.
【知识点】余角、补角及其性质;三角形全等的判定-AAS
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
