第2章 轴对称图形综合素质评价卷(含答案)苏科版数学八年级上册期末复习
文档属性
| 名称 | 第2章 轴对称图形综合素质评价卷(含答案)苏科版数学八年级上册期末复习 |
|
|
| 格式 | docx | ||
| 文件大小 | 395.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-20 20:20:17 | ||
图片预览




文档简介
第2章 综合素质评价
一、选择题(每题3分,共24分)
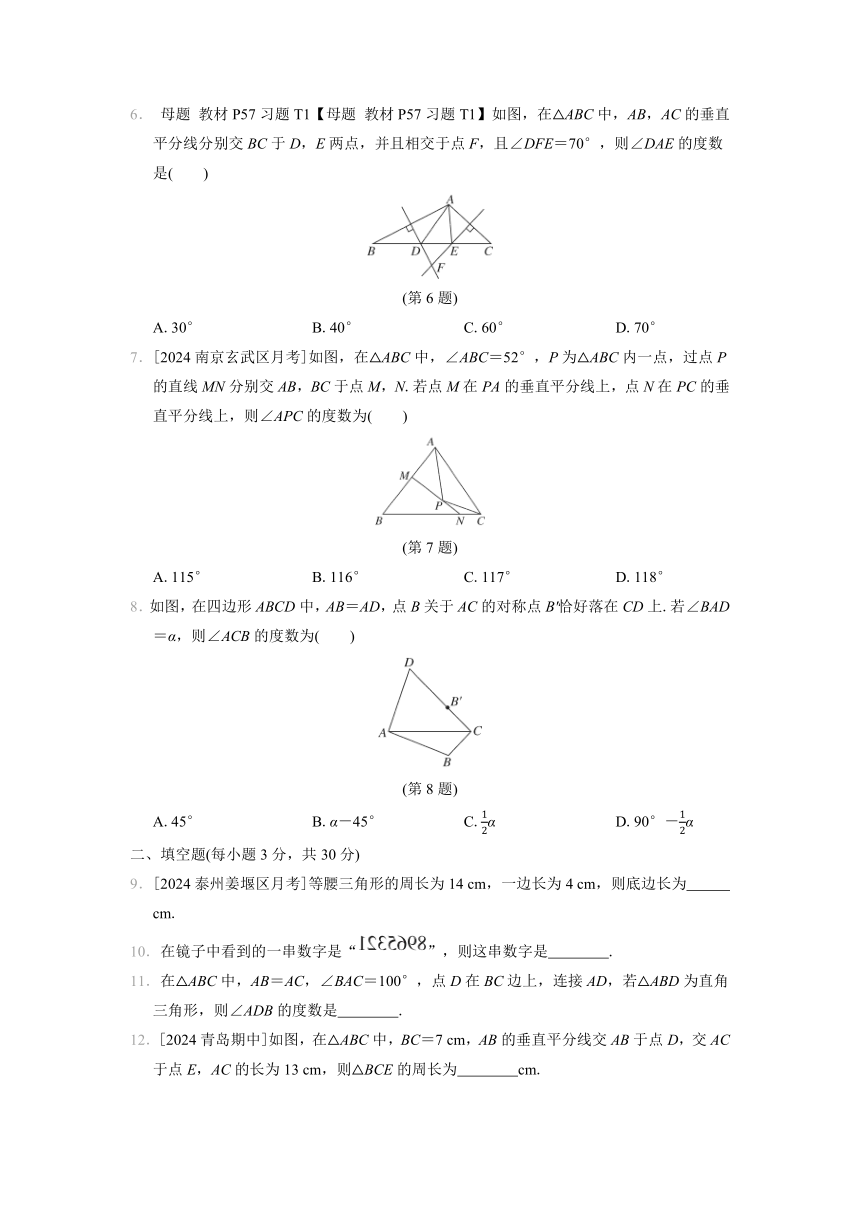
1.【2023·深圳母题·教材P72复习题T1】下列图形中,为轴对称图形的是( )
2.[2024常州二十四中月考]若等腰三角形的底角等于50°,则这个等腰三角形顶角的度数是( )
A.50° B.65° C.80° D.100°
3.[2023贵州]5月26日,“2023中国国际大数据产业博览会”在贵阳开幕,在“自动化立体库”中有许多几何元素,其中有一个等腰三角形模型(示意图如图所示),它的顶角为120°,腰长为12 m,则底边上的高是( )
(第3题)
A.4 m B.6 m C.10 m D.12 m
4.如图,在△ABC中,∠BAC=90°,M是边BC上一点,将△ABC沿AM折叠,点B恰好能与AC的中点D重合.若AB=6,则点M到AB的距离是( )
(第4题)
A.3 B.4 C.5 D.6
5.【母题 教材P72复习题T3(2)】如图,在5×5的小正方形网格中有4个涂阴影的小正方形,它们组成一个轴对称图形.现在移动其中一个小正方形到空白的小正方形处,使得新的4个阴影小正方形组成一个轴对称图形,不同的移法有( )
(第5题)
A.8种 B.12种 C.16种 D.20种
6. 母题 教材P57习题T1【母题 教材P57习题T1】如图,在△ABC中,AB,AC的垂直平分线分别交BC于D,E两点,并且相交于点F,且∠DFE=70°,则∠DAE的度数是( )
(第6题)
A.30° B.40° C.60° D.70°
7.[2024南京玄武区月考]如图,在△ABC中,∠ABC=52°,P为△ABC内一点,过点P的直线MN分别交AB,BC于点M,N.若点M在PA的垂直平分线上,点N在PC的垂直平分线上,则∠APC的度数为( )
(第7题)
A.115° B.116° C.117° D.118°
8.如图,在四边形ABCD中,AB=AD,点B关于AC的对称点B'恰好落在CD上.若∠BAD=α,则∠ACB的度数为( )
(第8题)
A.45° B.α-45° C.α D.90°-α
二、填空题(每小题3分,共30分)
9.[2024泰州姜堰区月考]等腰三角形的周长为14 cm,一边长为4 cm,则底边长为 cm.
10.在镜子中看到的一串数字是“”,则这串数字是 .
11.在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,连接AD,若△ABD为直角三角形,则∠ADB的度数是 .
12.[2024青岛期中]如图,在△ABC中,BC=7 cm,AB的垂直平分线交AB于点D,交AC于点E,AC的长为13 cm,则△BCE的周长为 cm.
(第12题)
13.【新考法 对称法】如图,在Rt△ABC中,∠C=90°,BC<AC.点D,E分别在边AB,BC上,连接DE,将△BDE沿DE折叠,点B的对应点为点B'.若点B'刚好落在边AC上,∠CB'E=30°,CE=3,则BC的长为 .
(第13题)
14.[2024晋中期中]小聪同学在寒假完成项目作业《用纸片“做数学”》时,通过实践探索和推理验证发现,当一张三角形纸片的内角满足一定条件时,这个三角形纸片能沿一条直线裁剪成两个等腰三角形.例如三角形纸片的一个内角是另一个内角的3倍时(如图),沿图中虚线裁剪得到的两个三角形都是等腰三角形.除此情形,三角形纸片的内角条件满足 时,也能沿一条直线裁剪得到两个等腰三角形.(写出一种情况即可)
(第14题)
15.[2023兴化月考]如图,已知O为△ABC三边垂直平分线的交点,∠BAC=70°,则∠BOC= .
(第15题)
16.如图,CD是等边三角形ABC的中线,DE⊥AC,垂足为E.若DE的长为3 cm,则点D到BC的距离为 cm.
(第16题)
17.如图,已知S△ABC=24 m2,AD平分∠BAC,且AD⊥BD于点D,则S△ADC= m2.
(第17题)
18.【新视角 规律探究题】如图所示的是一钢架,设∠AOB=α,为了使钢架更加坚固,需在其内部添加一些钢管EF,FG,GH,…,添加的钢管长度都与OE相等,若最多能添加这样的钢管4根,则α的取值范围是 .
(第18题)
三、解答题(共66分)
19.(10分)两个城镇A,B与两条公路l1,l2的位置如图所示,电信部门需在C处修建一座信号发射塔,要求发射塔到A,B两个城镇的距离相等,到l1,l2两条公路的距离也相等,那么点C应选在何处?请在图中用尺规作图找出点C.(不写已知、求作、作法,只保留作图痕迹)
20.(10分)[2024无锡惠山区月考]如图,在△ABC中,AB=AC,AD为△ABC的角平分线.以点A为圆心,AD长为半径画弧,与AB,AC分别交于点E,F,连接DE,DF.
(1)求证:△ADE≌△ADF;
(2)若AE=4,BD=3,求△ABC的面积.
21.(10分)[2023安徽]如图,在由边长为1个单位长度的小正方形组成的网格中,点A,B,C,D均为格点(网格线的交点).
(1)画出线段AB关于直线CD对称的线段A1B1;
(2)将线段AB先向左平移2个单位长度,再向上平移1个单位长度,得到线段A2B2,画出线段A2B2;
(3)描出线段AB上的点M及直线CD上的点N,使得直线MN垂直平分AB.
22.(12分)[2024南通如东县期末]如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,BE=AC.
(1)求证:AD⊥BC;
(2)若∠BAC=75°,求∠B的度数.
23.(12分)[2024镇江期中]已知:如图,△ABC,△CDE都是等边三角形,AD与BE相交于点O,M,N分别是线段AD,BE的中点.
(1)求证:AD=BE;
(2)求∠DOE的度数;
(3)求证:△MNC是等边三角形.
24.(12分)[2024靖江月考]已知,如图,在△ABC中,AC的垂直平分线与∠ABC的平分线交于点D.
(1)如图①,判断∠BAD和∠BCD之间的数量关系,并说明理由;
(2)如图②,若∠DAC=60°,探究线段AB,BC,BD之间的数量关系,并说明理由;
(3)如图③,在(2)的条件下,DA和CB的延长线交于点E,H是CD上一点且DH=AE,连接AH交BD于点G,若CE=8,求DG的长.(三角形两边的中点连线长等于第三边的一半)
参考答案
一、选择题
1. D 2. C 3. B 4. B 5. D 6. B
7. B 点拨:∵∠ABC=52°,∴∠BMN+∠BNM=128°.∵点M在PA的垂直平分线上,点N在PC的垂直平分线上,∴AM=PM,PN=CN,∴∠MAP=∠MPA,∠CPN=∠PCN.∵∠BMN=∠MAP+∠MPA,∠BNM=∠CPN+∠PCN,∴∠MPA=∠BMN,∠CPN=∠BNM,∴∠MPA+∠CPN=(∠BMN+∠BNM)=×128°=64°,∴∠APC=180°-(∠MPA+∠CPN)=180°-64°=116°.
8. D
二、填空题
9.4或6 10.8965321 11.90°或50°
12.20 13.9 14.有一个内角是直角(答案不唯一)
15.140° 16.3
17.12 点拨:如图,延长BD交AC于点E.∵AD平分∠BAE,AD⊥BD,∴∠BAD=∠EAD,∠ADB=∠ADE=90°.
在△ABD和△AED中,
∴△ABD≌△AED(ASA),∴BD=DE,∴S△ABD=S△ADE,S△BDC=S△CDE,∴S△ABD+S△BDC=S△ADE+S△CDE=S△ADC,∴S△ADC=S△ABC=×24=12(m2).
18.18°≤α<22.5° 点拨:∵OE=EF,∴∠EFO=∠EOF=α,∴∠GEF=∠EOF+∠EFO=2α.同理可得∠GFH=3α,∠HGB=4α.∵最多能添加这样的钢管4根,∴4α<90°,5α≥90°,∴18°≤α<22.5°.
三、解答题
19.解:点C的位置如图所示.
20.(1)证明:∵AD是△ABC的角平分线,
∴∠BAD=∠CAD.由作图知:AE=AF.
在△ADE和△ADF中,
∴△ADE≌△ADF(SAS).
(2)解:∵AB=AC,AD为△ABC的角平分线,
∴AD⊥BC,CD=BD=3,∴BC=6.
又∵AD=AE=4,
∴S△ABC=BC·AD=×6×4=12.
21.解:(1)线段A1B1如图所示.
(2)线段A2B2如图所示.
(3)直线MN即为所求.
22.(1)证明:如图,连接AE.
∵EF垂直平分AB,
∴AE=BE.
又∵BE=AC,
∴AE=AC.
又∵D是CE的中点,∴AD⊥BC.
(2)解:设∠B=x°.∵AE=BE,
∴∠BAE=∠B=x°,∴∠AEC=2x°.
∵AE=AC,∴∠C=∠AEC=2x°.
在△ABC中,∠B+∠C+∠BAC=180°,∴x°+2x°+75°=180°,
解得x=35,∴∠B=35°.
23.(1)证明:∵△ABC,△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE.
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS),∴AD=BE.
(2)解:∵△ACD≌△BCE,∴∠ADC=∠BEC.
∵△DCE是等边三角形,∴∠CED=∠CDE=60°,
∴∠ADE+∠BED=∠ADC+∠CDE+∠BED=∠ADC+60°+∠BED=∠BEC+60°+∠BED=∠CED+60°=60°+60°=120°,
∴∠DOE=180°-(∠ADE+∠BED)=60°.
(3)证明:∵△ACD≌△BCE,∴∠CAD=∠CBE.
∵M,N分别是线段AD,BE的中点,
∴AM=AD,BN=BE,∴AM=BN.
在△ACM和△BCN中,
∴△ACM≌△BCN(SAS),
∴CM=CN,∠ACM=∠BCN,
∵∠ACB=60°,∴∠ACM+∠MCB=60°,
∴∠BCN+∠MCB=60°,即∠MCN=60°,
∴△MNC是等边三角形.
24.解:(1)∠BAD+∠BCD=180°.理由如下:
如图①,过点D作DG⊥BC于点G,DH⊥BA交BA的延长线于点H.
∵AC的垂直平分线与∠ABC的平分线交于点D,
∴AD=CD,∠ABD=∠DBC,
∴DH=DG.
在Rt△ADH和Rt△CDG中,
∴Rt△ADH≌Rt△CDG(HL),
∴∠HAD=∠DCG.
∵∠BAD+∠HAD=180°,∴∠BAD+∠DCG=180°,
即∠BAD+∠BCD=180°.
(2)BD=AB+BC.理由如下:
如图②,在BD上截取BF=AB,连接AF.
由(1)知∠BAD+∠BCD=180°,
∴∠ABC+∠ADC=180°.
∵∠DAC=60°,AD=CD,
∴△ACD为等边三角形,
∴AD=AC,∠ADC=60°,
∴∠ABC=120°,
∴∠ABD=∠DBC=60°.
又∵BF=AB,∴△ABF为等边三角形,
∴AB=AF,∠BAF=60°,∴∠BAF=∠DAC,
∴∠BAF-∠CAF=∠DAC-∠CAF,
即∠BAC=∠DAF.
在△ABC和△AFD中,
∴△ABC≌△AFD(SAS),∴DF=BC,
∴BD=BF+DF=AB+BC.
(3)由(2)知∠DAC=∠DBC=60°.
如图③,延长HD至点M,使DM=DH,连接AM.
由(2)易得∠ACB=∠ADB.
∵DM=DH,DH=AE,
∴DM=AE.
∵∠DAC=∠ADC=60°,
∴∠ADM=∠EAC=120°.
又∵AC=AD,
∴△EAC≌△MDA(SAS),
∴AM=CE,∠MAD=∠ECA,
∴∠MAD=∠ADB,∴DG∥AM.
又∵DH=DM,∴易得AG=GH,
∴DG=AM=CE=4.
一、选择题(每题3分,共24分)
1.【2023·深圳母题·教材P72复习题T1】下列图形中,为轴对称图形的是( )
2.[2024常州二十四中月考]若等腰三角形的底角等于50°,则这个等腰三角形顶角的度数是( )
A.50° B.65° C.80° D.100°
3.[2023贵州]5月26日,“2023中国国际大数据产业博览会”在贵阳开幕,在“自动化立体库”中有许多几何元素,其中有一个等腰三角形模型(示意图如图所示),它的顶角为120°,腰长为12 m,则底边上的高是( )
(第3题)
A.4 m B.6 m C.10 m D.12 m
4.如图,在△ABC中,∠BAC=90°,M是边BC上一点,将△ABC沿AM折叠,点B恰好能与AC的中点D重合.若AB=6,则点M到AB的距离是( )
(第4题)
A.3 B.4 C.5 D.6
5.【母题 教材P72复习题T3(2)】如图,在5×5的小正方形网格中有4个涂阴影的小正方形,它们组成一个轴对称图形.现在移动其中一个小正方形到空白的小正方形处,使得新的4个阴影小正方形组成一个轴对称图形,不同的移法有( )
(第5题)
A.8种 B.12种 C.16种 D.20种
6. 母题 教材P57习题T1【母题 教材P57习题T1】如图,在△ABC中,AB,AC的垂直平分线分别交BC于D,E两点,并且相交于点F,且∠DFE=70°,则∠DAE的度数是( )
(第6题)
A.30° B.40° C.60° D.70°
7.[2024南京玄武区月考]如图,在△ABC中,∠ABC=52°,P为△ABC内一点,过点P的直线MN分别交AB,BC于点M,N.若点M在PA的垂直平分线上,点N在PC的垂直平分线上,则∠APC的度数为( )
(第7题)
A.115° B.116° C.117° D.118°
8.如图,在四边形ABCD中,AB=AD,点B关于AC的对称点B'恰好落在CD上.若∠BAD=α,则∠ACB的度数为( )
(第8题)
A.45° B.α-45° C.α D.90°-α
二、填空题(每小题3分,共30分)
9.[2024泰州姜堰区月考]等腰三角形的周长为14 cm,一边长为4 cm,则底边长为 cm.
10.在镜子中看到的一串数字是“”,则这串数字是 .
11.在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,连接AD,若△ABD为直角三角形,则∠ADB的度数是 .
12.[2024青岛期中]如图,在△ABC中,BC=7 cm,AB的垂直平分线交AB于点D,交AC于点E,AC的长为13 cm,则△BCE的周长为 cm.
(第12题)
13.【新考法 对称法】如图,在Rt△ABC中,∠C=90°,BC<AC.点D,E分别在边AB,BC上,连接DE,将△BDE沿DE折叠,点B的对应点为点B'.若点B'刚好落在边AC上,∠CB'E=30°,CE=3,则BC的长为 .
(第13题)
14.[2024晋中期中]小聪同学在寒假完成项目作业《用纸片“做数学”》时,通过实践探索和推理验证发现,当一张三角形纸片的内角满足一定条件时,这个三角形纸片能沿一条直线裁剪成两个等腰三角形.例如三角形纸片的一个内角是另一个内角的3倍时(如图),沿图中虚线裁剪得到的两个三角形都是等腰三角形.除此情形,三角形纸片的内角条件满足 时,也能沿一条直线裁剪得到两个等腰三角形.(写出一种情况即可)
(第14题)
15.[2023兴化月考]如图,已知O为△ABC三边垂直平分线的交点,∠BAC=70°,则∠BOC= .
(第15题)
16.如图,CD是等边三角形ABC的中线,DE⊥AC,垂足为E.若DE的长为3 cm,则点D到BC的距离为 cm.
(第16题)
17.如图,已知S△ABC=24 m2,AD平分∠BAC,且AD⊥BD于点D,则S△ADC= m2.
(第17题)
18.【新视角 规律探究题】如图所示的是一钢架,设∠AOB=α,为了使钢架更加坚固,需在其内部添加一些钢管EF,FG,GH,…,添加的钢管长度都与OE相等,若最多能添加这样的钢管4根,则α的取值范围是 .
(第18题)
三、解答题(共66分)
19.(10分)两个城镇A,B与两条公路l1,l2的位置如图所示,电信部门需在C处修建一座信号发射塔,要求发射塔到A,B两个城镇的距离相等,到l1,l2两条公路的距离也相等,那么点C应选在何处?请在图中用尺规作图找出点C.(不写已知、求作、作法,只保留作图痕迹)
20.(10分)[2024无锡惠山区月考]如图,在△ABC中,AB=AC,AD为△ABC的角平分线.以点A为圆心,AD长为半径画弧,与AB,AC分别交于点E,F,连接DE,DF.
(1)求证:△ADE≌△ADF;
(2)若AE=4,BD=3,求△ABC的面积.
21.(10分)[2023安徽]如图,在由边长为1个单位长度的小正方形组成的网格中,点A,B,C,D均为格点(网格线的交点).
(1)画出线段AB关于直线CD对称的线段A1B1;
(2)将线段AB先向左平移2个单位长度,再向上平移1个单位长度,得到线段A2B2,画出线段A2B2;
(3)描出线段AB上的点M及直线CD上的点N,使得直线MN垂直平分AB.
22.(12分)[2024南通如东县期末]如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,BE=AC.
(1)求证:AD⊥BC;
(2)若∠BAC=75°,求∠B的度数.
23.(12分)[2024镇江期中]已知:如图,△ABC,△CDE都是等边三角形,AD与BE相交于点O,M,N分别是线段AD,BE的中点.
(1)求证:AD=BE;
(2)求∠DOE的度数;
(3)求证:△MNC是等边三角形.
24.(12分)[2024靖江月考]已知,如图,在△ABC中,AC的垂直平分线与∠ABC的平分线交于点D.
(1)如图①,判断∠BAD和∠BCD之间的数量关系,并说明理由;
(2)如图②,若∠DAC=60°,探究线段AB,BC,BD之间的数量关系,并说明理由;
(3)如图③,在(2)的条件下,DA和CB的延长线交于点E,H是CD上一点且DH=AE,连接AH交BD于点G,若CE=8,求DG的长.(三角形两边的中点连线长等于第三边的一半)
参考答案
一、选择题
1. D 2. C 3. B 4. B 5. D 6. B
7. B 点拨:∵∠ABC=52°,∴∠BMN+∠BNM=128°.∵点M在PA的垂直平分线上,点N在PC的垂直平分线上,∴AM=PM,PN=CN,∴∠MAP=∠MPA,∠CPN=∠PCN.∵∠BMN=∠MAP+∠MPA,∠BNM=∠CPN+∠PCN,∴∠MPA=∠BMN,∠CPN=∠BNM,∴∠MPA+∠CPN=(∠BMN+∠BNM)=×128°=64°,∴∠APC=180°-(∠MPA+∠CPN)=180°-64°=116°.
8. D
二、填空题
9.4或6 10.8965321 11.90°或50°
12.20 13.9 14.有一个内角是直角(答案不唯一)
15.140° 16.3
17.12 点拨:如图,延长BD交AC于点E.∵AD平分∠BAE,AD⊥BD,∴∠BAD=∠EAD,∠ADB=∠ADE=90°.
在△ABD和△AED中,
∴△ABD≌△AED(ASA),∴BD=DE,∴S△ABD=S△ADE,S△BDC=S△CDE,∴S△ABD+S△BDC=S△ADE+S△CDE=S△ADC,∴S△ADC=S△ABC=×24=12(m2).
18.18°≤α<22.5° 点拨:∵OE=EF,∴∠EFO=∠EOF=α,∴∠GEF=∠EOF+∠EFO=2α.同理可得∠GFH=3α,∠HGB=4α.∵最多能添加这样的钢管4根,∴4α<90°,5α≥90°,∴18°≤α<22.5°.
三、解答题
19.解:点C的位置如图所示.
20.(1)证明:∵AD是△ABC的角平分线,
∴∠BAD=∠CAD.由作图知:AE=AF.
在△ADE和△ADF中,
∴△ADE≌△ADF(SAS).
(2)解:∵AB=AC,AD为△ABC的角平分线,
∴AD⊥BC,CD=BD=3,∴BC=6.
又∵AD=AE=4,
∴S△ABC=BC·AD=×6×4=12.
21.解:(1)线段A1B1如图所示.
(2)线段A2B2如图所示.
(3)直线MN即为所求.
22.(1)证明:如图,连接AE.
∵EF垂直平分AB,
∴AE=BE.
又∵BE=AC,
∴AE=AC.
又∵D是CE的中点,∴AD⊥BC.
(2)解:设∠B=x°.∵AE=BE,
∴∠BAE=∠B=x°,∴∠AEC=2x°.
∵AE=AC,∴∠C=∠AEC=2x°.
在△ABC中,∠B+∠C+∠BAC=180°,∴x°+2x°+75°=180°,
解得x=35,∴∠B=35°.
23.(1)证明:∵△ABC,△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE.
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS),∴AD=BE.
(2)解:∵△ACD≌△BCE,∴∠ADC=∠BEC.
∵△DCE是等边三角形,∴∠CED=∠CDE=60°,
∴∠ADE+∠BED=∠ADC+∠CDE+∠BED=∠ADC+60°+∠BED=∠BEC+60°+∠BED=∠CED+60°=60°+60°=120°,
∴∠DOE=180°-(∠ADE+∠BED)=60°.
(3)证明:∵△ACD≌△BCE,∴∠CAD=∠CBE.
∵M,N分别是线段AD,BE的中点,
∴AM=AD,BN=BE,∴AM=BN.
在△ACM和△BCN中,
∴△ACM≌△BCN(SAS),
∴CM=CN,∠ACM=∠BCN,
∵∠ACB=60°,∴∠ACM+∠MCB=60°,
∴∠BCN+∠MCB=60°,即∠MCN=60°,
∴△MNC是等边三角形.
24.解:(1)∠BAD+∠BCD=180°.理由如下:
如图①,过点D作DG⊥BC于点G,DH⊥BA交BA的延长线于点H.
∵AC的垂直平分线与∠ABC的平分线交于点D,
∴AD=CD,∠ABD=∠DBC,
∴DH=DG.
在Rt△ADH和Rt△CDG中,
∴Rt△ADH≌Rt△CDG(HL),
∴∠HAD=∠DCG.
∵∠BAD+∠HAD=180°,∴∠BAD+∠DCG=180°,
即∠BAD+∠BCD=180°.
(2)BD=AB+BC.理由如下:
如图②,在BD上截取BF=AB,连接AF.
由(1)知∠BAD+∠BCD=180°,
∴∠ABC+∠ADC=180°.
∵∠DAC=60°,AD=CD,
∴△ACD为等边三角形,
∴AD=AC,∠ADC=60°,
∴∠ABC=120°,
∴∠ABD=∠DBC=60°.
又∵BF=AB,∴△ABF为等边三角形,
∴AB=AF,∠BAF=60°,∴∠BAF=∠DAC,
∴∠BAF-∠CAF=∠DAC-∠CAF,
即∠BAC=∠DAF.
在△ABC和△AFD中,
∴△ABC≌△AFD(SAS),∴DF=BC,
∴BD=BF+DF=AB+BC.
(3)由(2)知∠DAC=∠DBC=60°.
如图③,延长HD至点M,使DM=DH,连接AM.
由(2)易得∠ACB=∠ADB.
∵DM=DH,DH=AE,
∴DM=AE.
∵∠DAC=∠ADC=60°,
∴∠ADM=∠EAC=120°.
又∵AC=AD,
∴△EAC≌△MDA(SAS),
∴AM=CE,∠MAD=∠ECA,
∴∠MAD=∠ADB,∴DG∥AM.
又∵DH=DM,∴易得AG=GH,
∴DG=AM=CE=4.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
