5.2.2平行线的判定(39张PPT)
文档属性
| 名称 | 5.2.2平行线的判定(39张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 439.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-17 16:01:04 | ||
图片预览


文档简介
课件39张PPT。5.2.2
平行线的判定
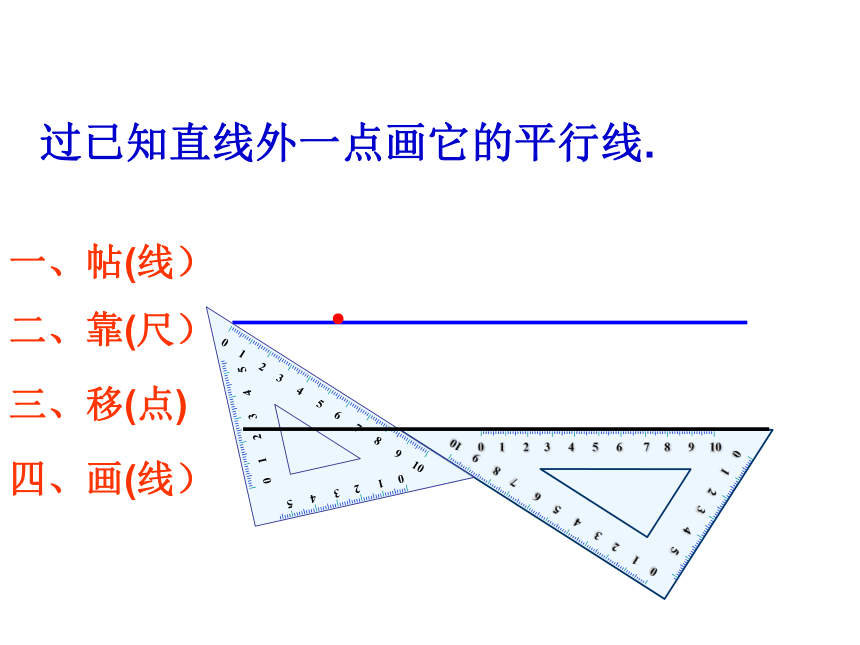
复习提问(1)平面内两条直线的位置关系有几种?(2)怎样过已知直线外一点画已知直线的平行线?相交与平行一、帖(线) 二、靠(尺)三、移(点)四、画(线)过已知直线外一点画它的平行线. 1注意观察!ab.P2如何画平行线?刚才的画法中,三角板起着什么作用?
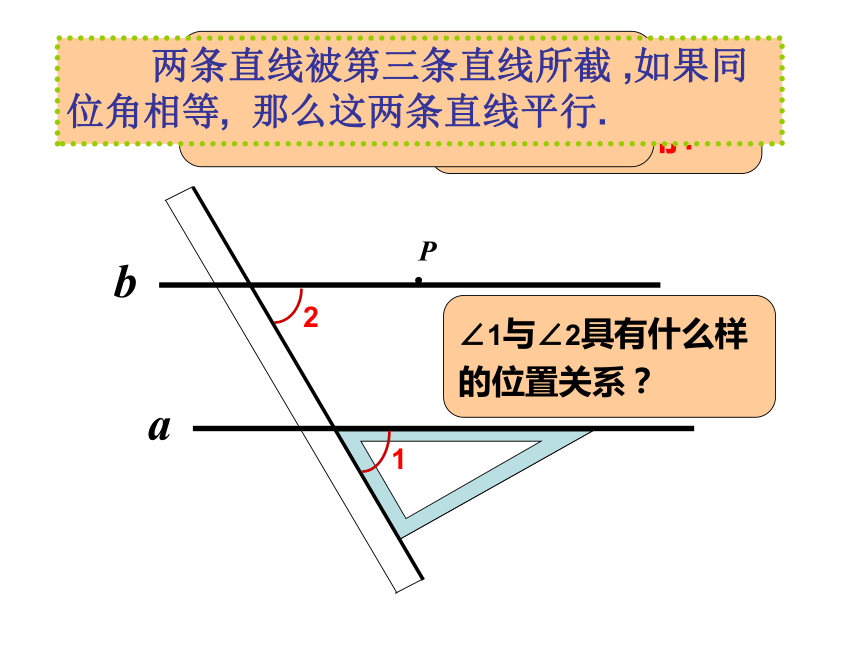
想一想!∠1与∠2具有什么样的位置关系? 我们能得到一个判定两直线平行的方法吗?
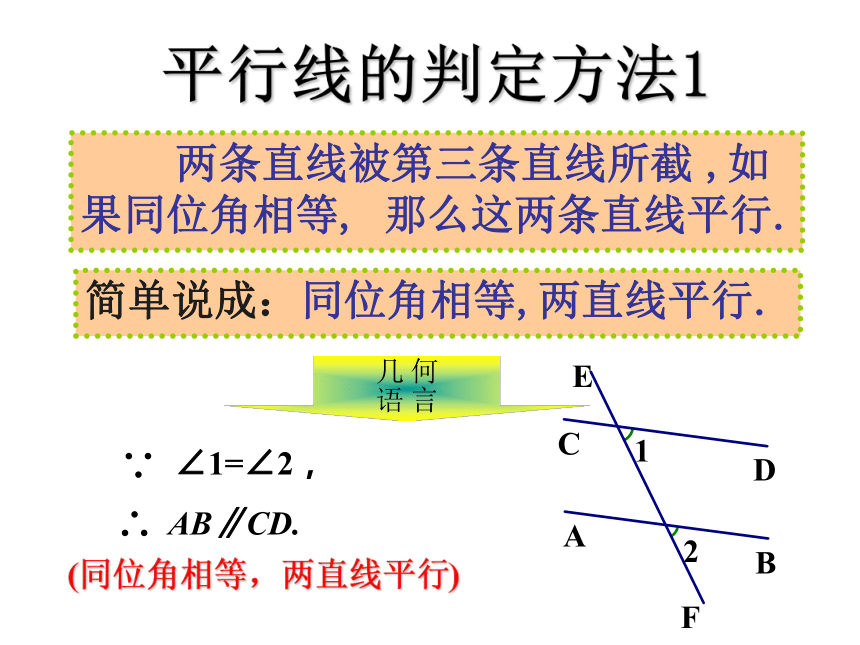
两条直线被第三条直线所截 ,如果同位角相等, 那么这两条直线平行. 两条直线被第三条直线所截 ,如
果同位角相等, 那么这两条直线平行.平行线的判定方法1简单说成:同位角相等,两直线平行.何言
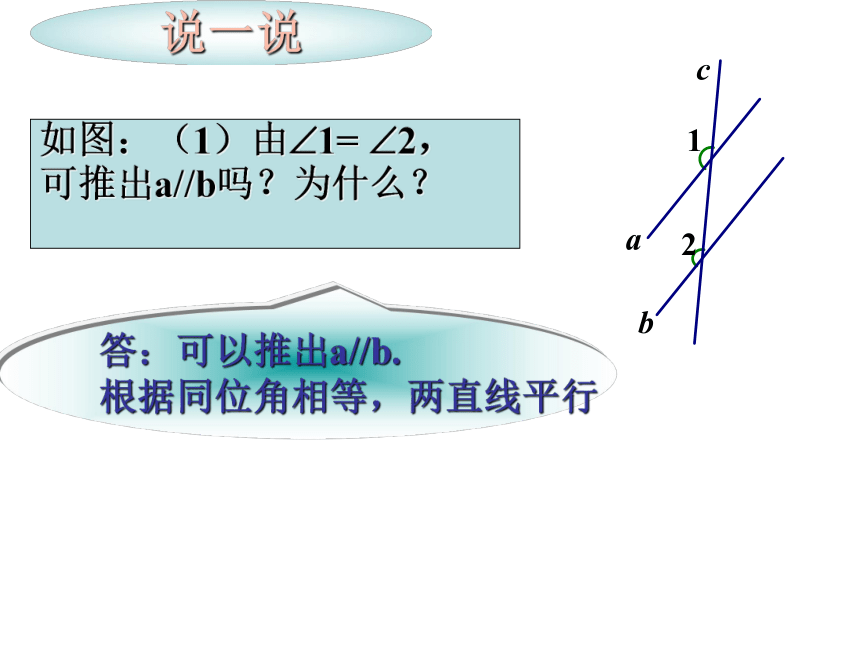
几语(同位角相等,两直线平行)如图:(1)由?1= ?2,
可推出a//b吗?为什么?
说一说答:可以推出a//b.
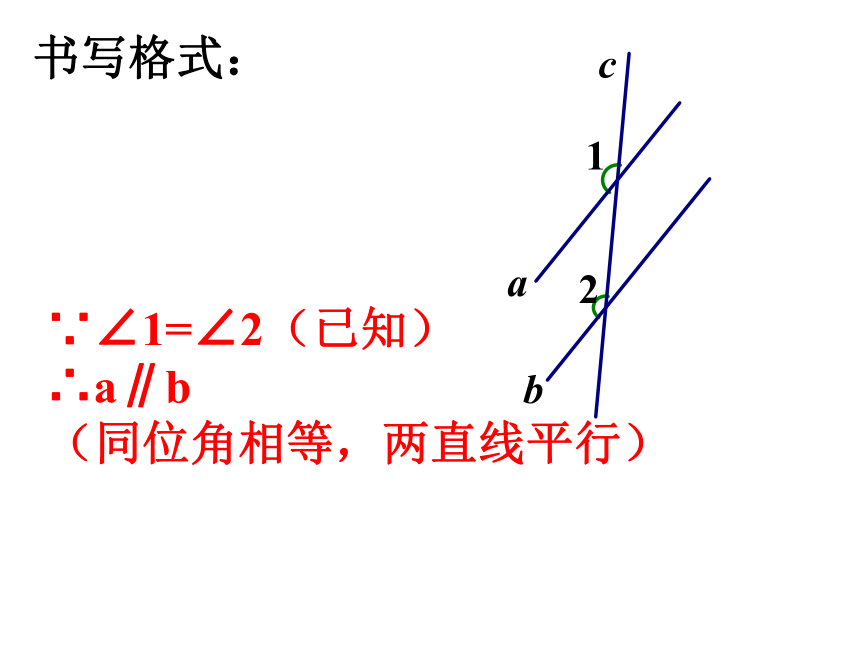
根据同位角相等,两直线平行∵∠1=∠2(已知)
∴a∥b
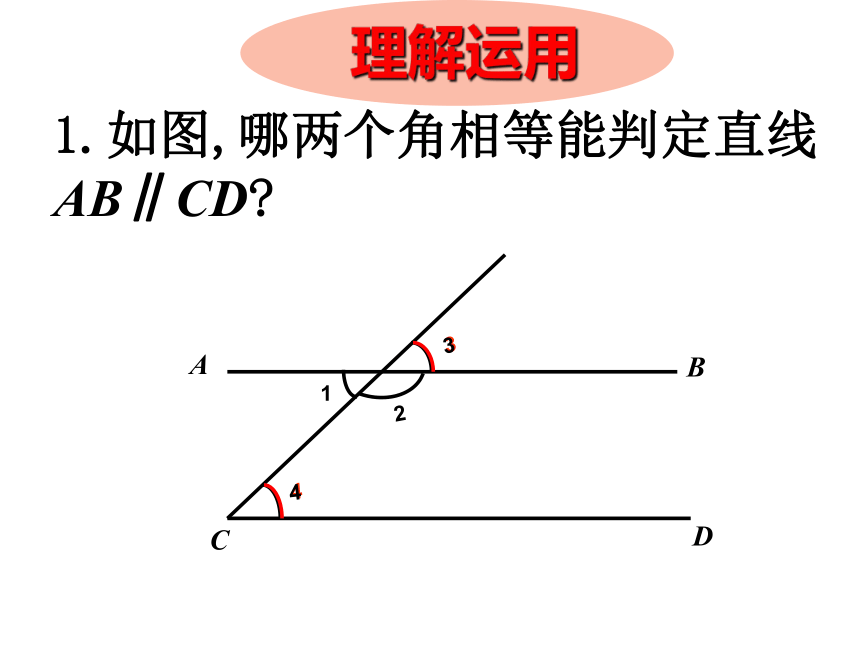
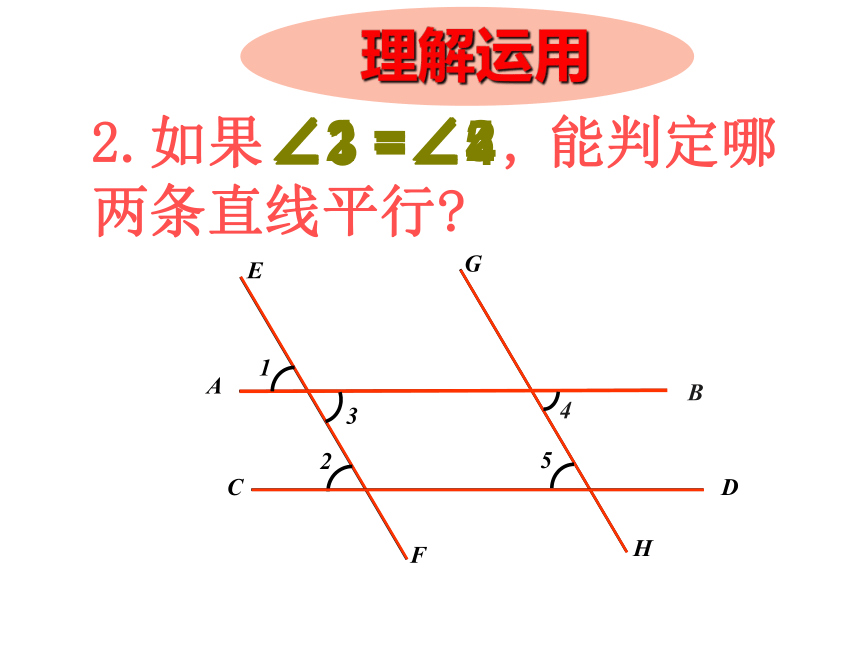
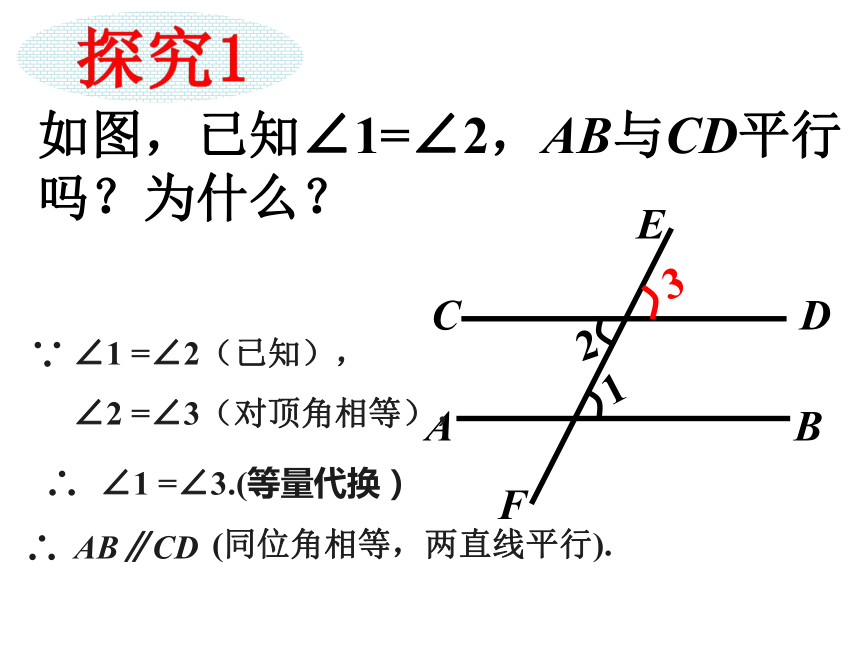
(同位角相等,两直线平行)书写格式:1.如图,哪两个角相等能判定直线AB∥CD?DB1432AC 理解运用 2.如果 , 能判定哪两条直线平行? ∠1 =∠2ABCEFDHG∠3 =∠4∠2 =∠5 理解运用如图,已知∠1=∠2,AB与CD平行吗?为什么?ABCDEF12(同位角相等,两直线平行). 两条直线被第三条直线所截 ,如
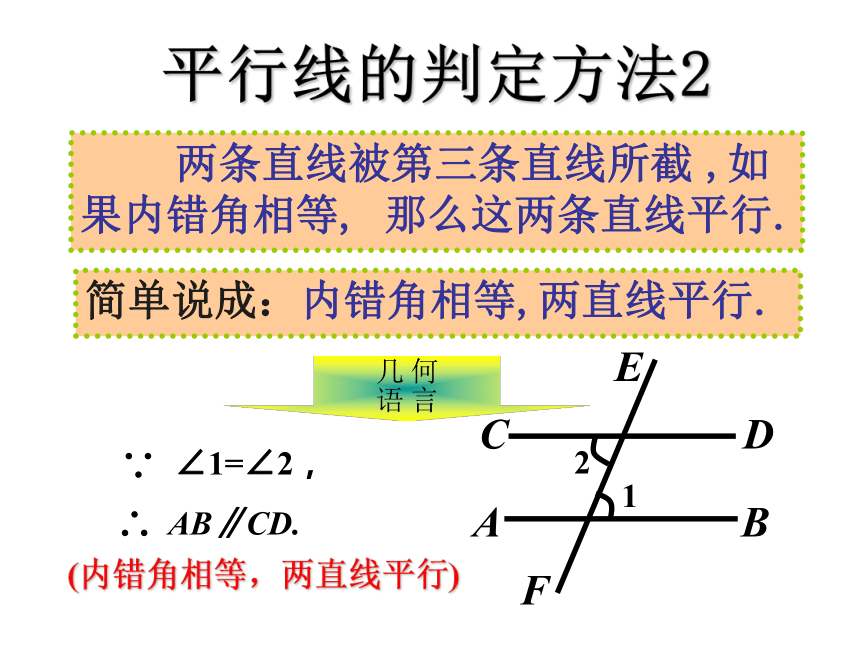
果内错角相等, 那么这两条直线平行.平行线的判定方法2简单说成:内错角相等,两直线平行.何言
几语(内错角相等,两直线平行)如图,∠1= ∠2 ,且∠1=∠3, AB和CD平行吗?
想一想练一练练习:已知:∠1=∠A=∠C,
(1)从∠1=∠A,可以判断哪两条直线平行?它的依据是什么?
(2)从∠1=∠C,可以判断哪两条直线平行?它的依据是什么? 如图,已知∠1+∠2=180°,AB与CD平行吗?为什么?ABCDEF12探究23如图,已知∠1+∠2=180°,AB与CD平行吗?为什么?ABCDEF132探究2 两条直线被第三条直线所截 ,如
果同旁内角互补, 那么这两条直线平行.平行线的判定方法3简单说成:同旁内角互补,两直线平行.何言
几语(同旁内角互补,两直线平行)如图:?B= ? D=45°, ? C=135°,
问图中有哪些直线平行?答:AB//CD,AD//BC ∵? B=45°(已知)
? C=135°(已知)
?? B+ ? C=180°
? AB//CD(同旁内角互补,两直线平行)
同理:AD//BC想一想1.两条直线垂直于同一条直线,这两条
直线平行吗?为什么?
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直意义)
∴b∥c(同位角相等,两直线平行)abc12课堂练习平行线的判定 方法4:在同一平面内,垂直于同一
条直线的两直线互相平行! 判定两条直线平行的方法同位角内错角同旁内角∠1=∠2∠3=∠2∠2+∠4=180°abc1234例题1.① ∵ ∠1 =_____ (已知)
∴ AB∥CE② ∵ ∠2 = (已知)
∴ CD∥BF③ ∵ ∠1 +∠5 =180o(已知)
∴ _____∥_____ABCE∠2∠4(内错角相等,两直线平行)(同位角相等,两直线平行)(同旁内角互补,两直线平行) 已知∠3=45 °,∠1与∠2互余,你能得到 ? 解∵∠1+∠2=90° ∠1=∠2
∴∠1=∠2=45°
∵ ∠3=45°
∴∠ 2=∠3
∴ AB∥CD(内错角相等,两直线平行)AB//CD例题2应用练习1.如图,如果∠3=∠7,那么 _____∥_____,理由是__________ ;如果∠5=∠3,那么_____∥_____,理由是__________ ;如果∠2+∠5= ______°,那么 ∥ ,理由是__________ .abab同位角相等,两直线平行内错角相等,两直线平行180ab同旁内角互补,两直线平行2、如图,∠1=∠2,则下列结论正确的是( )(A)AD//BC (B)AB//CD
(C)AD//EF (D)EF//BCC应用练习应用练习 A4、如图,哪些直线平行,哪些直线不平行? 与 平行, 与 不平行应用练习5.如图:可以确定AB∥CE的条件是( )
A.∠2=∠B
B. ∠1=∠A
C. ∠3=∠B
D. ∠3=∠AC应用练习6.如图,已知∠1=30°,∠2或 ∠3
满足条件___________,则a//b∠2=150 或∠3=30°__________//.18076)4(;14)3(;63)2(;21)1(0的条件序号是其中能识别所截,给出下列条件:被直线 、7.直线bacba=D+DD=DD=DD=D(1)(2)(4)同位角相等内错角相等同旁内角互补两直线平行平行线的判定示意图判定数量关系位置关系小结
(1)从∠1=∠2,可以推出 ∥ ,
理由是 。
(2)从∠2=∠ ,可以推出c∥d ,
理由是 。
(3)如果∠1=75°,∠4=105°,
可以推出 ∥ 。
理由是 。练一练ba内错角相等,两直线平行同位角相等,两直线平行3ab42cd31ab同旁内角互补,两直线平行1.如图从∠1=∠4,可以推出 ∥ ,
理由是 。(2)从∠ABC +∠ =180,可以推出AB∥CD ,
理由是 。(3)从∠ =∠ ,可以推出AD∥BC,
理由是 。(4)从∠5=∠ ,可以推出AB∥CD,
理由是 。练一练AB内错角相等,两直线平行CDBCD同旁内角互补,两直线平行23内错角相等,两直线平行ABC同位角相等,两直线平行2.如图 如图,∠1=∠2,能判断AB∥DF吗?为什么?
若不能判断AB∥DF,你认为还需要再添加的一个条件是什么呢?写出这个条件,并说明你的理由。
?
?
?
?
?
?不能.添加∠CBD=∠EDB内错角相等,两直线平行想想还可以添加什么条件?体验成功——达标检测B必做题:
1、如果∠A +∠B =180°,那么根据同旁内
角互补,两直线平行,可得_____∥_____;
如果 +∠B =180°,那么根据同旁内角
互补,两直线平行,可得AB∥EC。 AE BC6161∠C终极挑战1.下列说法错误的是( )
A.同位角不一定相等 B.内错角都相等
C.同旁内角互补 D.同位角相等,两直线平行。
2. .如图所示,如果∠D=∠EFC,那么( )
A.AD∥BC B.EF∥BC C.AB∥DC D.AD∥EF
3.在同一平面内,若直线a,b,c满足a⊥b,a⊥c,则b与c的位置关系是______. 第2题DDb∥c4.如图1所示,下列条件中,能判断AB∥CD的是( )
A.∠BAD=∠BCD B.∠1=∠2; C.∠3=∠4 D.∠BAC=∠ACD
(1) (2)
5.如图2所示,如果∠D=∠EFC,那么( )
A.AD∥BC B.EF∥BC C.AB∥DC D.AD∥EF
6.如图3所示,能判断AB∥CE的条件是( )
A.∠A=∠ACE B.∠A=∠ECD C.∠B=∠BCA D.∠B=∠ACE
(3)
7.下列说法错误的是( )
A.同位角不一定相等 B.内错角都相等
C.同旁内角可能相等 D.同旁内角互补,两直线平行
8.不相邻的两个直角,如果它们有一边在同一直线上,那么另一边相互( )
A.平行 B.垂直 C.平行或垂直 D.平行或垂直或相交
9.如图,根据下列条件可判断哪两条直线平行,并说明理由。
(1)∠1=∠2 (2)∠3=∠A
(3)∠A+∠2+∠4=180°
终极挑战课后作业: 课本179页3、4题; 祝同学们学习进步再见
平行线的判定
复习提问(1)平面内两条直线的位置关系有几种?(2)怎样过已知直线外一点画已知直线的平行线?相交与平行一、帖(线) 二、靠(尺)三、移(点)四、画(线)过已知直线外一点画它的平行线. 1注意观察!ab.P2如何画平行线?刚才的画法中,三角板起着什么作用?
想一想!∠1与∠2具有什么样的位置关系? 我们能得到一个判定两直线平行的方法吗?
两条直线被第三条直线所截 ,如果同位角相等, 那么这两条直线平行. 两条直线被第三条直线所截 ,如
果同位角相等, 那么这两条直线平行.平行线的判定方法1简单说成:同位角相等,两直线平行.何言
几语(同位角相等,两直线平行)如图:(1)由?1= ?2,
可推出a//b吗?为什么?
说一说答:可以推出a//b.
根据同位角相等,两直线平行∵∠1=∠2(已知)
∴a∥b
(同位角相等,两直线平行)书写格式:1.如图,哪两个角相等能判定直线AB∥CD?DB1432AC 理解运用 2.如果 , 能判定哪两条直线平行? ∠1 =∠2ABCEFDHG∠3 =∠4∠2 =∠5 理解运用如图,已知∠1=∠2,AB与CD平行吗?为什么?ABCDEF12(同位角相等,两直线平行). 两条直线被第三条直线所截 ,如
果内错角相等, 那么这两条直线平行.平行线的判定方法2简单说成:内错角相等,两直线平行.何言
几语(内错角相等,两直线平行)如图,∠1= ∠2 ,且∠1=∠3, AB和CD平行吗?
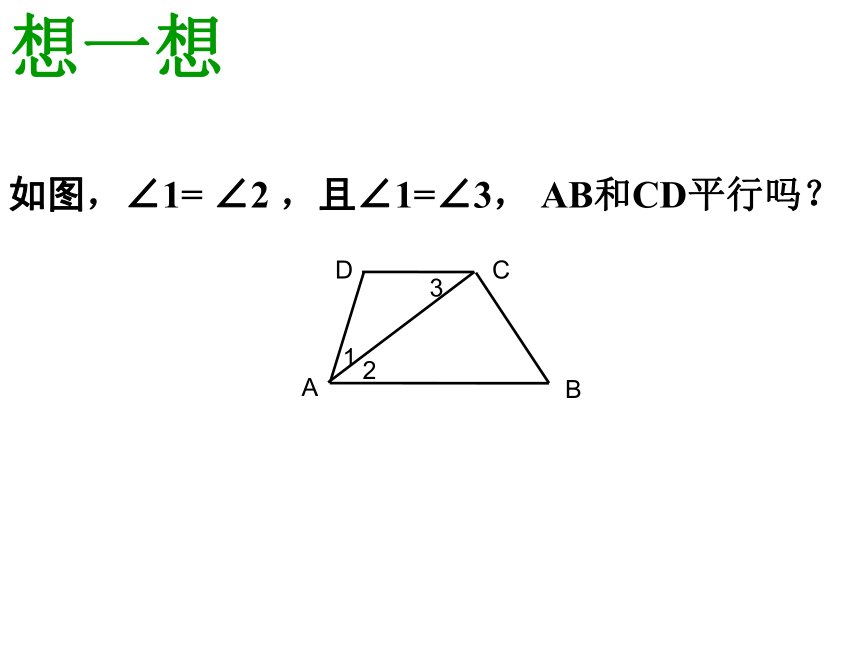
想一想练一练练习:已知:∠1=∠A=∠C,
(1)从∠1=∠A,可以判断哪两条直线平行?它的依据是什么?
(2)从∠1=∠C,可以判断哪两条直线平行?它的依据是什么? 如图,已知∠1+∠2=180°,AB与CD平行吗?为什么?ABCDEF12探究23如图,已知∠1+∠2=180°,AB与CD平行吗?为什么?ABCDEF132探究2 两条直线被第三条直线所截 ,如
果同旁内角互补, 那么这两条直线平行.平行线的判定方法3简单说成:同旁内角互补,两直线平行.何言
几语(同旁内角互补,两直线平行)如图:?B= ? D=45°, ? C=135°,
问图中有哪些直线平行?答:AB//CD,AD//BC ∵? B=45°(已知)
? C=135°(已知)
?? B+ ? C=180°
? AB//CD(同旁内角互补,两直线平行)
同理:AD//BC想一想1.两条直线垂直于同一条直线,这两条
直线平行吗?为什么?
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直意义)
∴b∥c(同位角相等,两直线平行)abc12课堂练习平行线的判定 方法4:在同一平面内,垂直于同一
条直线的两直线互相平行! 判定两条直线平行的方法同位角内错角同旁内角∠1=∠2∠3=∠2∠2+∠4=180°abc1234例题1.① ∵ ∠1 =_____ (已知)
∴ AB∥CE② ∵ ∠2 = (已知)
∴ CD∥BF③ ∵ ∠1 +∠5 =180o(已知)
∴ _____∥_____ABCE∠2∠4(内错角相等,两直线平行)(同位角相等,两直线平行)(同旁内角互补,两直线平行) 已知∠3=45 °,∠1与∠2互余,你能得到 ? 解∵∠1+∠2=90° ∠1=∠2
∴∠1=∠2=45°
∵ ∠3=45°
∴∠ 2=∠3
∴ AB∥CD(内错角相等,两直线平行)AB//CD例题2应用练习1.如图,如果∠3=∠7,那么 _____∥_____,理由是__________ ;如果∠5=∠3,那么_____∥_____,理由是__________ ;如果∠2+∠5= ______°,那么 ∥ ,理由是__________ .abab同位角相等,两直线平行内错角相等,两直线平行180ab同旁内角互补,两直线平行2、如图,∠1=∠2,则下列结论正确的是( )(A)AD//BC (B)AB//CD
(C)AD//EF (D)EF//BCC应用练习应用练习 A4、如图,哪些直线平行,哪些直线不平行? 与 平行, 与 不平行应用练习5.如图:可以确定AB∥CE的条件是( )
A.∠2=∠B
B. ∠1=∠A
C. ∠3=∠B
D. ∠3=∠AC应用练习6.如图,已知∠1=30°,∠2或 ∠3
满足条件___________,则a//b∠2=150 或∠3=30°__________//.18076)4(;14)3(;63)2(;21)1(0的条件序号是其中能识别所截,给出下列条件:被直线 、7.直线bacba=D+DD=DD=DD=D(1)(2)(4)同位角相等内错角相等同旁内角互补两直线平行平行线的判定示意图判定数量关系位置关系小结
(1)从∠1=∠2,可以推出 ∥ ,
理由是 。
(2)从∠2=∠ ,可以推出c∥d ,
理由是 。
(3)如果∠1=75°,∠4=105°,
可以推出 ∥ 。
理由是 。练一练ba内错角相等,两直线平行同位角相等,两直线平行3ab42cd31ab同旁内角互补,两直线平行1.如图从∠1=∠4,可以推出 ∥ ,
理由是 。(2)从∠ABC +∠ =180,可以推出AB∥CD ,
理由是 。(3)从∠ =∠ ,可以推出AD∥BC,
理由是 。(4)从∠5=∠ ,可以推出AB∥CD,
理由是 。练一练AB内错角相等,两直线平行CDBCD同旁内角互补,两直线平行23内错角相等,两直线平行ABC同位角相等,两直线平行2.如图 如图,∠1=∠2,能判断AB∥DF吗?为什么?
若不能判断AB∥DF,你认为还需要再添加的一个条件是什么呢?写出这个条件,并说明你的理由。
?
?
?
?
?
?不能.添加∠CBD=∠EDB内错角相等,两直线平行想想还可以添加什么条件?体验成功——达标检测B必做题:
1、如果∠A +∠B =180°,那么根据同旁内
角互补,两直线平行,可得_____∥_____;
如果 +∠B =180°,那么根据同旁内角
互补,两直线平行,可得AB∥EC。 AE BC6161∠C终极挑战1.下列说法错误的是( )
A.同位角不一定相等 B.内错角都相等
C.同旁内角互补 D.同位角相等,两直线平行。
2. .如图所示,如果∠D=∠EFC,那么( )
A.AD∥BC B.EF∥BC C.AB∥DC D.AD∥EF
3.在同一平面内,若直线a,b,c满足a⊥b,a⊥c,则b与c的位置关系是______. 第2题DDb∥c4.如图1所示,下列条件中,能判断AB∥CD的是( )
A.∠BAD=∠BCD B.∠1=∠2; C.∠3=∠4 D.∠BAC=∠ACD
(1) (2)
5.如图2所示,如果∠D=∠EFC,那么( )
A.AD∥BC B.EF∥BC C.AB∥DC D.AD∥EF
6.如图3所示,能判断AB∥CE的条件是( )
A.∠A=∠ACE B.∠A=∠ECD C.∠B=∠BCA D.∠B=∠ACE
(3)
7.下列说法错误的是( )
A.同位角不一定相等 B.内错角都相等
C.同旁内角可能相等 D.同旁内角互补,两直线平行
8.不相邻的两个直角,如果它们有一边在同一直线上,那么另一边相互( )
A.平行 B.垂直 C.平行或垂直 D.平行或垂直或相交
9.如图,根据下列条件可判断哪两条直线平行,并说明理由。
(1)∠1=∠2 (2)∠3=∠A
(3)∠A+∠2+∠4=180°
终极挑战课后作业: 课本179页3、4题; 祝同学们学习进步再见
