【沪科版八上同步练习】 15.2线段的垂直平分线(含答案)
文档属性
| 名称 | 【沪科版八上同步练习】 15.2线段的垂直平分线(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 11.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-20 23:40:07 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
【沪科版八上同步练习】
15.2线段的垂直平分线
一、单选题
1.如图,△ABC中,DE是AC的垂直平分线,AE= 5cm,△ABD的周长为16cm,则△ABC的周长为( )
A.21cm B.26cm C.28cm D.31cm
2.如图,在中,分别以A,B为圆心,大于的长度为半径画弧,两弧相交于点P和点O,作直线交于点E,交于点D,若,,则的周长为( )
A.9 B. C.13 D.18
3.如图,三个小朋友相约周末出去玩,图中点A、B、C代表三人的家所在的位置,为公平起见,集合地应定在以下什么位置,可以使三个小朋友的家到集合地的距离相等?( )
A.在三条高线所在的直线的交点处
B.在三条中线的交点处
C.在三条边的垂直平分线的交点处
D.在三条角平分线的交点处
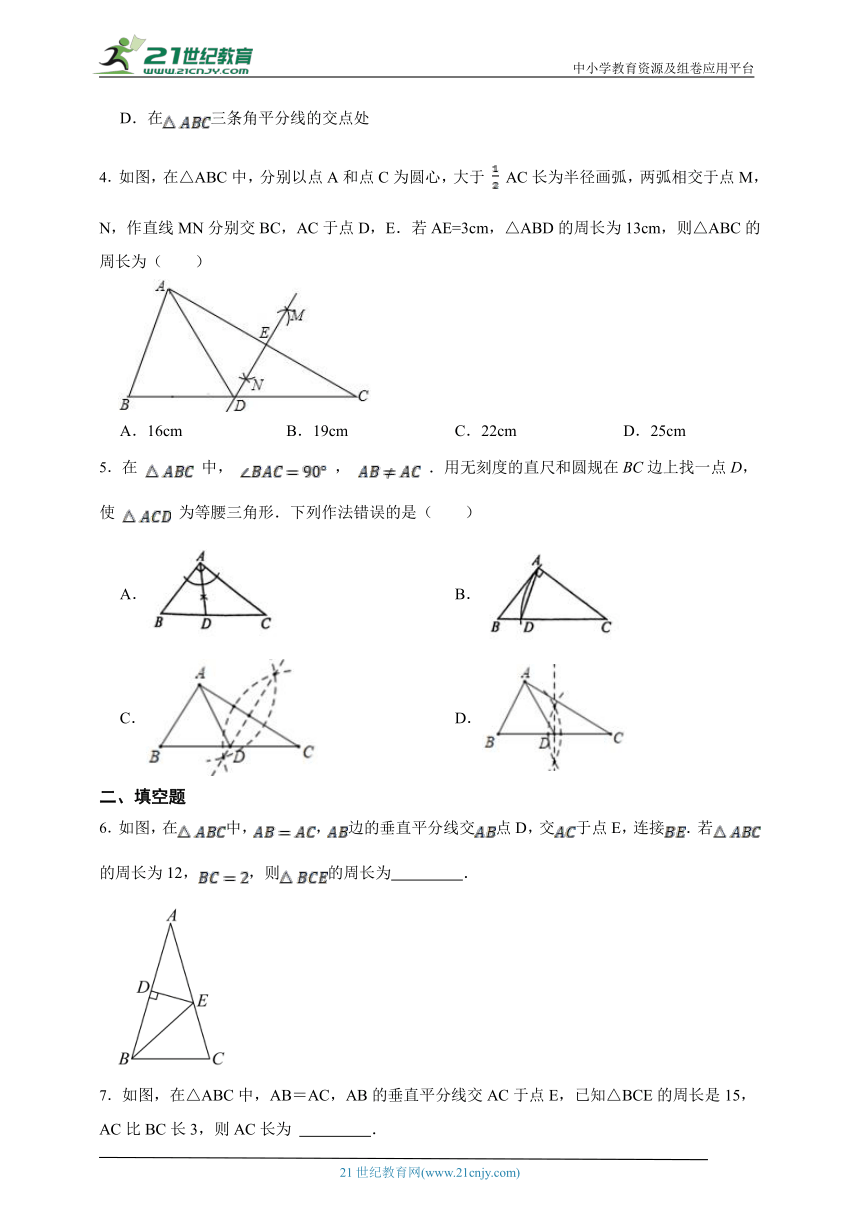
4.如图,在△ABC中,分别以点A和点C为圆心,大于 AC长为半径画弧,两弧相交于点M,N,作直线MN分别交BC,AC于点D,E.若AE=3cm,△ABD的周长为13cm,则△ABC的周长为( )
A.16cm B.19cm C.22cm D.25cm
5.在 中, , .用无刻度的直尺和圆规在BC边上找一点D,使 为等腰三角形.下列作法错误的是( )
A. B.
C. D.
二、填空题
6.如图,在中,,边的垂直平分线交点D,交于点E,连接.若的周长为12,,则的周长为 .
7.如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,已知△BCE的周长是15,AC比BC长3,则AC长为 .
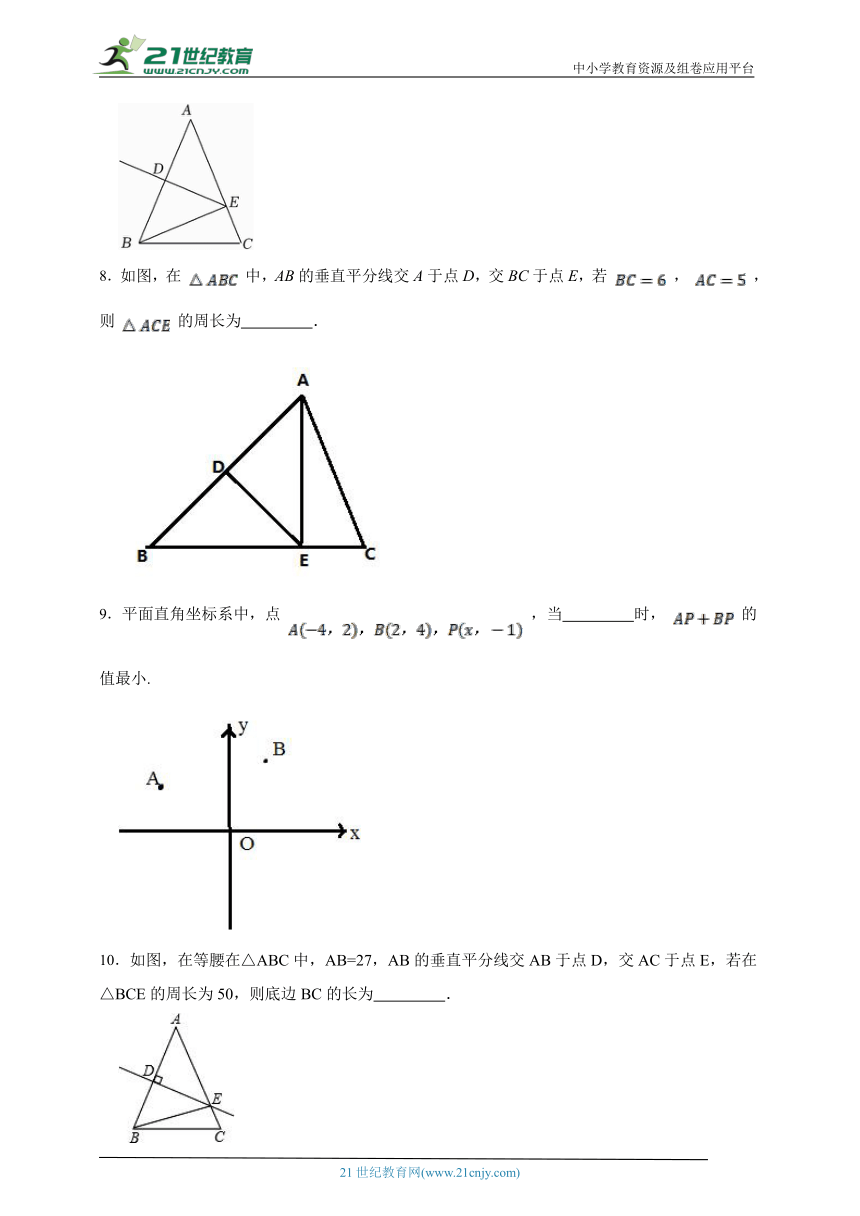
8.如图,在 中,AB的垂直平分线交A于点D,交BC于点E,若 , ,则 的周长为 .
9.平面直角坐标系中,点 ,当 时, 的值最小.
10.如图,在等腰在△ABC中,AB=27,AB的垂直平分线交AB于点D,交AC于点E,若在△BCE的周长为50,则底边BC的长为 .
11.在 中,边 、 的垂直平分线分别交边 于点 、点 , ,则 °.
三、计算题
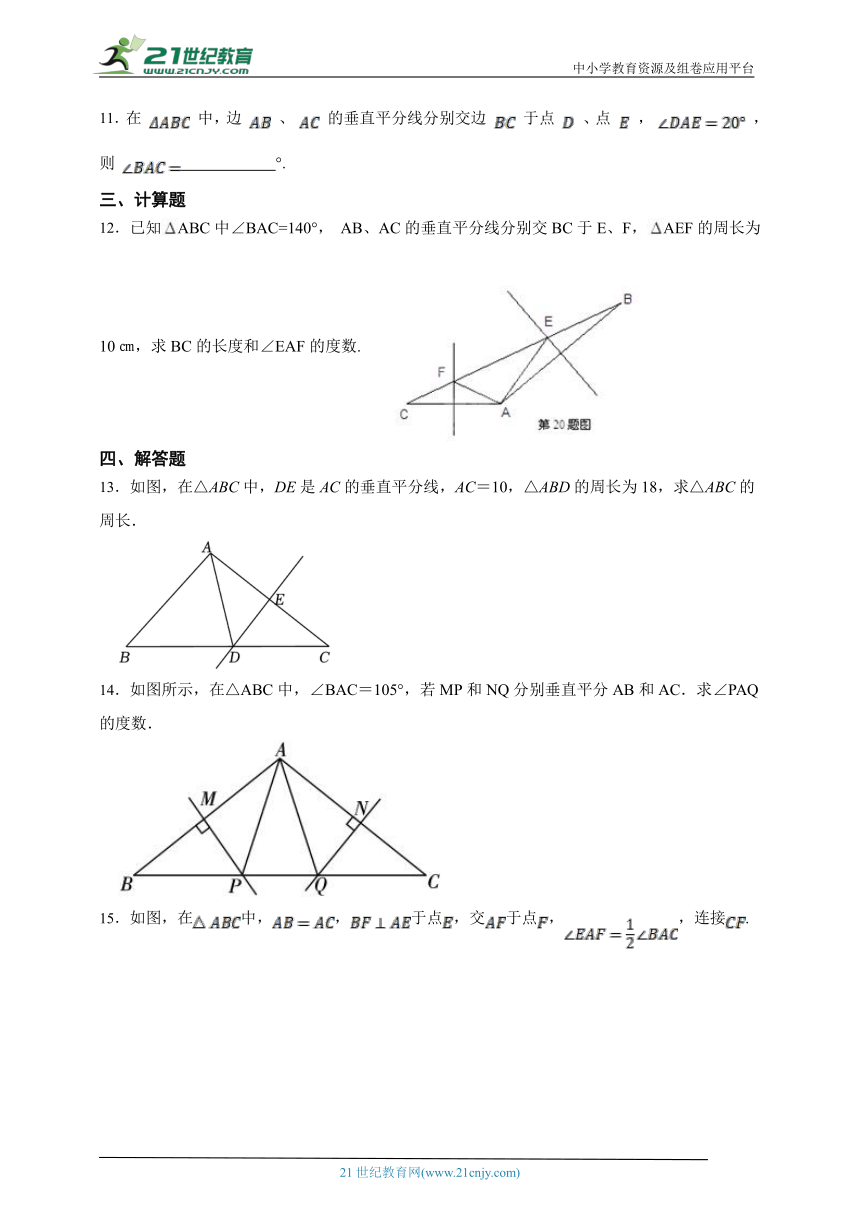
12.已知ABC中∠BAC=140°, AB、AC的垂直平分线分别交BC于E、F,AEF的周长为10㎝,求BC的长度和∠EAF的度数.
四、解答题
13.如图,在△ABC中,DE是AC的垂直平分线,AC=10,△ABD的周长为18,求△ABC的周长.
14.如图所示,在△ABC中,∠BAC=105°,若MP和NQ分别垂直平分AB和AC.求∠PAQ的度数.
15.如图,在中,,于点,交于点,,连接.
(1)如图1,当在内部时,求证:;
(2)如图2,当的边,分别在外部和内部时,求证:.
五、综合题
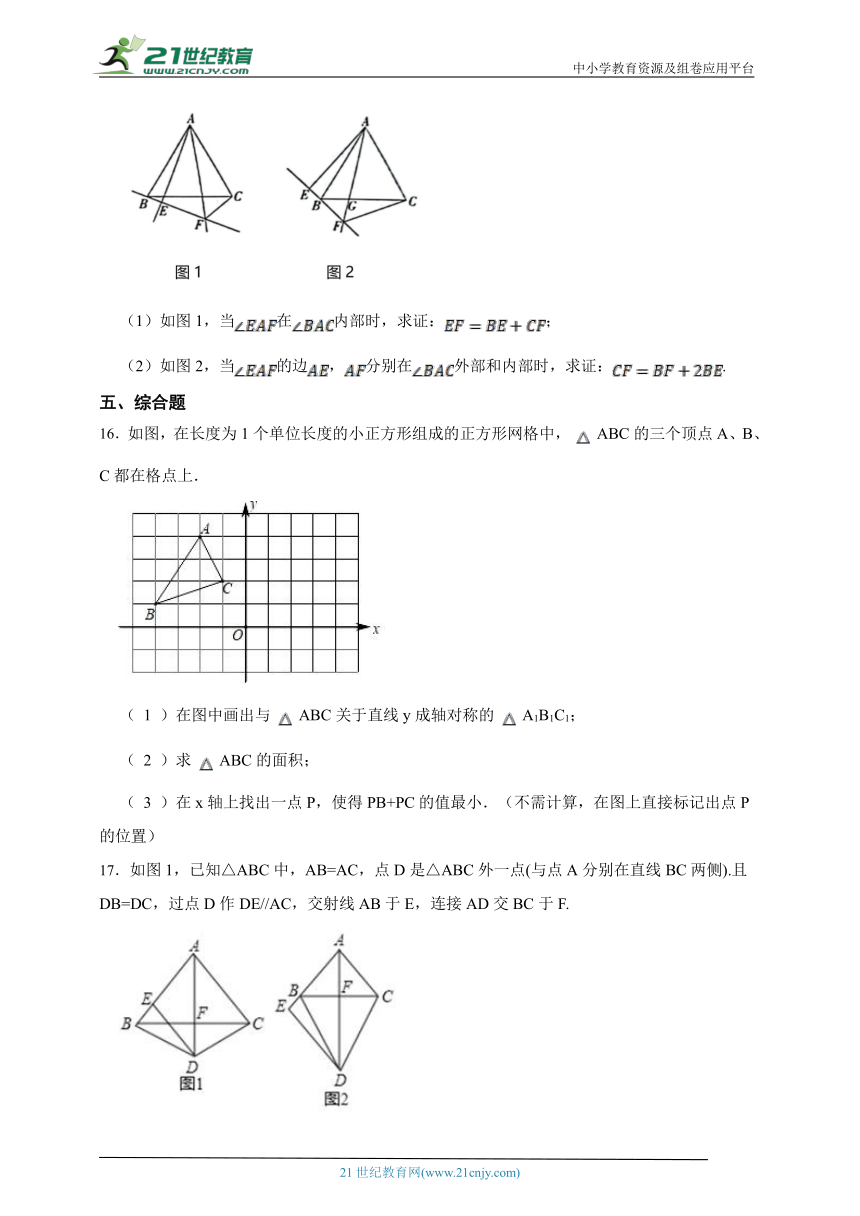
16.如图,在长度为1个单位长度的小正方形组成的正方形网格中, ABC的三个顶点A、B、C都在格点上.
( 1 )在图中画出与 ABC关于直线y成轴对称的 A1B1C1;
( 2 )求 ABC的面积;
( 3 )在x轴上找出一点P,使得PB+PC的值最小.(不需计算,在图上直接标记出点P的位置)
17.如图1,已知△ABC中,AB=AC,点D是△ABC外一点(与点A分别在直线BC两侧).且DB=DC,过点D作DE//AC,交射线AB于E,连接AD交BC于F.
(1)求证:AD垂直BC;
(2)如图1,点E在线段AB上且不与B重合时,求证:DE=AE;
(3)如图2,当点E在线段AB的延长线上时,请直接写出线段DE,AC,BE的数量关系.
18.如图,一次函数 的图象分别与 轴和 轴交于 , 两点,且与正比例函数 的图象交于点 .
(1)求 的值;
(2)求正比例函数的表达式;
(3)点 是一次函数图象上的一点,且 的面积是3,求点 的坐标;
(4)在 轴上是否存在点 ,使 的值最小?若存在,求出点 的坐标,若不存在,说明理由.
六、实践探究题
19.如何设计与制作风筝呢?请同学们阅读“勤学小组”的项目实施过程,帮助他们解决项目实施过程中遇到的问题。
项目主题:设计与制作风筝.
项目实施:
(1)任务一:了解风筝:“勤学小组”的同学查阅了有关风筝的历史,种类,结构,制作等方面的资料,同时还收集到如图的风筝图案,请你帮助他们从中选出不是轴对称图形的风筝图案
(2)任务二:设计风筝:设计风筝时主要进行风筝面与风筝骨架的设计.“勤学小组”的同学设计好了风筝面,接下来在正方形网格中进行风筝骨架的设计,请你帮助他们以直线l为对称轴画出风筝骨架的另一半.
(3)任务三:制作风筝:传统风筝的技艺概括起来四个字:扎、糊、绘、放,简称“四艺”.“勒学小组”的同学准备用竹条扎制如图所示的风筝骨架,已知AD⊥BC于点D, BD=CD,AB=60cm,则竹条AC的长为 cm.
(4)任务四:放飞风筝:同学们拿着自己设计与制作的风筝进行了试飞,并根据试飞结果对风筝进行了修改完善.
项目反思:同学们对项目学习的整个过程进行反思,并编写了“简易风筝制作说明书”。请你写出一条在项目实施的过程中用到的数学知识
答案解析部分
1.【答案】B
【知识点】线段垂直平分线的性质
2.【答案】C
【知识点】线段垂直平分线的性质;尺规作图-垂直平分线
3.【答案】C
【知识点】线段垂直平分线的性质
4.【答案】B
【知识点】线段垂直平分线的性质
5.【答案】A
【知识点】尺规作图-垂直平分线
6.【答案】7
【知识点】线段垂直平分线的性质
7.【答案】9
【知识点】线段垂直平分线的性质
8.【答案】11
【知识点】线段垂直平分线的性质
9.【答案】
【知识点】待定系数法求一次函数解析式;轴对称的应用-最短距离问题
10.【答案】23
【知识点】线段垂直平分线的性质
11.【答案】80或100
【知识点】三角形内角和定理;线段垂直平分线的性质
12.【答案】解:∵AB、AC的垂直平分线分别交BC于E、F,
∴AE=BE,AF=CF;
∵△AEF周长为:AE+EF+AF=BE+EF+CF=BC=10㎝,
∴BC=10㎝,
又∵AB、AC的垂直平分线分别交BC于E、F,
∴AE=BE,AF=CF,
∴∠B=∠BAE,∠C=∠CAF,
∵△ABC中,∠BAC=140°,
∴∠B+∠C=180°-∠BAC=40°,
∴∠BAE+∠CAF=40°,
∴∠EAF=∠BAC-(∠BAE+∠CAF)=140°-40°=100°。
【知识点】三角形内角和定理;线段垂直平分线的性质
13.【答案】解:∵DE是AC的垂直平分线,
∴AD=CD,
∵△ABD得周长为18,
∴AB+BD+AD=18,
∴AB+BD+CD=AB+BC=18,
∴△ABC得周长为AB+BC+AC=28.
【知识点】线段垂直平分线的性质
14.【答案】解:∵MP为AB的垂直平分线,
∴PA=PB,
∴∠B=∠PAB,
同理∠C=∠QAC,
∴∠B+∠C=∠PAB+∠QAC,
∵∠B+∠C=180°-∠BAC=180°-105°=75°,
∴∠PAB+∠QAC=75°,
∴∠PAQ=∠BAC-(∠PAB+∠QAC)
=105°-75°
=30°.
【知识点】三角形内角和定理;线段垂直平分线的性质
15.【答案】(1)证明:如图,在上截取,连接.
∵,
∴,.
又∵,
∴.
∵,
∴.
∴.
∴.
在和中,
∴.
∴.
∴.
(2)证明:如图,在的延长线上截取,连接.
∵,
∴,.
又∵,
∴.
∵,
∴.
∴.
∴.
在和中,
∴.
∴.
∵,
∴.
【知识点】三角形全等及其性质;线段垂直平分线的性质;三角形全等的判定-SAS;线段的和、差、倍、分的简单计算
16.【答案】解:(1)如图所示,△A1B1C1即为所求;
(2)△ABC的面积=3×3﹣ ×2×3﹣ ×1×2﹣ ×1×3= ;
(3)如图所示,点P即为所求.
【知识点】三角形的面积;作图﹣轴对称;轴对称的应用-最短距离问题
17.【答案】(1)证明:∵AB=AC
∴点A在线段BC的垂直平分线上,
∵DB=DC
∴点D在线段BC的垂直平分线上,
∴直线AD是BC的垂直平分线,
∴AD垂直BC;
(2)解:∵AB=AC,AD⊥BC
∴∠BAD=∠CAD
∵DE∥AC
∴∠EDA=∠CAD
∴∠BAD=∠EDA
∴DE=AE
(3)DE=AC+BE
【知识点】线段垂直平分线的性质;线段垂直平分线的判定
18.【答案】(1)解:因为点 在一次函数 的图象上,
所以,
(2)解:因为正比例函数图象经过点 ,
所以, ,所以, ,
所以,
(3)解:对于 ,令 得, ,
所以,点 的坐标为 ,所以, ,
设点 的坐标为 ,
所以, ,
所以,
当 时, ,所以,点 的坐标为
当 时, ,
所以,点 的坐标为
(4)解:存在,理由如下:
由对称性可知,点 关于 轴对称的点的坐标为
设经过点 、点 的直线关系式为 ,
所以, ,所以 ,
所以,直线关系式为 ,
对于, ,令 ,得 ,
所以,点 .
【知识点】一次函数的图象;待定系数法求一次函数解析式;两一次函数图象相交或平行问题;轴对称的应用-最短距离问题
19.【答案】(1)C
(2)解:如图所示,即为所求
(3)60
(4)线段垂直平分线上的点到线段两个端点距离相等或对应点的连线被对称轴垂直平分,(答案不唯一)
【知识点】垂线的概念;线段垂直平分线的性质;利用轴对称设计图案
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【沪科版八上同步练习】
15.2线段的垂直平分线
一、单选题
1.如图,△ABC中,DE是AC的垂直平分线,AE= 5cm,△ABD的周长为16cm,则△ABC的周长为( )
A.21cm B.26cm C.28cm D.31cm
2.如图,在中,分别以A,B为圆心,大于的长度为半径画弧,两弧相交于点P和点O,作直线交于点E,交于点D,若,,则的周长为( )
A.9 B. C.13 D.18
3.如图,三个小朋友相约周末出去玩,图中点A、B、C代表三人的家所在的位置,为公平起见,集合地应定在以下什么位置,可以使三个小朋友的家到集合地的距离相等?( )
A.在三条高线所在的直线的交点处
B.在三条中线的交点处
C.在三条边的垂直平分线的交点处
D.在三条角平分线的交点处
4.如图,在△ABC中,分别以点A和点C为圆心,大于 AC长为半径画弧,两弧相交于点M,N,作直线MN分别交BC,AC于点D,E.若AE=3cm,△ABD的周长为13cm,则△ABC的周长为( )
A.16cm B.19cm C.22cm D.25cm
5.在 中, , .用无刻度的直尺和圆规在BC边上找一点D,使 为等腰三角形.下列作法错误的是( )
A. B.
C. D.
二、填空题
6.如图,在中,,边的垂直平分线交点D,交于点E,连接.若的周长为12,,则的周长为 .
7.如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,已知△BCE的周长是15,AC比BC长3,则AC长为 .
8.如图,在 中,AB的垂直平分线交A于点D,交BC于点E,若 , ,则 的周长为 .
9.平面直角坐标系中,点 ,当 时, 的值最小.
10.如图,在等腰在△ABC中,AB=27,AB的垂直平分线交AB于点D,交AC于点E,若在△BCE的周长为50,则底边BC的长为 .
11.在 中,边 、 的垂直平分线分别交边 于点 、点 , ,则 °.
三、计算题
12.已知ABC中∠BAC=140°, AB、AC的垂直平分线分别交BC于E、F,AEF的周长为10㎝,求BC的长度和∠EAF的度数.
四、解答题
13.如图,在△ABC中,DE是AC的垂直平分线,AC=10,△ABD的周长为18,求△ABC的周长.
14.如图所示,在△ABC中,∠BAC=105°,若MP和NQ分别垂直平分AB和AC.求∠PAQ的度数.
15.如图,在中,,于点,交于点,,连接.
(1)如图1,当在内部时,求证:;
(2)如图2,当的边,分别在外部和内部时,求证:.
五、综合题
16.如图,在长度为1个单位长度的小正方形组成的正方形网格中, ABC的三个顶点A、B、C都在格点上.
( 1 )在图中画出与 ABC关于直线y成轴对称的 A1B1C1;
( 2 )求 ABC的面积;
( 3 )在x轴上找出一点P,使得PB+PC的值最小.(不需计算,在图上直接标记出点P的位置)
17.如图1,已知△ABC中,AB=AC,点D是△ABC外一点(与点A分别在直线BC两侧).且DB=DC,过点D作DE//AC,交射线AB于E,连接AD交BC于F.
(1)求证:AD垂直BC;
(2)如图1,点E在线段AB上且不与B重合时,求证:DE=AE;
(3)如图2,当点E在线段AB的延长线上时,请直接写出线段DE,AC,BE的数量关系.
18.如图,一次函数 的图象分别与 轴和 轴交于 , 两点,且与正比例函数 的图象交于点 .
(1)求 的值;
(2)求正比例函数的表达式;
(3)点 是一次函数图象上的一点,且 的面积是3,求点 的坐标;
(4)在 轴上是否存在点 ,使 的值最小?若存在,求出点 的坐标,若不存在,说明理由.
六、实践探究题
19.如何设计与制作风筝呢?请同学们阅读“勤学小组”的项目实施过程,帮助他们解决项目实施过程中遇到的问题。
项目主题:设计与制作风筝.
项目实施:
(1)任务一:了解风筝:“勤学小组”的同学查阅了有关风筝的历史,种类,结构,制作等方面的资料,同时还收集到如图的风筝图案,请你帮助他们从中选出不是轴对称图形的风筝图案
(2)任务二:设计风筝:设计风筝时主要进行风筝面与风筝骨架的设计.“勤学小组”的同学设计好了风筝面,接下来在正方形网格中进行风筝骨架的设计,请你帮助他们以直线l为对称轴画出风筝骨架的另一半.
(3)任务三:制作风筝:传统风筝的技艺概括起来四个字:扎、糊、绘、放,简称“四艺”.“勒学小组”的同学准备用竹条扎制如图所示的风筝骨架,已知AD⊥BC于点D, BD=CD,AB=60cm,则竹条AC的长为 cm.
(4)任务四:放飞风筝:同学们拿着自己设计与制作的风筝进行了试飞,并根据试飞结果对风筝进行了修改完善.
项目反思:同学们对项目学习的整个过程进行反思,并编写了“简易风筝制作说明书”。请你写出一条在项目实施的过程中用到的数学知识
答案解析部分
1.【答案】B
【知识点】线段垂直平分线的性质
2.【答案】C
【知识点】线段垂直平分线的性质;尺规作图-垂直平分线
3.【答案】C
【知识点】线段垂直平分线的性质
4.【答案】B
【知识点】线段垂直平分线的性质
5.【答案】A
【知识点】尺规作图-垂直平分线
6.【答案】7
【知识点】线段垂直平分线的性质
7.【答案】9
【知识点】线段垂直平分线的性质
8.【答案】11
【知识点】线段垂直平分线的性质
9.【答案】
【知识点】待定系数法求一次函数解析式;轴对称的应用-最短距离问题
10.【答案】23
【知识点】线段垂直平分线的性质
11.【答案】80或100
【知识点】三角形内角和定理;线段垂直平分线的性质
12.【答案】解:∵AB、AC的垂直平分线分别交BC于E、F,
∴AE=BE,AF=CF;
∵△AEF周长为:AE+EF+AF=BE+EF+CF=BC=10㎝,
∴BC=10㎝,
又∵AB、AC的垂直平分线分别交BC于E、F,
∴AE=BE,AF=CF,
∴∠B=∠BAE,∠C=∠CAF,
∵△ABC中,∠BAC=140°,
∴∠B+∠C=180°-∠BAC=40°,
∴∠BAE+∠CAF=40°,
∴∠EAF=∠BAC-(∠BAE+∠CAF)=140°-40°=100°。
【知识点】三角形内角和定理;线段垂直平分线的性质
13.【答案】解:∵DE是AC的垂直平分线,
∴AD=CD,
∵△ABD得周长为18,
∴AB+BD+AD=18,
∴AB+BD+CD=AB+BC=18,
∴△ABC得周长为AB+BC+AC=28.
【知识点】线段垂直平分线的性质
14.【答案】解:∵MP为AB的垂直平分线,
∴PA=PB,
∴∠B=∠PAB,
同理∠C=∠QAC,
∴∠B+∠C=∠PAB+∠QAC,
∵∠B+∠C=180°-∠BAC=180°-105°=75°,
∴∠PAB+∠QAC=75°,
∴∠PAQ=∠BAC-(∠PAB+∠QAC)
=105°-75°
=30°.
【知识点】三角形内角和定理;线段垂直平分线的性质
15.【答案】(1)证明:如图,在上截取,连接.
∵,
∴,.
又∵,
∴.
∵,
∴.
∴.
∴.
在和中,
∴.
∴.
∴.
(2)证明:如图,在的延长线上截取,连接.
∵,
∴,.
又∵,
∴.
∵,
∴.
∴.
∴.
在和中,
∴.
∴.
∵,
∴.
【知识点】三角形全等及其性质;线段垂直平分线的性质;三角形全等的判定-SAS;线段的和、差、倍、分的简单计算
16.【答案】解:(1)如图所示,△A1B1C1即为所求;
(2)△ABC的面积=3×3﹣ ×2×3﹣ ×1×2﹣ ×1×3= ;
(3)如图所示,点P即为所求.
【知识点】三角形的面积;作图﹣轴对称;轴对称的应用-最短距离问题
17.【答案】(1)证明:∵AB=AC
∴点A在线段BC的垂直平分线上,
∵DB=DC
∴点D在线段BC的垂直平分线上,
∴直线AD是BC的垂直平分线,
∴AD垂直BC;
(2)解:∵AB=AC,AD⊥BC
∴∠BAD=∠CAD
∵DE∥AC
∴∠EDA=∠CAD
∴∠BAD=∠EDA
∴DE=AE
(3)DE=AC+BE
【知识点】线段垂直平分线的性质;线段垂直平分线的判定
18.【答案】(1)解:因为点 在一次函数 的图象上,
所以,
(2)解:因为正比例函数图象经过点 ,
所以, ,所以, ,
所以,
(3)解:对于 ,令 得, ,
所以,点 的坐标为 ,所以, ,
设点 的坐标为 ,
所以, ,
所以,
当 时, ,所以,点 的坐标为
当 时, ,
所以,点 的坐标为
(4)解:存在,理由如下:
由对称性可知,点 关于 轴对称的点的坐标为
设经过点 、点 的直线关系式为 ,
所以, ,所以 ,
所以,直线关系式为 ,
对于, ,令 ,得 ,
所以,点 .
【知识点】一次函数的图象;待定系数法求一次函数解析式;两一次函数图象相交或平行问题;轴对称的应用-最短距离问题
19.【答案】(1)C
(2)解:如图所示,即为所求
(3)60
(4)线段垂直平分线上的点到线段两个端点距离相等或对应点的连线被对称轴垂直平分,(答案不唯一)
【知识点】垂线的概念;线段垂直平分线的性质;利用轴对称设计图案
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
